Finding the Equation of the Tangent Line to






















- Slides: 36

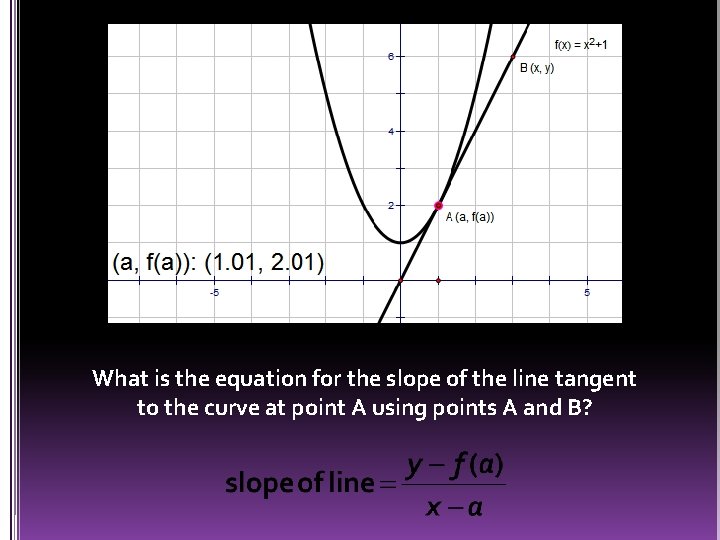
Finding the Equation of the Tangent Line to a Curve Remember: Derivative=Slope of the Tangent Line




What is the equation for the slope of the line tangent to the curve at point A using points A and B?

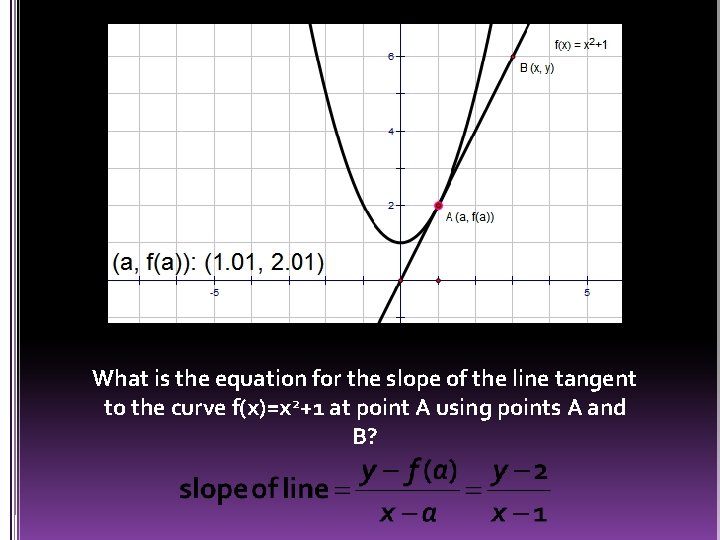
What is the equation for the slope of the line tangent to the curve f(x)=x 2+1 at point A using points A and B?

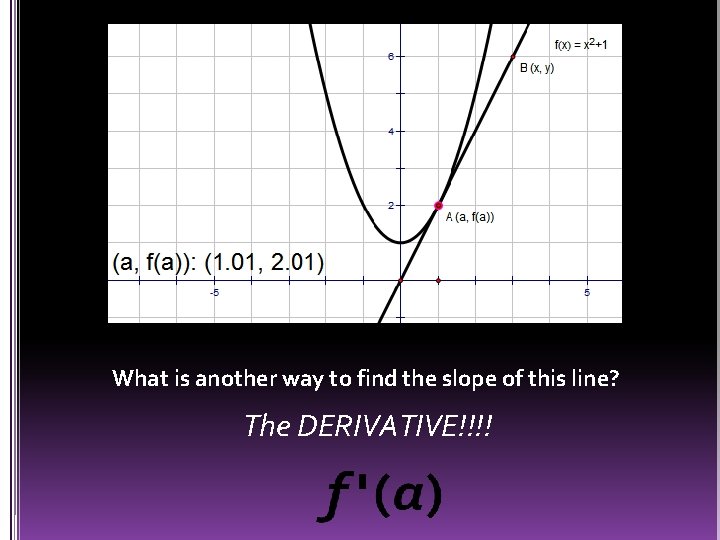
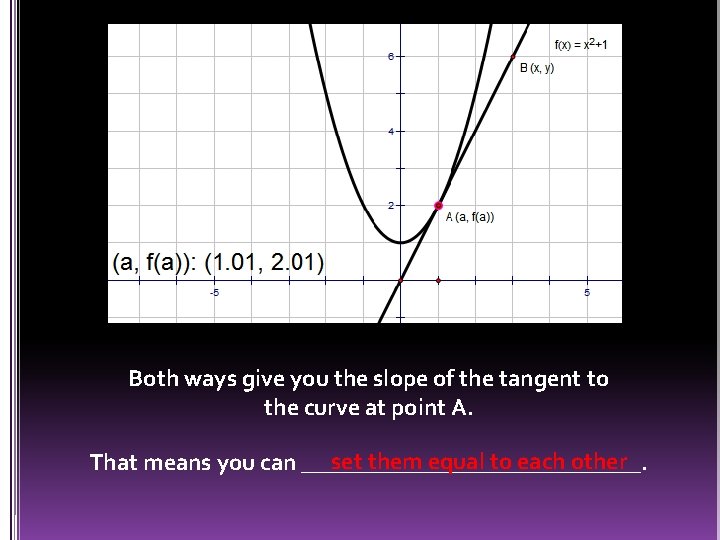
What is another way to find the slope of this line? The DERIVATIVE!!!!

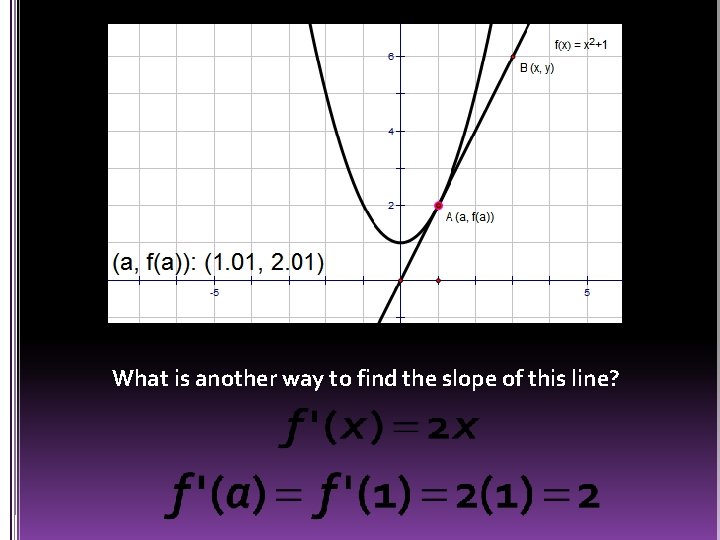
What is another way to find the slope of this line?

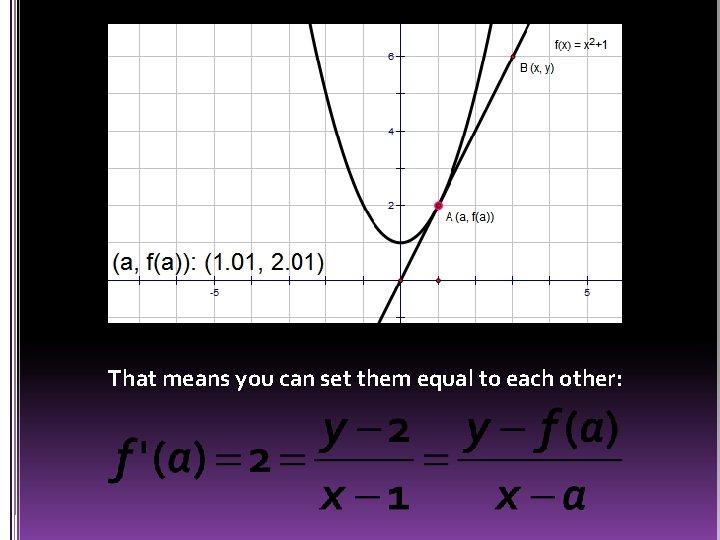
Both ways give you the slope of the tangent to the curve at point A. set them equal to each other That means you can _______________.

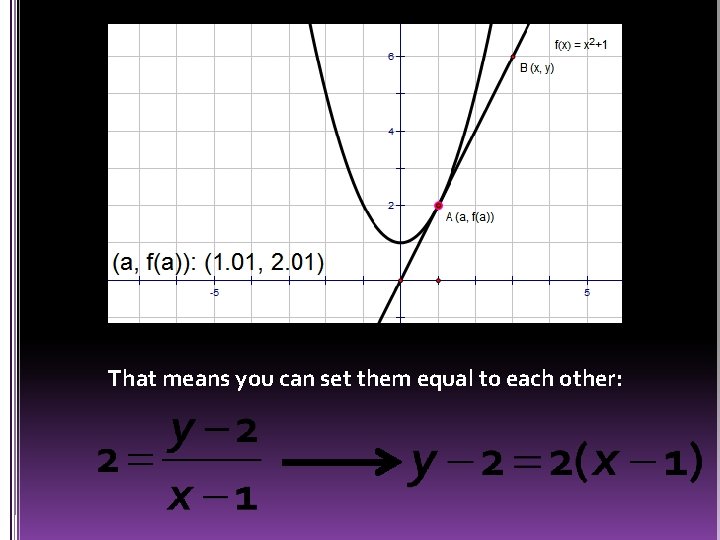
That means you can set them equal to each other:

That means you can set them equal to each other:

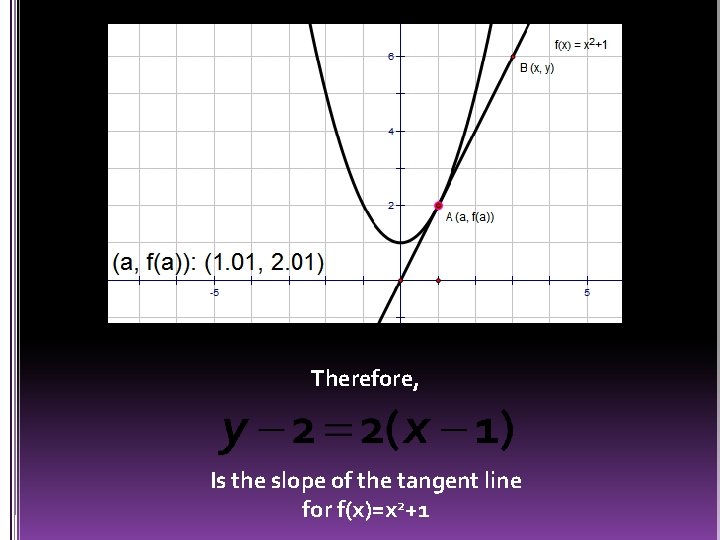
Therefore, Is the slope of the tangent line for f(x)=x 2+1

Formula of the tangent line at a point A (a, f(a)) y-f(a)=f’(a)(x-a)

Step 1: Find the point of contact by plugging in the x-value in f(x). This is f(a).

Step 2: Find f’(x). Plug in x-value for f’(a)

Step 3: Plug all known values into formula y-f(a)=f’(a)(x-a)

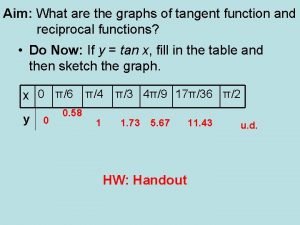
Find the equation of the tangent to y=x 3+2 x at: l x=2 l x=-1 l x=-2

Question: If the tangent line to a point of f(x) was horizontal, what would that tell us about f’(x)? f’(x)=0

Step 1: Find the derivative, f’(x)

Step 2: Set derivative equal to zero and solve, f’(x)=0

Step 3: Plug solutions into original formula to find y-value, (solution, yvalue) is the coordinates.

Note: If it asks for the equation then you will write y=y value found when you plugged in the solutions for f’(x)=0



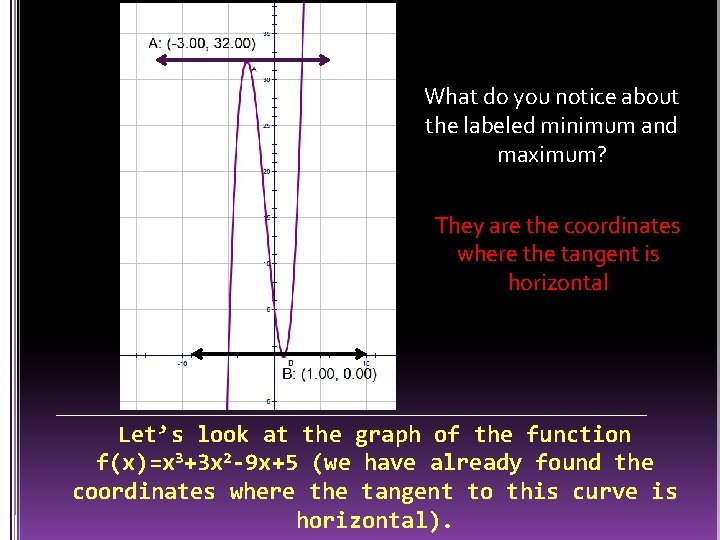
What do you notice about the labeled minimum and maximum? They are the coordinates where the tangent is horizontal Let’s look at the graph of the function f(x)=x 3+3 x 2 -9 x+5 (we have already found the coordinates where the tangent to this curve is horizontal).

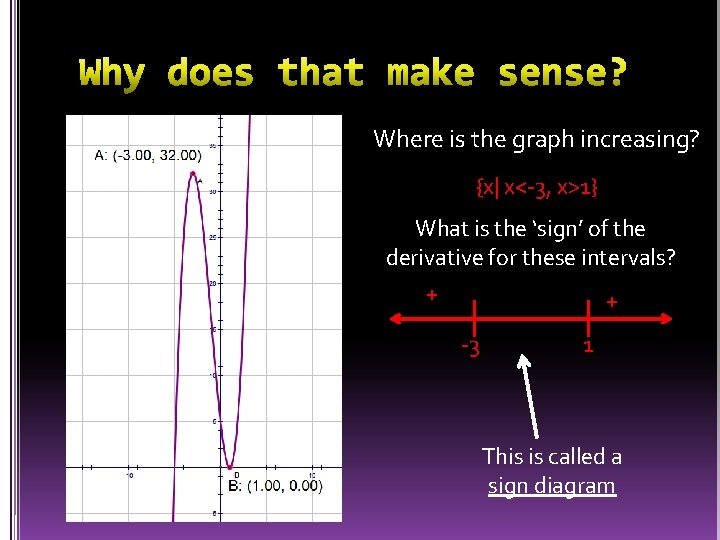
Where is the graph increasing? {x| x<-3, x>1} What is the ‘sign’ of the derivative for these intervals? + + -3 1 This is called a sign diagram

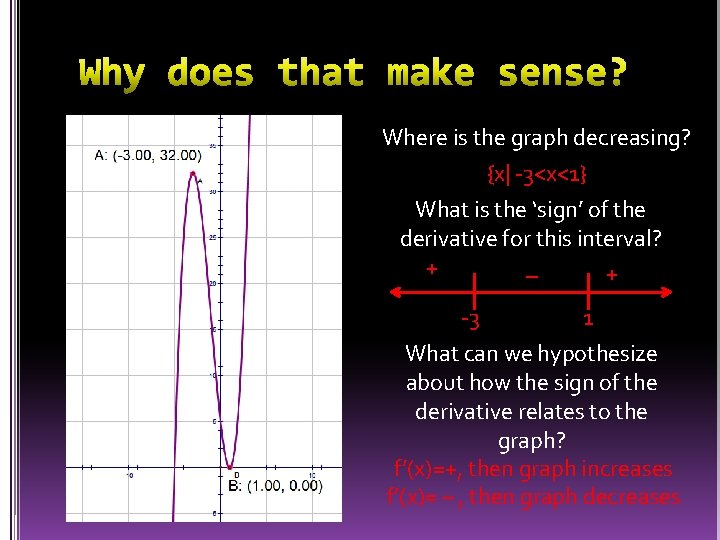
Where is the graph decreasing? {x| -3<x<1} What is the ‘sign’ of the derivative for this interval? + + – -3 1 What can we hypothesize about how the sign of the derivative relates to the graph? f’(x)=+, then graph increases f’(x)= – , then graph decreases

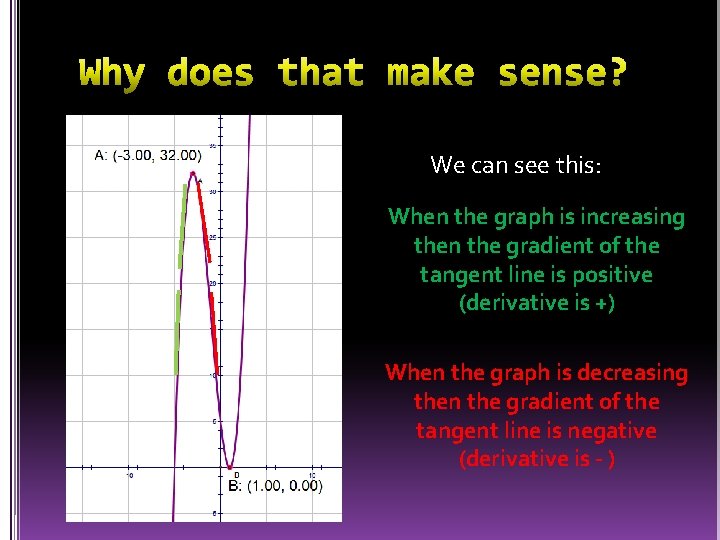
We can see this: When the graph is increasing then the gradient of the tangent line is positive (derivative is +) When the graph is decreasing then the gradient of the tangent line is negative (derivative is - )


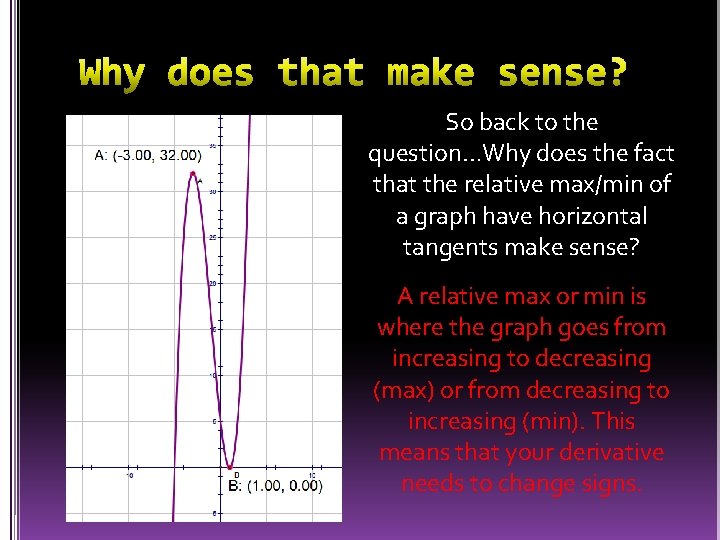
So back to the question…Why does the fact that the relative max/min of a graph have horizontal tangents make sense? A relative max or min is where the graph goes from increasing to decreasing (max) or from decreasing to increasing (min). This means that your derivative needs to change signs.

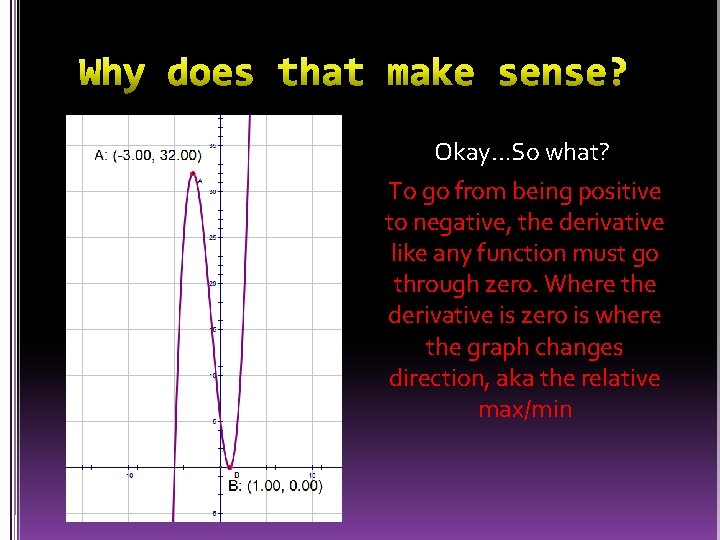
Okay…So what? To go from being positive to negative, the derivative like any function must go through zero. Where the derivative is zero is where the graph changes direction, aka the relative max/min

Take a look at f(x)=x 3. What is the coordinates of the point on the function where the derivative is equal to 0? Find the graph in your calculator, is this coordinate a relative maximum or a relative minimum? NO – the graph only flattened out then continued in the same direction This is called a HORIZONTAL INFLECTION

It is necessary to make a sign diagram to determine whether the coordinate where f’(x)=0 is a relative maximum, minimum, or a horizontal inflection.

Anywhere that f’(x)=0 is called a stationary point; a stationary point could be a relative minimum, a relative maximum, or a horizontal inflection

What do you know about the graph of f(x) when f’(x) is a) Positive b) Negative c) Zero What do you know about the slope of the tangent line at a relative extrema? Why is this so? Sketch a graph of f(x) when the sign diagram of f’(x) looks like – + -5 – 1 What are the types of stationary points? What do they all have in common? What do the sign ? diagrams for each type look like? ? Stationary Point

 Internal tangent vs external tangent
Internal tangent vs external tangent 9.6 secants, tangents, and angle measures answers
9.6 secants, tangents, and angle measures answers Tangent formula
Tangent formula Equation of a tangent line
Equation of a tangent line Tangent function graph
Tangent function graph Tangent period
Tangent period Persamaan garis yang menyinggung kurva y=2x3-4x+3
Persamaan garis yang menyinggung kurva y=2x3-4x+3 X^1/2 times x^1/2
X^1/2 times x^1/2 Derivative of a function to the slope of the tangent line
Derivative of a function to the slope of the tangent line Higher maths circles
Higher maths circles External tangents of two circles
External tangents of two circles Vertical tangent line
Vertical tangent line Normal line definition
Normal line definition Line that is tangent to two coplanar circles
Line that is tangent to two coplanar circles Tangentline nspire
Tangentline nspire Tangent line approximation
Tangent line approximation Tangent line怎么求
Tangent line怎么求 The tangent line problem
The tangent line problem Differentiate between plain scale and diagonal scale
Differentiate between plain scale and diagonal scale Vertex formula quadratic function
Vertex formula quadratic function Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worm breton
Tư thế worm breton Hát lên người ơi alleluia
Hát lên người ơi alleluia Môn thể thao bắt đầu bằng chữ f
Môn thể thao bắt đầu bằng chữ f Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống