Section 4 3 The Derivative in Graphing and

All graphics are attributed to: • Calculus, 10/E by Howard Anton, Irl Bivens, and

Introduction • In this section we will discuss procedures for graphing rational functions and

Graphing Rational Functions • Recall that a rational function is a function in the

Example with Oblique or Curvilinear Asymptotes • There are examples on the bottom half

Graphs with Vertical Tangents and Cusps • We commonly find points in our graphs

Example with Vertical Tangents • Follow the same steps as the previous example, but

Example with Vertical Tangents con’t • Step 6 (this is where the extra work

Example with Vertical Tangents con’t • Steps 4 & 7

Slides: 14

Download presentation

Section 4. 3 The Derivative in Graphing and Applications- “Analysis of Functions III: Rational Functions, Cusps, and Vertical Tangents”

Introduction • In this section we will discuss procedures for graphing rational functions and other kinds of curves. • In many problems, the “properties of interest” in the graph of a function are: symmetries x-intercepts relative extrema intervals of increasing and decreasing asymptotes periodicity y-intercepts concavity inflection points end behavior • Some of these properties may not be relevant in certain cases; for example, polynomials do not have asymptotes.

Graphing Rational Functions • Recall that a rational function is a function in the form f(x) = P(x)/Q(x) which is the ratio of polynomials P(x) and Q(x). • Before graphing, check to make sure whether or not P(x) and Q(x) have any common factors. If they do, there will be holes in the graph. • After that, you will be looking at many of the properties listed on the previous slide. • You will find more specific instructions on the next slide.

Example – Steps 1 -3

Example continued – Steps 4 -7

Example with Oblique or Curvilinear Asymptotes • There are examples on the bottom half of page 258 where the rational functions have a higher degree polynomial in the numerator than in the denominator. • These result in other kinds of asymptotes, such as slant (oblique) asymptotes or curvilinear asymptotes. • We will not do these this year.

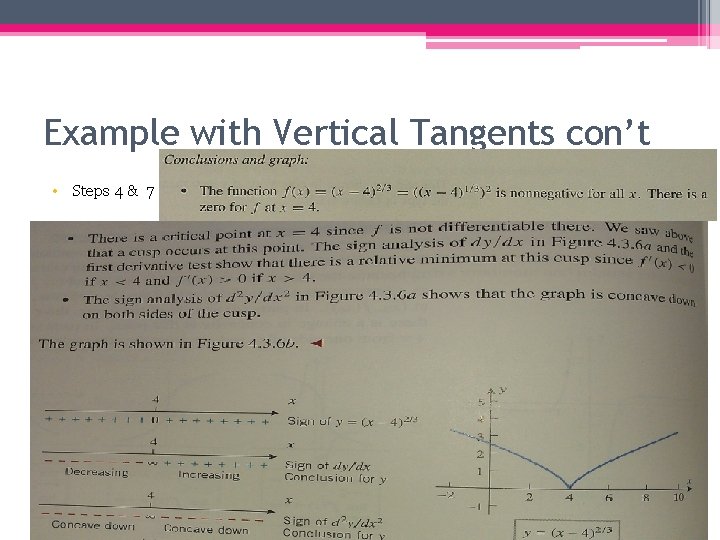
Graphs with Vertical Tangents and Cusps • We commonly find points in our graphs where there is a vertical tangent line, therefore, the function is not differentiable at those values of x. • There are four examples of this occurring on the next slide. • In the first two graphs, a&b, there is an inflection point with the vertical tangent line. • In the second two graphs, c&d, there is a cusp (where the limit approaching from the left does not equal the limit approaching from the right).