10 1 Tangents to Circles A circle is



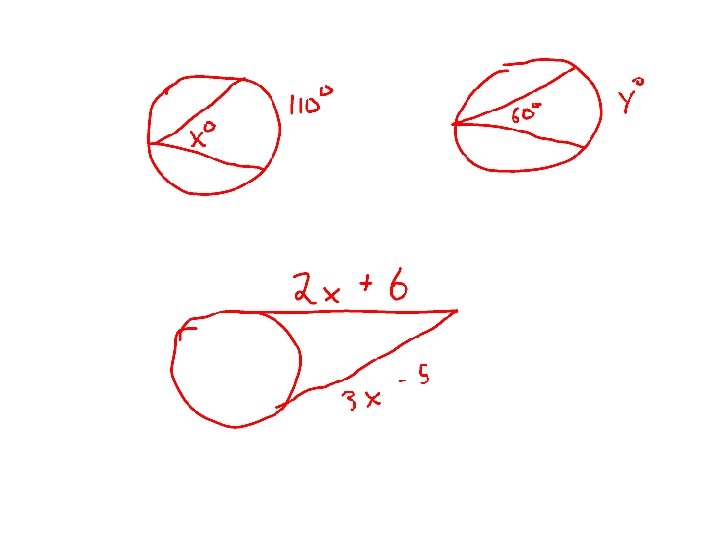


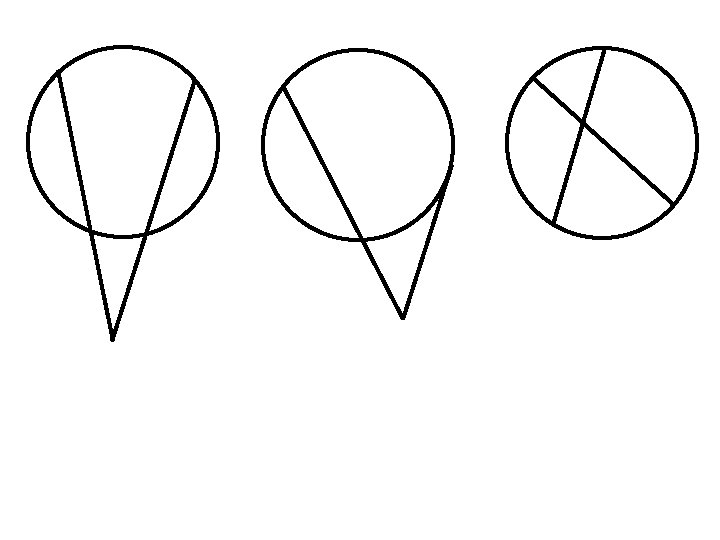


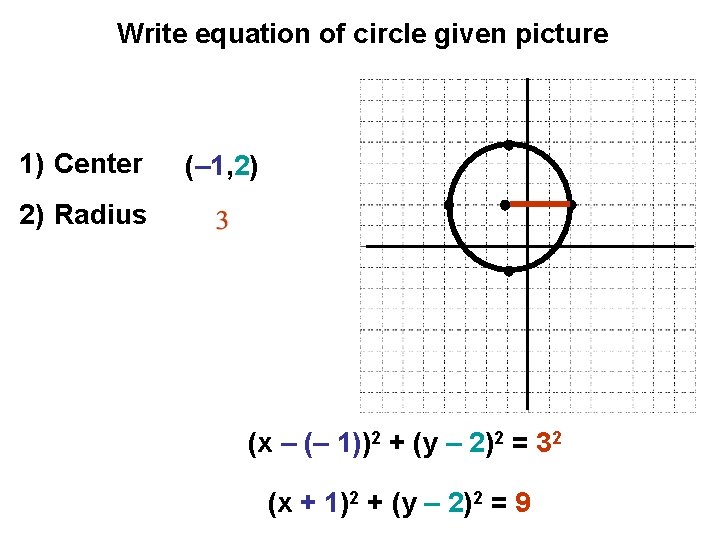



- Slides: 45

10. 1 – Tangents to Circles

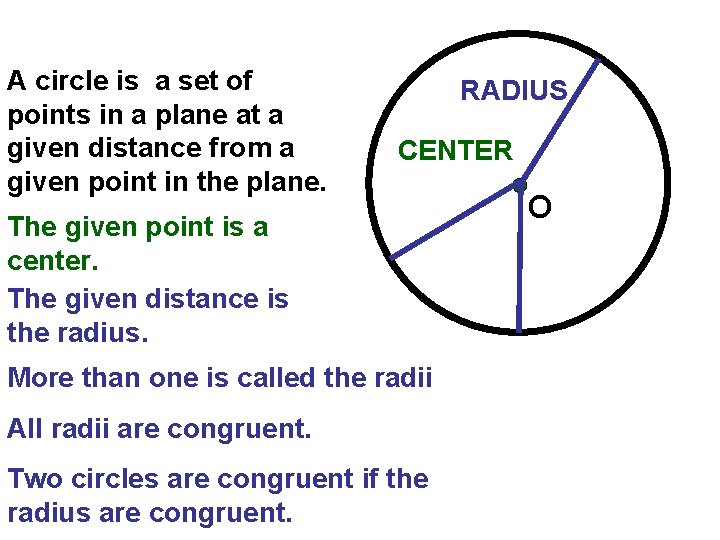
A circle is a set of points in a plane at a given distance from a given point in the plane. RADIUS CENTER The given point is a center. The given distance is the radius. More than one is called the radii All radii are congruent. Two circles are congruent if the radius are congruent. O

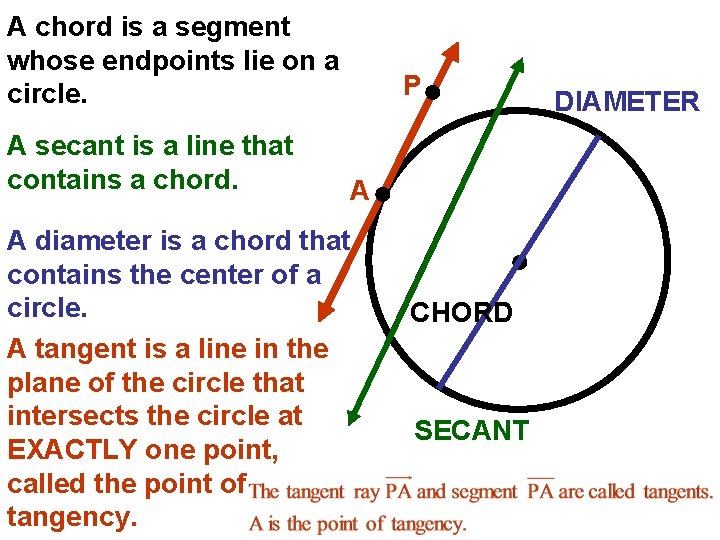
A chord is a segment whose endpoints lie on a circle. A secant is a line that contains a chord. P A A diameter is a chord that contains the center of a circle. A tangent is a line in the plane of the circle that intersects the circle at EXACTLY one point, called the point of tangency. CHORD SECANT DIAMETER

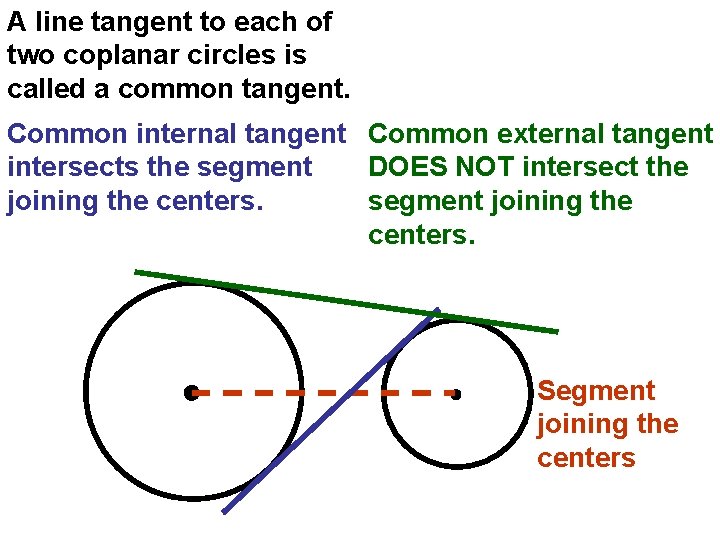
A line tangent to each of two coplanar circles is called a common tangent. Common internal tangent Common external tangent intersects the segment DOES NOT intersect the joining the centers. segment joining the centers. Segment joining the centers

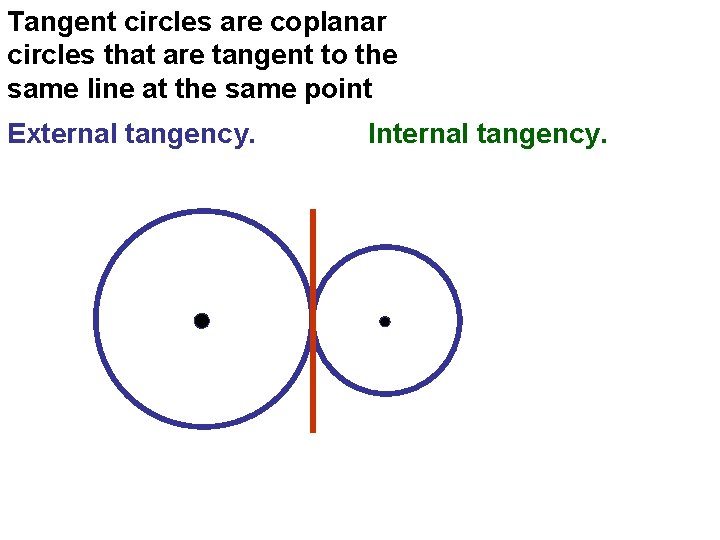
Tangent circles are coplanar circles that are tangent to the same line at the same point External tangency. Internal tangency.

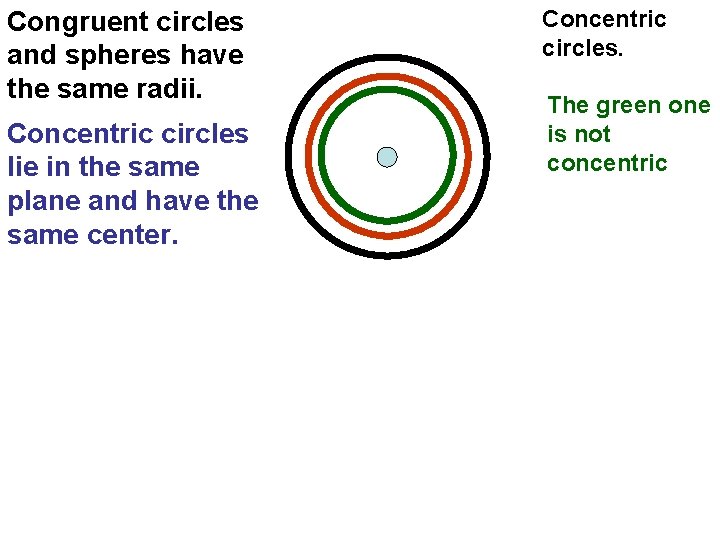
Congruent circles and spheres have the same radii. Concentric circles lie in the same plane and have the same center. Concentric circles. The green one is not concentric

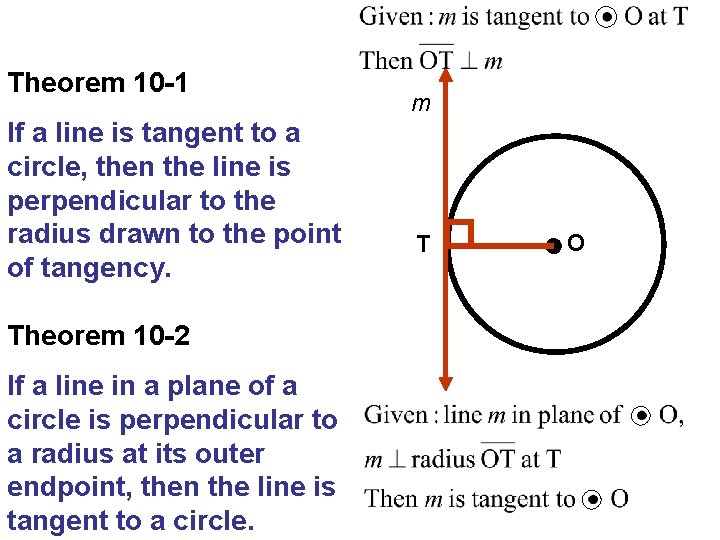
Theorem 10 -1 If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency. Theorem 10 -2 If a line in a plane of a circle is perpendicular to a radius at its outer endpoint, then the line is tangent to a circle. m T O

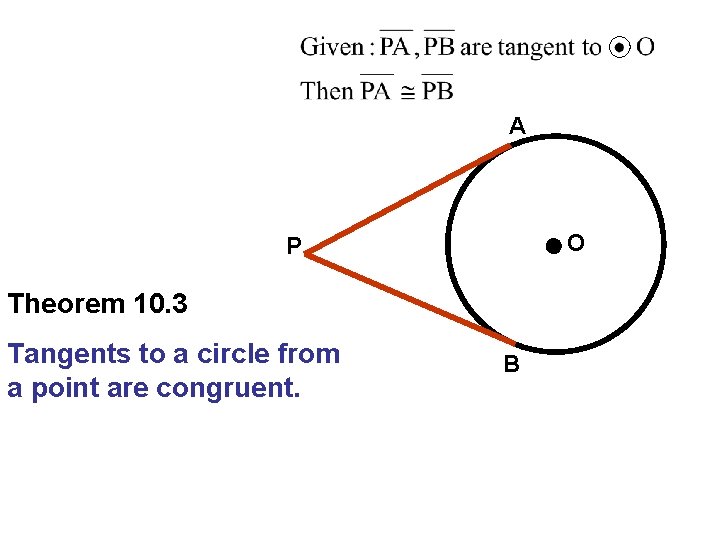
A O P Theorem 10. 3 Tangents to a circle from a point are congruent. B

A O P B

10. 2 – Arcs and Chords

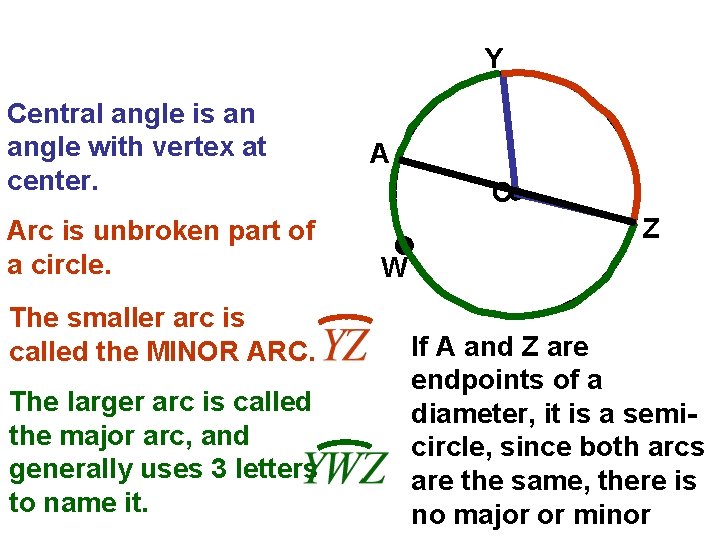
Y Central angle is an angle with vertex at center. Arc is unbroken part of a circle. The smaller arc is called the MINOR ARC. The larger arc is called the major arc, and generally uses 3 letters to name it. A O Z W If A and Z are endpoints of a diameter, it is a semicircle, since both arcs are the same, there is no major or minor

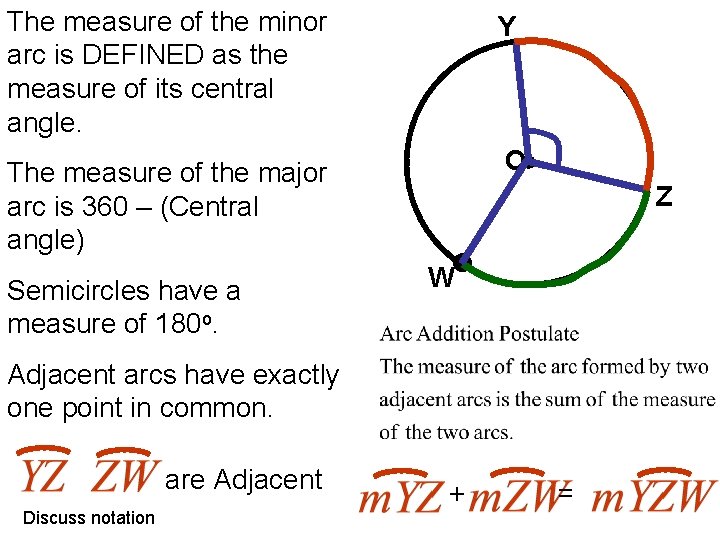
The measure of the minor arc is DEFINED as the measure of its central angle. Y The measure of the major arc is 360 – (Central angle) O Semicircles have a measure of 180 o. Z W Adjacent arcs have exactly one point in common. are Adjacent Discuss notation + =

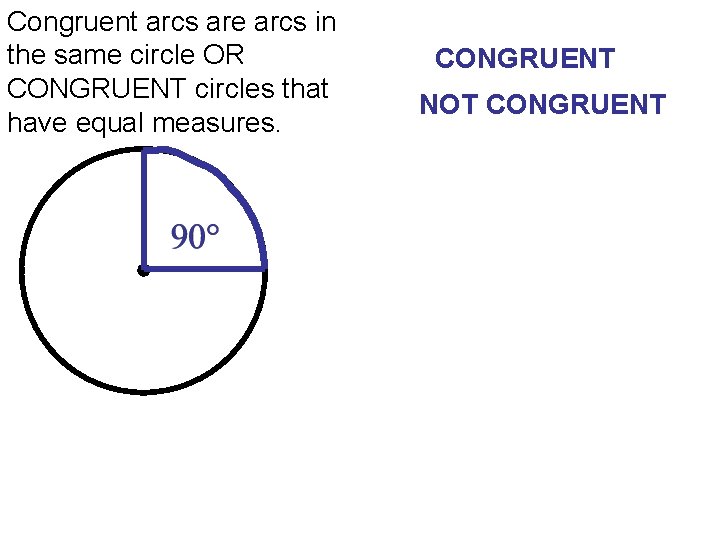
Congruent arcs are arcs in the same circle OR CONGRUENT circles that have equal measures. CONGRUENT NOT CONGRUENT

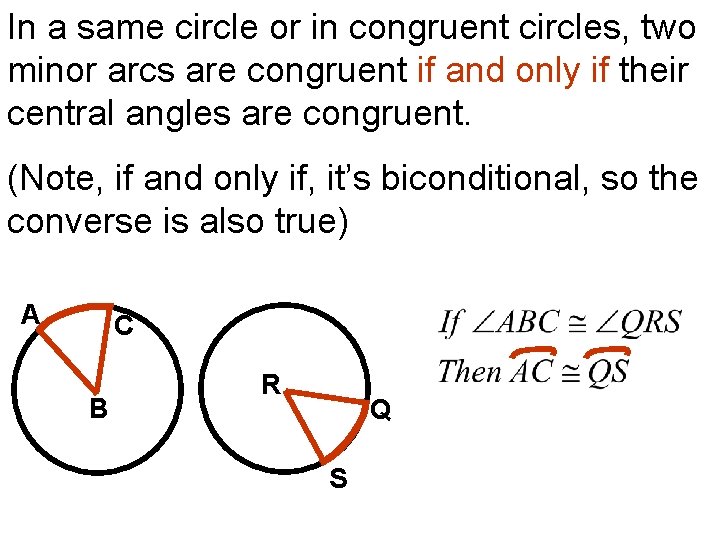
In a same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. (Note, if and only if, it’s biconditional, so the converse is also true) A C B R Q S

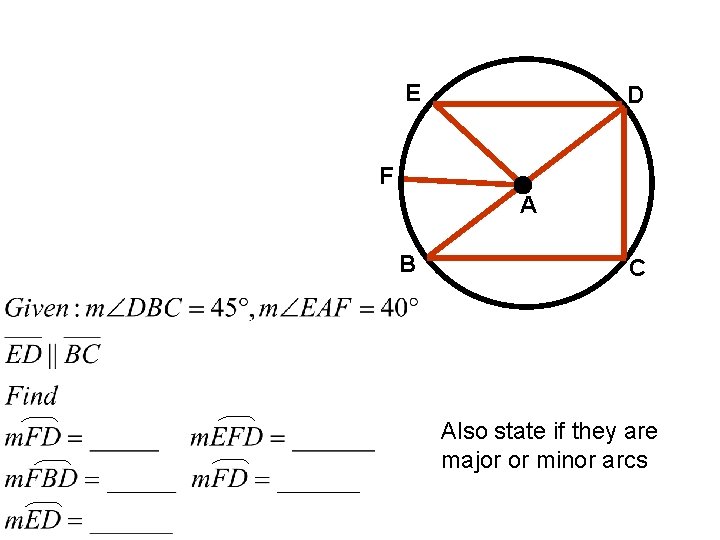
E D F A B C Also state if they are major or minor arcs

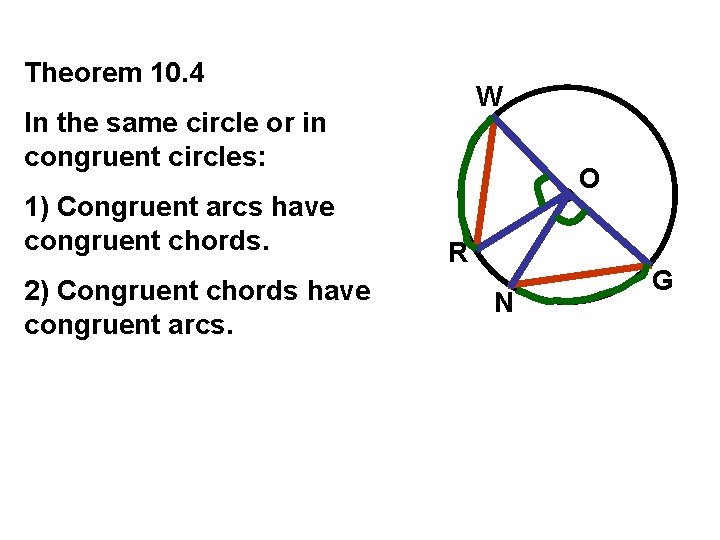
Theorem 10. 4 W In the same circle or in congruent circles: 1) Congruent arcs have congruent chords. 2) Congruent chords have congruent arcs. O R N G

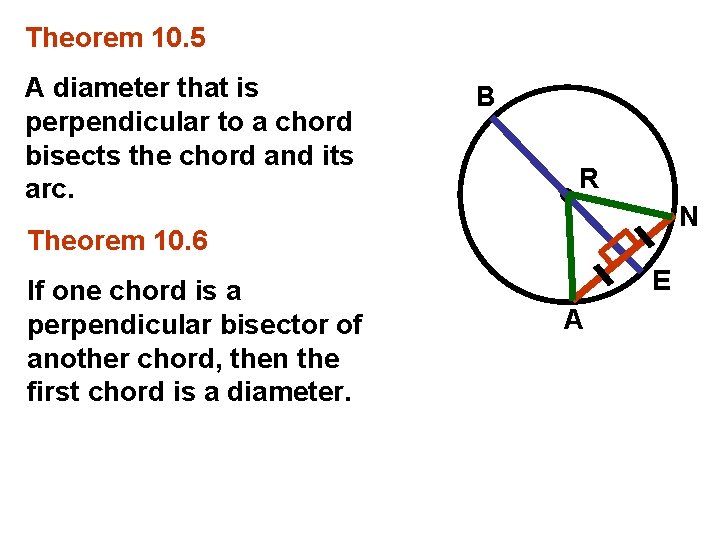
Theorem 10. 5 A diameter that is perpendicular to a chord bisects the chord and its arc. B R N Theorem 10. 6 If one chord is a perpendicular bisector of another chord, then the first chord is a diameter. E A

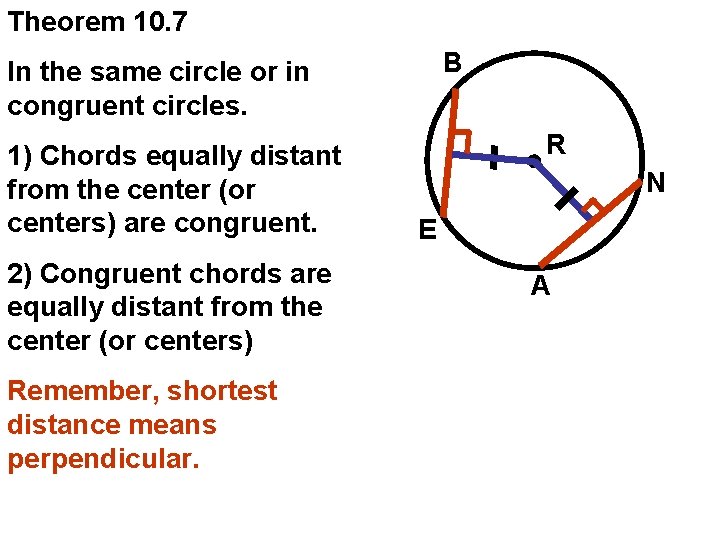
Theorem 10. 7 B In the same circle or in congruent circles. 1) Chords equally distant from the center (or centers) are congruent. 2) Congruent chords are equally distant from the center (or centers) Remember, shortest distance means perpendicular. R N E A

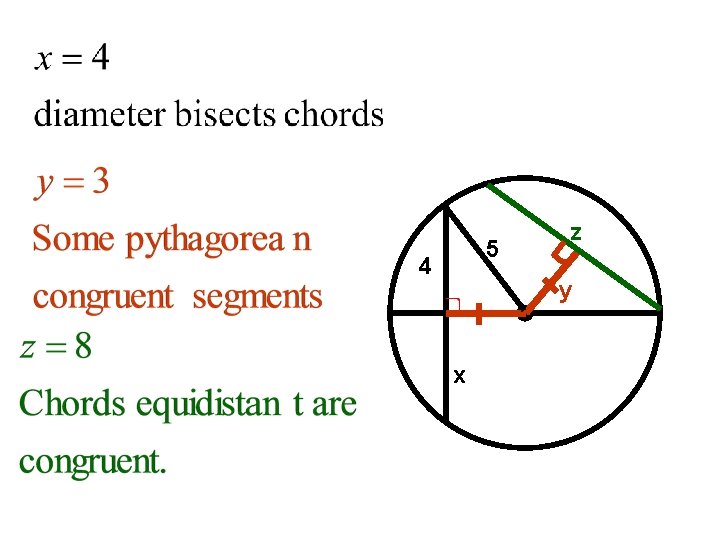
5 4 z y x


10. 3 – Inscribed Angles

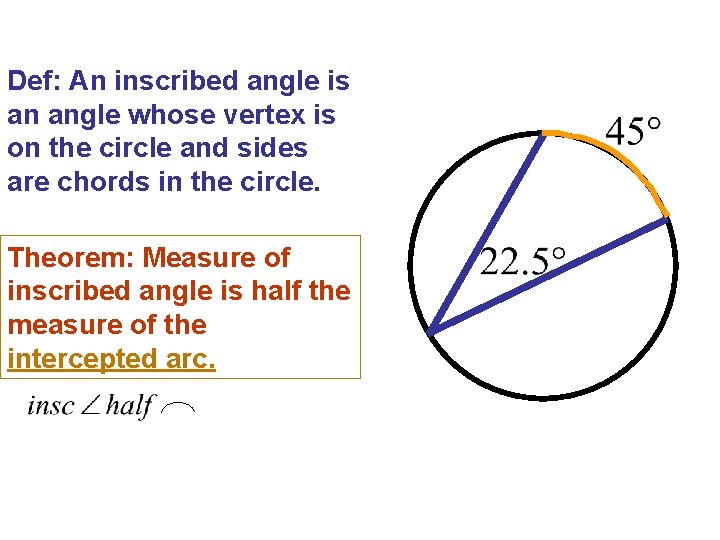
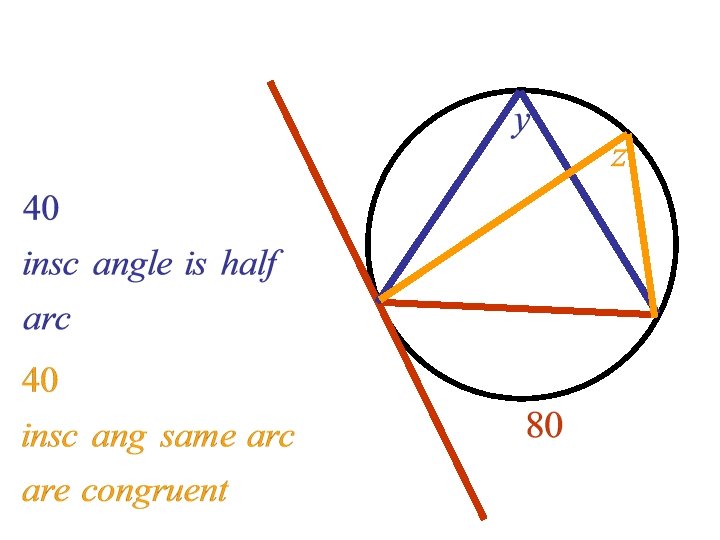
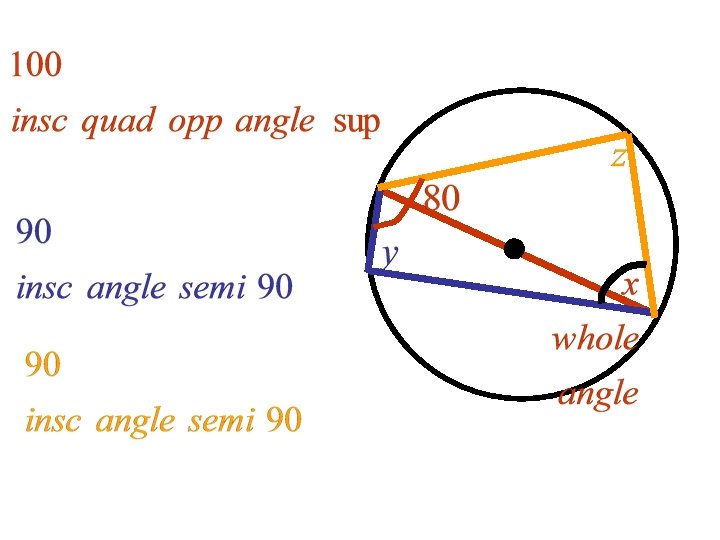
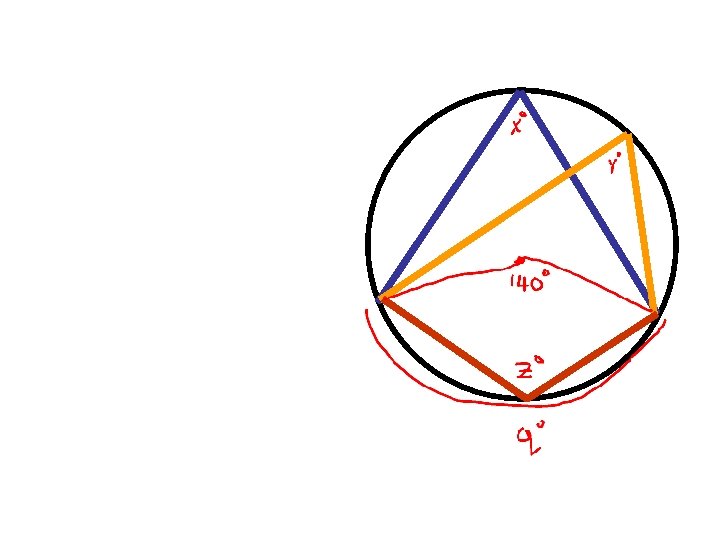
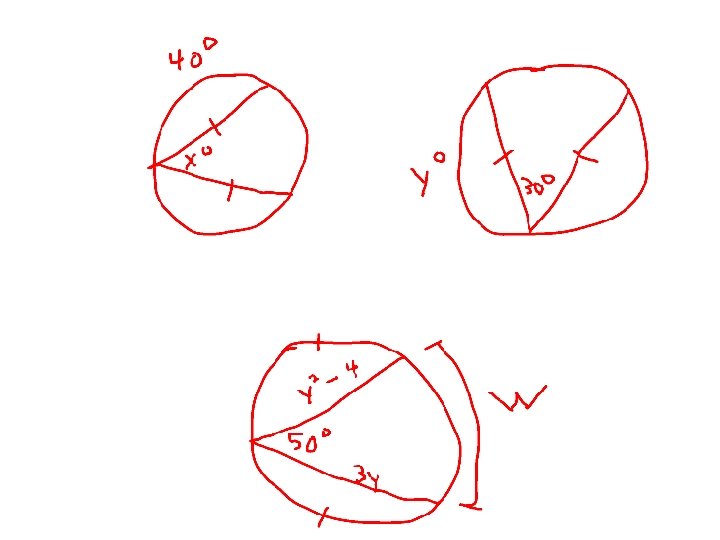
Def: An inscribed angle is an angle whose vertex is on the circle and sides are chords in the circle. Theorem: Measure of inscribed angle is half the measure of the intercepted arc.

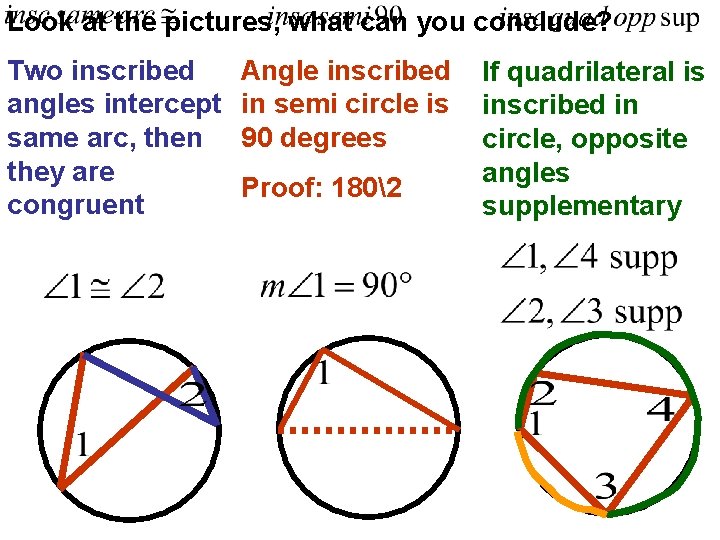
Look at the pictures, what can you conclude? Two inscribed angles intercept same arc, then they are congruent Angle inscribed in semi circle is 90 degrees Proof: 1802 If quadrilateral is inscribed in circle, opposite angles supplementary



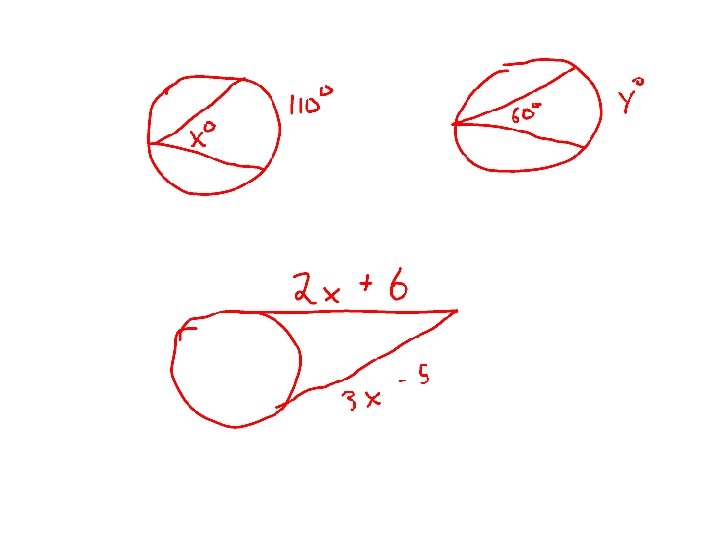



10. 5 – Segment Lengths in Circles

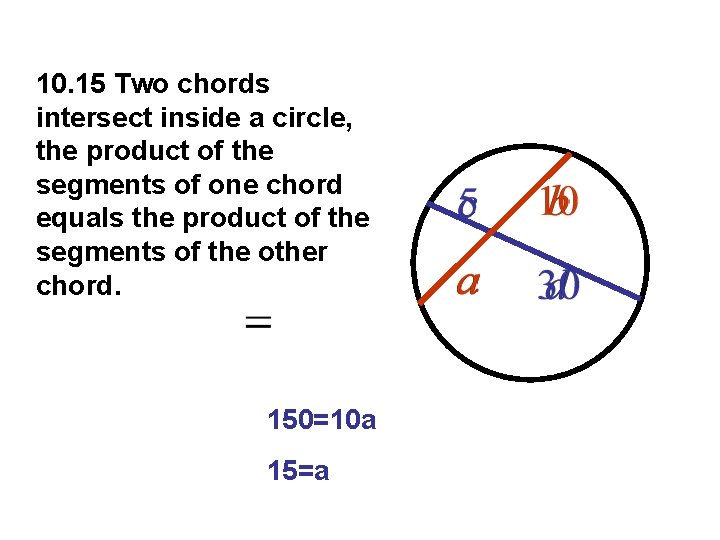
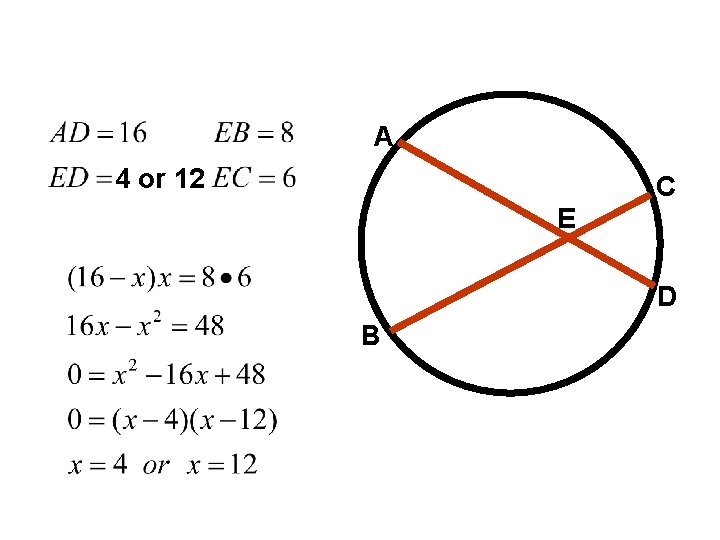
10. 15 Two chords intersect inside a circle, the product of the segments of one chord equals the product of the segments of the other chord. 150=10 a 15=a

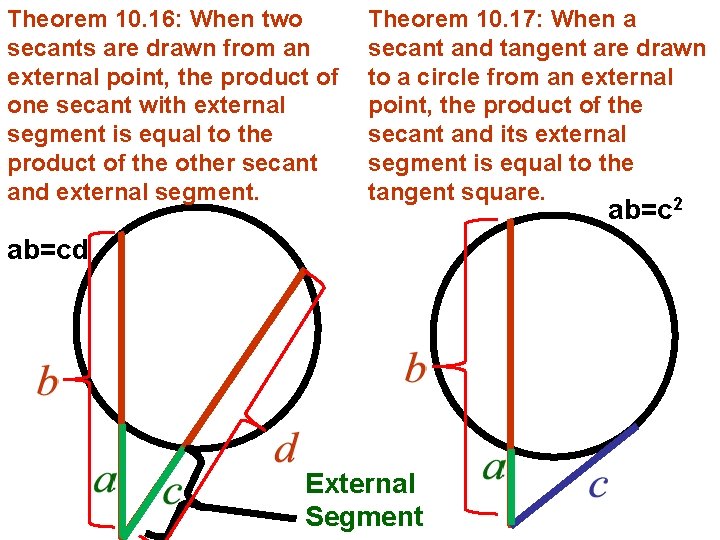
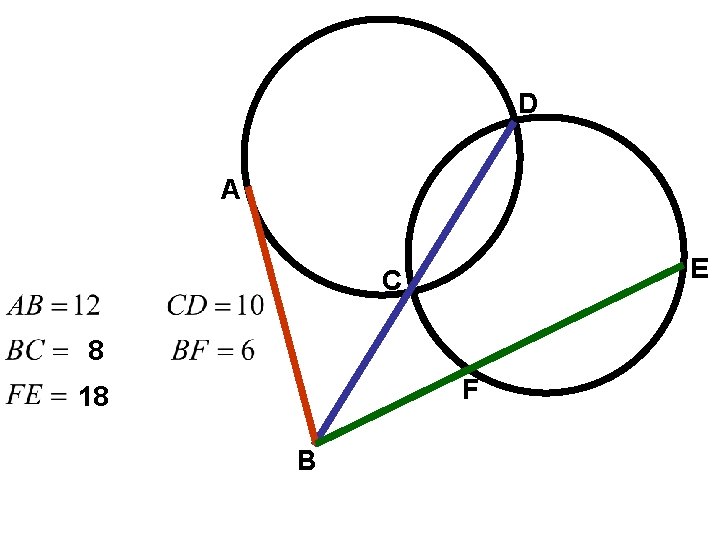
Theorem 10. 16: When two secants are drawn from an external point, the product of one secant with external segment is equal to the product of the other secant and external segment. Theorem 10. 17: When a secant and tangent are drawn to a circle from an external point, the product of the secant and its external segment is equal to the tangent square. 2 ab=cd External Segment ab=c

D A E C 8 F 18 B

A 4 or 12 C E D B


10. 6 – Equations of Circles

Equation of a circle (x – h)2 + (y – k)2 = r 2 (h, k) is the center r is the radius

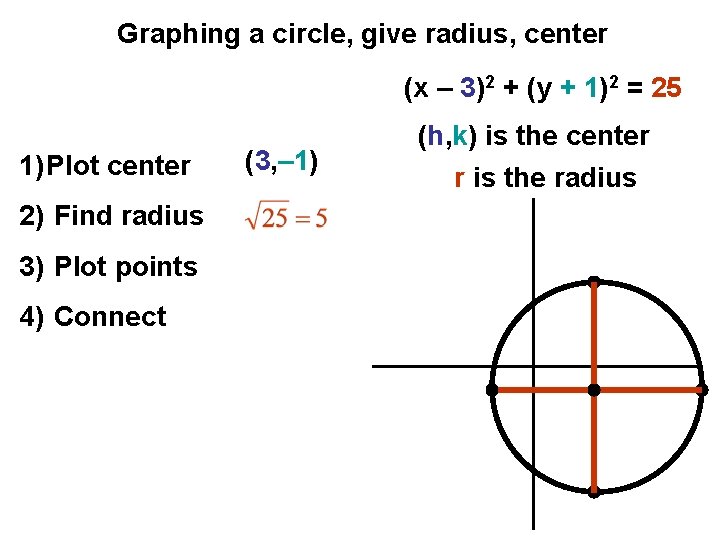
Graphing a circle, give radius, center (x – 3)2 + (y + 1)2 = 25 1) Plot center 2) Find radius 3) Plot points 4) Connect (3, – 1) (h, k) is the center r is the radius

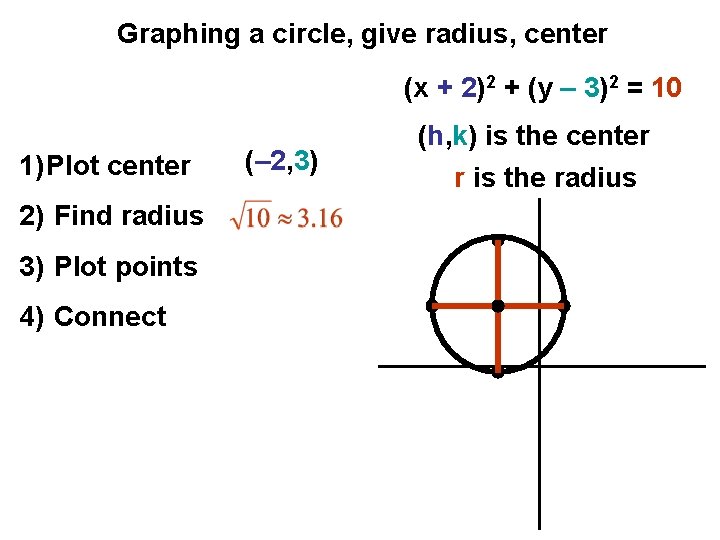
Graphing a circle, give radius, center (x + 2)2 + (y – 3)2 = 10 1) Plot center 2) Find radius 3) Plot points 4) Connect (– 2, 3) (h, k) is the center r is the radius

Write equation given center and radius 1) Center (2, – 4) 2) Radius 1) Center (– 1, 2) 2) Radius (x – 2)2 + (y –(– 4))2 =( )2 (x – (– 1))2 + (y – 2)2 = 32 (x – 2)2 + (y + 4)2 = 21 (x + 1)2 + (y – 2)2 = 9
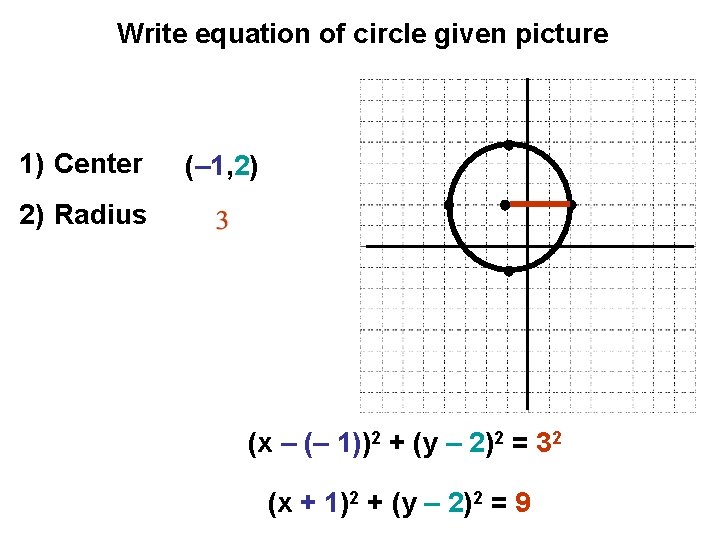
Write equation of circle given picture 1) Center (– 1, 2) 2) Radius (x – (– 1))2 + (y – 2)2 = 32 (x + 1)2 + (y – 2)2 = 9

Write equation given center and point on circle. Center (1, – 3) 1) Use distance formula to find radius 2) Then same as before. Point on Circle ( – 4 , 2)

• In Circle, On circle, Outside Circle • Locus – Circles, lines, and triangles, and basic shapes

Describe the set of points 2 cm from point A Describe the set of points 1 cm from line l Describe the set of points equidistant from points A and B Describe the set of points equidistant to the sides and in the interior of the angle All the points equidistant from points A, B, and C