The Tangent Ratio The Tangent using Angle The

































- Slides: 58

The Tangent Ratio The Tangent using Angle The Tangent Ratio in Action The Tangent (The Adjacent side) The Tangent (Finding Angle) The Sine of an Angle The Sine Ration In Action The Sine ( Finding the Hypotenuse) The Cosine of an Angle Mixed Problems

Angles & Triangles Learning Intention 1. To identify the hypotenuse, opposite and adjacent sides in a right angled triangle. Success Criteria 1. Understand the terms hypotenuse, opposite and adjacent in right angled triangle. 2. Work out Tan Ratio.

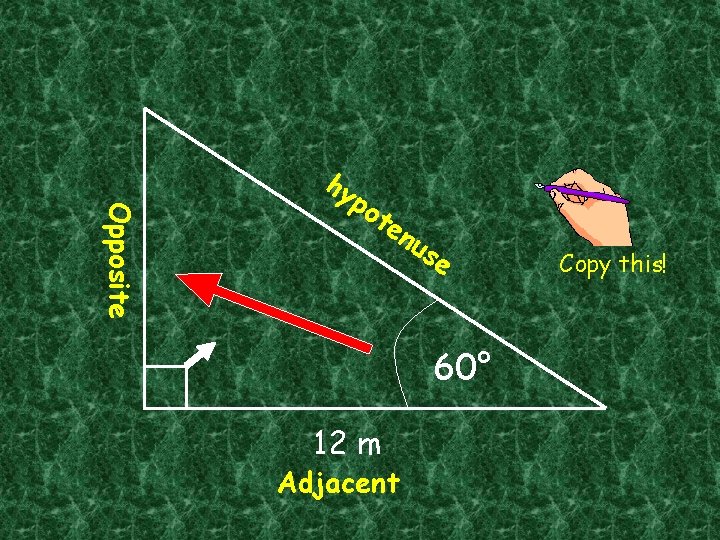
Trigonometry means “triangle” and “measurement”. We will be using right-angled triangles. Opposite hy po t en us e x° Adjacent

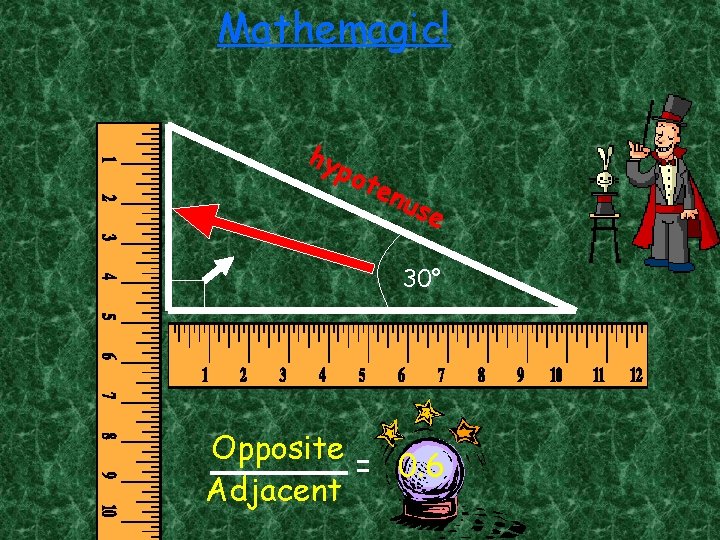
Mathemagic! Opposite hy pot e nus e 30° Adjacent Opposite = 0. 6 Adjacent

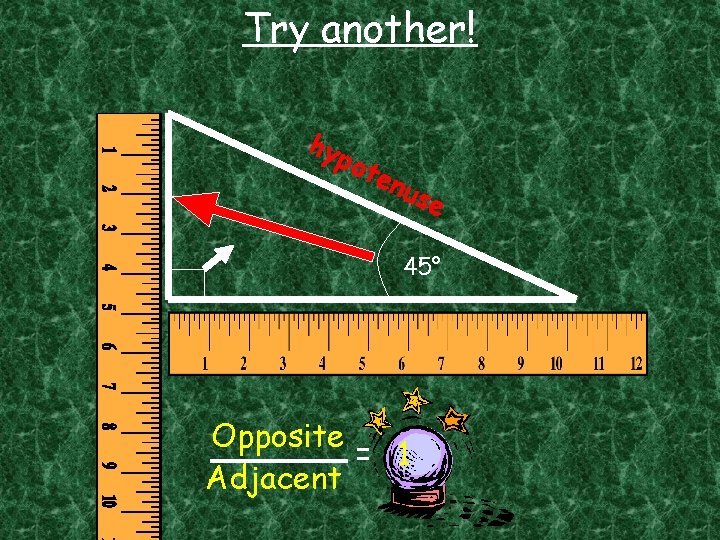
Try another! Opposite hy pot e nus e 45° Adjacent Opposite = 1 Adjacent

For an angle of 30°, Opposite = 0. 6 Adjacent Opposite is called the tangent of an angle. Adjacent We write tan 30° = 0. 6

The ancient Greeks discovered this and repeated this for all possible angles. Tan 25° 0. 466 Tan 26° 0. 488 Tan 27° 0. 510 Tan 28° 0. 532 Tan 29° 0. 554 Tan 30° = 0. 577 Tan 30° 0. 577 Tan 31° 0. 601 Tan 32° 0. 625 Tan 33° 0. 649 Tan 34° 0. 675 Accurate to 3 decimal places!

Now-a-days we can use calculators instead of tables to find the Tan of an angle. On your calculator press Followed by 30, and press Tan = Notice that your calculator is incredibly accurate!! Accurate to 9 decimal places!

What’s the point of all this? ? ? Don’t worry, you’re about to find out!

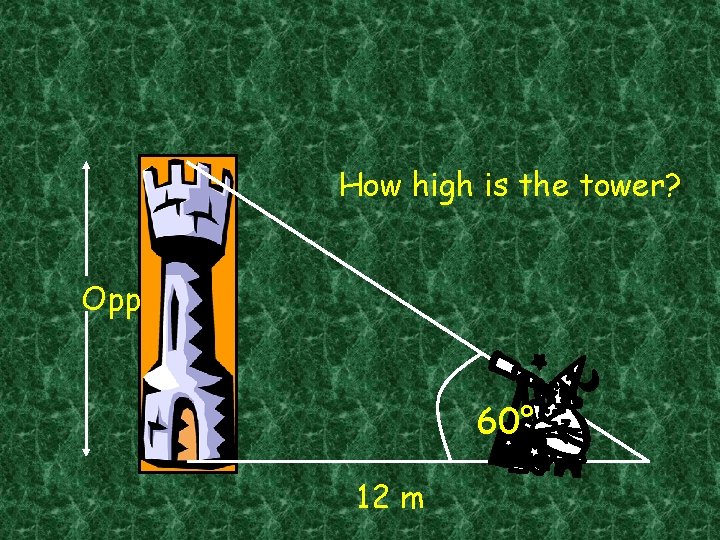
How high is the tower? Opp 60° 12 m

Opposite hy po t en us e 60° 12 m Adjacent Copy this!

Opp Tan x° = Adj Opp Tan 60° = 12 12 x Tan 60° = Opp =12 x Tan 60° = 20. 8 m (1 d. p. ) Copy this!

So the tower’s 20. 8 m high! 20. 8 m Don’t worry, you’ll be trying plenty of examples!!

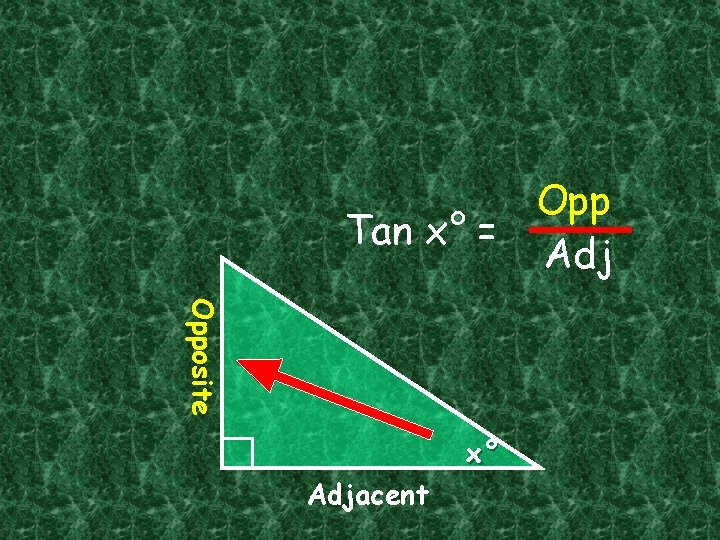
Opp Tan x° = Adj Opposite x° Adjacent

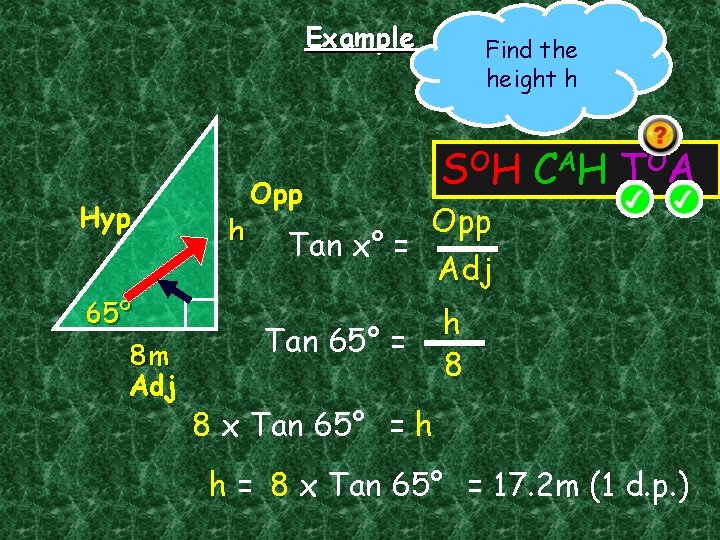
Example Hyp 65° 8 m Adj h Opp Tan x° = Find the height h S OH C A H T OA Opp Tan 65° = Adj h 8 8 x Tan 65° = h h = 8 x Tan 65° = 17. 2 m (1 d. p. )

Angles & Triangles Learning Intention 1. To use tan of the angle to solve problems. Success Criteria 1. Write down tan ratio. 2. Use tan of an angle to solve problems.

Using Tan to calculate angles

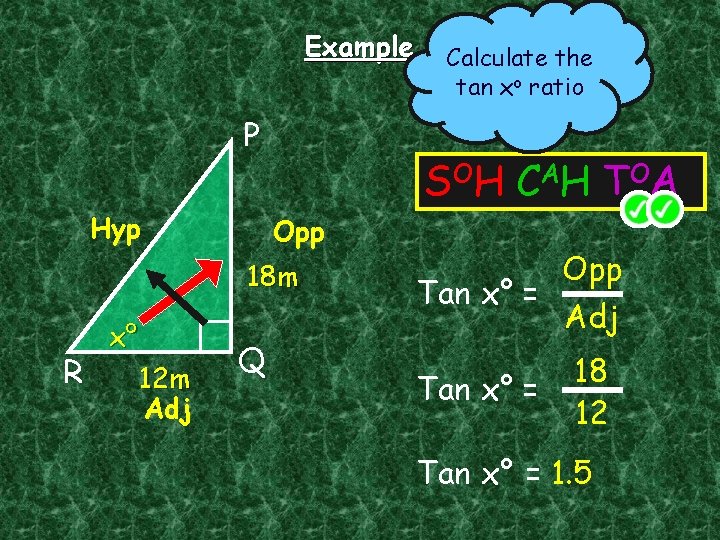
Example P Hyp S OH C A H T OA Opp 18 m R x° 12 m Adj Q Calculate the tan xo ratio Opp Tan x° = Adj Tan x° = 18 12 Tan x° = 1. 5

Calculate the size of angle xo Tan x° = 1. 5 How do we find x°? We need to use Tan ⁻¹on the calculator. Tan ⁻¹is written above To get this press 2 nd Tan ⁻¹ Tan Followed by Tan

Tan x° = 1. 5 Press 2 nd Enter 1. 5 Tan ⁻¹ Tan = x = Tan ⁻¹ 1. 5 = 56. 3° (1 d. p. )

Process 1. Identify Hyp, Opp and Adj 2. Write down ratio Tan xo = Opp Adj 3. Calculate xo 2 nd Tan ⁻¹ Tan

Angles & Triangles Learning Intention 1. To use tan of the angle to solve REAL LIFE problems. Success Criteria 1. Write down tan ratio. 2. Use tan of an angle to solve REAL LIFE problems.

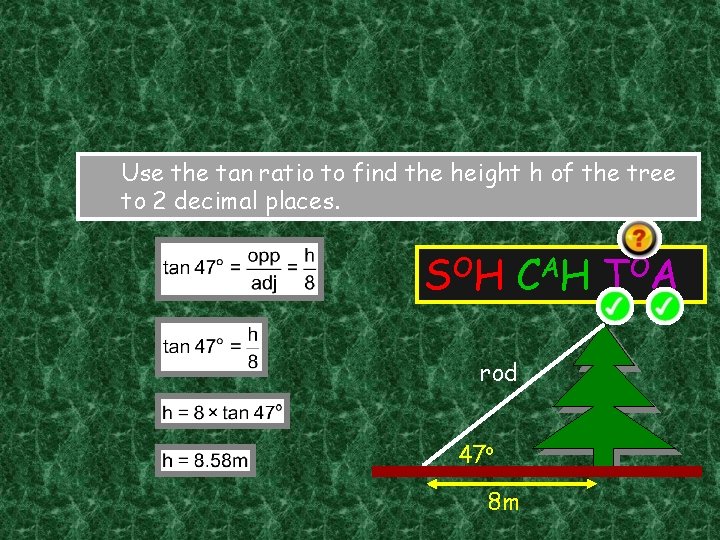
Use the tan ratio to find the height h of the tree to 2 decimal places. S OH C A H T OA rod 47 o 8 m

Example 2 S OH C A H T OA Q 1. An aeroplane is preparing to land at Glasgow Airport. It is over Lennoxtown at present which is 15 km from the airport. The angle of descent is 6 o. What is the height of the plane ? Aeroplane c 6 o Airport 19 -Feb-21 a = 15 Lennoxtown

Angles & Triangles Learning Intention 1. To use tan of the angle to find adjacent length. Success Criteria 1. Write down tan ratio. 2. Use tan of an angle to solve find adjacent length.

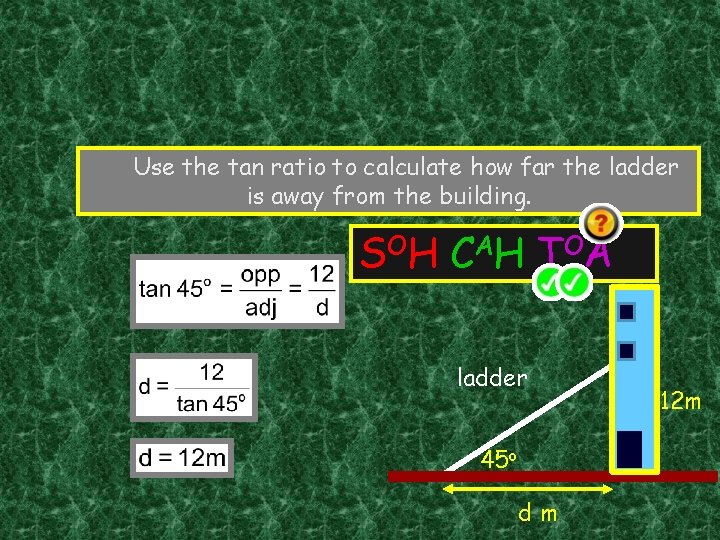
Use the tan ratio to calculate how far the ladder is away from the building. S OH C A H T OA ladder 45 o dm 12 m

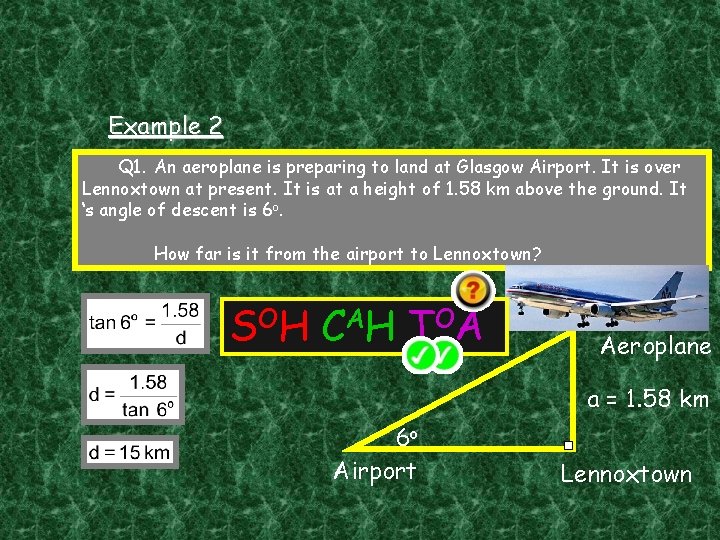
Example 2 Q 1. An aeroplane is preparing to land at Glasgow Airport. It is over Lennoxtown at present. It is at a height of 1. 58 km above the ground. It ‘s angle of descent is 6 o. How far is it from the airport to Lennoxtown? S OH C A H T OA Aeroplane a = 1. 58 km 6 o Airport Lennoxtown

Angles & Triangles Learning Intention 1. To show to find an angle using tan ratio. Success Criteria 1. Write down tan ratio. 2. Use tan ratio to find an angle.

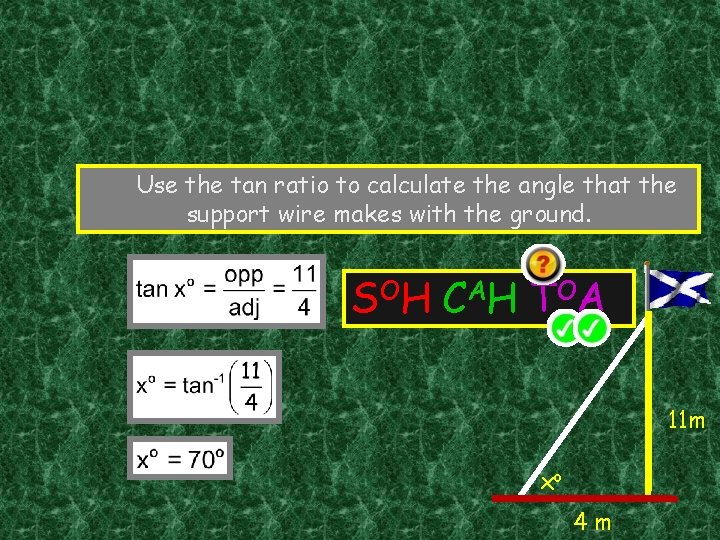
Use the tan ratio to calculate the angle that the support wire makes with the ground. S OH C A H T OA 11 m xo 4 m

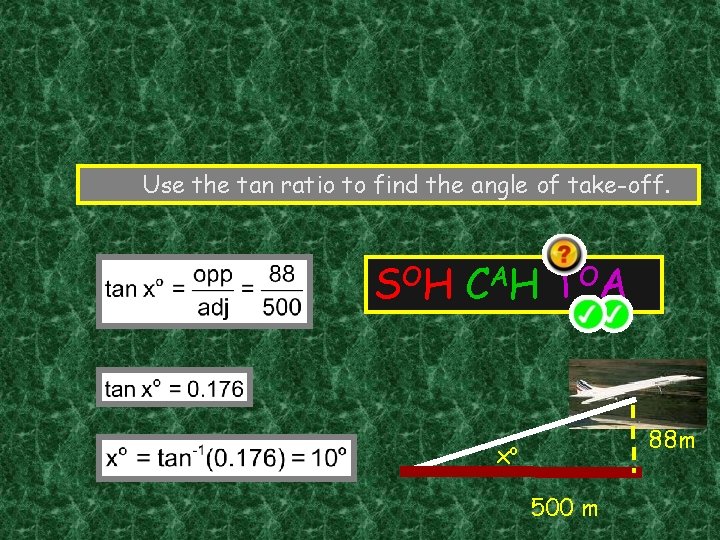
Use the tan ratio to find the angle of take-off. S OH C A H T OA 88 m xo 500 m

Angles & Triangles Learning Intention 1. Definite the sine ratio and show to find an angle using this ratio. Success Criteria 1. Write down sine ratio. 2. Use sine ratio to find an angle.

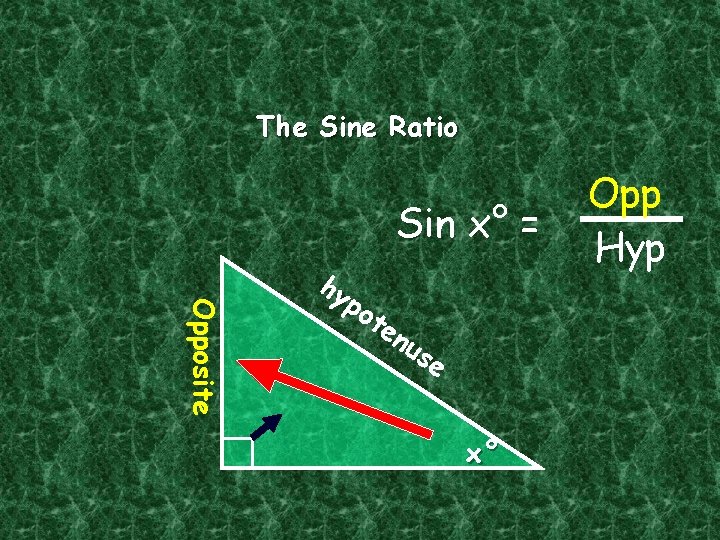
The Sine Ratio Sin x° = Opposite hy po t en us e x° Opp Hyp

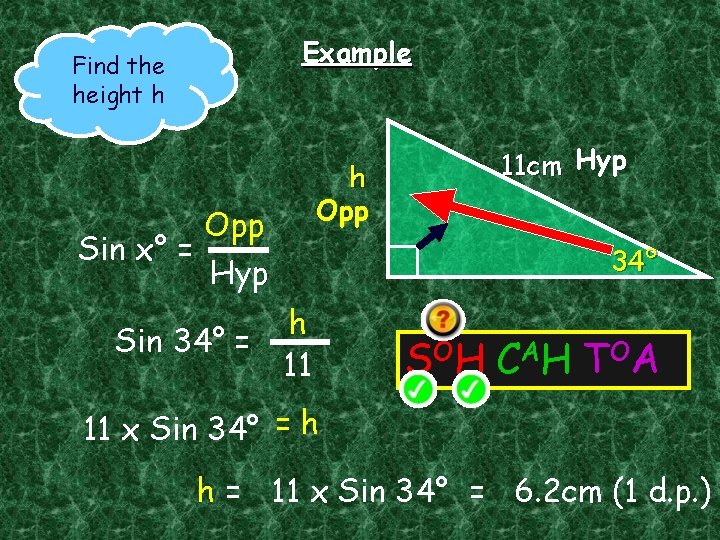
Example Find the height h Sin x° = h Opp 34° Hyp Sin 34° = 11 cm Hyp h 11 S OH C A H T OA 11 x Sin 34° = h h = 11 x Sin 34° = 6. 2 cm (1 d. p. )

Using Sin to calculate angles

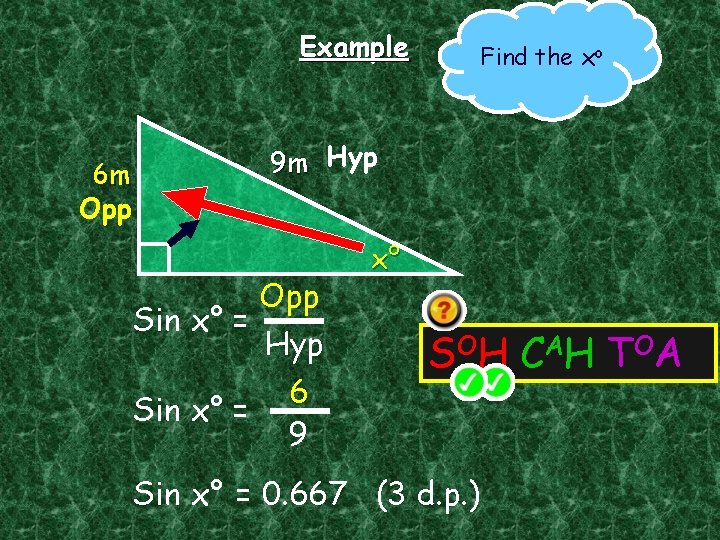
Example 6 m Opp Find the xo 9 m Hyp Opp Sin x° = Hyp 6 Sin x° = 9 x° S OH C A H T OA Sin x° = 0. 667 (3 d. p. )

Sin x° =0. 667 (3 d. p. ) How do we find x°? We need to use Sin ⁻¹on the calculator. Sin ⁻¹is written above To get this press 2 nd Sin ⁻¹ Sin Followed by Sin

Sin x° = 0. 667 (3 d. p. ) Press 2 nd Enter 0. 667 Sin ⁻¹ Sin = x = Sin ⁻¹ 0. 667 = 41. 8° (1 d. p. )

Angles & Triangles Learning Intention 1. To show to use the sine ratio to solve Success Criteria 1. Write down sine ratio. REAL-LIFE problems. 2. Use sine ratio to solve REAL-LIFE problems.

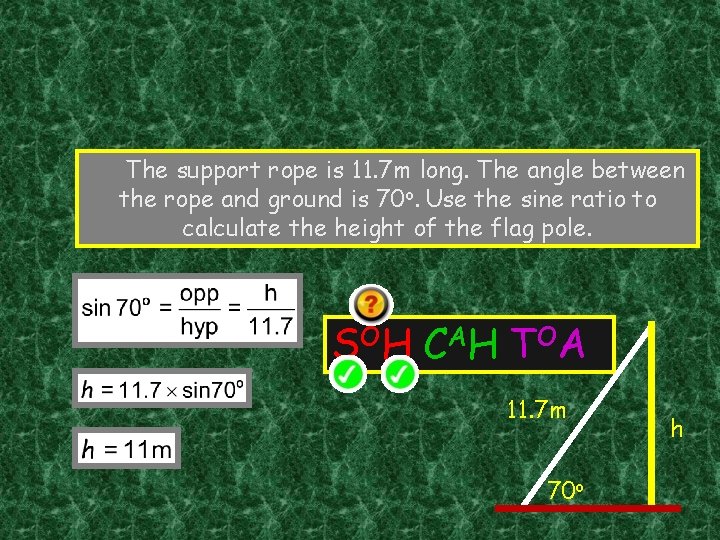
The support rope is 11. 7 m long. The angle between the rope and ground is 70 o. Use the sine ratio to calculate the height of the flag pole. S OH C A H T OA 11. 7 m 70 o h

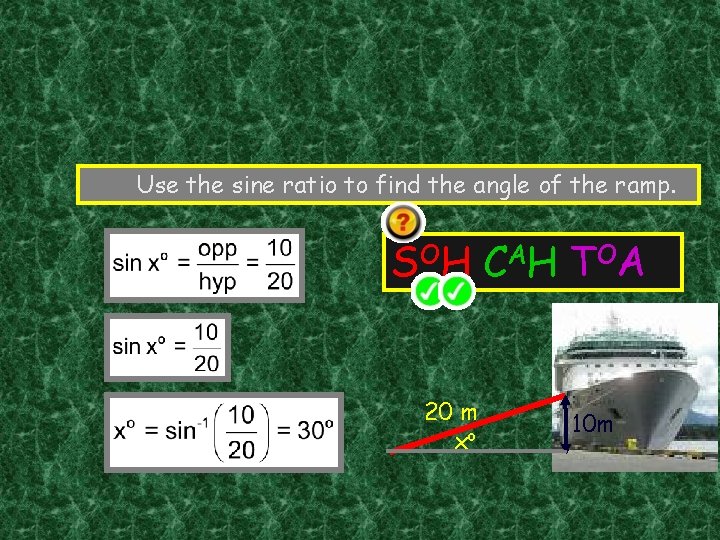
Use the sine ratio to find the angle of the ramp. S OH C A H T OA 20 m xo 10 m

Angles & Triangles Learning Intention 1. To show to calculate the hypotenuse using the sine ratio. Success Criteria 1. Write down sine ratio. 2. Use sine ratio to find the hypotenuse.

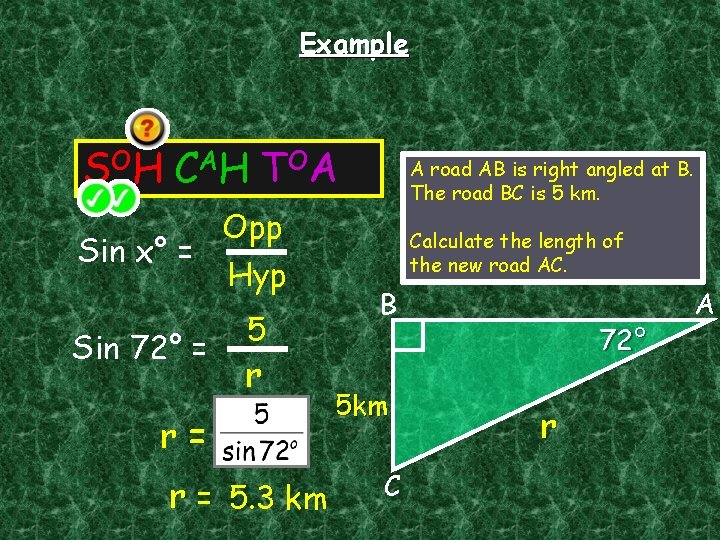
Example S OH C A H T OA Sin x° = Sin 72° = A road AB is right angled at B. The road BC is 5 km. Opp Hyp 5 r r= r = 5. 3 km Calculate the length of the new road AC. B 5 km C 72° r A

Angles & Triangles Learning Intention 1. Definite the cosine ratio and show to find an length or angle using this ratio. Success Criteria 1. Write down cosine ratio. 2. Use cosine ratio to find a length or angle.

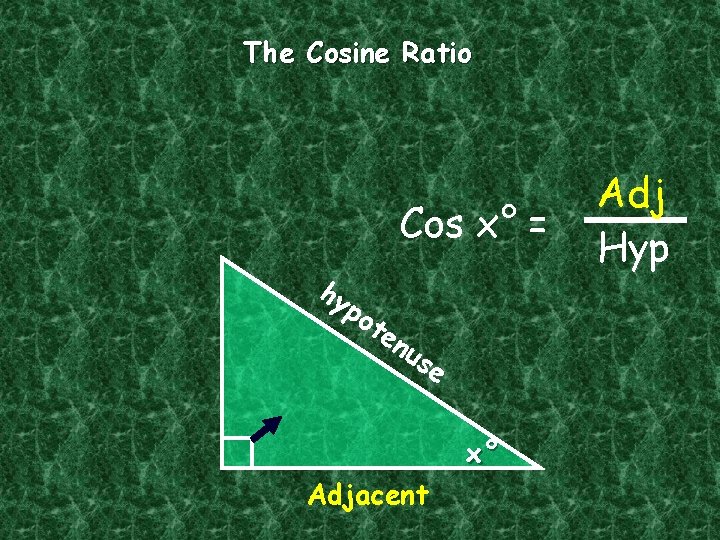
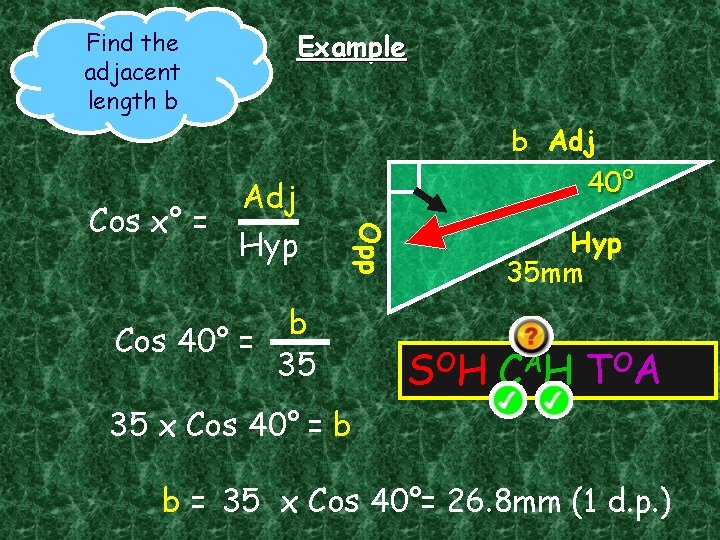
The Cosine Ratio Cos x° = hy po t en us e x° Adjacent Adj Hyp

Find the adjacent length b Example Opp Adj Cos x° = Hyp b Adj 40° b Cos 40° = 35 Hyp 35 mm S OH C A H T OA 35 x Cos 40° = b b = 35 x Cos 40°= 26. 8 mm (1 d. p. )

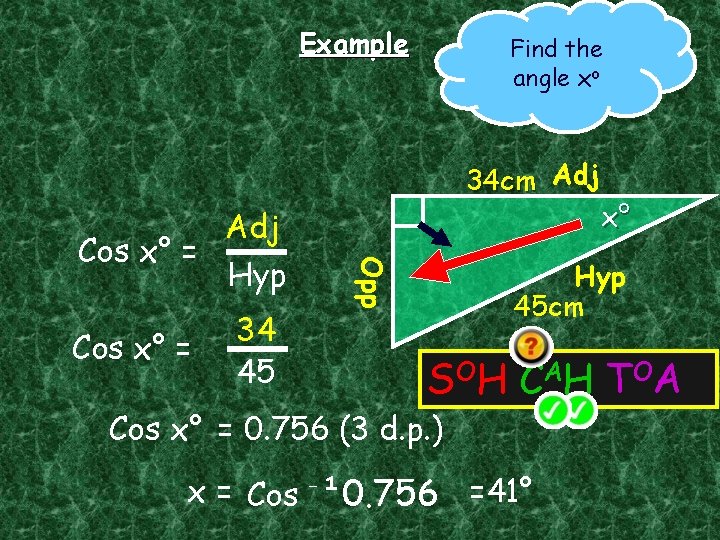
Using Cos to calculate angles

Example Find the angle xo 34 cm Adj Cos x° = x° Hyp 45 cm 34 45 Opp Cos x° = Adj S OH C A H T OA Cos x° = 0. 756 (3 d. p. ) x = Cos ⁻¹ 0. 756 =41°

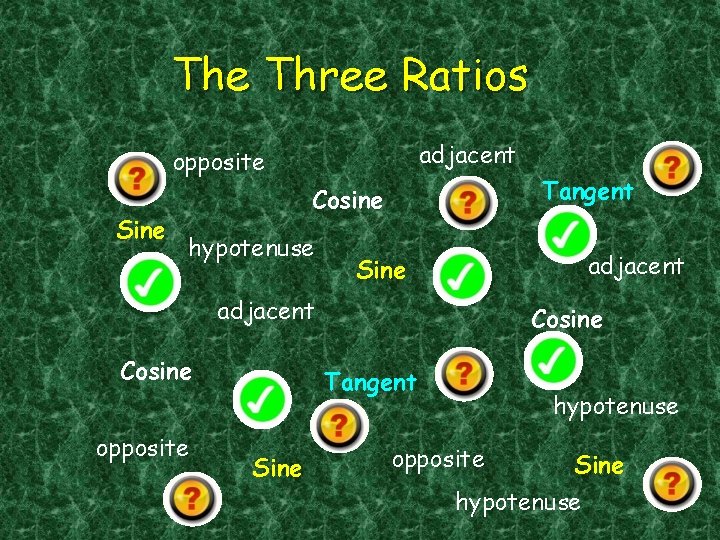
The Three Ratios adjacent opposite Sine Tangent Cosine hypotenuse adjacent Sine adjacent Cosine opposite Cosine Tangent Sine hypotenuse opposite Sine hypotenuse

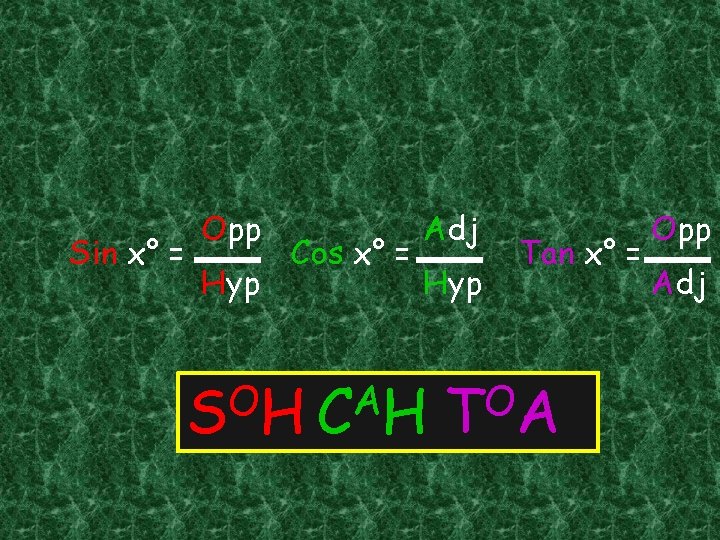
Sin x° = Opp Hyp Cos x° = Adj Hyp O A S HC H Tan x° = O T A Opp Adj

Process 1. Write down S OH C A H T OA 2. 3. Identify what you want to find what you know Copy this!

Past Paper Type Questions S OH C A H T OA

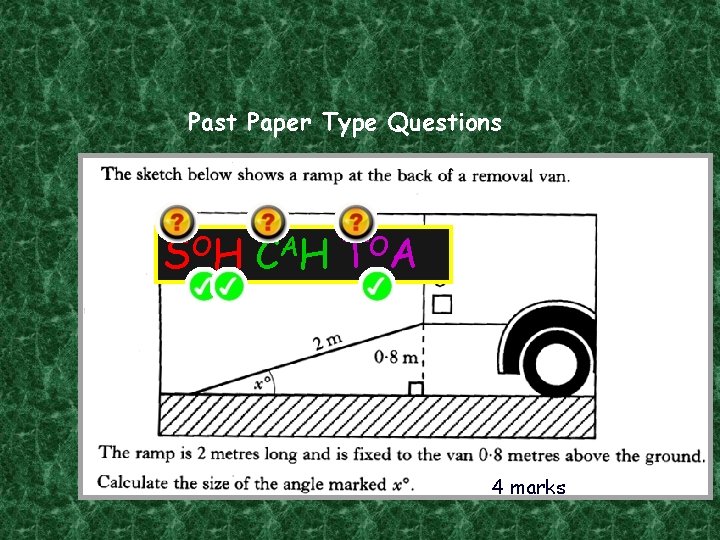
Past Paper Type Questions S OH C A H T OA (4 marks)

Past Paper Type Questions S OH C A H T OA

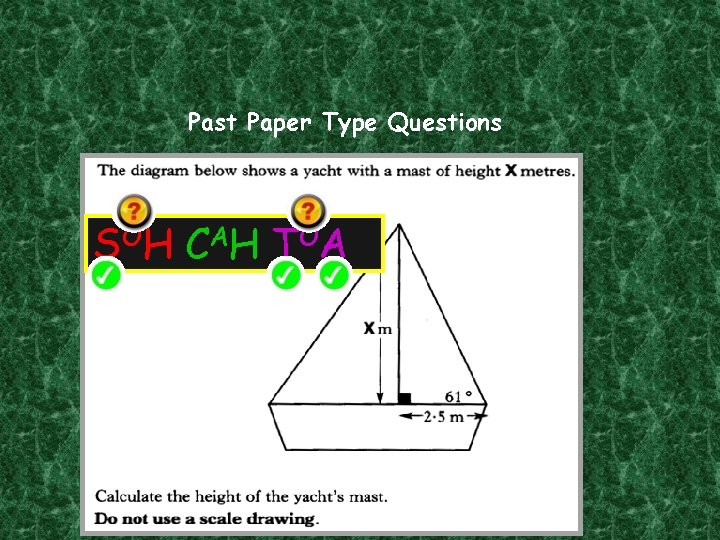
Past Paper Type Questions S OH C A H T OA 4 marks

Past Paper Type Questions S OH C A H T OA

Past Paper Type Questions S OH C A H T OA (4 marks)

Past Paper Type Questions S OH C A H T OA

Past Paper Type Questions S OH C A H T OA (4 marks)
 Secant tangent angles
Secant tangent angles Tan ratio
Tan ratio Internal tangent vs external tangent
Internal tangent vs external tangent 40²+30²
40²+30² Trigonometric ratios worksheet
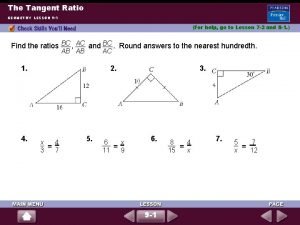
Trigonometric ratios worksheet Practice 9-1 the tangent ratio
Practice 9-1 the tangent ratio Tangent ratio
Tangent ratio Tan ratio
Tan ratio Word splash examples
Word splash examples Sine ratio
Sine ratio Tangent ratio
Tangent ratio Diameter theorem
Diameter theorem Secant and tangent angles
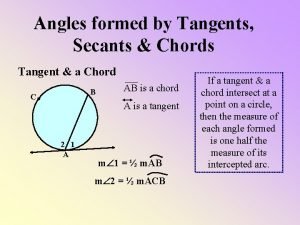
Secant and tangent angles Angles formed by chords, tangents, secants
Angles formed by chords, tangents, secants Tangent formula
Tangent formula Hazard ratio vs odds ratio
Hazard ratio vs odds ratio It is the reciprocal of velocity ratio
It is the reciprocal of velocity ratio Acid test ratio and quick ratio
Acid test ratio and quick ratio Fixed interval vs fixed ratio
Fixed interval vs fixed ratio Dihybrid cross genotypic ratio
Dihybrid cross genotypic ratio Perbedaan or rr dan pr
Perbedaan or rr dan pr Current ratio and quick ratio
Current ratio and quick ratio Angle-angle similarity postulate
Angle-angle similarity postulate Critical angle formula
Critical angle formula Third angle orthographic projection symbol
Third angle orthographic projection symbol What is an angle whose vertex is the center of the circle
What is an angle whose vertex is the center of the circle Rotary instruments in dentistry
Rotary instruments in dentistry Absolute angle vs relative angle
Absolute angle vs relative angle Adjacent angles linear pair
Adjacent angles linear pair Name an angle adjacent to angle fgi
Name an angle adjacent to angle fgi Angle klm and angle mln are a linear pair.
Angle klm and angle mln are a linear pair. Angle bisector worksheet
Angle bisector worksheet Angle bisector steps
Angle bisector steps Types of extinction in minerals
Types of extinction in minerals Angle 1 and angle 2 are complementary
Angle 1 and angle 2 are complementary Lip angle of drill
Lip angle of drill Angle of depression
Angle of depression Vertically opposite angles
Vertically opposite angles Postulates
Postulates Lesson 4 measuring angles
Lesson 4 measuring angles First angle
First angle Risk reward ratio
Risk reward ratio A ratio is a comparison of two numbers
A ratio is a comparison of two numbers Tape diagram definition
Tape diagram definition Sin of an obtuse angle
Sin of an obtuse angle Rewrite using a double-angle identity. a. b. c. d.
Rewrite using a double-angle identity. a. b. c. d. Using system.collections
Using system.collections Defrost using internal heat is accomplished using
Defrost using internal heat is accomplished using Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Chụp tư thế worms-breton
Chụp tư thế worms-breton Chúa yêu trần thế
Chúa yêu trần thế Môn thể thao bắt đầu bằng chữ đua
Môn thể thao bắt đầu bằng chữ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng