Tangent Lines Understanding Tangent Lines A tangent to

  • Slides: 22
Download presentation
Tangent Lines

Tangent Lines

Understanding Tangent Lines • A tangent to a circle is a line that intersects

Understanding Tangent Lines • A tangent to a circle is a line that intersects a circle in exactly one point. • The point where a circle and a tangent intersect is the point of tangency. Theorem 12 -1: If a line is tangent to a circle, then the line is perpendicular to the radius at the point of tangency.

Finding Angle Measures • ML and MN are tangent to O. What is the

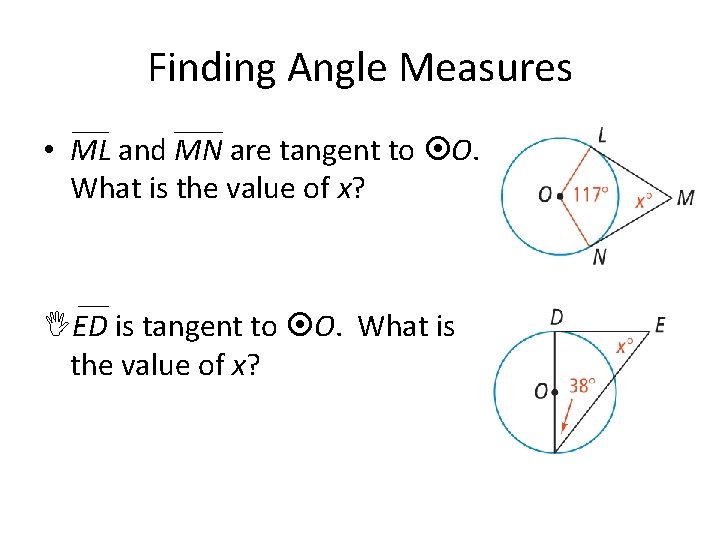
Finding Angle Measures • ML and MN are tangent to O. What is the value of x? ED is tangent to O. What is the value of x?

Finding a Radius • What is the radius of C? What is the radius

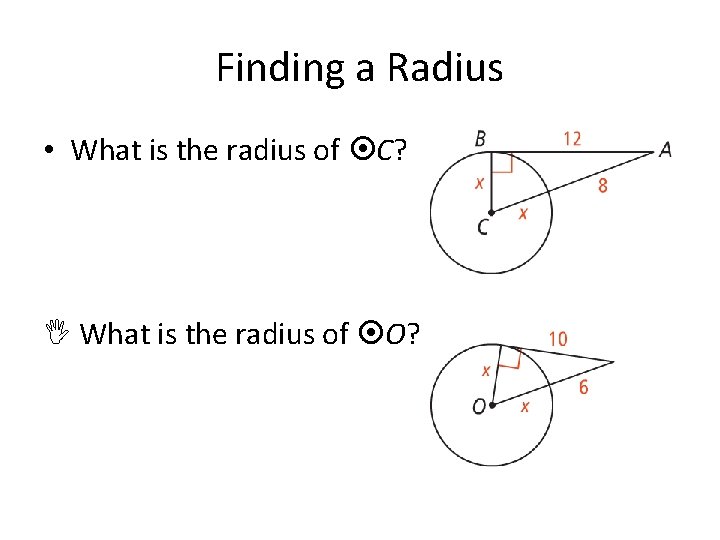
Finding a Radius • What is the radius of C? What is the radius of O?

More Tangent Theorems Theorem 12 -2: If two tangent segments to a circle share

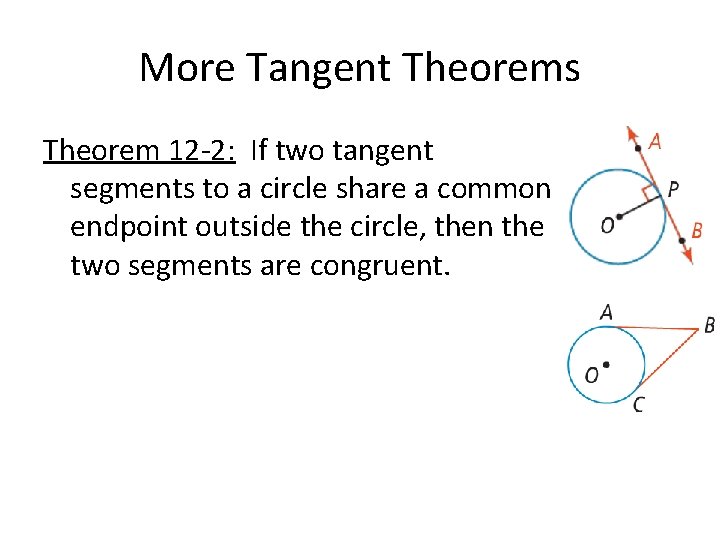
More Tangent Theorems Theorem 12 -2: If two tangent segments to a circle share a common endpoint outside the circle, then the two segments are congruent.

Identifying a Tangent • Is ML tangent to N at L? Use the diagram

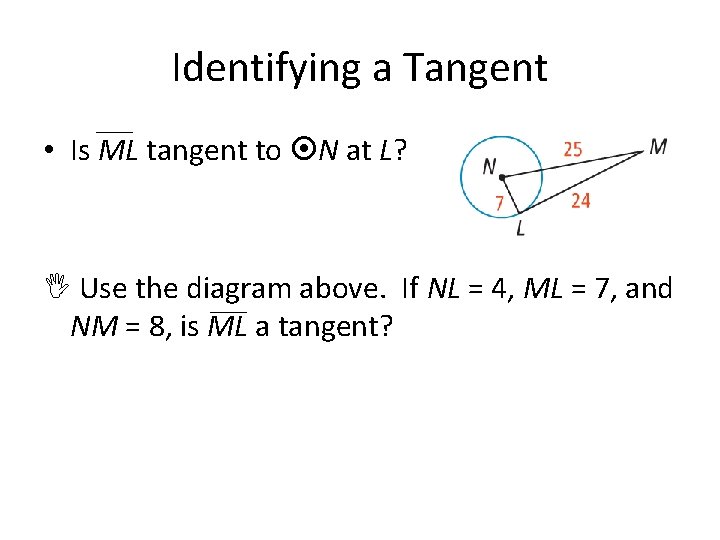
Identifying a Tangent • Is ML tangent to N at L? Use the diagram above. If NL = 4, ML = 7, and NM = 8, is ML a tangent?

Circles Inscribed in Polygons • What is the perimeter of ΔABC? If the perimeter

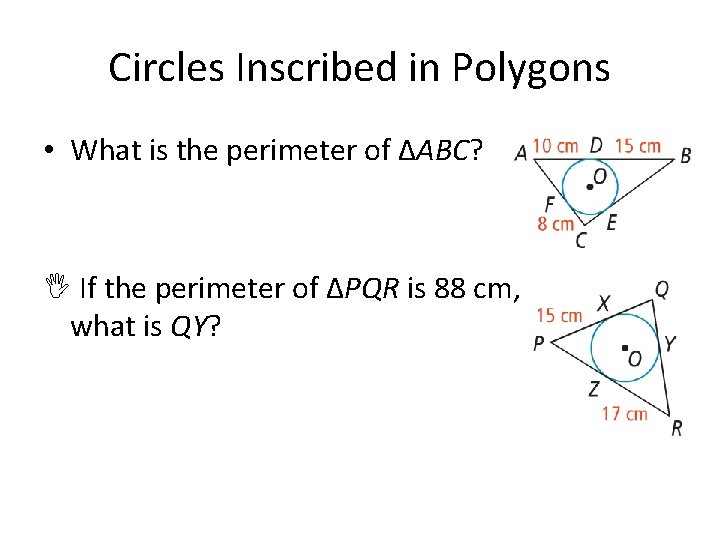
Circles Inscribed in Polygons • What is the perimeter of ΔABC? If the perimeter of ΔPQR is 88 cm, what is QY?

Chords and Arcs

Chords and Arcs

Chords • A chord is a segment whose endpoints are on a circle. Theorem

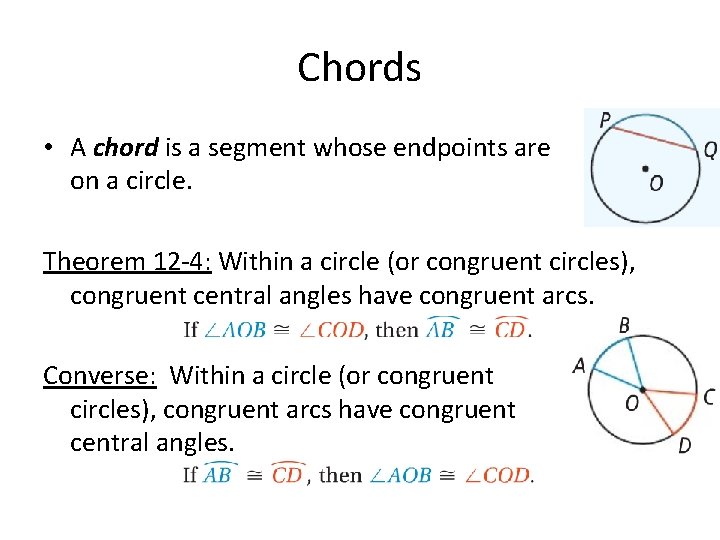
Chords • A chord is a segment whose endpoints are on a circle. Theorem 12 -4: Within a circle (or congruent circles), congruent central angles have congruent arcs. Converse: Within a circle (or congruent circles), congruent arcs have congruent central angles.

More About Chords Theorem 12 -5: Within a circle (or congruent circles), congruent central

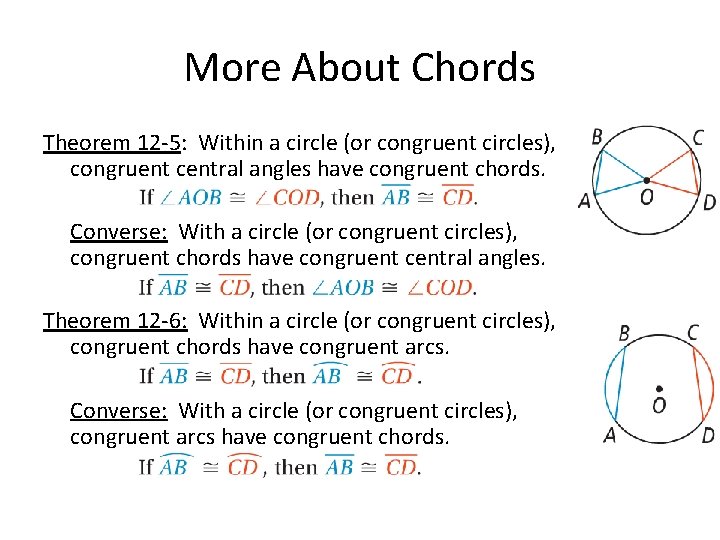
More About Chords Theorem 12 -5: Within a circle (or congruent circles), congruent central angles have congruent chords. Converse: With a circle (or congruent circles), congruent chords have congruent central angles. Theorem 12 -6: Within a circle (or congruent circles), congruent chords have congruent arcs. Converse: With a circle (or congruent circles), congruent arcs have congruent chords.

Using Congruent Chords In the diagram, O P. Given that BC DF, what can

Using Congruent Chords In the diagram, O P. Given that BC DF, what can you conclude?

Still More About Chords Theorem 12 -7: Within a circle (or congruent circles), chords

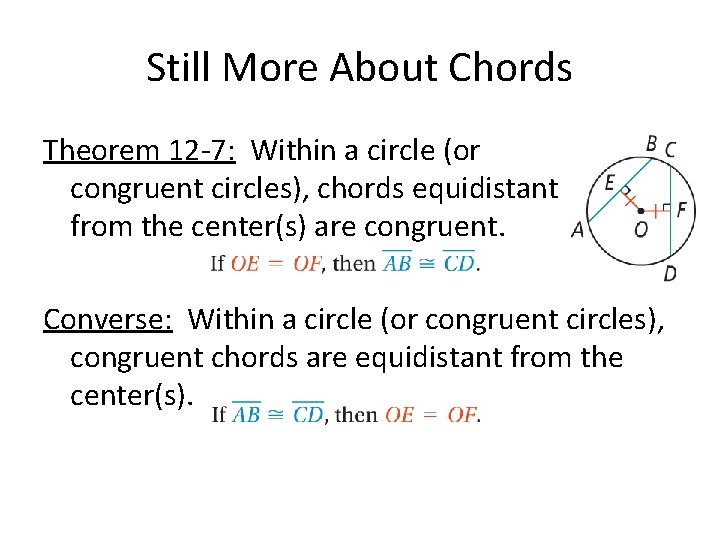
Still More About Chords Theorem 12 -7: Within a circle (or congruent circles), chords equidistant from the center(s) are congruent. Converse: Within a circle (or congruent circles), congruent chords are equidistant from the center(s).

Even More About Chords Theorem 12 -8: In a circle, if a diameter is

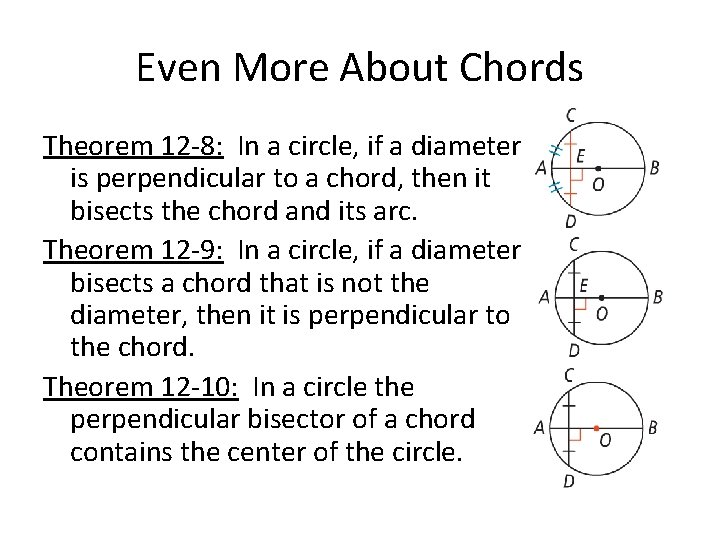
Even More About Chords Theorem 12 -8: In a circle, if a diameter is perpendicular to a chord, then it bisects the chord and its arc. Theorem 12 -9: In a circle, if a diameter bisects a chord that is not the diameter, then it is perpendicular to the chord. Theorem 12 -10: In a circle the perpendicular bisector of a chord contains the center of the circle.

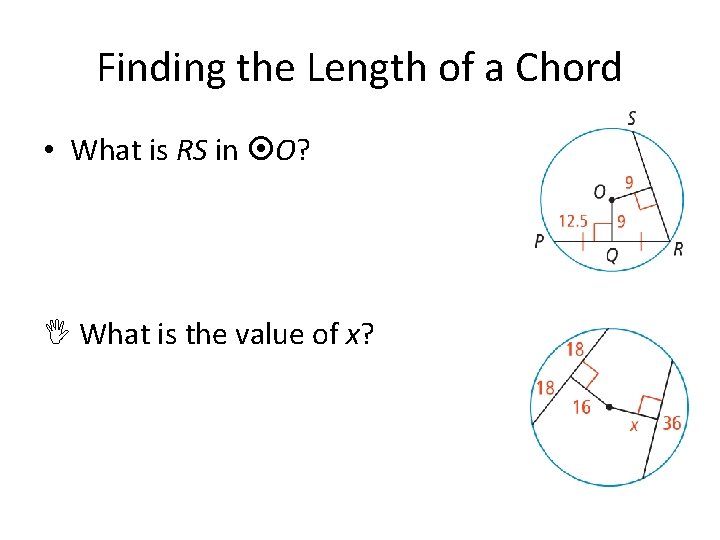
Finding the Length of a Chord • What is RS in O? What is

Finding the Length of a Chord • What is RS in O? What is the value of x?

Finding Measures in a Circle • What is the value of r to the

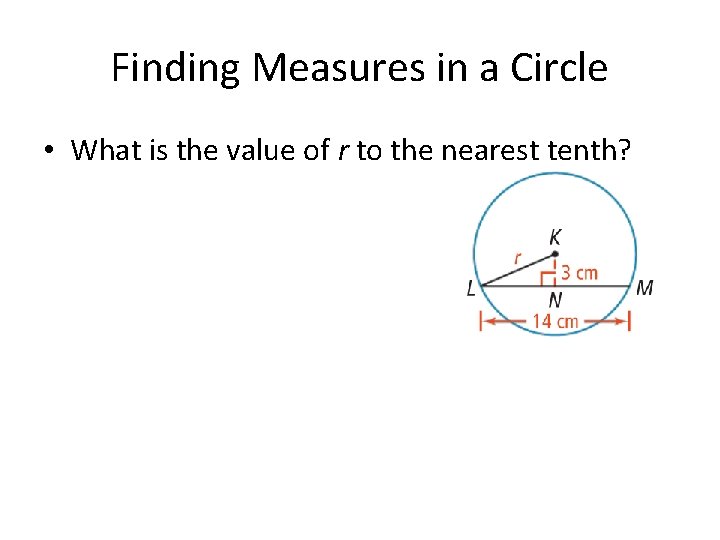
Finding Measures in a Circle • What is the value of r to the nearest tenth?

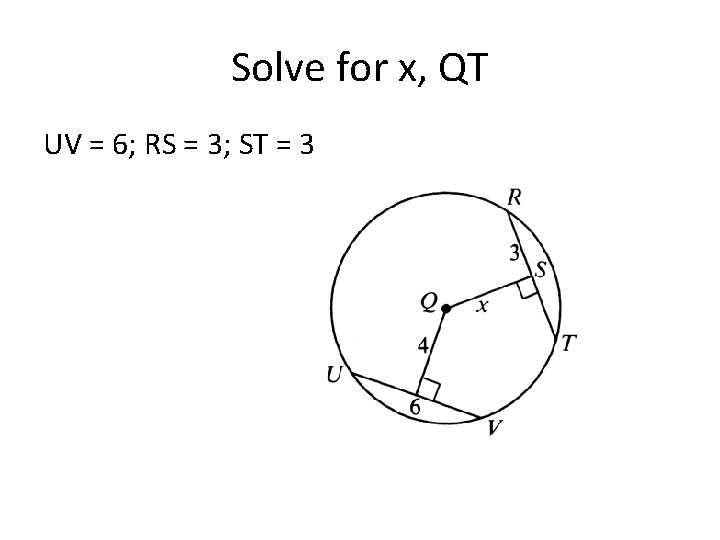
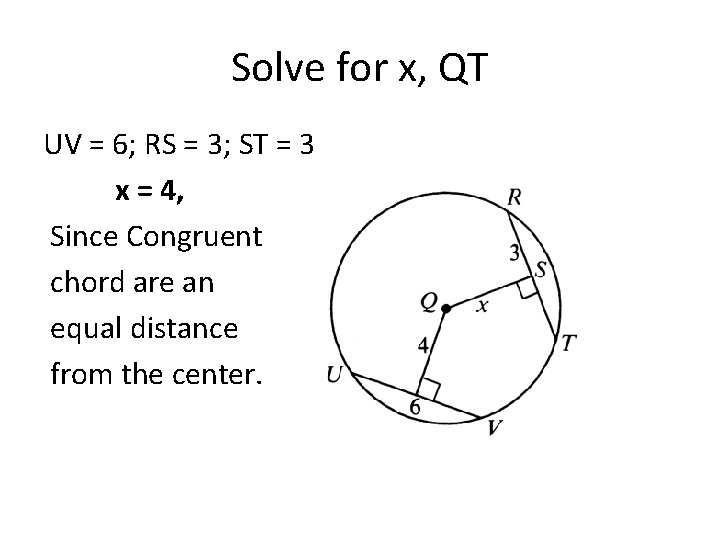
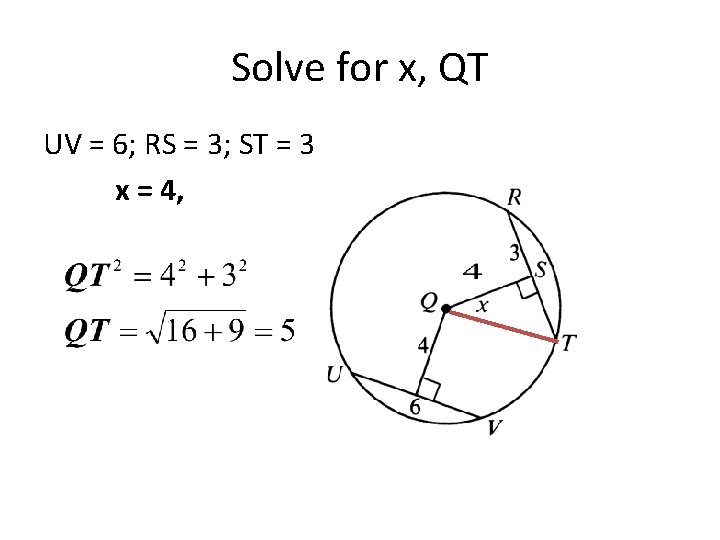
Solve for x, QT UV = 6; RS = 3; ST = 3

Solve for x, QT UV = 6; RS = 3; ST = 3

Solve for x, QT UV = 6; RS = 3; ST = 3 x

Solve for x, QT UV = 6; RS = 3; ST = 3 x = 4, Since Congruent chord are an equal distance from the center.

Solve for x, QT UV = 6; RS = 3; ST = 3 x

Solve for x, QT UV = 6; RS = 3; ST = 3 x = 4,

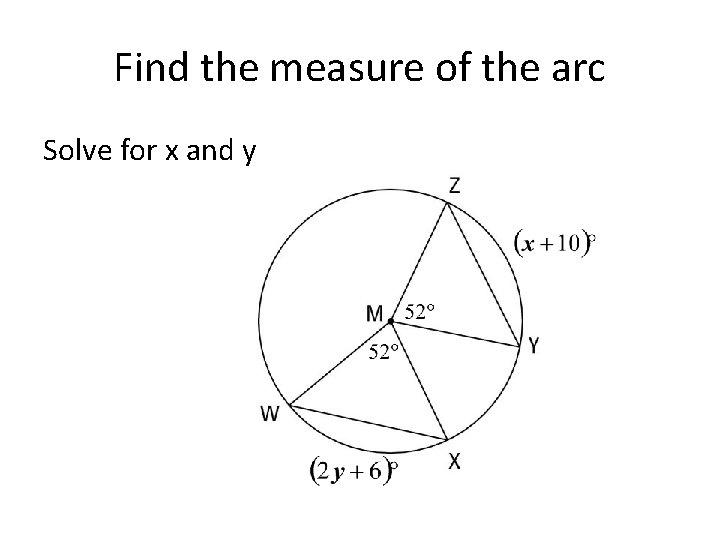
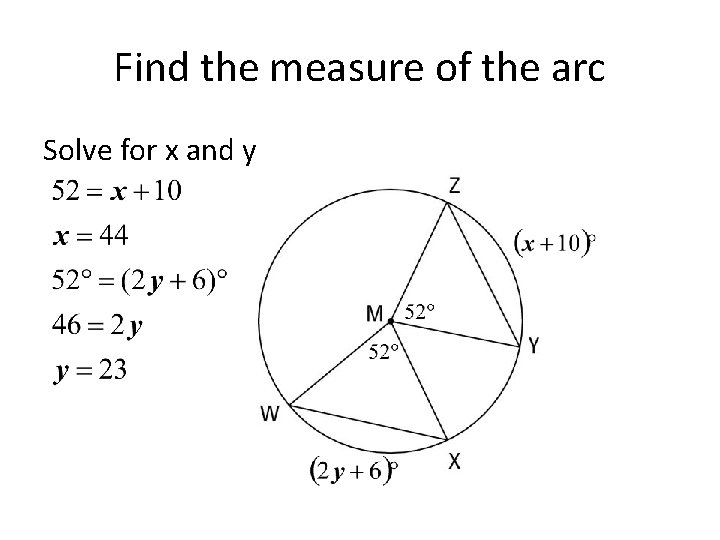
Find the measure of the arc Solve for x and y

Find the measure of the arc Solve for x and y

Find the measure of the arc Solve for x and y

Find the measure of the arc Solve for x and y

D 2 x° (x + 40)°

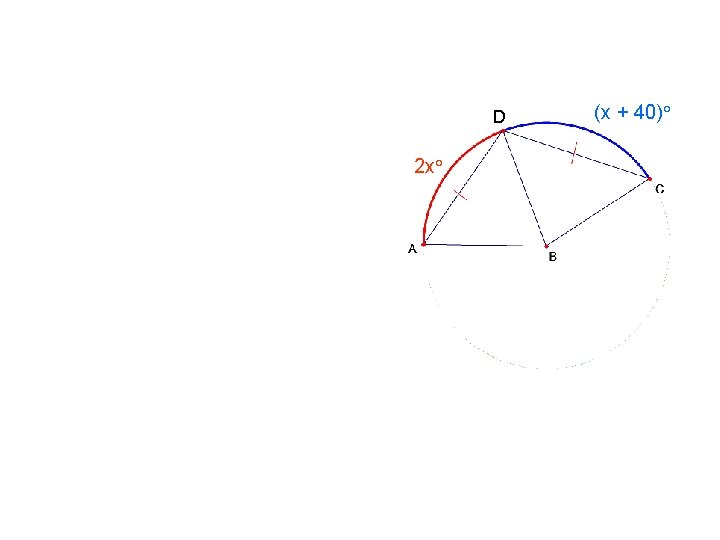
D 2 x° (x + 40)°

Ex. 3: Using Theorem 10. 4 AB = 8; DE = 8, and CD

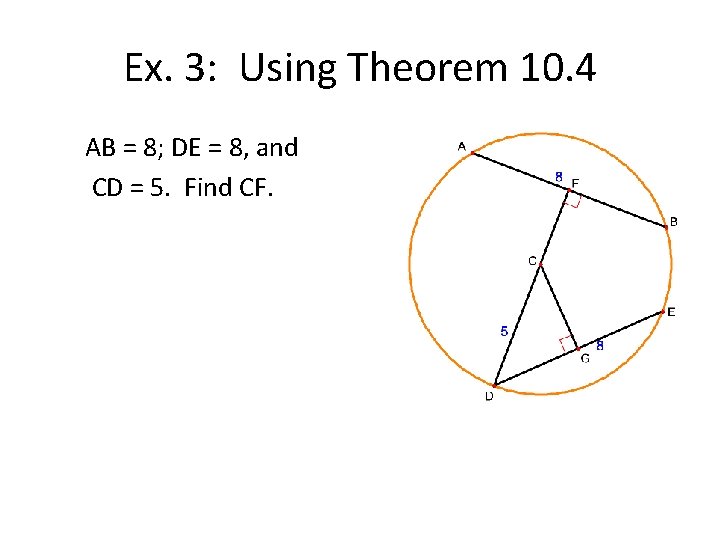
Ex. 3: Using Theorem 10. 4 AB = 8; DE = 8, and CD = 5. Find CF.

2 72 8 TANGENT LINES DERIVATIVES TANGENT LINE2 72 8 TANGENT LINES DERIVATIVES TANGENT LINE
Tangent lines n Recall tangent line is theTangent lines n Recall tangent line is the
11 1 Tangent Lines Chapter 11 Circles Tangent11 1 Tangent Lines Chapter 11 Circles Tangent
Tangent Lines 1 Equation of lines 2 EquationTangent Lines 1 Equation of lines 2 Equation
How Secant Lines become Tangent Lines Adrienne SamanthaHow Secant Lines become Tangent Lines Adrienne Samantha
10 1 Tangent Ratios Obj Use tangent to10 1 Tangent Ratios Obj Use tangent to
Tangent and Cotangent Graphs Reading and Drawing TangentTangent and Cotangent Graphs Reading and Drawing Tangent
The Tangent Ratio The Tangent using Angle TheThe Tangent Ratio The Tangent using Angle The
Tangent Line Approximations A tangent line approximation isTangent Line Approximations A tangent line approximation is
The Tangent and Velocity Problems The Tangent ProblemThe Tangent and Velocity Problems The Tangent Problem
13 4 Tangent Ratio 13 4 Tangent Ratio13 4 Tangent Ratio 13 4 Tangent Ratio
The Slope of the Tangent Line The TangentThe Slope of the Tangent Line The Tangent
Tangent Line Recall from geometry Tangent is aTangent Line Recall from geometry Tangent is a
14 4 Tangent Planes Differential Elements Tangent Planes14 4 Tangent Planes Differential Elements Tangent Planes
Part 1 Coinciding Lines Parallel Lines Coinciding LinesPart 1 Coinciding Lines Parallel Lines Coinciding Lines
Skew Lines Skew Lines The two given linesSkew Lines Skew Lines The two given lines
Relationships Between Lines Parallel Lines two lines thatRelationships Between Lines Parallel Lines two lines that
GEOMETRY Angles and Parallel Lines Intersecting Lines LinesGEOMETRY Angles and Parallel Lines Intersecting Lines Lines
Pairs of Lines 1 Parallel Lines Parallel linesPairs of Lines 1 Parallel Lines Parallel lines
Angles and Parallel Lines Intersecting Lines Lines thatAngles and Parallel Lines Intersecting Lines Lines that
County Lines Solihull County Lines Definition County linesCounty Lines Solihull County Lines Definition County lines