9 5 Tangents to Circles Geometry Objectives Identify

9. 5 Tangents to Circles Geometry

Objectives �Identify segments and lines related to circles. �Use properties of a tangent to a circle.

Some definitions you need �Circle – set of all points in a plane that are equidistant from a given point called a center of the circle. A circle with center P is called “circle P”, or P. �The distance from the center to a point on the circle is called the radius of the circle. Two circles are congruent if they have the same radius.
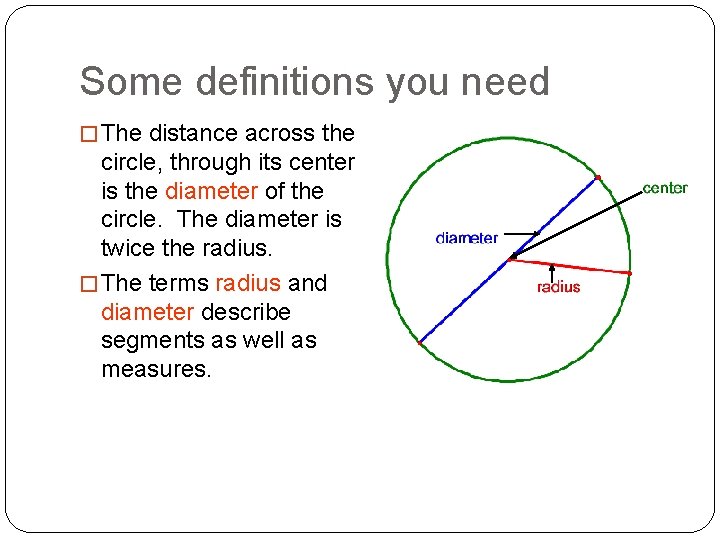
Some definitions you need � The distance across the circle, through its center is the diameter of the circle. The diameter is twice the radius. � The terms radius and diameter describe segments as well as measures.
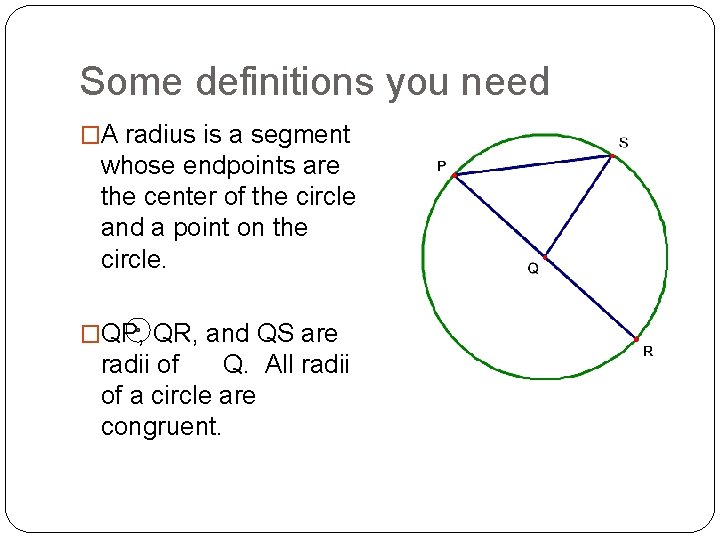
Some definitions you need �A radius is a segment whose endpoints are the center of the circle and a point on the circle. �QP, QR, and QS are radii of Q. All radii of a circle are congruent.
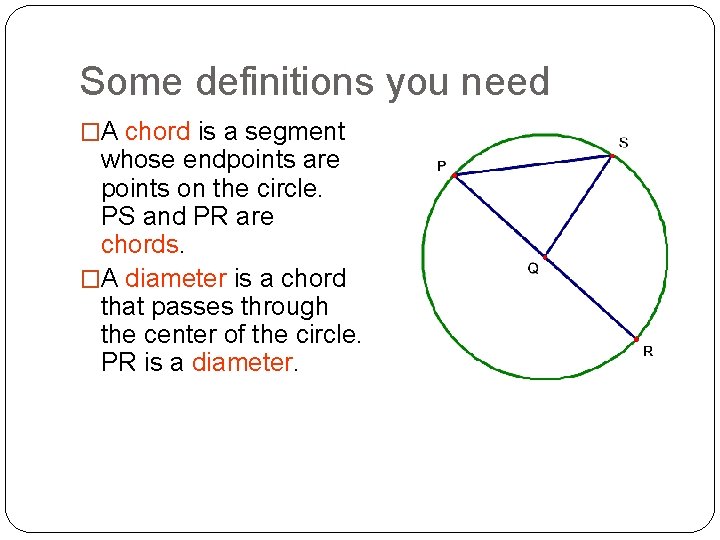
Some definitions you need �A chord is a segment whose endpoints are points on the circle. PS and PR are chords. �A diameter is a chord that passes through the center of the circle. PR is a diameter.
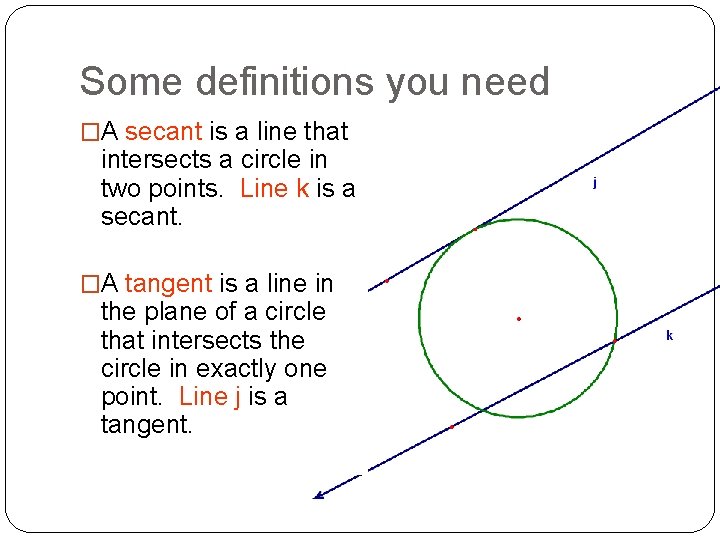
Some definitions you need �A secant is a line that intersects a circle in two points. Line k is a secant. �A tangent is a line in the plane of a circle that intersects the circle in exactly one point. Line j is a tangent.
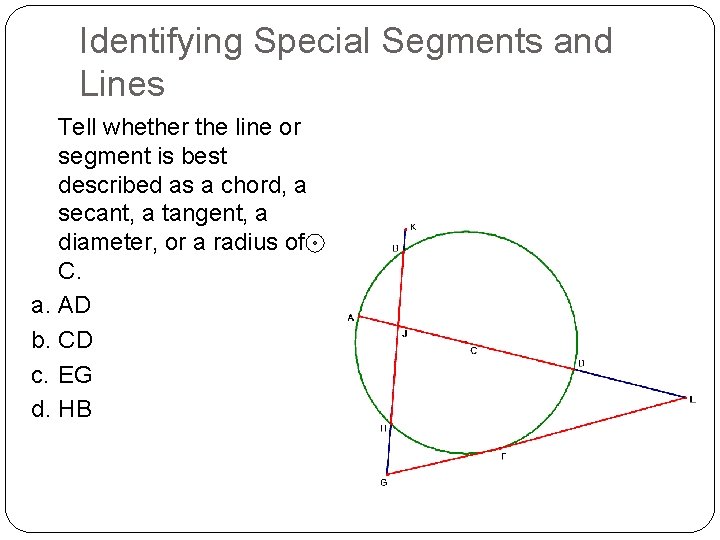
Identifying Special Segments and Lines Tell whether the line or segment is best described as a chord, a secant, a tangent, a diameter, or a radius of C. a. AD b. CD c. EG d. HB

More information you need-� In a plane, two circles can intersect in two points, one point, or no points. Coplanar circles that intersect in one point are called tangent circles. Coplanar circles that have a common center are called concentric. 2 points of intersection.
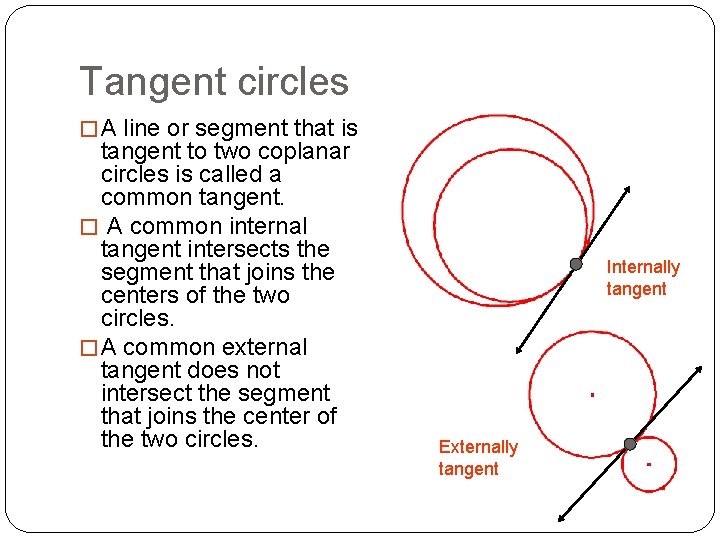
Tangent circles � A line or segment that is tangent to two coplanar circles is called a common tangent. � A common internal tangent intersects the segment that joins the centers of the two circles. � A common external tangent does not intersect the segment that joins the center of the two circles. Internally tangent Externally tangent
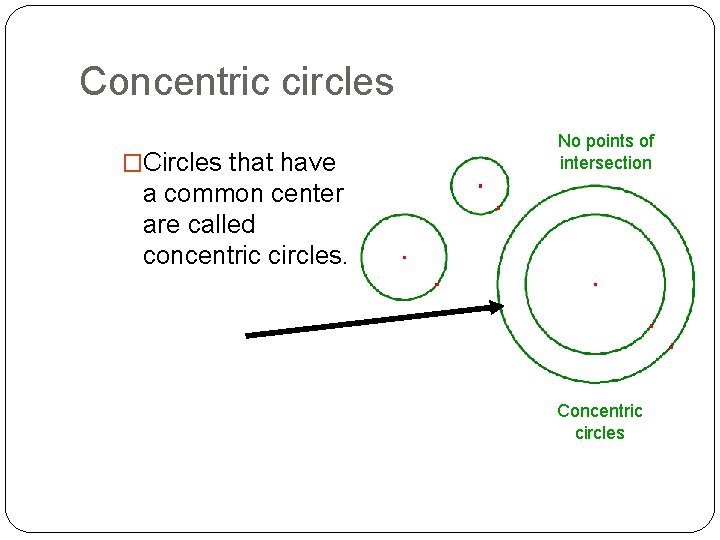
Concentric circles �Circles that have No points of intersection a common center are called concentric circles. Concentric circles
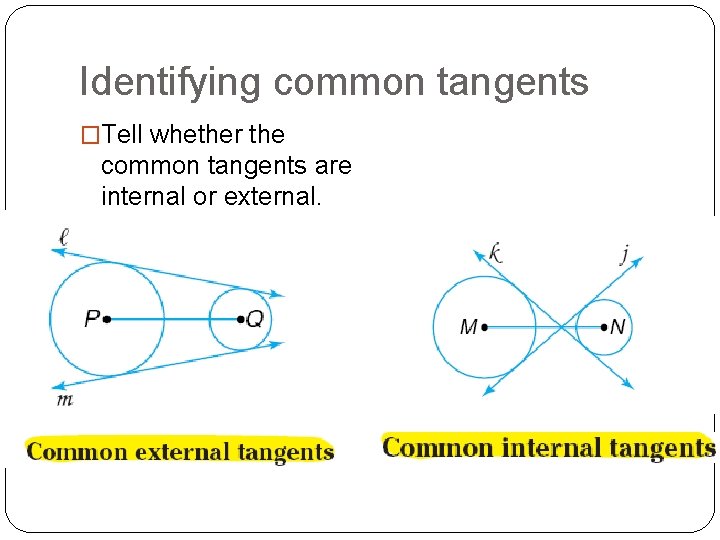
Identifying common tangents �Tell whether the common tangents are internal or external.
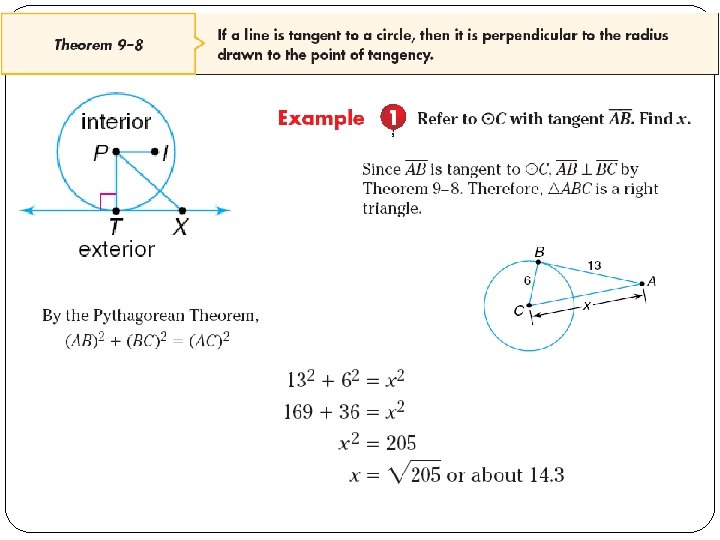

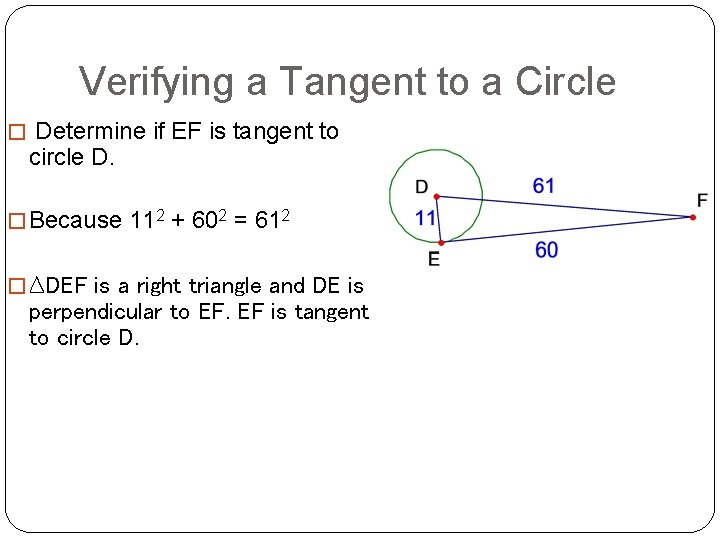
Verifying a Tangent to a Circle � Determine if EF is tangent to circle D. � Because 112 + 602 = 612 � ∆DEF is a right triangle and DE is perpendicular to EF. EF is tangent to circle D.
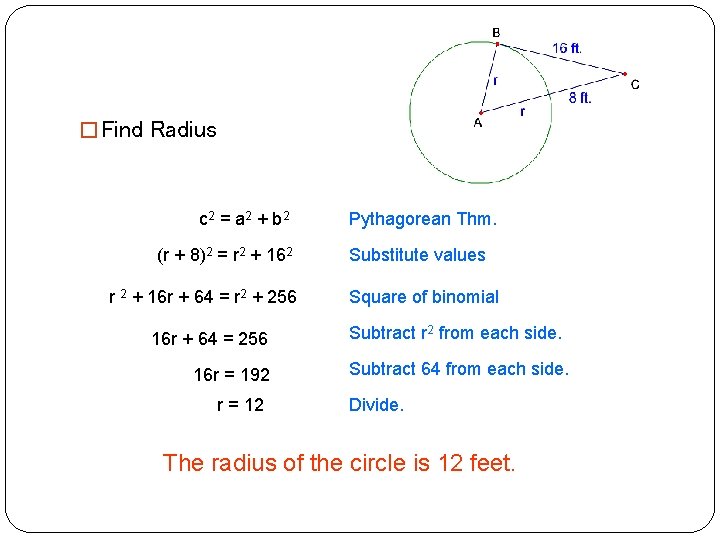
� Find Radius c 2 = a 2 + b 2 (r + 8)2 = r 2 + 162 r 2 + 16 r + 64 = r 2 + 256 16 r + 64 = 256 16 r = 192 r = 12 Pythagorean Thm. Substitute values Square of binomial Subtract r 2 from each side. Subtract 64 from each side. Divide. The radius of the circle is 12 feet.
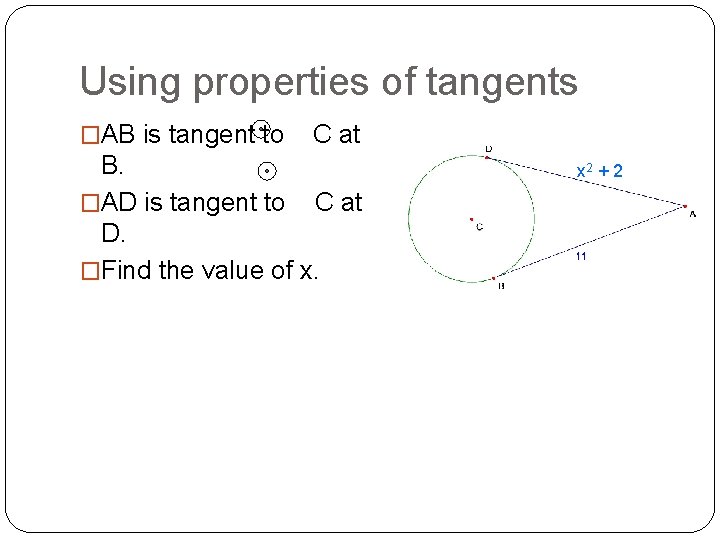
Using properties of tangents �AB is tangent to C at B. �AD is tangent to C at D. �Find the value of x. x 2 + 2

�AB is tangent to C at B. �AD is tangent to C at D. �Find the value of x. x 2 + 2 AB = AD Two tangent segments from the same point are 11 = x 2 + 2 Substitute values 9 = x 2 Subtract 2 from each side. 3=x Find the square root of 9. The value of x is 3 or -3.

Practice
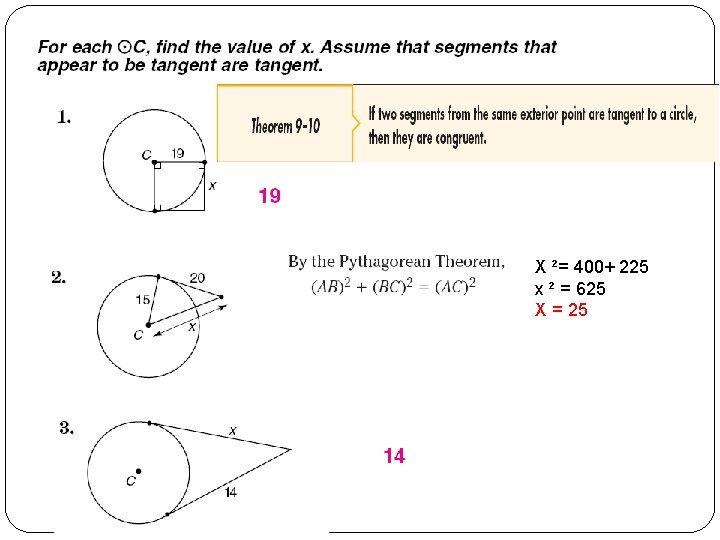
X ²= 400+ 225 x ² = 625 X = 25
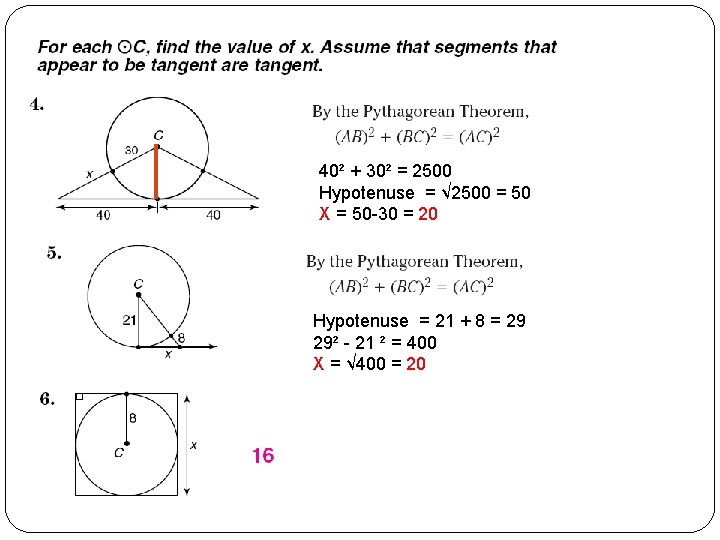
40² + 30² = 2500 Hypotenuse = √ 2500 = 50 X = 50 -30 = 20 Hypotenuse = 21 + 8 = 29 29² - 21 ² = 400 X = √ 400 = 20
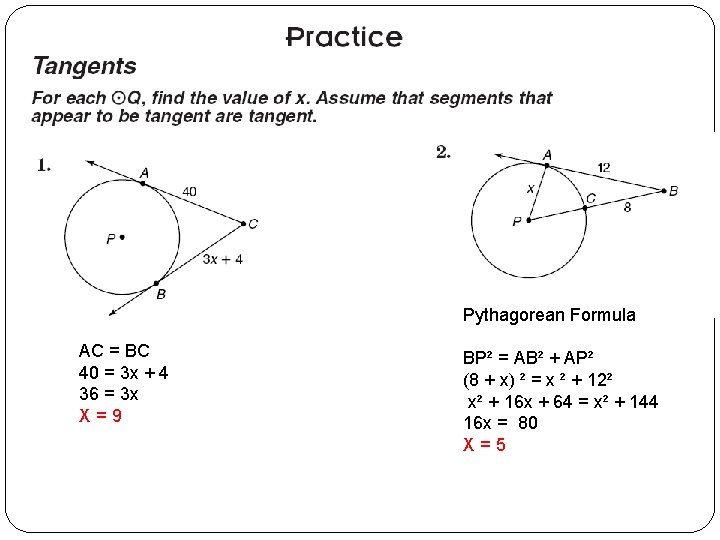
Pythagorean Formula AC = BC 40 = 3 x + 4 36 = 3 x X=9 BP² = AB² + AP² (8 + x) ² = x ² + 12² x² + 16 x + 64 = x² + 144 16 x = 80 X=5
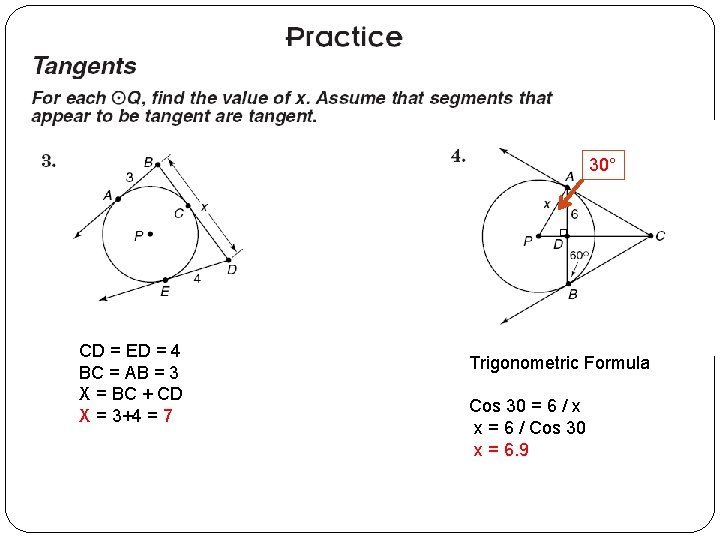
30° CD = ED = 4 BC = AB = 3 X = BC + CD X = 3+4 = 7 Trigonometric Formula Cos 30 = 6 / x x = 6 / Cos 30 x = 6. 9
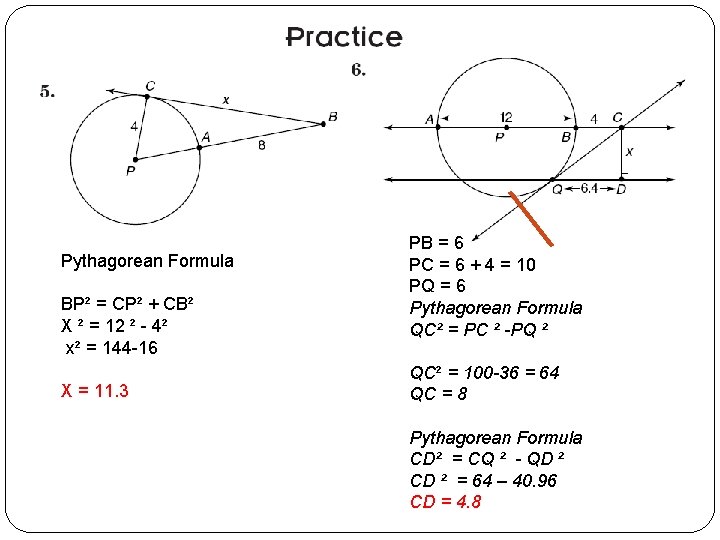
Pythagorean Formula BP² = CP² + CB² X ² = 12 ² - 4² x² = 144 -16 X = 11. 3 PB = 6 PC = 6 + 4 = 10 PQ = 6 Pythagorean Formula QC² = PC ² -PQ ² QC² = 100 -36 = 64 QC = 8 Pythagorean Formula CD² = CQ ² - QD ² CD ² = 64 – 40. 96 CD = 4. 8
- Slides: 24