Secants Tangents and Angle Measures Chapter 10 6

• Find measures of angles formed by lines intersecting on or inside a

Tangent-Chord (or secant) Theorem If a tangent and a chord intersect at a point

A. 122 B. 58 C. 106 D. 116 1. 2. 3. 4. A B

2 -Chord (or Secant) Theorem • If 2 chords intersect in the interior of

A. 42 B. 84 C. 96 D. 138 A. B. C. D. A B

2 -Line Theorem • If 2 lines intersect on the exterior of a circle,

Example: m X = ½ (100 - 40) 100 o m X = ½

Find x. A. 76 B. 73 C. 111 D. 146 1. 2. 3. 4.

JEWELRY A jeweler wants to craft a pendant with the shape shown. Use the

PARKS Two sides of a fence to be built around a circular garden in

Secant-Tangent Angle Find x. 62 = (141 – x) 124 = 141 – x

Homework Chapter 10. 6 • Pg 603 6 – 26, 32 – 34, 55

Slides: 18

Download presentation

Secants, Tangents and Angle Measures Chapter 10 -6

• Find measures of angles formed by lines intersecting on or inside a circle. • Find measures of angles formed by lines intersecting outside the circle. • secant Standard 7. 0 Students prove and use theorems involving the properties of parallel lines cut by a transversal, the properties of quadrilaterals, and the properties of circles. (Key) Standard 21. 0 Students prove and solve problems regarding relationships among chords, secants, tangents, inscribed angles, and inscribed and circumscribed polygons of circles. (Key)

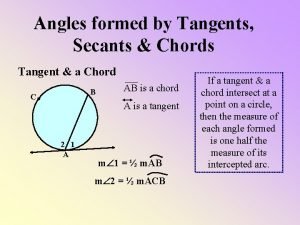
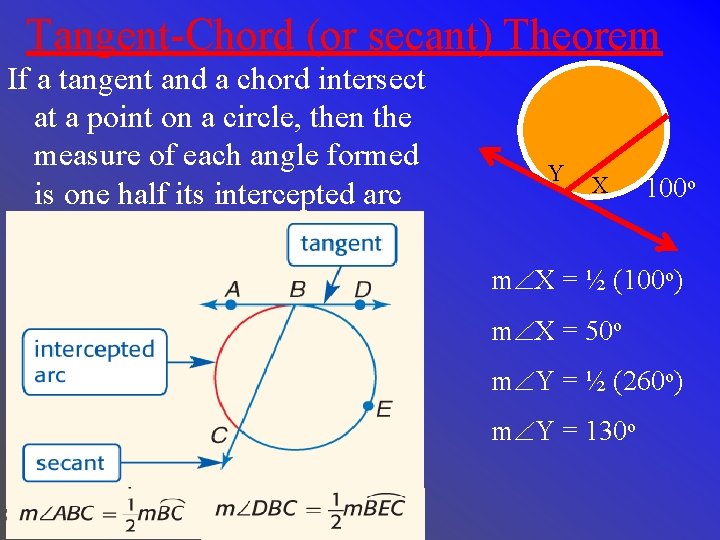
Tangent-Chord (or secant) Theorem If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half its intercepted arc Y X 100 o m X = ½ (100 o) m X = 50 o m Y = ½ (260 o) m Y = 130 o

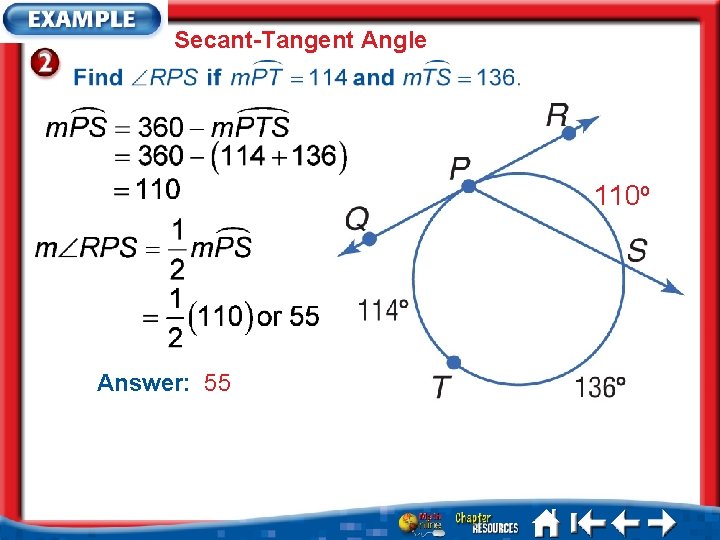
Secant-Tangent Angle 110 o Answer: 55

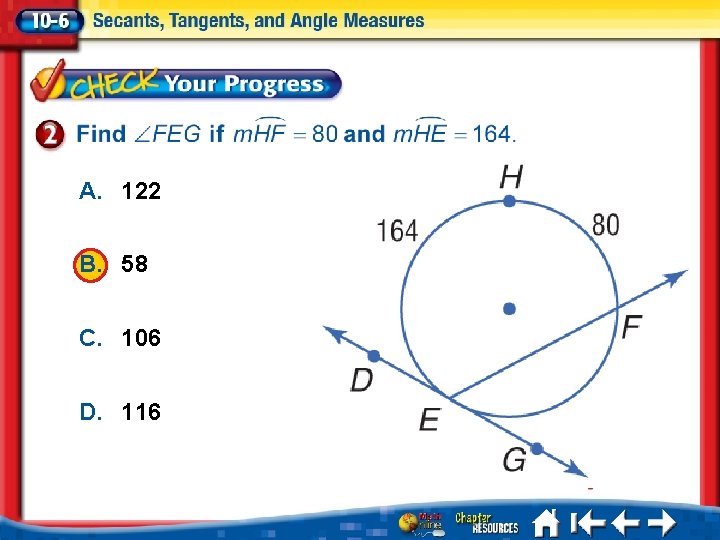
A. 122 B. 58 C. 106 D. 116 1. 2. 3. 4. A B C D

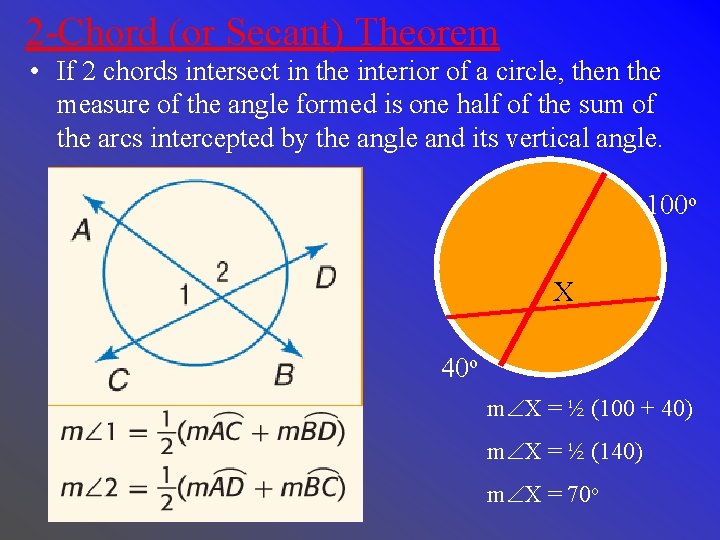
2 -Chord (or Secant) Theorem • If 2 chords intersect in the interior of a circle, then the measure of the angle formed is one half of the sum of the arcs intercepted by the angle and its vertical angle. 100 o X 40 o m X = ½ (100 + 40) m X = ½ (140) m X = 70 o

Secant-Secant Angle Method 1

Secant-Secant Angle Method 2 Answer: 98

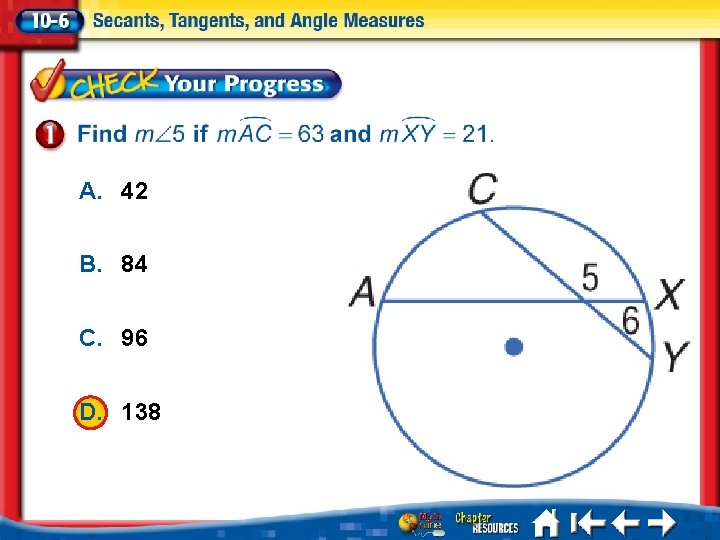
A. 42 B. 84 C. 96 D. 138 A. B. C. D. A B C D

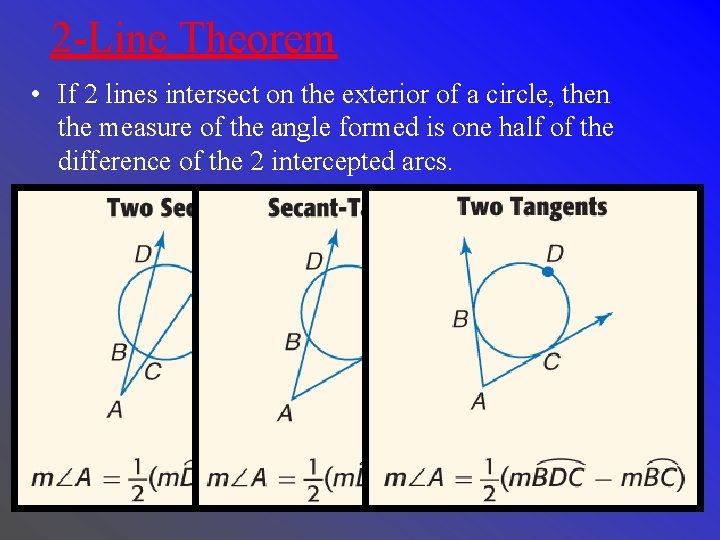
2 -Line Theorem • If 2 lines intersect on the exterior of a circle, then the measure of the angle formed is one half of the difference of the 2 intercepted arcs.

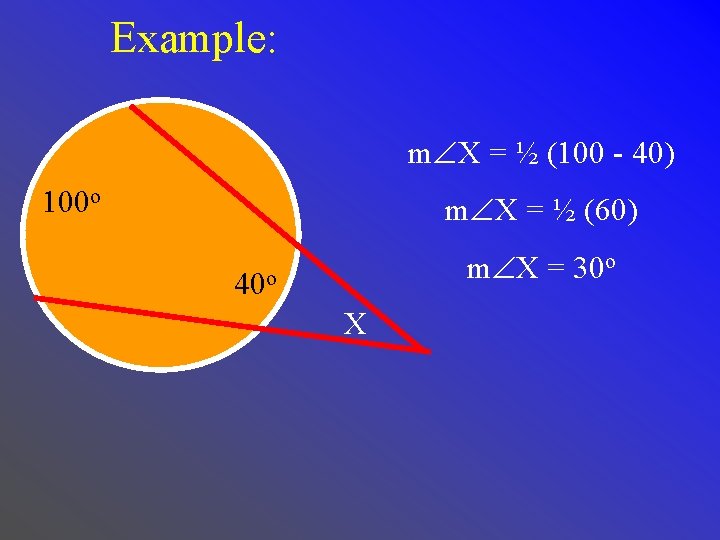
Example: m X = ½ (100 - 40) 100 o m X = ½ (60) m X = 30 o 40 o X

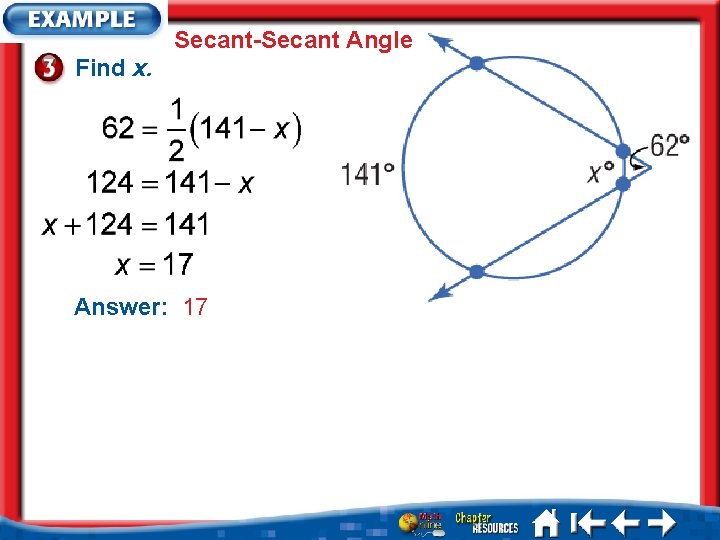
Secant-Secant Angle Find x. Answer: 17

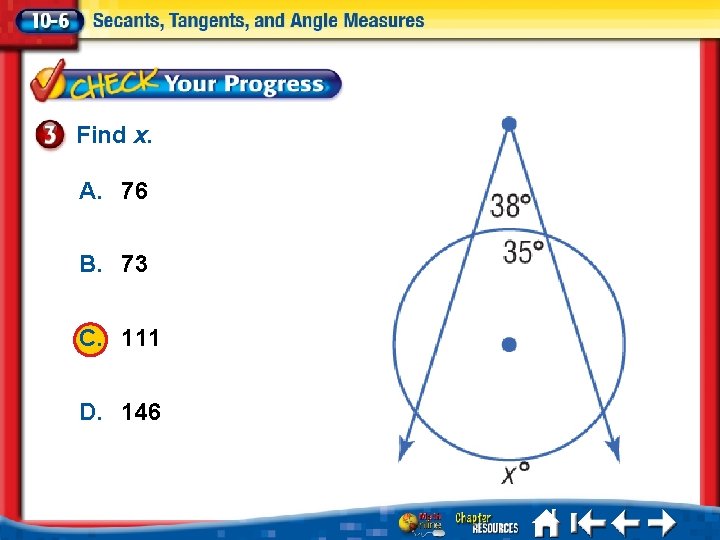
Find x. A. 76 B. 73 C. 111 D. 146 1. 2. 3. 4. A B C D

JEWELRY A jeweler wants to craft a pendant with the shape shown. Use the figure to determine the measure of the arc at the bottom of the pendant. 360 – x Answer: 220 x

PARKS Two sides of a fence to be built around a circular garden in a park are shown. Use the figure to determine the measure of A. A. 75 B. 127. 5 C. 105 D. 52. 5 A. B. C. D. A B C D

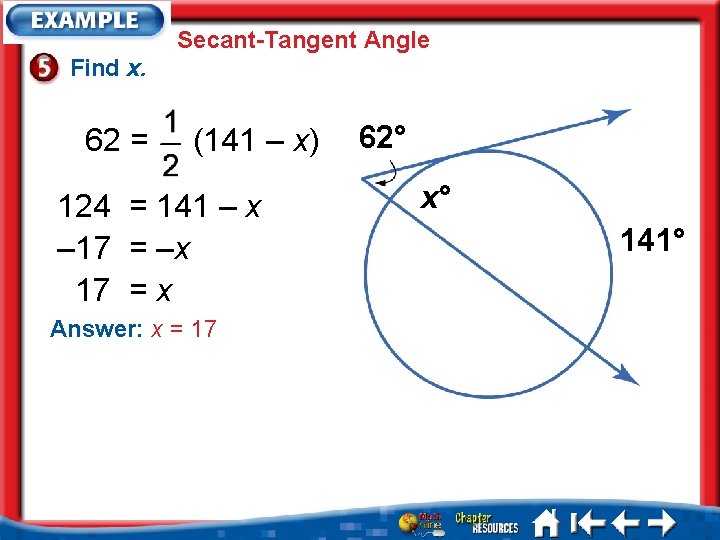
Secant-Tangent Angle Find x. 62 = (141 – x) 124 = 141 – x – 17 = –x 17 = x Answer: x = 17 62° x° 141°

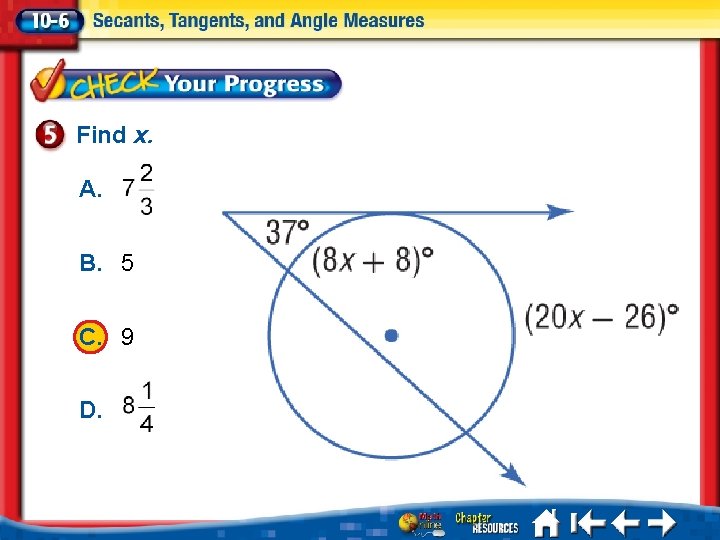
Find x. A. B. 5 C. 9 D. A. B. C. D. A B C D

Homework Chapter 10. 6 • Pg 603 6 – 26, 32 – 34, 55 – 57