FiveMinute Check over Lesson 10 4 NGSSS ThenNow

Five-Minute Check (over Lesson 10– 4) NGSSS Then/Now New Vocabulary Example 1: Identify Common Tangents Theorem 10. 10 Example 2: Identify a Tangent Example 3: Use a Tangent to Find Missing Values Theorem 10. 11 Example 4: Use Congruent Tangents to Find Measures Example 5: Real-World Example: Find Measures in Circimscribed Polygons

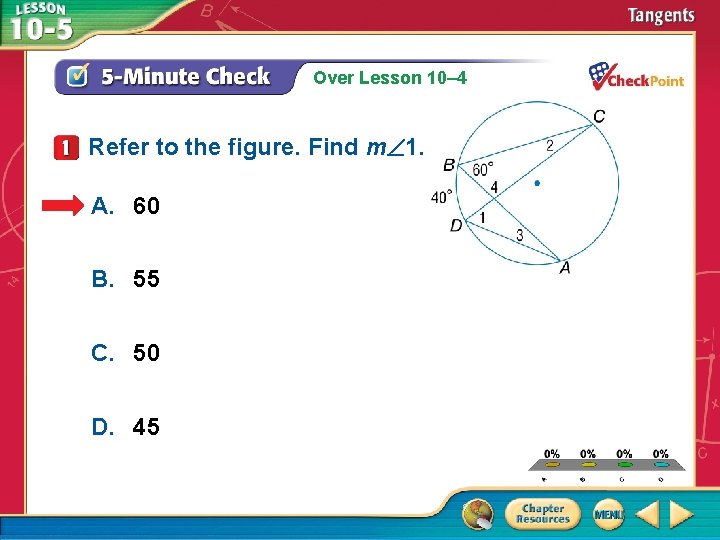
Over Lesson 10– 4 Refer to the figure. Find m 1. A. 60 B. 55 C. 50 D. 45 A. B. C. D. A B C D

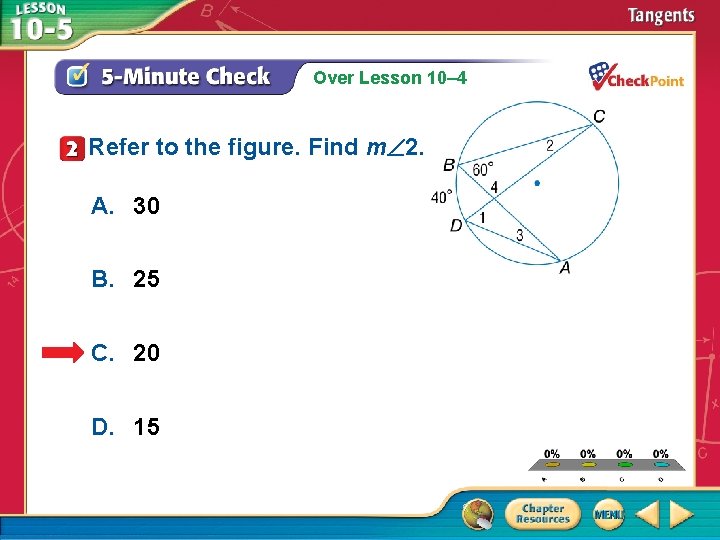
Over Lesson 10– 4 Refer to the figure. Find m 2. A. 30 B. 25 C. 20 D. 15 A. B. C. D. A B C D

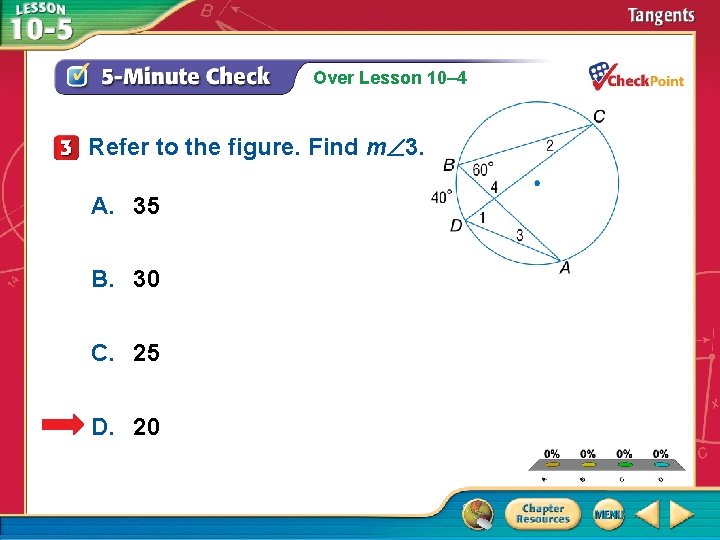
Over Lesson 10– 4 Refer to the figure. Find m 3. A. 35 B. 30 C. 25 D. 20 A. B. C. D. A B C D

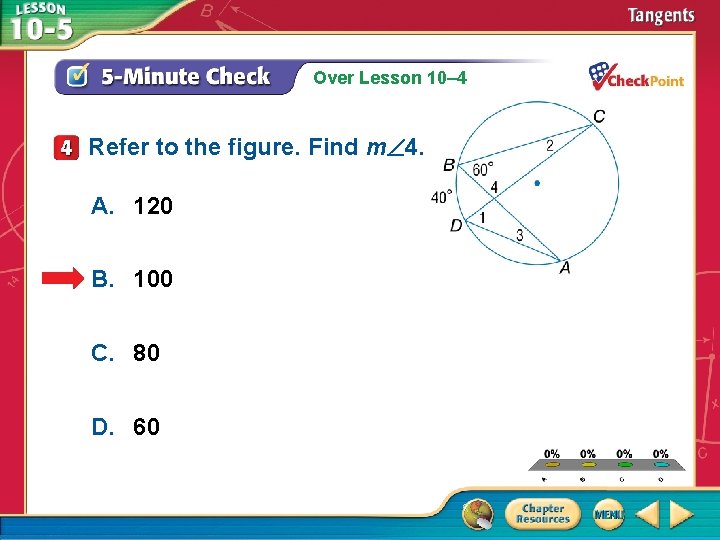
Over Lesson 10– 4 Refer to the figure. Find m 4. A. 120 B. 100 C. 80 D. 60 A. B. C. D. A B C D

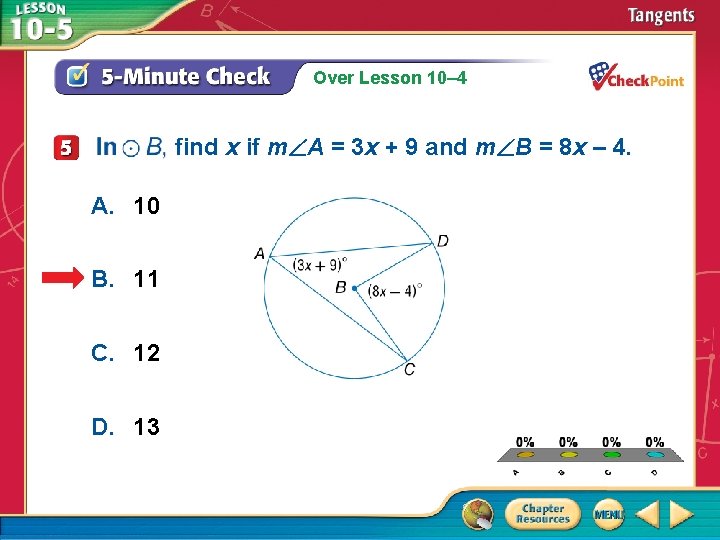
Over Lesson 10– 4 find x if m A = 3 x + 9 and m B = 8 x – 4. A. 10 B. 11 C. 12 D. 13 A. B. C. D. A B C D

Over Lesson 10– 4 The measure of an arc is 95°. What is the measure of an inscribed angle that intercepts it? A. 47. 5° B. 95° C. 190° D. 265° A. B. C. D. A B C D

MA. 912. G. 6. 1 Determine the center of a given circle. Given three points not on a line, construct the circle that passes through them. Construct tangents to circles. Circumscribe and inscribe circles about and within triangles and regular polygons. MA. 912. G. 6. 4 Determine and use measures of arcs and related angles. Also addresses MA. 912. G. 6. 2 and MA. 912. G. 6. 3.

You used the Pythagorean Theorem to find side lengths of right triangles. (Lesson 8– 2) • Use properties of tangents. • Solve problems involving circumscribed polygons.

• tangent • point of tangency • common tangent

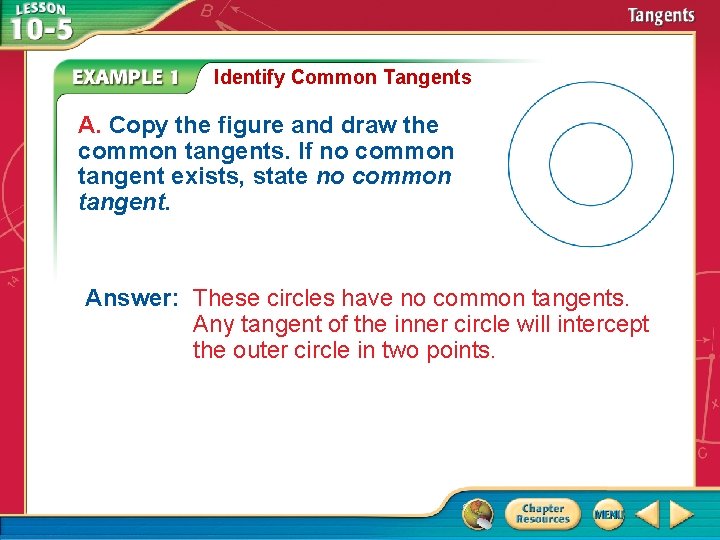
Identify Common Tangents A. Copy the figure and draw the common tangents. If no common tangent exists, state no common tangent. Answer: These circles have no common tangents. Any tangent of the inner circle will intercept the outer circle in two points.

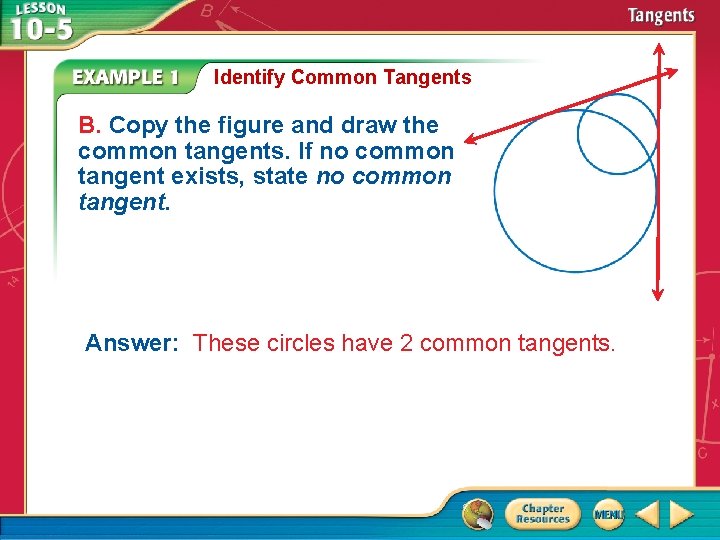
Identify Common Tangents B. Copy the figure and draw the common tangents. If no common tangent exists, state no common tangent. Answer: These circles have 2 common tangents.

A. Copy the figure and draw the common tangents to determine how many there are. If no common tangent exists, choose no common tangent. A. 2 common tangents B. 4 common tangents C. 6 common tangents D. no common tangents A. B. C. D. A B C D

B. Copy the figure and draw the common tangents to determine how many there are. If no common tangent exists, choose no common tangent. A. 2 common tangents B. 3 common tangents C. 4 common tangents D. no common tangents A. B. C. D. A B C D

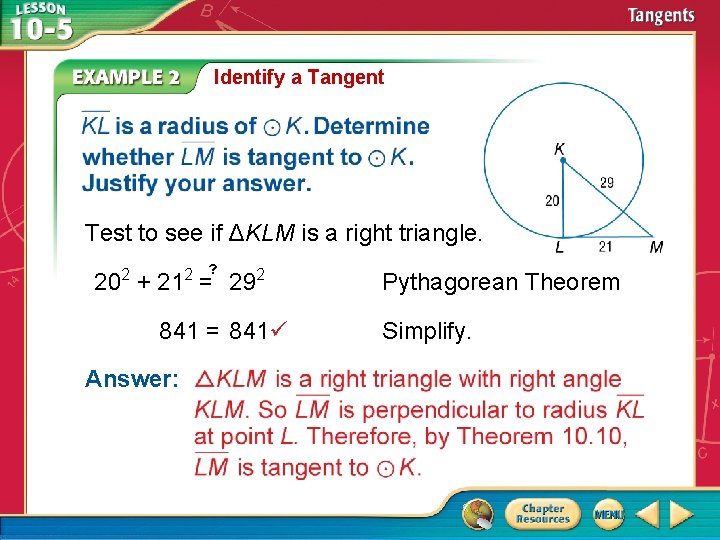
Identify a Tangent Test to see if ΔKLM is a right triangle. 2 2 ? 20 + 21 = 292 841 = 841 Answer: Pythagorean Theorem Simplify.

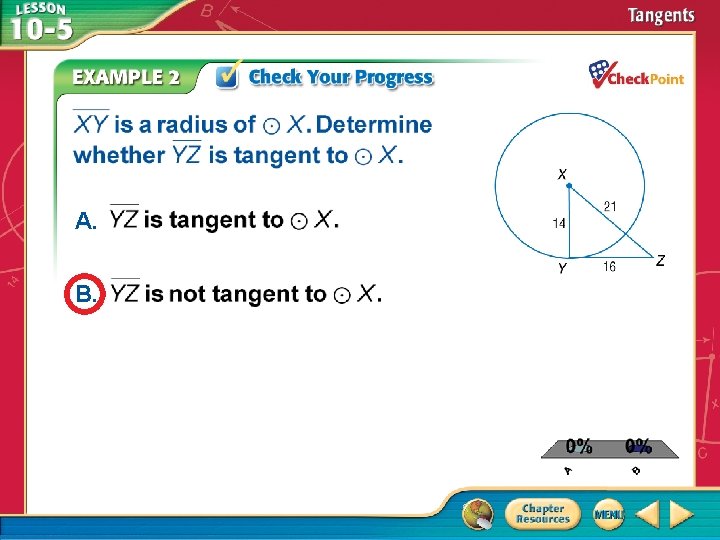
A. B. A. A B. B

Use a Tangent to Find Missing Values EW 2 + DW 2 = DE 2 Pythagorean Theorem 242 + x 2 = (x + 16)2 EW = 24, DW = x, and DE = x + 16 576 + x 2 = x 2 + 32 x + 256 Multiply. 320 = 32 x 10 = x Answer: x = 10 Simplify. Divide each side by 32.

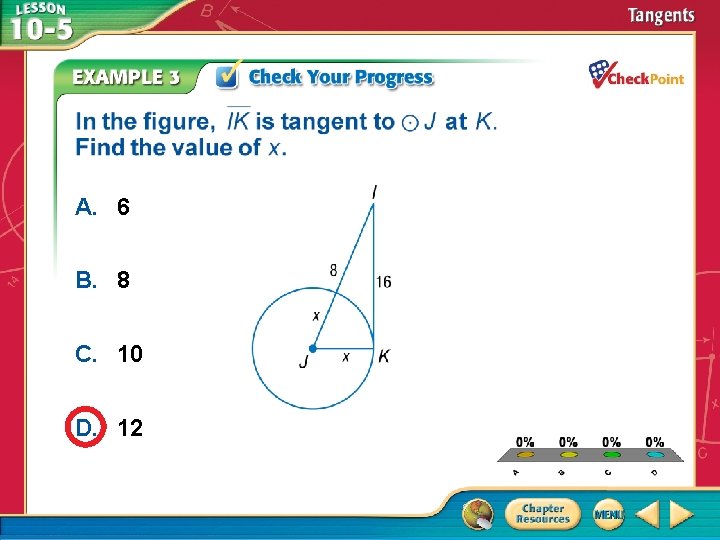
A. 6 B. 8 C. 10 D. 12 A. B. C. D. A B C D

Use Congruent Tangents to Find Measures AC = BC 3 x + 2 = 4 x – 3 Tangents from the same exterior point are congruent. Substitution 2= x– 3 Subtract 3 x from each side. 5= x Add 3 to each side. Answer: x = 5

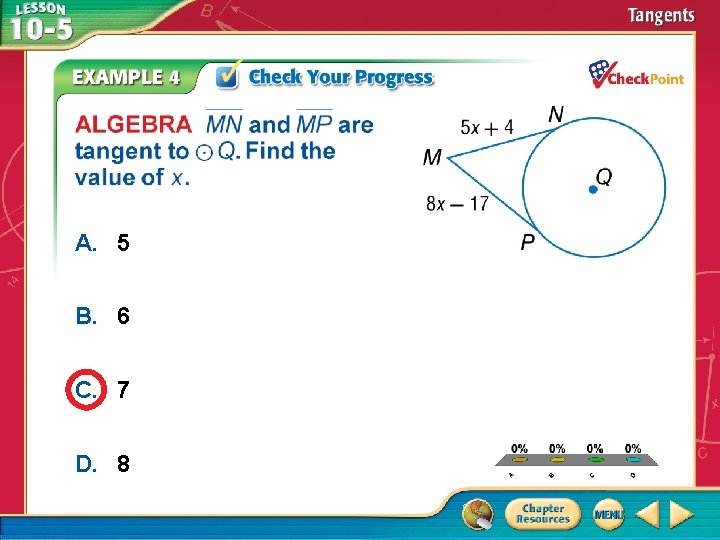
A. 5 B. 6 C. 7 D. 8 A. B. C. D. A B C D

Find Measures in Circumscribed Polygons Step 1 Find the missing measures.

Find Measures in Circumscribed Polygons Step 2 Find the perimeter of ΔQRS. = 10 + 2 + 8 + 6 + 10 or 36 cm Answer: So, the perimeter of ΔQRS is 36 cm.

A. 42 cm B. 44 cm C. 48 cm D. 56 cm A. B. C. D. A B C D