ESCOLHA A AULA TEMA FRMULAS Prof Marcio Sandron

ESCOLHA A AULA TEMA FÓRMULAS: Prof. Marcio Sandron

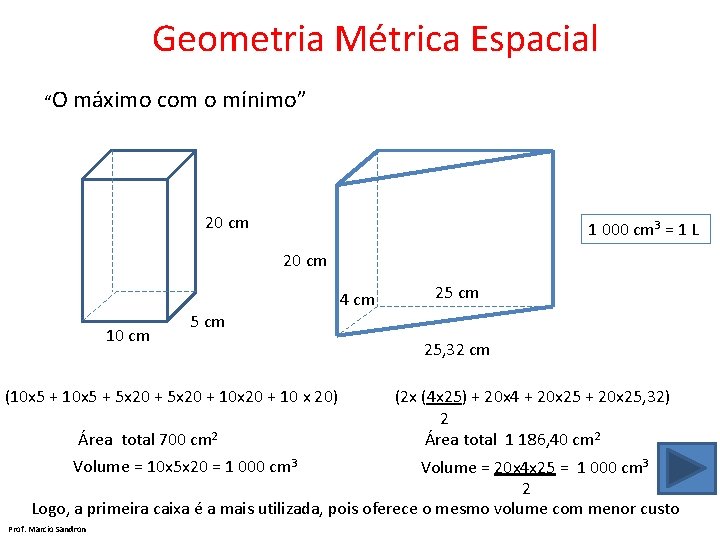
Geometria Métrica Espacial “O máximo com o mínimo” 20 cm 1 000 cm 3 = 1 L 20 cm 4 cm 10 cm 25 cm (10 x 5 + 5 x 20 + 10 x 20 + 10 x 20) Área total 700 cm 2 Volume = 10 x 5 x 20 = 1 000 cm 3 25, 32 cm (2 x (4 x 25) + 20 x 4 + 20 x 25, 32) 2 Área total 1 186, 40 cm 2 Volume = 20 x 4 x 25 = 1 000 cm 3 2 Logo, a primeira caixa é a mais utilizada, pois oferece o mesmo volume com menor custo Prof. Marcio Sandron

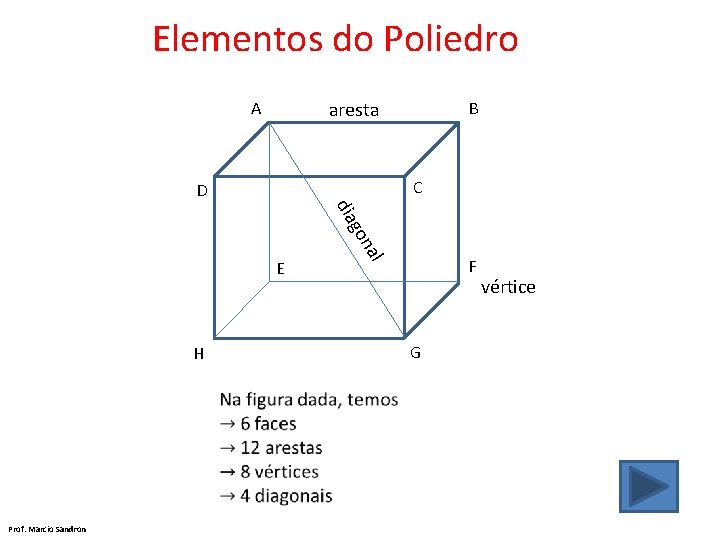
Elementos do Poliedro aresta A B C D go dia l F G H Prof. Marcio Sandron na E vértice

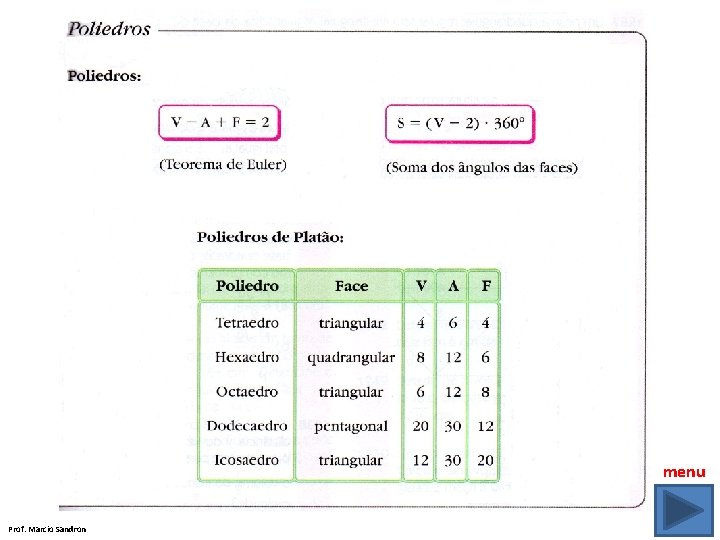
Nomenclatura dos Poliedro Um poliedro convexo é regular se suas faces são polígonos regulares com o mesmo número De lados e em cada vértice converge o mesmo número de arestas. Existem apenas cinco tipos de poliedros regulares: Tetraedro, Octaedro, Icosaedro, Hexaedro e Dodecaedro Prof. Marcio Sandron

Relação de EULER V + F = A + 2 Exemplo: Um poliedro possui 4 faces triangulares e 3 faces hexagonais. Determine o número de arestas e de vértices desse poliedro. Número de vértices: V + F = A + 2 V + 7 = 15 + 2 V = 17 – 7 V = 10 Resp: O poliedro possui 7 faces, 15 arestas e 10 vértices Prof. Marcio Sandron

9 vértices 6 faces 14 arestas 8 faces 15 arestas e 8 vértices menu 13 vértices Prof. Marcio Sandron

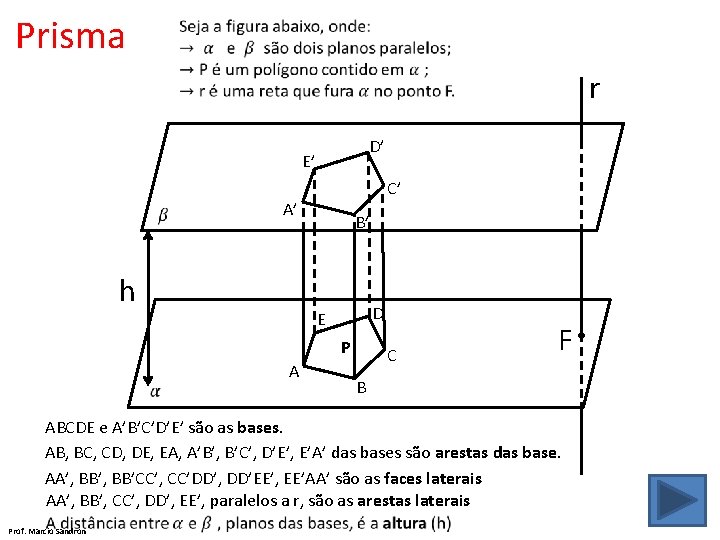
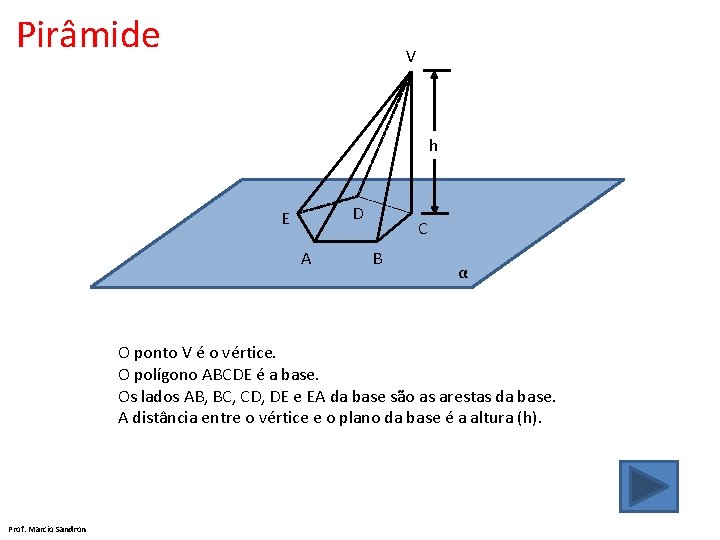
Prisma r D’ E’ C’ A’ h B’ D E P A C F B ABCDE e A’B’C’D’E’ são as bases. AB, BC, CD, DE, EA, A’B’, B’C’, D’E’, E’A’ das bases são arestas das base. AA’, BB’CC’, CC’DD’, DD’EE’, EE’AA’ são as faces laterais AA’, BB’, CC’, DD’, EE’, paralelos a r, são as arestas laterais Prof. Marcio Sandron

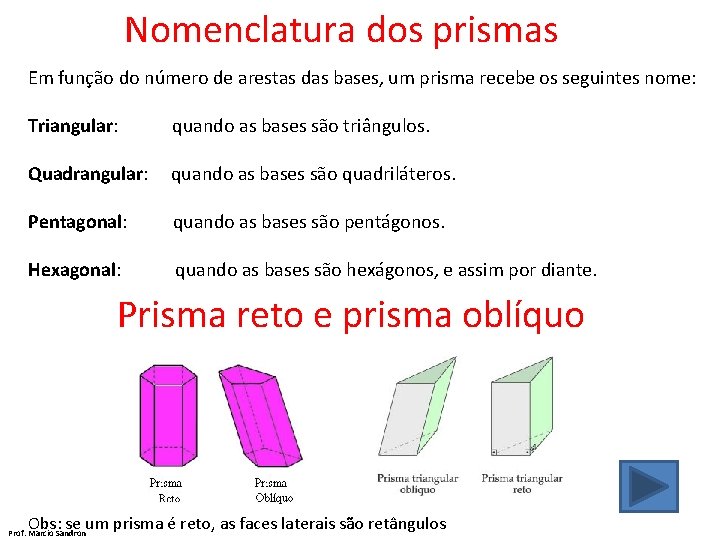
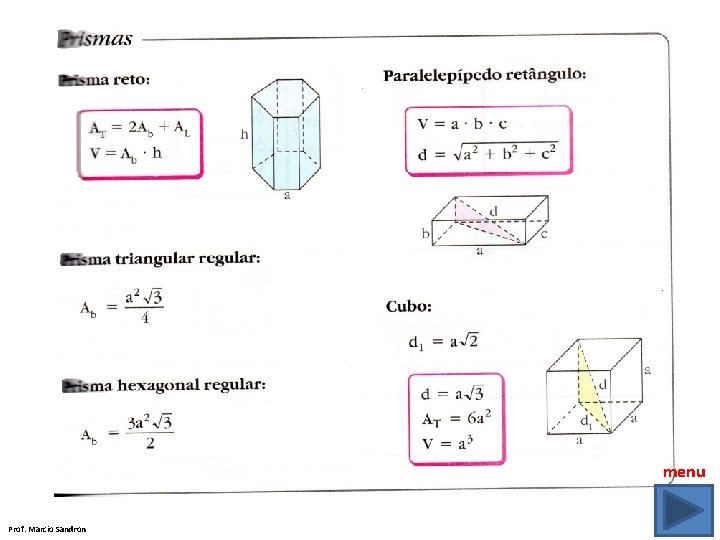
Nomenclatura dos prismas Em função do número de arestas das bases, um prisma recebe os seguintes nome: Triangular: quando as bases são triângulos. Quadrangular: quando as bases são quadriláteros. Pentagonal: quando as bases são pentágonos. Hexagonal: quando as bases são hexágonos, e assim por diante. Prisma reto e prisma oblíquo Obs: se um prisma é reto, as faces laterais são retângulos Prof. Marcio Sandron

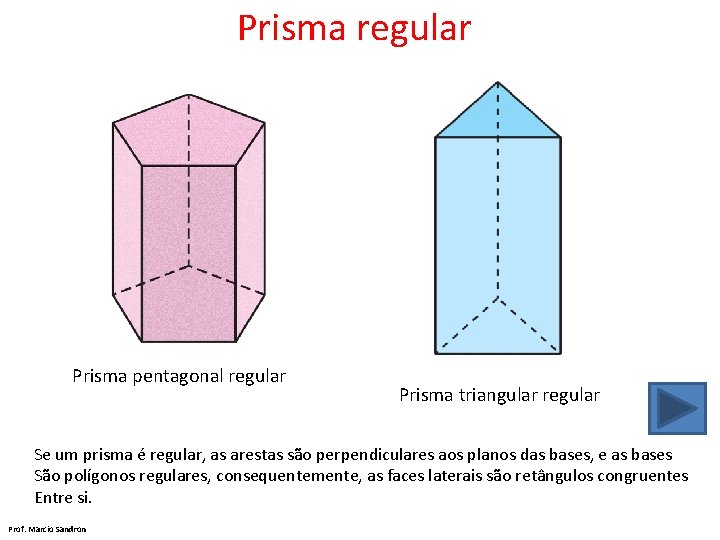
Prisma regular Prisma pentagonal regular Prisma triangular regular Se um prisma é regular, as arestas são perpendiculares aos planos das bases, e as bases São polígonos regulares, consequentemente, as faces laterais são retângulos congruentes Entre si. Prof. Marcio Sandron

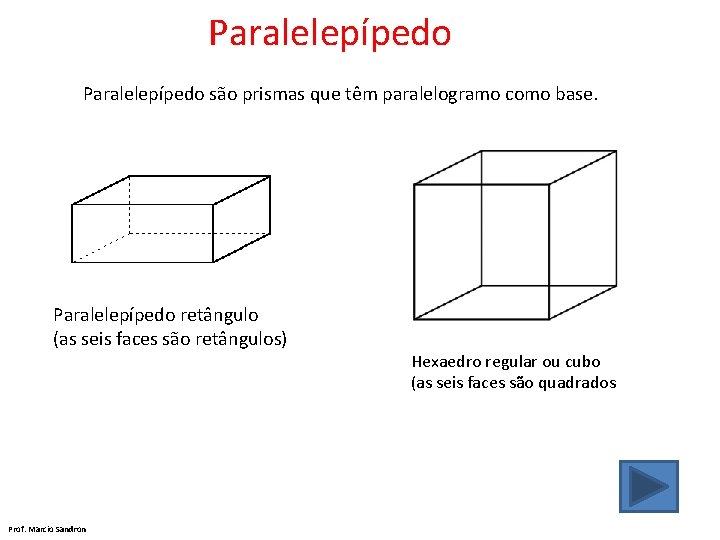
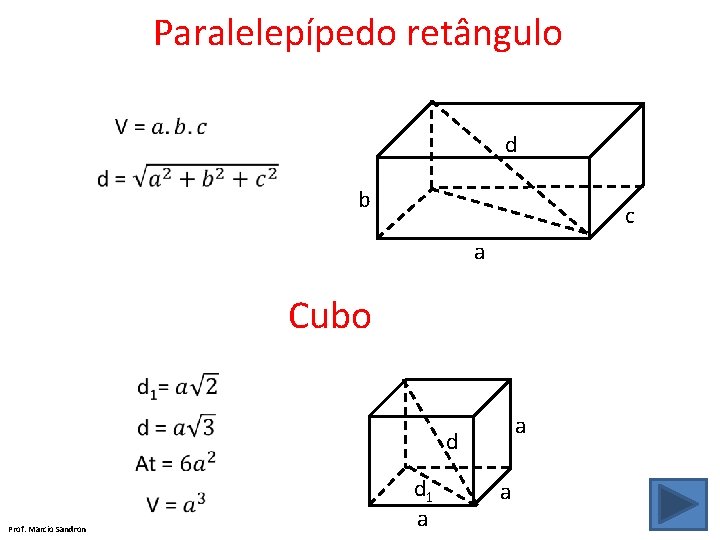
Paralelepípedo são prismas que têm paralelogramo como base. Paralelepípedo retângulo (as seis faces são retângulos) Prof. Marcio Sandron Hexaedro regular ou cubo (as seis faces são quadrados

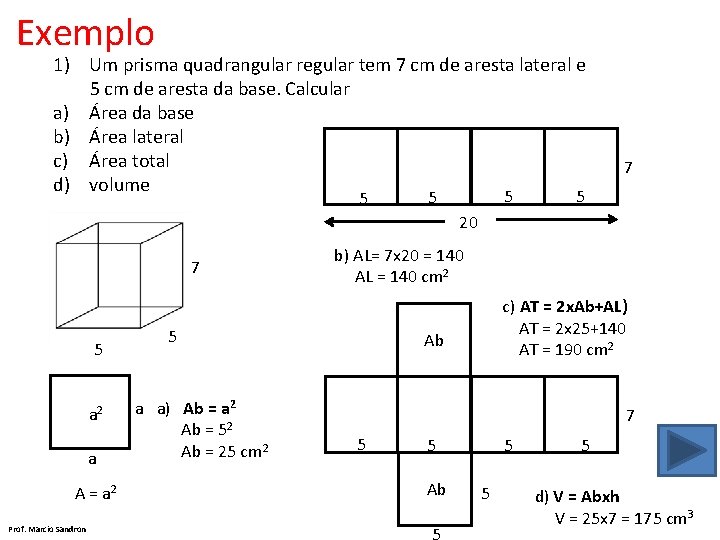
Exemplo 1) Um prisma quadrangular regular tem 7 cm de aresta lateral e 5 cm de aresta da base. Calcular a) Área da base b) Área lateral c) Área total d) volume 5 5 5 7 5 20 7 5 a 2 a A = a 2 Prof. Marcio Sandron b) AL= 7 x 20 = 140 AL = 140 cm 2 5 a a) Ab = a 2 Ab = 52 Ab = 25 cm 2 c) AT = 2 x. Ab+AL) AT = 2 x 25+140 AT = 190 cm 2 Ab 7 5 5 Ab 5 5 5 d) V = Abxh V = 25 x 7 = 175 cm 3

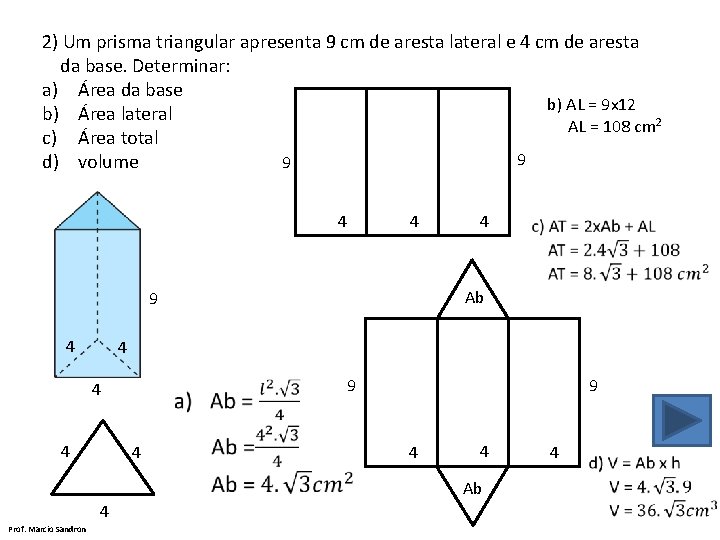
2) Um prisma triangular apresenta 9 cm de aresta lateral e 4 cm de aresta da base. Determinar: a) Área da base b) AL = 9 x 12 b) Área lateral AL = 108 cm 2 c) Área total 9 d) volume 9 4 4 4 9 9 4 4 Ab 4 Prof. Marcio Sandron Ab 9 4 4 4

Paralelepípedo retângulo d b c a Cubo d Prof. Marcio Sandron a d 1 a a

Exemplo 1) Num paralelepípedo reto-retângulo de dimensões 5 cm, 4 cm e 3 cm, calcule: a) A diagonal b) A área total c) O volume d 3 cm 5 cm 2) Se a área total de um cubo é 24 cm 2, calcule: a) A aresta b) O volume Prof. Marcio Sandron 4 cm

Exercícios Propostos: 1) Calcule a diagonal, a área total e o volume de um paralelepípedo reto-retângulo de dimensões 8 cm, 6 cm e 4 cm. 2) A base de um paralelepípedo reto-retângulo é um quadrado de área 36 cm 2. Calcule a diagonal, a área total e o volume desse paralelepípedo sabendo-se que sua altura é igual a 4 cm. 3) A base de um paralelepípedo reto-retângulo é um quadrado. Calcule o volume desse paralelepípedo sabendo-se que sua altura é igual a 3 cm e sua área total é igual a 80 cm 2. 4) Calcule a diagonal, a área total e o volume de um cubo de aresta igual a 5 cm. 5) Calcule a aresta e o volume de um cubo cuja área total é igual a 96 cm 2. menu Prof. Marcio Sandron

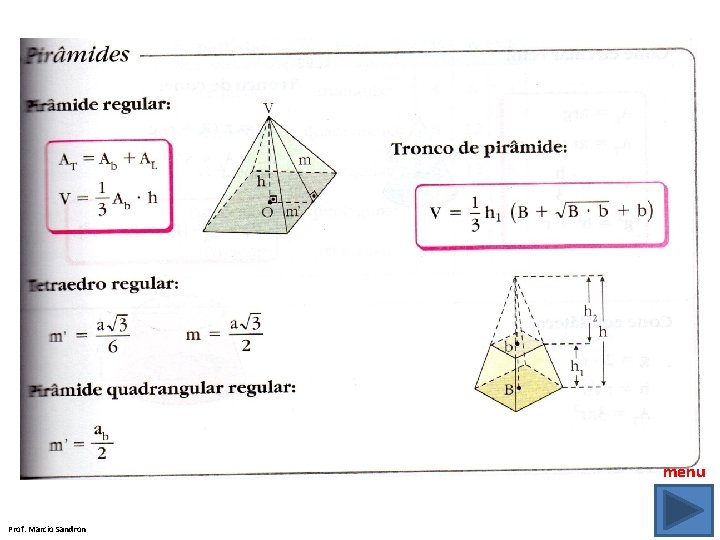
Pirâmide V h D E A C B α O ponto V é o vértice. O polígono ABCDE é a base. Os lados AB, BC, CD, DE e EA da base são as arestas da base. A distância entre o vértice e o plano da base é a altura (h). Prof. Marcio Sandron

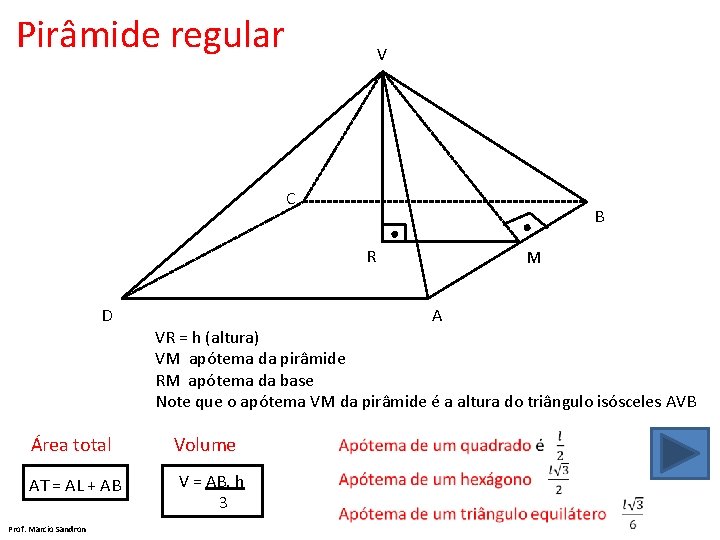
Pirâmide regular V C B R D A VR = h (altura) VM apótema da pirâmide RM apótema da base Note que o apótema VM da pirâmide é a altura do triângulo isósceles AVB Área total Volume AT = AL + AB V = AB. h 3 Prof. Marcio Sandron M

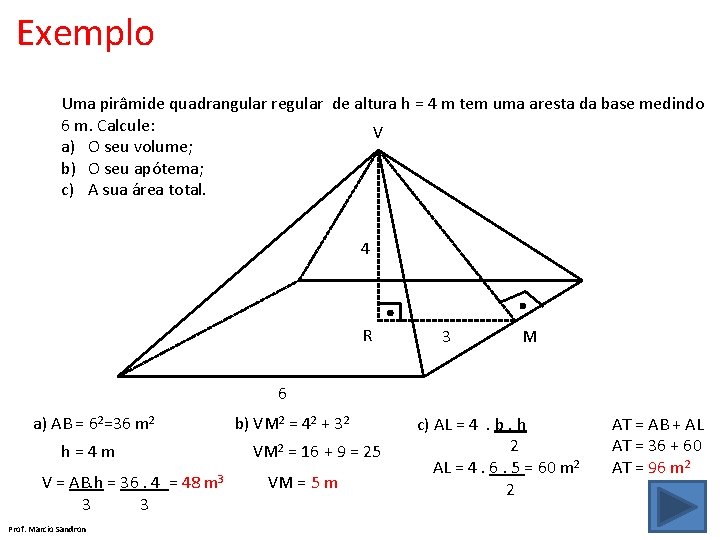
Exemplo Uma pirâmide quadrangular regular de altura h = 4 m tem uma aresta da base medindo 6 m. Calcule: V a) O seu volume; b) O seu apótema; c) A sua área total. 4 R 3 M 6 a) AB = 62=36 m 2 h = 4 m V = AB. h = 36. 4 = 48 m 3 3 3 Prof. Marcio Sandron b) VM 2 = 42 + 32 VM 2 = 16 + 9 = 25 VM = 5 m c) AL = 4 . b. h 2 AL = 4. 6. 5 = 60 m 2 AT = AB + AL AT = 36 + 60 AT = 96 m 2

AT = 576 cm 2 e V=512 cm 3 AT = 360 cm 2 e V=400 cm 3 Prof. Marcio Sandron menu

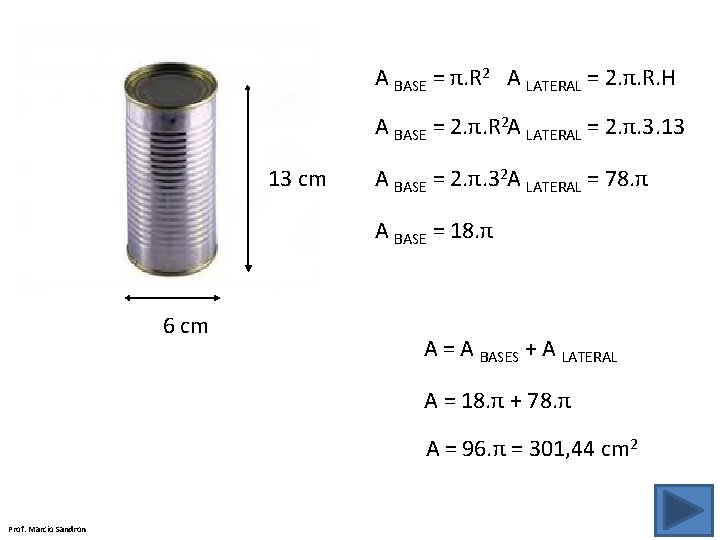
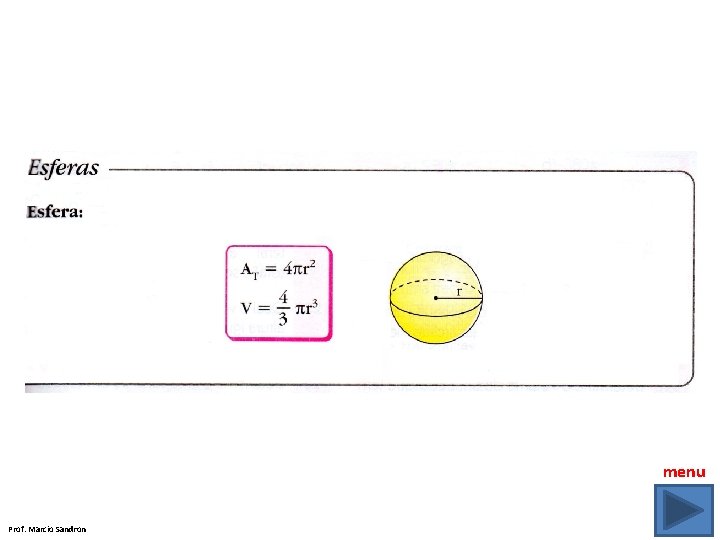
ÁREA DA SUPERFÍCIE DE UM CILINDRO BASE H (ALTURA) BASE Prof. Marcio Sandron

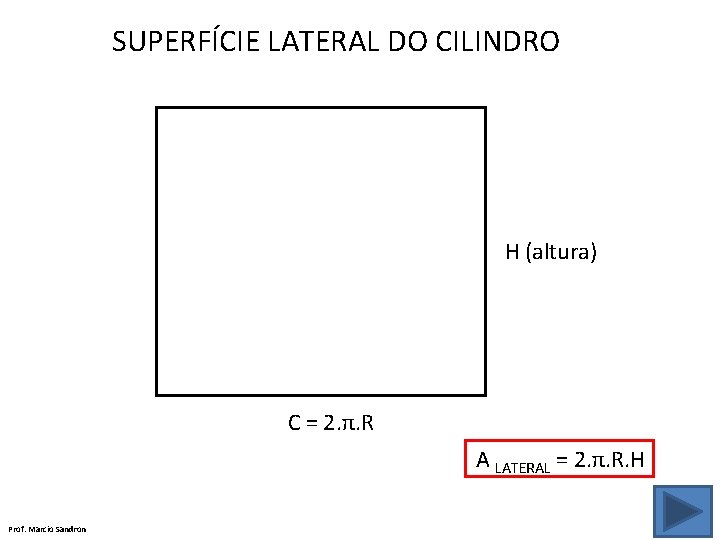
SUPERFÍCIE LATERAL DO CILINDRO H (altura) C = 2. π. R A LATERAL = 2. π. R. H Prof. Marcio Sandron

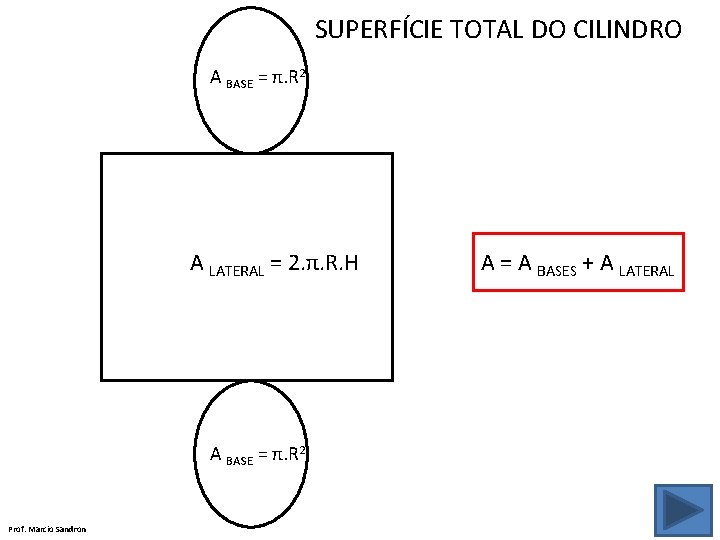
SUPERFÍCIE TOTAL DO CILINDRO A BASE = π. R 2 A LATERAL = 2. π. R. H A BASE = π. R 2 Prof. Marcio Sandron A = A BASES + A LATERAL

A BASE = π. R 2 A LATERAL = 2. π. R. H A BASE = 2. π. R 2 A LATERAL = 2. π. 3. 13 13 cm A BASE = 2. π. 32 A LATERAL = 78. π A BASE = 18. π 6 cm A = A BASES + A LATERAL A = 18. π + 78. π A = 96. π = 301, 44 cm 2 Prof. Marcio Sandron

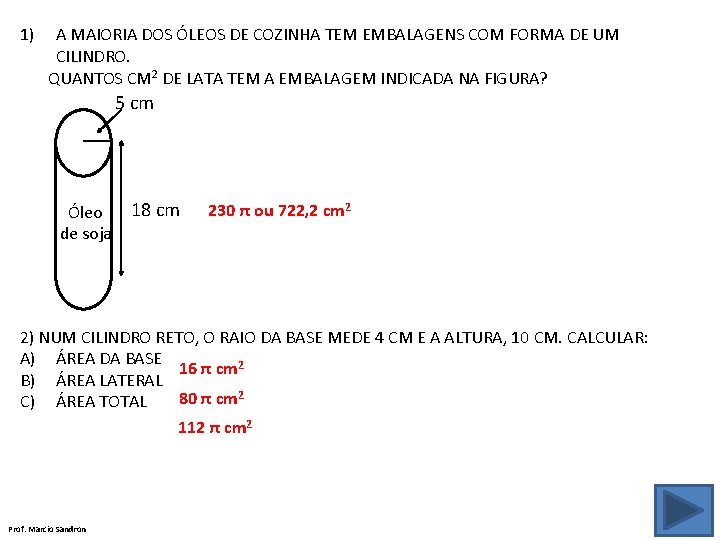
1) A MAIORIA DOS ÓLEOS DE COZINHA TEM EMBALAGENS COM FORMA DE UM CILINDRO. QUANTOS CM 2 DE LATA TEM A EMBALAGEM INDICADA NA FIGURA? 5 cm Óleo de soja 18 cm 230 π ou 722, 2 cm 2 2) NUM CILINDRO RETO, O RAIO DA BASE MEDE 4 CM E A ALTURA, 10 CM. CALCULAR: A) ÁREA DA BASE 16 π cm 2 B) ÁREA LATERAL 80 π cm 2 C) ÁREA TOTAL 112 π cm 2 Prof. Marcio Sandron

VOLUME DO CILINDRO V = ABASE. H V = π. R 2. H H (CAMADAS) 1 cm 3 = 1 ml ml = mililitros Prof. Marcio Sandron

V = ABASE. H H = 9 cm V = π. R 2. H V = 3, 14. 3, 52. 9 R = 3, 5 cm V = 346, 2 cm 3 1 cm 3 = 1 ml V = 346, 2 ml Prof. Marcio Sandron

Para construir uma piscina, foi cavado um buraco cilíndrico de 4 m de Diâmetro por 2, 5 m de profundidade. Vamos calcular o volume de Terra retirado do buraco. V = π. R 2. H D = 2. R V = 3, 14. 22. 2, 5 4 = 2. R V = 3, 14. 22. 2, 5 R = 2 V = 31, 4 m 3 de terra Prof. Marcio Sandron

1)Qual é a quantidade de água necessária para encher completamente o reservatório cujas medidas interiores estão indicadas na figura? 3, 5 m 10, 99 m 3 2 m 2)Paulo poderá guardar meio litro de leite num recipiente cilíndrico com 4 cm de raio e 10 cm de altura? Apresente os cálculos 4 cm Leite 10 cm Sim, porque V= 0, 5024 L > 0, 5 L 3) Num cilindro reto, o raio da base mede 4 cm e a altura, 10 cm, calcular: a) área da base b) área lateral c) área total d) volume 2 16 π cm Prof. Marcio Sandron 80 π cm 2 112 π cm 2 160 π cm 3

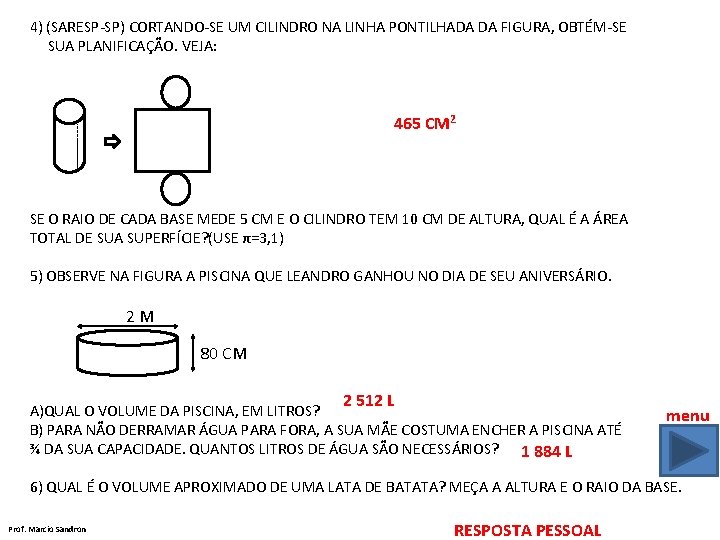
4) (SARESP-SP) CORTANDO-SE UM CILINDRO NA LINHA PONTILHADA DA FIGURA, OBTÉM-SE SUA PLANIFICAÇÃO. VEJA: 465 CM 2 SE O RAIO DE CADA BASE MEDE 5 CM E O CILINDRO TEM 10 CM DE ALTURA, QUAL É A ÁREA TOTAL DE SUA SUPERFÍCIE? (USE π=3, 1) 5) OBSERVE NA FIGURA A PISCINA QUE LEANDRO GANHOU NO DIA DE SEU ANIVERSÁRIO. 2 M 80 CM 2 512 L A)QUAL O VOLUME DA PISCINA, EM LITROS? B) PARA NÃO DERRAMAR ÁGUA PARA FORA, A SUA MÃE COSTUMA ENCHER A PISCINA ATÉ ¾ DA SUA CAPACIDADE. QUANTOS LITROS DE ÁGUA SÃO NECESSÁRIOS? 1 884 L menu 6) QUAL É O VOLUME APROXIMADO DE UMA LATA DE BATATA? MEÇA A ALTURA E O RAIO DA BASE. Prof. Marcio Sandron RESPOSTA PESSOAL

menu Prof. Marcio Sandron

menu Prof. Marcio Sandron

menu Prof. Marcio Sandron

menu Prof. Marcio Sandron

menu Prof. Marcio Sandron

menu Prof. Marcio Sandron