Error Control Codes Detection Correction TsungChu Huang National

Error Control Codes -- Detection & Correction Tsung-Chu Huang National Changhua University of Education 2014/04/12 1

Outline n Motivation and Introduction Ø Communication Channels Ø Storage as Channels n Metrics: Ø Code Rate, Information Rate, Capacity Ø Hamming Distance and Cartesian Distance n Categories: Ø Complex Codes and Simple Codes Ø Linear Codes and Non-Linear Codes Ø Block Codes, Cyclic Codes and Convolution Codes n Self-Check Codes: Ø Berger Codes and Equal-Weight Codes, 3 -8 Codes n n Hamming Codes and BCH Codes Reed Muller Codes and Reed Solomon Codes Turbo Codes Analog Codes: DFT Codes and DCT Codes 2

Classification n 3

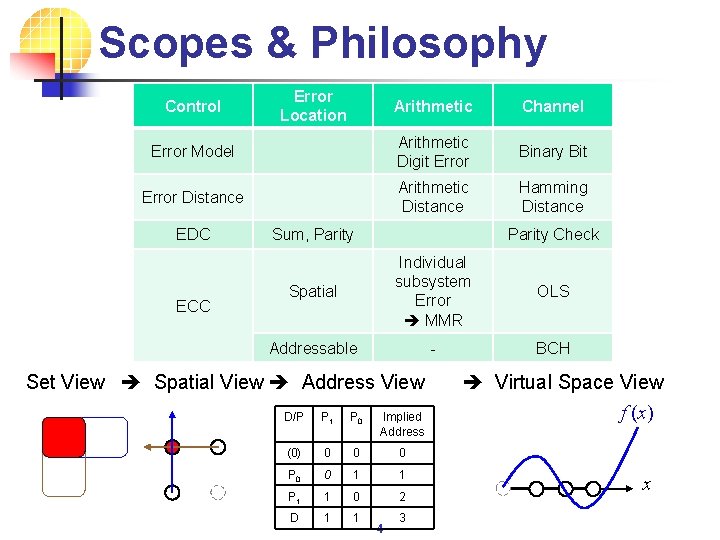
Scopes & Philosophy Control Error Location Arithmetic Channel Error Model Arithmetic Digit Error Binary Bit Error Distance Arithmetic Distance Hamming Distance EDC ECC Sum, Parity Check Spatial Individual subsystem Error MMR OLS Addressable - BCH Set View Spatial View Address View Virtual Space View f (x) D/P P P Implied 1 0 Address (0) 0 0 0 P 0 0 1 1 P 1 1 0 2 D 1 1 4 3 x

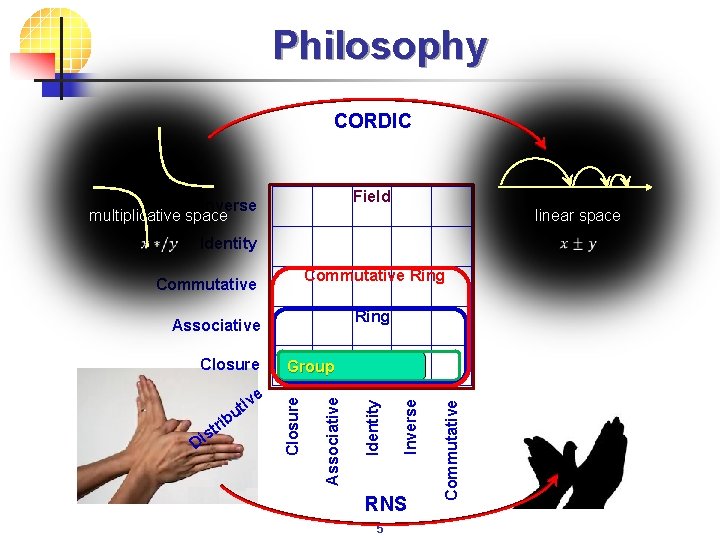
Philosophy CORDIC Field Inverse multiplicative space Identity Commutative Ring Associative RNS 5 Commutative Inverse Di rib t s Identity e iv ut Group Associative Closure linear space

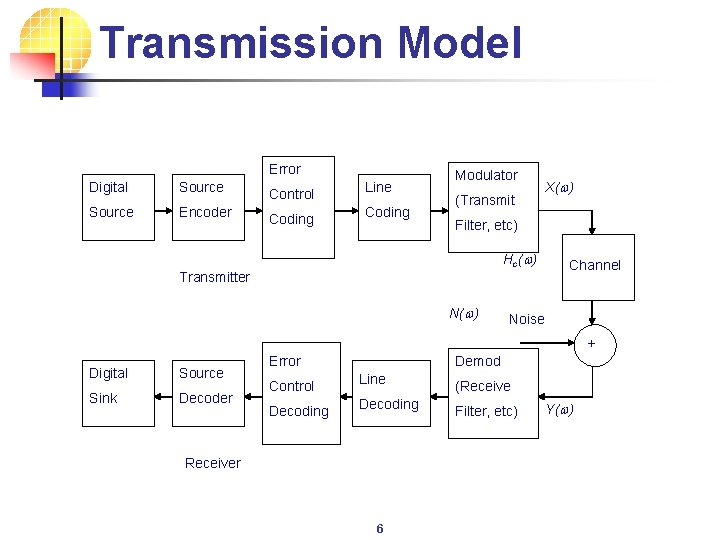
Transmission Model Error Digital Source Encoder Control Coding Line Coding Modulator (Transmit X(w) Filter, etc) H c (w ) Transmitter N(w) Channel Noise + Digital Source Sink Decoder Error Control Decoding Demod Line Decoding Receiver 6 (Receive Filter, etc) Y(w)

Error Models n Binary Symmetric Memoryless Channel Ø Assumes transmitted symbols are binary Ø Errors affect ‘ 0’s and ‘ 1’s with equal probability (i. e. , symmetric) Ø Errors occur randomly and are independent from bit to bit (memoryless) 1 -p 0 0 p IN OUT p 1 1 1 -p 7 p is the probability of bit error or the Bit Error Rate (BER) of the channel

Error Control Techniques n Error detection in a block of data Ø Can then request a retransmission, known as automatic repeat request (ARQ) for sensitive data Ø Appropriate for ü Low delay channels ü Channels with a return path Ø Not appropriate for delay sensitive data, e. g. , real time speech and data n Forward Error Correction (FEC) Ø Coding designed so that errors can be corrected at the receiver Ø Appropriate for delay sensitive and one-way transmission (e. g. , broadcast TV) of data Ø Two main types, namely block codes and convolutional codes. We will only look at block codes 8

(n, k) Block Codes n Data is grouped into blocks of length k bits (dataword) n Each dataword is coded into blocks of length n bits (codeword), where in general n>k n A vector notation is used for the datawords and codewords, Ø Dataword d = (d 1 d 2…. dk) Ø Codeword c = (c 1 c 2……. . cn) n The redundancy introduced by the code is quantified by the code rate, Ø Code rate = k/n Ø i. e. , the higher the redundancy, the lower the code rate 9

Block Code - Example n Dataword length k = 4 n Codeword length n = 7 n This is a (7, 4) block code with code rate = 4/7 n For example, d = (1101), c = (1101001) 10

Error Control Process n Decoder gives corrected data n May also give error flags to Ø Indicate reliability of decoded data Ø Helps with schemes employing multiple layers of error correction 11

Parity Check Codes n Example of a simple block code – Single Parity Check Code Ø In this case, n = k+1, i. e. , the codeword is the dataword with one additional bit Ø For ‘even’ parity the additional bit is, – For ‘odd’ parity the additional bit is 1 -q – That is, the additional bit ensures that there an ‘even’ or ‘odd’ number of ‘ 1’s in the codeword 12

Hamming Distance n Error control capability is determined by the Hamming distance n The Hamming distance between two codewords is equal to the number of differences between them, e. g. , 10011011 11010010 have a Hamming distance = 3 n Alternatively, can compute by adding codewords (mod 2) =01001001 (now count up the ones) 13

Linear Block Codes n For example for a (7, 4) code, only four codewords are required, e. g. , • So, to obtain the codeword for dataword 1011, the first, third and fourth codewords in the list are added together, giving 1011010 • This process will now be described in more detail 14

Linear Block Codes n An (n, k) block code has code vectors d=(d 1 d 2…. dk) and c=(c 1 c 2……. . cn) n The block coding process can be written as c=d. G where G is the Generator Matrix 15

Linear Block Codes n. Sum (mod 2) of any 2 codewords is also a codeword, i. e. , Since for datawords d 1 and d 2 we have; So, 16

Error Correcting Power of LBC n The Hamming distance of a linear block code (LBC) is simply the minimum Hamming weight (number of 1’s or equivalently the distance from the all 0 codeword) of the nonzero codewords n Note d(c 1, c 2) = w(c 1+ c 2) as shown previously n For an LBC, c 1+ c 2=c 3 n So min (d(c 1, c 2)) = min (w(c 1+ c 2)) = min (w(c 3)) n Therefore to find min Hamming distance just need to search among the 2 k codewords to find the min Hamming weight – far simpler 17

Systematic Codes n For a systematic block code the dataword appears unaltered in the codeword – usually at the start n The generator matrix has the structure, k R R = n - k • P is often referred to as parity bits 18

Parity Check Matrix n So H is used to check if a codeword is valid, R = n - k • The rows of H, namely, bi, are chosen to be orthogonal to rows of G, namely ai • Consequently the dot product of any valid codeword with any bi is zero 19

Parity Check Matrix n This is so since, and so, • This means that a codeword is valid (but not necessarily correct) only if c. HT = 0. To ensure this it is required that the rows of H are independent and are orthogonal to the rows of G • That is the bi span the remaining R (= n - k) dimensions of the codespace 20

Parity Check Matrix n Similarly, any received codeword which is in the plane containing a 1 and a 2 (i. e. , a valid codeword) will not have a component in the direction of b 1 yielding a zero dot product between itself and b 1 c 1 a 2 c 2 a 1 c 3 b 1 21

Error Syndrome n For systematic linear block codes, H is constructed as follows, G = [ I | P] and so H = [-PT | I] where I is the k*k identity for G and the R*R identity for H n Example, (7, 4) code, dmin= 3 22

Hamming Codes n Systematic form of (7, 4) Hamming code is, • The original form is non-systematic, • Compared with the systematic code, the column orders of both G and H are swapped so that the columns of H are a binary count 23

Motivation: On-line Repairing 24

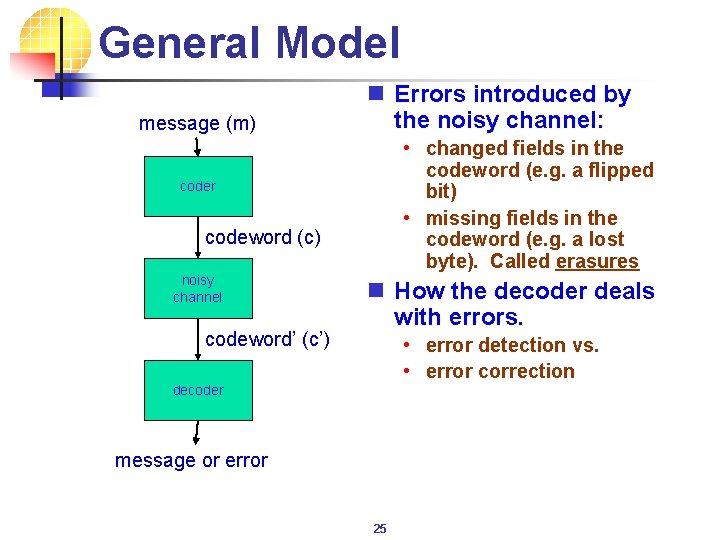
General Model message (m) n Errors introduced by the noisy channel: • changed fields in the codeword (e. g. a flipped bit) • missing fields in the codeword (e. g. a lost byte). Called erasures coder codeword (c) noisy channel codeword’ (c’) n How the decoder deals with errors. • error detection vs. • error correction decoder message or error 25

Channel Coding 26

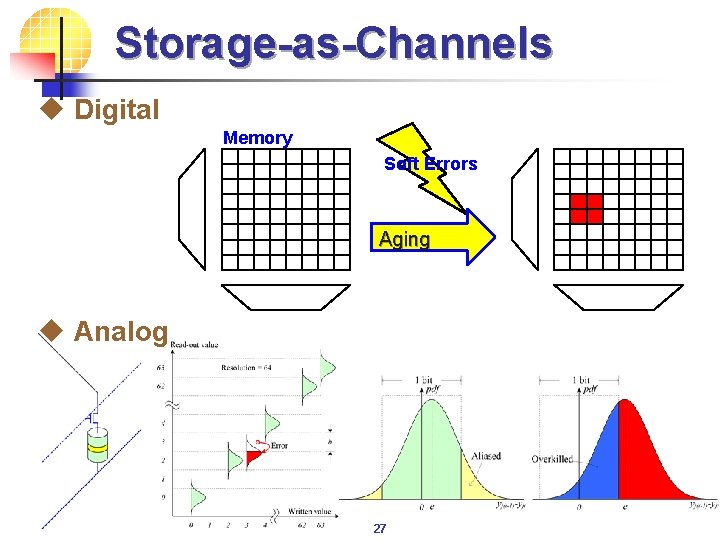
Storage-as-Channels u Digital Memory Soft Errors Aging u Analog 27

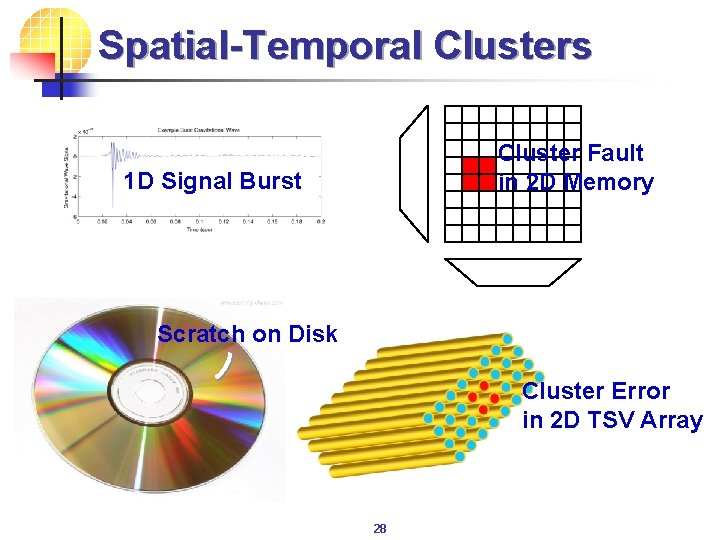
Spatial-Temporal Clusters Cluster Fault in 2 D Memory 1 D Signal Burst Scratch on Disk Cluster Error in 2 D TSV Array 28

Detection and Recognition 1. Digital 1. Hamming Distance 2. Cartesian Distance 2. Analog Error Function Ø x ≠ y how large is x - y ? Ø Vx-y = Vx - Vy if all in f(m, s) 29

Applications • • • Storage: CDs, DVDs, “hard drives”, Wireless: Cell phones, wireless links Satellite and Space: TV, Mars rover, … Digital Television: DVD, MPEG 2 layover High Speed Modems: ADSL, . . n Reed-Solomon codes are by far the most used in practice, including pretty much all the examples mentioned above. n Algorithms for decoding are quite sophisticated. 30

Block Codes message (m) coder codeword (c) noisy channel codeword’ (c’) decoder message or error n Each message and codeword is of fixed size n å = codeword alphabet n k =|m| n = |c| q = |å| n C Sn (codewords) n D(x, y) = number of positions s. t. xi ¹ yi n d = min{D(x, y) : x, y C, x ¹ y} n s = max{D(c, c’)} that the code can correct n Code described as: (n, k, d)q 31

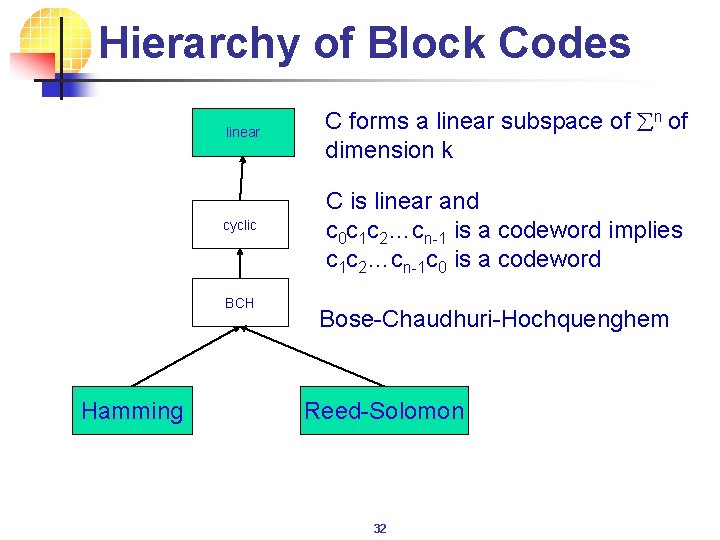
Hierarchy of Block Codes linear cyclic BCH Hamming C forms a linear subspace of n of dimension k C is linear and c 0 c 1 c 2…cn-1 is a codeword implies c 1 c 2…cn-1 c 0 is a codeword Bose-Chaudhuri-Hochquenghem Reed-Solomon 32

Binary Codes n Today we will mostly be considering å = {0, 1} and will sometimes use (n, k, d) as shorthand for (n, k, d)2 n In binary D(x, y) is often called the Hamming distance 33

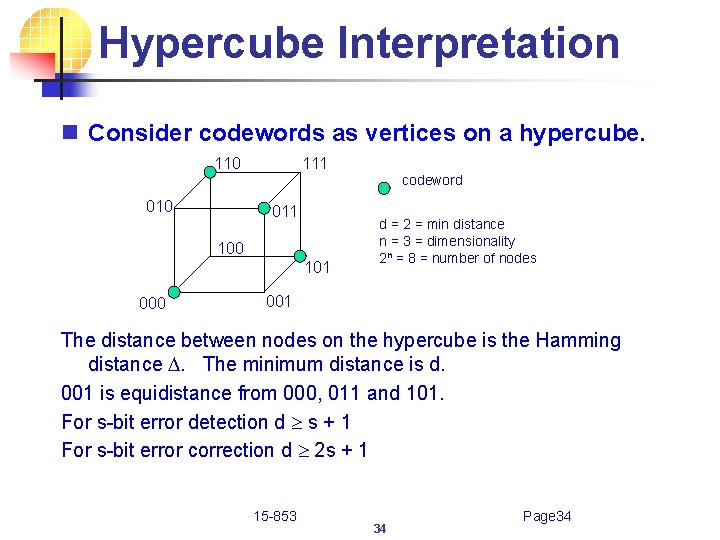
Hypercube Interpretation n Consider codewords as vertices on a hypercube. 110 111 codeword 010 011 100 101 000 d = 2 = min distance n = 3 = dimensionality 2 n = 8 = number of nodes 001 The distance between nodes on the hypercube is the Hamming distance D. The minimum distance is d. 001 is equidistance from 000, 011 and 101. For s-bit error detection d s + 1 For s-bit error correction d 2 s + 1 15 -853 34 Page 34

Error Detection with Parity Bit n n A (k+1, k, 2)2 systematic code Encoding: m 1 m 2…mkpk+1 where pk+1 = m 1 m 2 … mk n d = 2 since the parity is always even (it takes two bit changes to go from one codeword to another). n Detects one-bit error since this gives odd parity n Cannot be used to correct 1 -bit error since any odd -parity word is equal distance D to k+1 valid codewords. 35

Error Correcting One Bit Messages n How many bits do we need to correct a one bit error on a one bit message? 110 111 10 010 11 011 100 101 000 001 3 bits 0 -> 000, 1 -> 111 (n=3, k=1, d=3) 2 bits 0 -> 00, 1 -> 11 (n=2, k=1, d=2) In general need d 3 to correct one error. Why ? & Why not ? 36

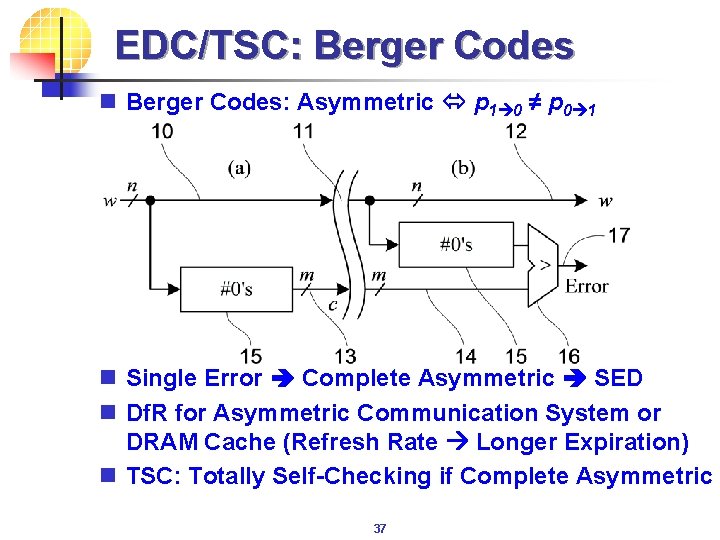
EDC/TSC: Berger Codes n Berger Codes: Asymmetric p 1 0 ≠ p 0 1 n Single Error Complete Asymmetric SED n Df. R for Asymmetric Communication System or DRAM Cache (Refresh Rate Longer Expiration) n TSC: Totally Self-Checking if Complete Asymmetric 37

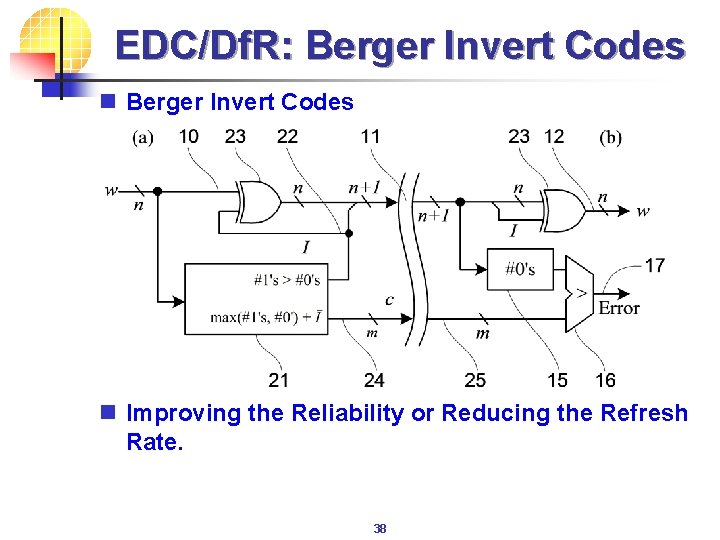
EDC/Df. R: Berger Invert Codes n Improving the Reliability or Reducing the Refresh Rate. 38

Other Linear (line-like) Detector 1. 2. 3. 4. Sum: SED Residue: SED Product: SED Laser/Optical Sensor Cartesian-Space Error Location 39

Example of (6, 3, 3)2 systematic code message codeword 000000 001011 010101 011 100 101 110 111 n Definition: A Systematic code is one in which the message appears in the codeword 011110 100110 101101 110011 111000 40

Error Correcting Multibit Messages n We will first discuss Hamming Codes n Detect and correct 1 -bit errors. n Codes are of form: (2 r-1, 2 r-1 – r, 3) for any r > 1 n e. g. (3, 1, 3), (7, 4, 3), (15, 11, 3), (31, 26, 3), … n which correspond to 2, 3, 4, 5, … “parity bits” (i. e. n-k) n The high-level idea is to “localize” the error. n Any specific ideas? 41

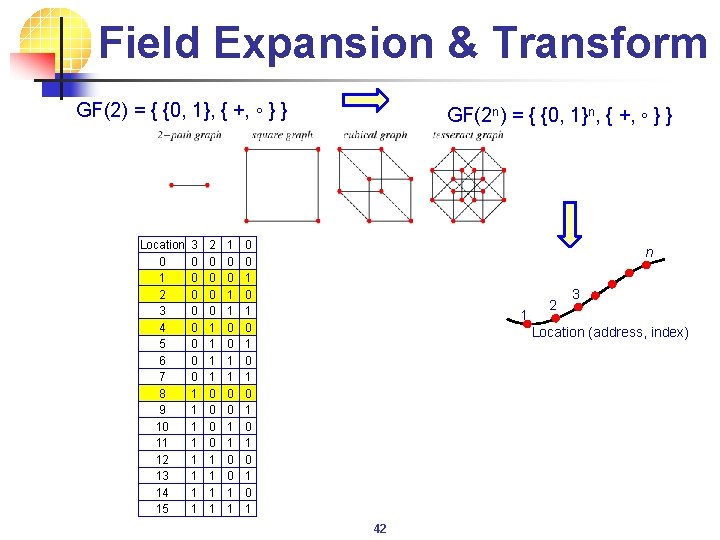
Field Expansion & Transform GF(2) = { {0, 1}, { +, ◦ } } Location 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 0 0 0 0 1 1 1 1 2 0 0 0 0 1 1 1 1 1 0 0 1 1 GF(2 n) = { {0, 1}n, { +, ◦ } } 0 0 1 0 1 n 1 2 3 Location (address, index) 42

Hamming Codes n Can be generalized to any power of 2 Ø n = 2 r – 1 (15 in the example) Ø (n-k) = r (4 in the example) Ø d = 3 (discuss later) Ø Can correct one error, but can’t tell difference between one and two! Ø Gives (2 r-1, 2 r-1 -r, 3) code n Extended Hamming code Ø Add back the parity bit at the end Ø Gives (2 r, 2 r-1 -r, 4) code Ø Can correct one error and detect 2 Ø (not so obvious) 43

Lower bound on parity bits n How many nodes in hypercube do we need so that d = 3? n Each of the 2 k codewords eliminates n neighbors plus itself, i. e. n+1 In previous hamming code 15 11 + log 2(15+1) = 15 Hamming Codes are called perfect codes since they match the lower bound exactly 44

Linear Block Codes n Linearity n Example : 4/7 Hamming Code Ø k = 4, n = 7 Ø 4 message bits at (3, 5, 6, 7) Ø 3 parity bits at (1, 2, 4) Ø Error correcting capability =1 Ø Error detecting capability = 2 Ø What is G? 45

Linear Codes n If å is a field, then ån is a vector space n Definition: C is a linear code if it is a linear subspace of ån of dimension k. n This means that there is a set of k basis vectors vi ån (1 i k) that span the subspace. n i. e. every codeword can be written as: c = a 1 v 1 + … + ak vk ai å 46

Linear Block Codes n #parity bits n-k (=1 for Parity Check) n Message m = {m 1 m 2 … mk} n Transmitted Codeword c = {c 1 c 2 … cn} n A generator matrix Gkxn n What is G for repetition code? n For parity check code? 47

Linear Codes n Basis vectors for the (7, 4, 3)2 Hamming code: m 7 m 6 m 5 p 4 m 3 p 2 p 1 v 1 = 1 0 0 1 1 v 2 = 0 1 0 1 0 v 3 = 0 0 1 1 0 0 1 v 4 = 0 0 1 1 1 How can we see that d = 3? 48

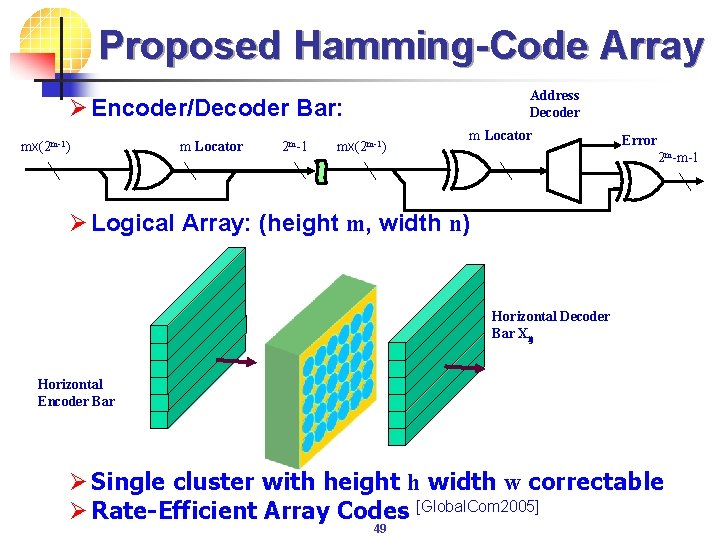
Proposed Hamming-Code Array Address Decoder Ø Encoder/Decoder Bar: mx(2 m-1) m Locator 2 m-1 mx(2 m-1) m Locator Error 2 m-m-1 Ø Logical Array: (height m, width n) Horizontal Decoder Bar Xij Horizontal Encoder Bar Ø Single cluster with height h width w correctable Ø Rate-Efficient Array Codes [Global. Com 2005] 49

Generator and Parity Check Matrices n n n n Generator Matrix: A k x n matrix G such that: C = {x. G | x åk} Made from stacking the basis vectors Parity Check Matrix: An (n – k) x n matrix H such that: C = {y ån | Hy. T = 0} Codewords are the null space of H These always exist for linear codes 50

Advantages of Linear Codes • Encoding is efficient (vector-matrix multiply) • Error detection is efficient (vector-matrix multiply) • Syndrome (Hy. T) has error information • Gives qn-k sized table for decoding Useful if n-k is small 51

Example and “Standard Form” n For the Hamming (7, 4, 3) code: By swapping columns 4 and 5 it is in the form Ik, A. A code with a matrix in this form is systematic, and G is in “standard form” 52

Relationship of G and H n If G is in standard form [Ik, A] then H = [AT, In-k] n Example of (7, 4, 3) Hamming code: transpose 53

Proof that H is a Parity Check Matrix Suppose that x is a message. Then H(x. G)T = H(GTx. T) = (HGT)x. T = (ATIk+In-k. AT)x. T = (A T + AT)x. T = 0 Now suppose that Hy. T = 0. Then ATi, * y. T[1. . k] + y. Tk+i = 0 (where ATi, * is row i of AT and y. T[1. . k] are the first k elements of y. T]) for 1 i n-k. Thus, y[1. . k] A*, i = yk+i where A*, i is now column i of A, and y[1. . k] are the first k elements of y, so y[k+1…n] = y[1. . k]A. Consider x = y[1. . k]. Then x. G = [y [1. . k] | y[1. . k]A] = y. Hence if Hy. T = 0, y is the codeword for x = y[1. . k]. 54

The d of linear codes n Theorem: Linear codes have distance d if every set of (d-1) columns of H are linearly independent (i. , e. , sum to 0), but there is a set of d columns that are linearly dependent. n Proof: if d-1 or fewer columns are linearly dependent, then for any codeword y, there is another codeword y’, in which the bits in the positions corresponding to the columns are inverted, that both have the same syndrome (0). n If every set of d-1 columns is linearly independent, then changing any d-1 bits in a codeword y must also change the syndrome (since the d-1 corresponding columns cannot sum to 0). 55

Channel Capacity n C(p) is called the channel capacity n For binary symmetric channel, n Can we really design codes that achieve this rate? How? 56

Parity Check Codes n #information bits transmitted = k n #bits actually transmitted = n = k+1 n Code Rate R = k/n = k/(k+1) n Error detecting capability = 1 n Error correcting capability = 0 57

2 -D Parity Check n Rate? n Error detecting capability? n Error correcting capability? 1 0 0 0 1 1 0 0 1 1 0 Last column consists of check bits for each row 1 0 0 1 1 1 Bottom row consists of check bit for each column 58

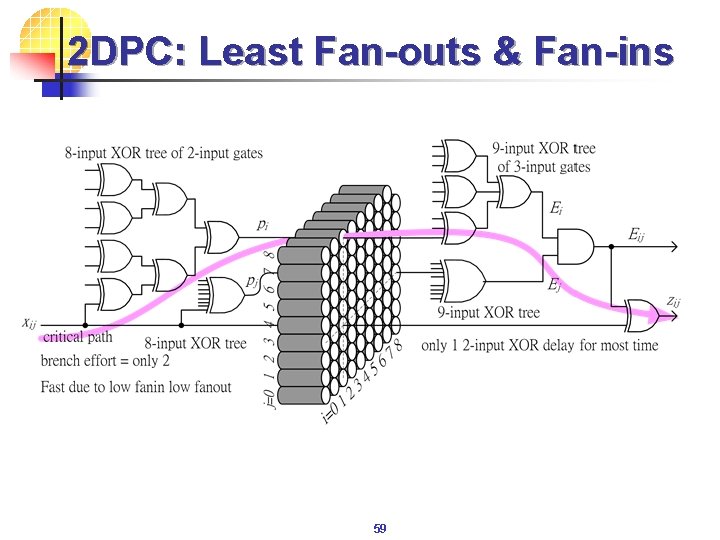
2 DPC: Least Fan-outs & Fan-ins 59

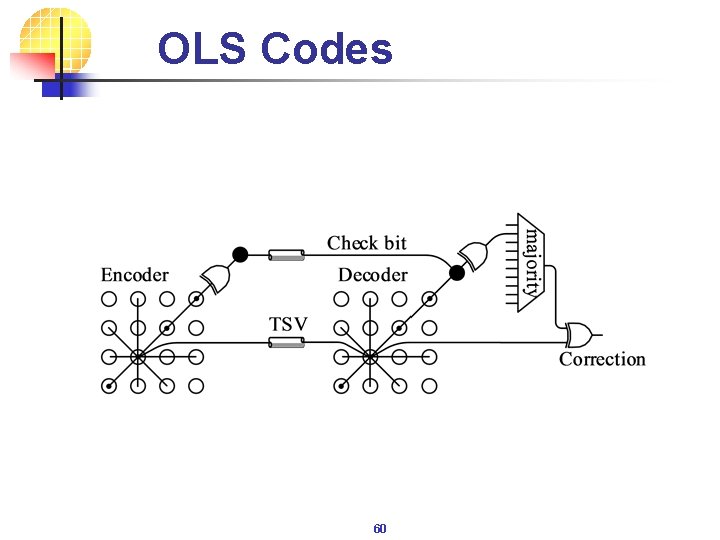
OLS Codes 60

Cyclic codes n Special case of Linear Block Codes n Cyclic shift of a codeword is also a codeword Ø Easy to encode and decode, Ø Can correct continuous bursts of errors Ø CRC (used in Wireless LANs), BCH codes, Hamming Codes, Reed Solomon Codes (used in CDs) 61

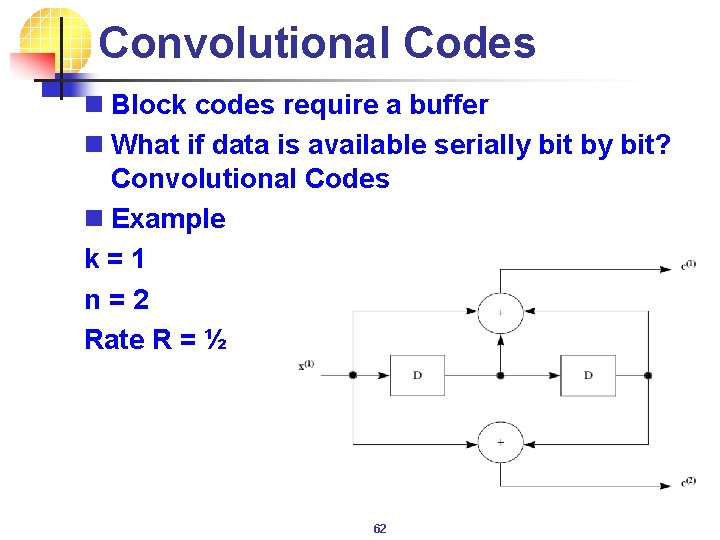
Convolutional Codes n Block codes require a buffer n What if data is available serially bit by bit? Convolutional Codes n Example k = 1 n = 2 Rate R = ½ 62

Convolutional Codes n Encoder consists of shift registers forming a finite state machine n Decoding is also simple – Viterbi Decoder which works by tracking these states n First used by NASA in the voyager space programme n Extensively used in coding speech data in mobile phones 63

Achieving Capacity n Do Block codes and Convolutional codes achieve Shannon Capacity? Actually they are far away n Achieving Capacity requires large k (block lengths) n Decoder complexity for both codes increases exponentially with k – not feasible to implement 64

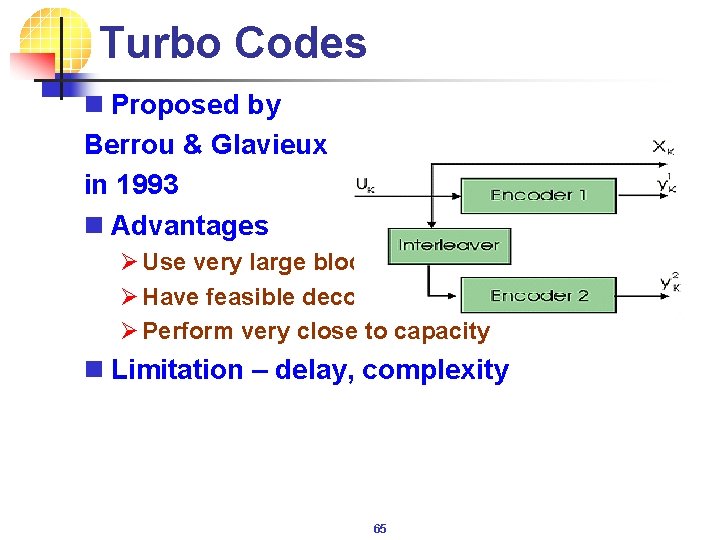
Turbo Codes n Proposed by Berrou & Glavieux in 1993 n Advantages Ø Use very large block lengths Ø Have feasible decoding complexity Ø Perform very close to capacity n Limitation – delay, complexity 65

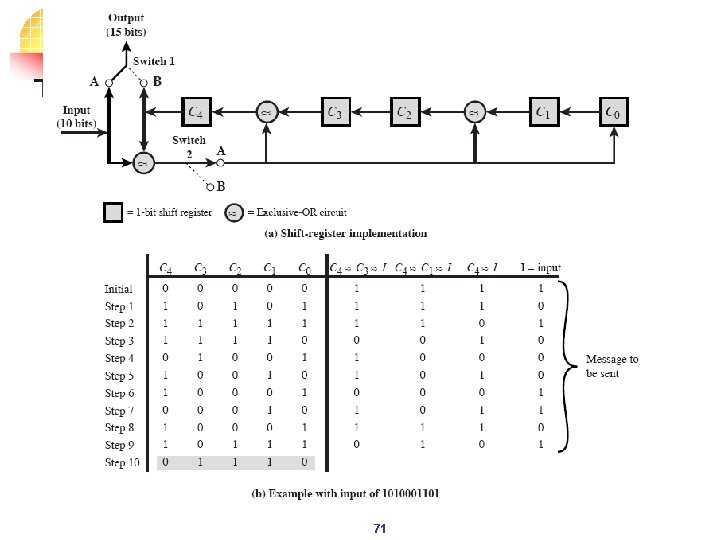
Cyclic Redundancy Check (CRC) n Transmitter ØFor a k-bit block, transmitter generates an (n-k)-bit frame check sequence (FCS) ØResulting frame of n bits is exactly divisible by predetermined number n Receiver ØDivides incoming frame by predetermined number ØIf no remainder, assumes no error 66

CRC using Modulo 2 Arithmetic n Exclusive-OR (XOR) operation n Parameters: Ø T = n-bit frame to be transmitted Ø D = k-bit block of data; the first k bits of T Ø F = (n – k)-bit FCS; the last (n – k) bits of T Ø P = pattern of n–k+1 bits; this is the predetermined divisor Ø Q = Quotient Ø R = Remainder n For T/P to have no remainder, start with n Divide 2 n-k. D by P gives quotient and remainder n Use remainder as FCS 67

CRC using Modulo 2 Arithmetic n Does R cause T/P have no remainder? n Substituting, Ø No remainder, so T is exactly divisible by P 68

CRC using Polynomials n All values expressed as polynomials Ø Dummy variable X with binary coefficients n Widely used versions of P(X) Ø CRC– 12 ü X 12 + X 11 + X 3 + X 2 + X + 1 Ø CRC– 16 ü X 16 + X 15 + X 2 + 1 Ø CRC – CCITT ü X 16 + X 12 + X 5 + 1 Ø CRC – 32 ü X 32 + X 26 + X 23 + X 22 + X 16 + X 12 + X 11 + X 10 + X 8 + X 7 + X 5 + X 4 + X 2 + X + 1 69

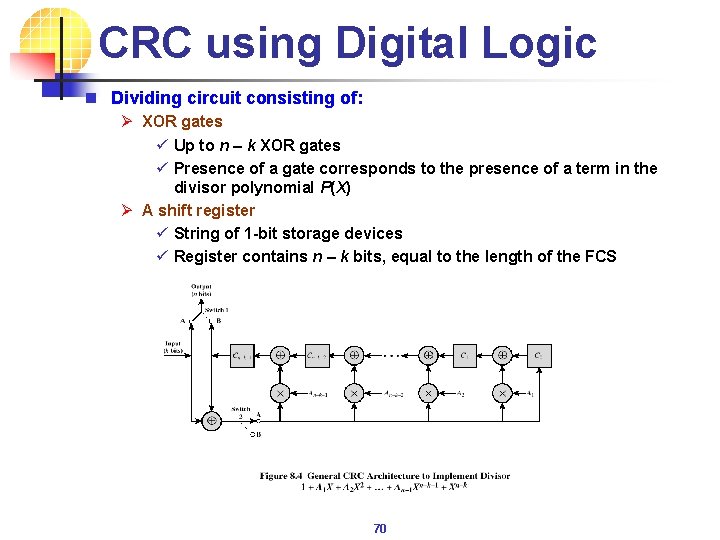
CRC using Digital Logic n Dividing circuit consisting of: Ø XOR gates ü Up to n – k XOR gates ü Presence of a gate corresponds to the presence of a term in the divisor polynomial P(X) Ø A shift register ü String of 1 -bit storage devices ü Register contains n – k bits, equal to the length of the FCS 70

71

BCH Codes n FG(2): Ø FG(2)n: Ø Hypercube: n independent dimensions of FG(2) Ø Address of Location Locating Error Ø BCH’s View: codeword as coefficients of eq. Ø Error locations will be the roots n-k roots Ø Root-solving laws Field Ø FG(2)n FG(2 n) Ø Bitwise Addition Ø Special Multiplication: Primitive-polynomial Residue (Galois Multiplicaion) 72

Hamming-Code Error Location n Parity Check Matrix H: 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 n Possible Error Location: 0 1 2 3 4 5 6 7 8 9 10111213141516171819202122232425262728293031 n If there are 2 errors at x and y: f(x) + g(y) = s 2 x + y = s 1 73

BCH Codes n Field Expansion GF(2 n) Location Find Roots n For positive pair of integers m and t, a (n, k) BCH n code has parameters: Ø Block length: n = 2 m – 1 1 2 3 Location (address, index) Ø Number of check bits: n – k £ mt Ø Minimum distance: dmin ³ 2 t + 1 n Correct combinations of t or fewer errors n Flexibility in choice of parameters Ø Block length, code rate 74

Galois Multiplication n 75

Example of GF(24) n Operations of Hexi-decimal Field 76

Reed-Solomon Codes n Subclass of nonbinary BCH codes n Data processed in chunks of m bits, called symbols n An (n, k) RS code has parameters: Ø Symbol length: m bits per symbol Ø Block length: n = 2 m – 1 symbols = m(2 m – 1) bits Ø Data length: k symbols Ø Size of check code: n – k = 2 t symbols = m(2 t) bits Ø Minimum distance: dmin = 2 t + 1 symbols 77