Discrete Mathematics Mathematical Logic Mathematical Logic Definition Methods

































































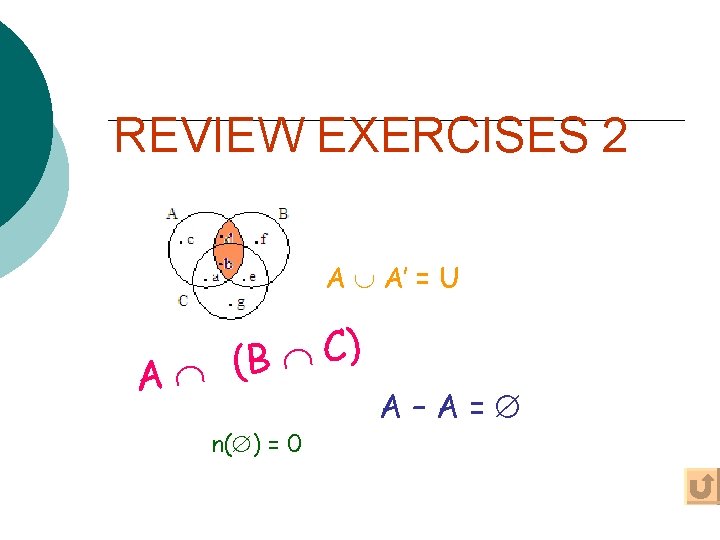
- Slides: 78

Discrete Mathematics Mathematical Logic

Mathematical Logic Definition: Methods of reasoning, provides rules and techniques to determine whether an argument is valid Theorem: a statement that can be shown to be true (under certain conditions) Example: If x is an even integer, then x + 1 is an odd integer This statement is true under the condition that x is an integer is true 2

Mathematical Logic A statement, or a proposition, is a declarative sentence that is either true or false, but not both Uppercase letters denote propositions Examples: P: 2 is an even number (true) Q: 7 is an even number (false) R: A is a vowel (true) The following are not propositions: P: My cat is beautiful Q: My house is big 3

Propositions • • A statement that has a truth value Which of the following are propositions? – – – The Washington State flag is red It snowed in Whistler, BC on January 4, 2008. Hillary Clinton won the democratic caucus in Iowa Space aliens landed in Roswell, New Mexico Ron Paul would be a great president Turn your homework in on Wednesday Why are we taking this class? If n is an integer greater than two, then the equation an + bn = cn has no solutions in non-zero integers a, b, and c. Every even integer greater than two can be written as the sum of two primes This statement is false Propositional variables: p, q, r, s, . . . Truth values: T for true, F for false

Mathematical Logic Truth value One of the values “truth” (T) or “falsity” (F) assigned to a statement Negation The negation of P, written P, is the statement obtained by negating statement P Example: P: A is a consonant P: it is the case that A is not a consonant Truth Table P P T F F T 5

Mathematical Logic Conjunction Let P and Q be statements. The conjunction of P and Q, written P ^ Q , is the statement formed by joining statements P and Q using the word “and” The statement P ^ Q is true if both p and q are true; otherwise P ^ Q is false Truth Table for Conjunction: P Q P ˄Q F F T T T 6

Mathematical Logic Disjunction Let P and Q be statements. The disjunction of P and Q, written P v Q , is the statement formed by joining statements P and Q using the word “or” The statement P v Q is true if at least one of the statements P and Q is true; otherwise P v Q is false The symbol v is read “or” Truth Table for Disjunction: P Q P ˅Q F F T T T F T T 7

Mathematical Logic Implication Let P and Q be statements. The statement “if P then Q” is called an implication or condition. The implication “if P then Q” is written P Q P is called the hypothesis, Q is called the conclusion Truth Table for Implication: P Q F F T F T T T T 8

Mathematical Logic Implication Let P: Today is Sunday and Q: I will wash the car. P Q: If today is Sunday, then I will wash the car The converse of this implication is written Q P If I wash the car, then today is Sunday The inverse of this implication is P Q If today is not Sunday, then I will not wash the car The contrapositive of this implication is Q P If I do not wash the car, then today is not Sunday 9

Mathematical Logic Biimplication Let P and Q be statements. The statement “P if and only if Q” is called the biimplication or biconditional of P and Q The biconditional “P if and only if Q” is written P Q “P if and only if Q” Truth Table for the Biconditional: P Q F F T F T F F T T T 10

Mathematical Logic Precedence of logical connectives is: highest ^ second highest v third highest → fourth highest ↔ fifth highest 11

English and Logic You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old q: you can ride the roller coaster r: you are under 4 feet tall s: you are older than 16 ( r s) q s (r q)

Mathematical Logic A compound proposition is a Tautology if it is always true Contradiction if it is always false Contingency if it can be either true or false 13

Mathematical Logically Implies A statement formula A is said to logically imply a statement formula B if the statement formula A → B is a tautology. If A logically implies B, then symbolically we write A → B Logically Equivalent A statement formula A is said to be logically equivalent to a statement formula B if the statement formula A ↔ B is a tautology. If A is logically equivalent to B , then symbolically we write A B 14

15

16

Quantifiers and First Order Logic Predicate or Propositional Function Let x be a variable and D be a set; P(x) is a sentence Then P(x) is called a predicate or propositional function with respect to the set D if for each value of x in D, P(x) is a statement; i. e. , P(x) is true or false Moreover, D is called the domain (universe) of discourse and x is called the free variable 17

Quantifiers and First Order Logic Universal Quantifier Let P(x) be a predicate and let D be the domain of the discourse. The universal quantification of P(x) is the statement: For all x, P(x) or For every x, P(x) The symbol is read as “for all and every” x, or x D, P(x) Two-place predicate: x, y, P(x, y) 18

Quantifiers and First Order Logic Existential Quantifier Let P(x) be a predicate and let D be the universe of discourse. The existential quantification of P(x) is the statement: There exists x, P(x) The symbol is read as “there exists” x D, P(x) Bound Variable or x, P(x) The variable appearing in: x, P(x) or x, P(x) 19

Quantifiers and First Order Logic Negation of Predicates (De. Morgan’s Laws) x, P(x) x, P(x) Example: If P(x) is the statement “x has won a race” where the domain of discourse is all runners, then the universal quantification of P(x) is x, P(x) , i. e. , every runner has won a race. The negation of this statement is “it is not the case that every runner has won a race. Therefore there exists at least one runner who has not won a race. Therefore: x, P(x) 20


BASIC CONCEPTS OF SETS Define a set Represent a set Define the number of elements of a set Practice Problems 1 Compare sets Recognize different types of set Practice Problems 2 Define the subsets of a set OPERARe. Tv. Iie. Ow. NESxe. Orc. Nise. Ss. E 1 TS Determine the union of two or more sets Practice Problems 3 Determine the intersection of two or more sets Practice Problems 4 Determine the complement of a set Determine the difference of two sets Practice Problems 5 Review Exercises 2 Lesson is over

Defining a Set Definition A collection of well-defined objects is called a set. For example, ‘the set of former Nobel Prize winners’ is a well-defined set ‘the set of tall students in our university’ is not a well-defined set It’s interesting Note

Note Sets must be well-defined. A set is well-defined if we can tell whether a particular object is an element of that set.

Defining a Set Definition Each object in a set is called an element or a member of the set. Sets notation: Elements Notation: For example, A, B, C, … a, b, c, … Note A = {a, b, c, d} b A ‘b is an element of set A’ or ‘b is in A’ f A ‘f is not an element of set A’ or ‘f is not in A’ Example 1 Check

Note Each element of the set is written only once. The order of elements in a set is not important.

George Cantor (1845 -1918) George Cantor was born March 3, 1845 in St. Petersburg, Russia and died January 6, 1918 in Halle, Germany. Cantor was the first mathematician who defined the basic ideas of set theory. Using ingenious methods, he proved remarkable things about infinite sets.

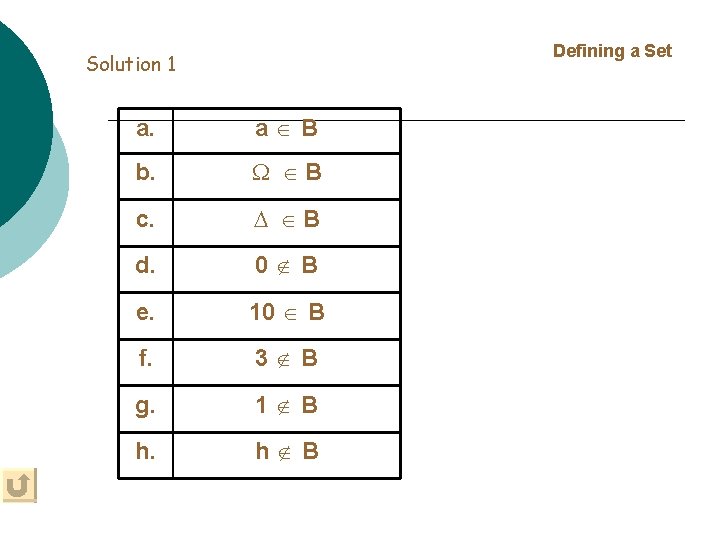
Defining a Set Solution 1 a. a B b. B c. B d. 0 B e. 10 B f. 3 B g. 1 B h. h B

Representing Sets 1. The List Method 1. The Defining-Property Method 1. The Venn Diagram Method It’s interesting

Representing Sets The List Method For instance, C = {I, You, He, She, We, They} A = { , , , } Example 2 Check

Solution 2 • A = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday} 1. B = {a, b, c, d, e} • C = {m, a, t, h, e, i, c, s} Each element is written only once. • D = {1, 2, 3, …, 1000} The first few elements of D are written to establish a pattern. The three dots (…), called an ellipsis, indicate that the last continues in the same way up to the last number of the set, which is 1000. • Representing Sets W = {0, 1, 2, 3, …} If we don’t put a number after the ellipsis, this means that the list doesn’t end.

Representing Sets The Defining-Property Method For example, B={x| x is a season of the year} B is of all x x is a season of the year such that the set When we use the defining-property method Note we can use the symbol ‘: ’ instead of ‘|’. Example 3 Check

Solution 3 1. A = {the days of the weekend}, or A = {x| x is a day of the weekend} 1. B = {x| x is a season of the year} 1. C = {y| y is a whole number less than 25 & divisible by 3} • D = {z| z is a blood type} Representing Sets

Representing Sets The Venn Diagram Method As an example, A. a . b. c Note Each element of the set is represented by a point inside the closed shape. Example 4 Check

John Venn (1834 -1923) John Venn was born Cambridge, England. Venn diagrams (a Augustway 4, of 1834 in Hull, diagrammatic Yorkshire, and representing sets & their. England relationships) were died April 1923 in in 1880 by John Venn. 4, introduced

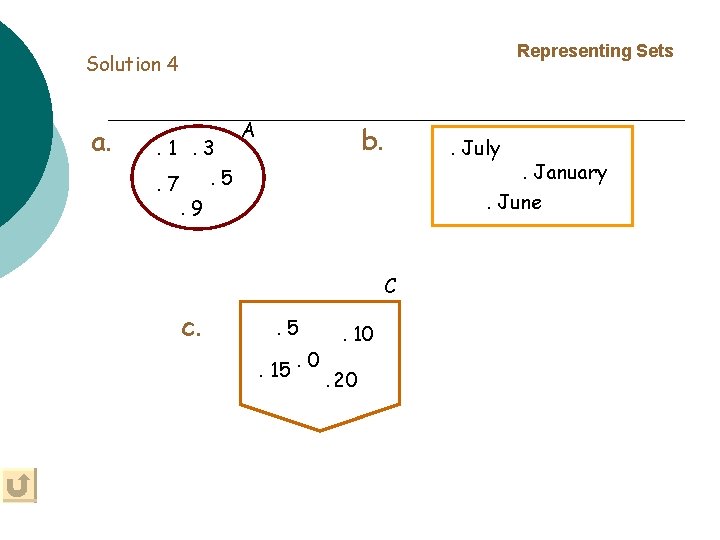
Representing Sets Solution 4 a. . 1. 3. 5. 7. 9 A b. . July . January. June C c. . 5 . 10 . 15. 0. 20

Definition Number of Elements of a Set The number of elements in a set A is called the cardinal number of the set A. Denotation: n(A) Example 5 Check

Solution 5 Number of Elements of a Set a. n(A) = 9 a. {a, b} & {e, f} are elements of set B, therefore n(B) = 5 a. E = {M, A, T, H, E, I, C, S} so n(E) = 8 a. Nobody lives on the sun, so n(P) = 0

Practice Problems 1 B={x| x is a season of the year} f A A = { , , , } A. a. b n(A) . c

Comparing Sets 1. Equivalent Sets 1. Equal Sets Note

Comparing Sets Equivalent Sets Definition Two sets are equivalent if they have the same number of elements. If A & B are equivalent A B ‘set A is equivalent to set B’ For example, A = {a, b, c, d} & B = {1, 2, 3, 4} n(A) = n(B) = 4 so A B

Comparing Sets Equal Sets Definition Two sets are equal if they have exactly the same elements. If A & B are equal A=B ‘set A is equal to set B’ Example 6 Check

Solution 6 Comparing Sets A & B contain exactly the same elements, therefore they are equal. Therefore, we can write A = B.

Note If A is equal to B, then A is also equivalent to B. A=B A B However, If A is equivalent to B, then A might not be equal to B. A B A= B

Types of Set • Empty (Null) Set • The Universal Set • Finite & Infinite Sets

Types of Set Empty (Null) Set Definition The set that contains no element is called the empty set or the null set. Denotation: or { } As an example, A = {x| x is a month containing 32 days} So A = & n( ) = 0

Types of Set The Universal Set Definition The Universal set is the set of all elements under consideration in a given discussion. Denotation: For instance, U U = {a, b, c, d, e, f, g, h, I, j} A = {a, b, c} B = {c, d, e} C = {f, g, h}

Types of Set Finite & Infinite Sets Definition If the number of elements in a set is a whole number, the set is a finite set. If a set is not finite then it is an infinite set. As an example, ‘the set of days of the week’ is a finite set ‘the set of whole numbers’ is an infinite set Example 7 Check

Solution 7 Types of Set 1. A is a finite set 1. B is a finite set 1. E is a finite set 1. The set of whole numbers is an infinite set 1. The set of integers is an infinite set • F = & n( ) = 0, so F is a finite set

Practice Problems 2 A=B A B n( ) = 0 U = {a, b, c, d, e, f, g, h, I, j} A=B Z = {… -3, -2, -1, 0, 1, 2, 3, …}

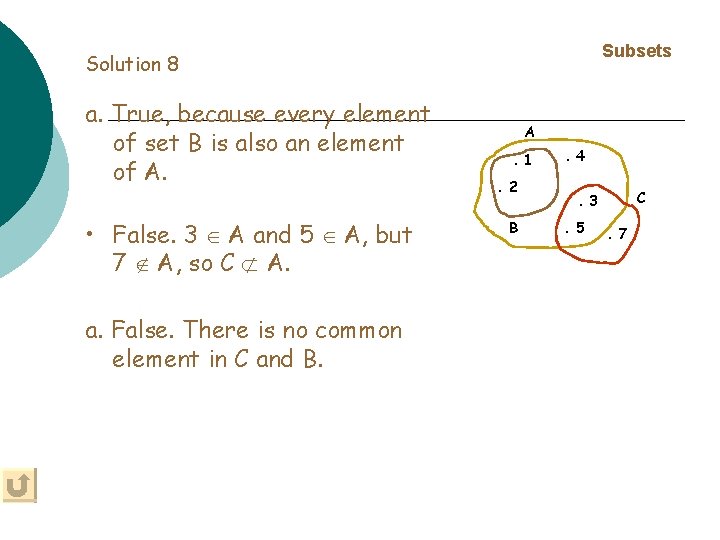
Subsets Definition Set A is a subset of set B if every element of A is also an element of B. • If A B ‘A is a subset of B’, or ‘A is contained in B’ • If B A ‘B is a super set of A’, or ‘B contains A’ B. 2. 7 Example 8 A. 1. 3. 5 U. 6. 4 . 8 A B B U A U Check

Subsets Solution 8 a. True, because every element of set B is also an element of A. • False. 3 A and 5 A, but 7 A, so C A. a. False. There is no common element in C and B. A. 1. 2 B . 4 C . 3. 5 . 7

Properties Subsets • Every set is a subset of itself. (A A) • The empty set is a subset of any set. ( A) • If A B and B A then A = B. • If A B, B C then A C. (Transitive) • The number of subsets of a set with n elements is 2 n.

REVIEW EXERCISES 1 A=B A B , { S= f A } , , D. a. b n( ) = 0 . c

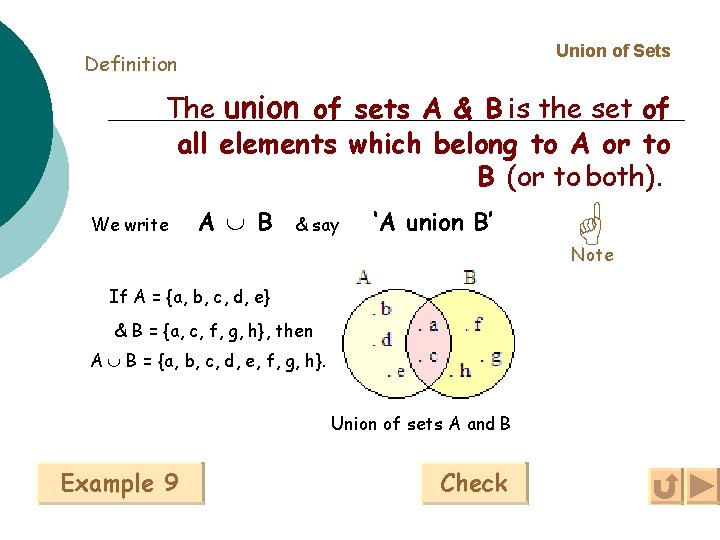
Union of Sets Definition The union of sets A & B is the set of all elements which belong to A or to B (or to both). We write A B & say ‘A union B’ Note If A = {a, b, c, d, e} & B = {a, c, f, g, h}, then A B = {a, b, c, d, e, f, g, h}. Union of sets A and B Example 9 Check

Note If a A B then a A or a B. Each element must be written only once in the union of sets.

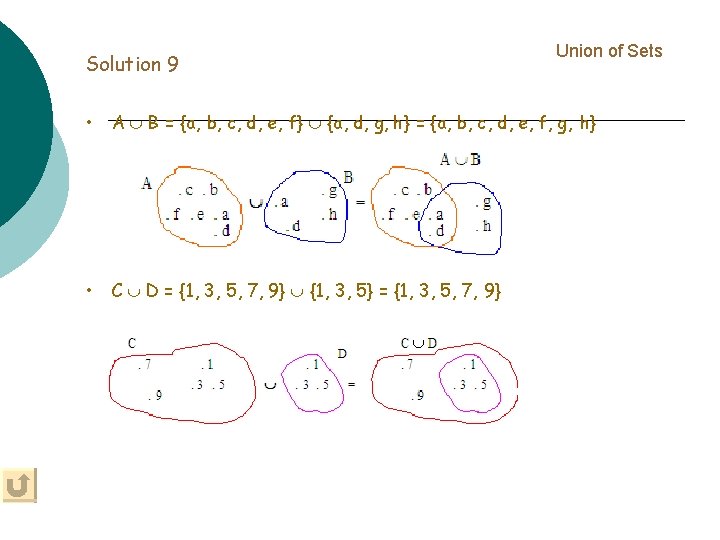
Solution 9 Union of Sets • A B = {a, b, c, d, e, f} {a, d, g, h} = {a, b, c, d, e, f, g, h} • C D = {1, 3, 5, 7, 9} {1, 3, 5} = {1, 3, 5, 7, 9}

Union of Sets Properties of the Union Let A, B, C be three sets, then the following statements are true: • A A= A (idempotent law) • A B=B A (commutative property) • A (B C) = (A B) C (associative property) • A = A (identity law) • A U= U Example 10 Check

Solution 10 Union of Sets • A A = {a, b, c, d} So, A A = A. • A = {a, b, c, d} { } = {a, b, c, d} So, A = A. • A B = {a, b, c, d} {c, d, e, f} = {a, b, c, d, e, f} B A = {c, d, e, f} {a, b, c, d} = {a, b, c, d, e, f} So, A B = B A. • B C = {c, d, e, f} {a, d, e, g} = {a, c, d, e, f, g} A (B C) = {a, b, c, d} {a, c, d, e, f, g} = {a, b, c, d, e, f, g} A B = {a, b, c, d} {c, d, e, f} = {a, b, c, d, e, f} (A B) C = {a, b, c, d, e, f} {a, d, e, g} = {a, b, c, d, e, f, g}. We can easily see that A (B C) = (A B) C = {a, b, c, d, e, f, g}.

Practice Problems 3 A B = B A n( ) = 0 U = {a, b, c, d, e, f, g, h, I, j} A B Z = {… -3, -2, -1, 0, 1, 2, 3, …}

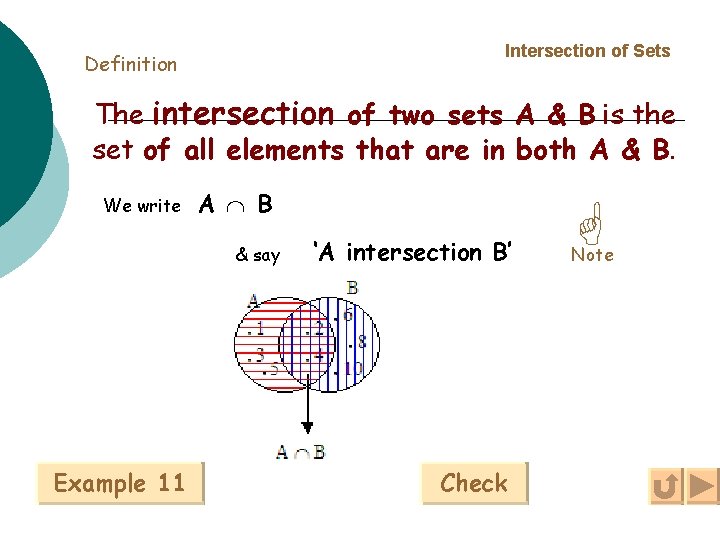
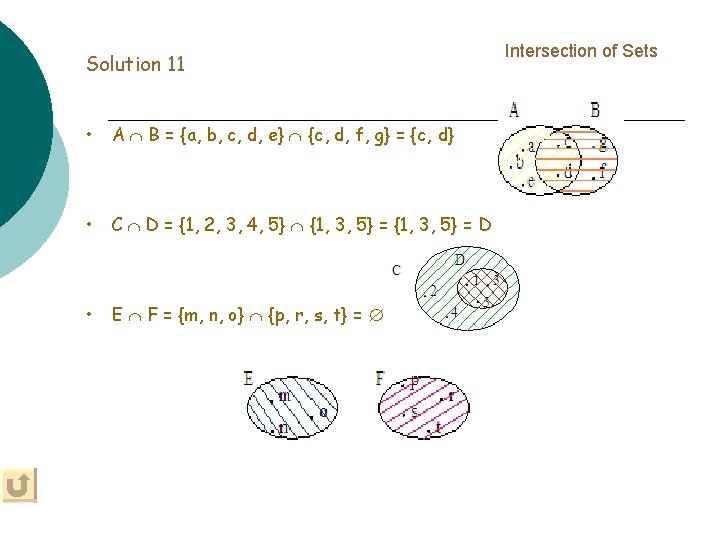
Intersection of Sets Definition The intersection of two sets A & B is the set of all elements that are in both A & B. We write A B & say Example 11 ‘A intersection B’ Check Note

Note If a A B then a A & a B.

Solution 11 • A B = {a, b, c, d, e} {c, d, f, g} = {c, d} • C D = {1, 2, 3, 4, 5} {1, 3, 5} = D • E F = {m, n, o} {p, r, s, t} = Intersection of Sets

Intersection of Sets Properties of the Intersection Let A, B, & C be three sets, then the following statements are true: • A A= A (idempotent law) • A B=B A (commutative property) • A (B C) = (A B) C (associative property) • A = (identity law) • A U= A Example 12 Check

Solution 12 Intersection of Sets • A A = {1, 2, 3, 4} = A • A = {1, 2, 3, 4} { } = • A B = {1, 2, 3, 4} {2, 3, 5, 6} = {2, 3} B A = {2, 3, 5, 6} {1, 2, 3, 4} = {2, 3} So, A B = B A • (A B) C = {2, 3} {3, 4, 5, 7} = {3} A (B C) = {1, 2, 3, 4} {2, 3} = {3} So, (A B) C = A (B C)

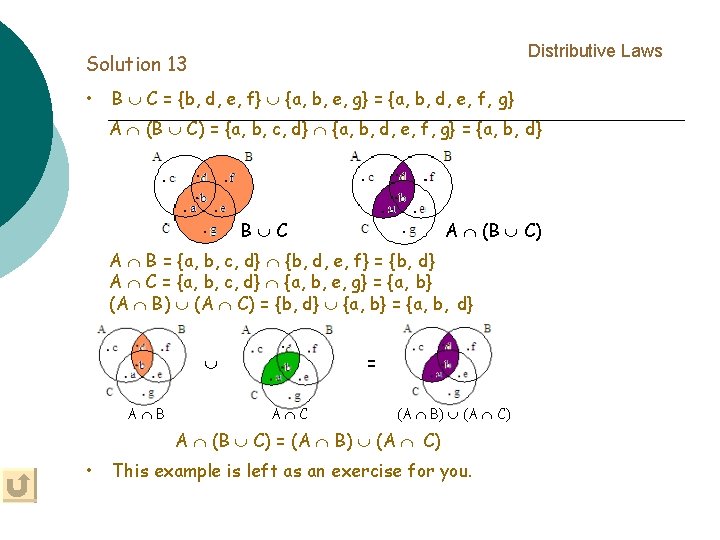
Intersection of Sets Rule Distributive Laws For any three sets A, B, & C, the following statements are true: is distributive over from the left & the right. A (B C) = (A B) (A C) (A B) C = (A C) (B C) Example 13 Check

Distributive Laws Solution 13 • B C = {b, d, e, f} {a, b, e, g} = {a, b, d, e, f, g} A (B C) = {a, b, c, d} {a, b, d, e, f, g} = {a, b, d} B C A (B C) A B = {a, b, c, d} {b, d, e, f} = {b, d} A C = {a, b, c, d} {a, b, e, g} = {a, b} (A B) (A C) = {b, d} {a, b} = {a, b, d} = A B A C (A B) (A C) A (B C) = (A B) (A C) • This example is left as an exercise for you.

Practice Problems 4 A B = B A A B n( ) = 0 A (B C)

Complement of a Set Definition The set of elements of U which are not elements of set A is called the complement of A. Ac or A’ ‘the complement of set A’

Complement of a Set Properties Let U be a universal set & A U. • A A’ = U • A A’ = • U’ = • (A’)’ = A ’ = U Example 14 Check

Solution 14 Complement of a Set 1. A’ = {4, 5, 8, b} • A A’ = {a, 3, 7, 9} {4, 5, 8, b} = {3, 4, 5, 7, 8, 9, a, b} = U • A A’ = {a, 3, 7, 9} {4, 5, 8, b} = • A’ = {4, 5, 8, b} (A’)’ = {a, 3, 7, 9} = A

Definition Difference of Two Sets The set of elements that are in A but not in B is called the difference of sets A and B. A-B or AB Note ‘A difference B’ Example 15 Check

Note


Difference of Two Sets Properties • A–B B– A • A– = A • (A – B) (B – A) = • A–A= • A – B = A B’ • If A B then A – B = De Morgan’s Laws If A and B are two sets, then (A B)’ = A’ B’ and (A B)’ = A’ B’. Example 16 Check


Practice Problems 5 A B = B A A B n( ) = 0 A (B C)
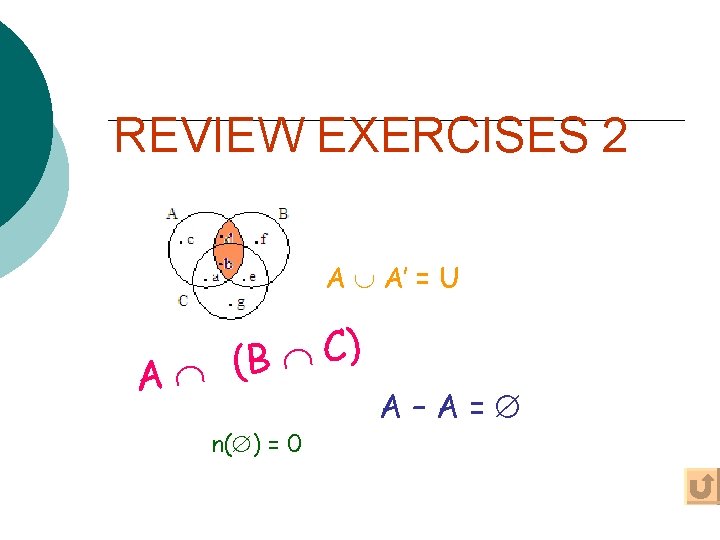
REVIEW EXERCISES 2 A A’ = U ) C B ( A n( ) = 0 A–A=