Discrete Mathematics Chapter10 Trees Introduction to Tree 10

Discrete Mathematics Chapter-10 Trees

Introduction to Tree (§ 10. 1) Def 1. A connected (undirected) graph that contains no simple circuits is called a tree. p Trees are particularly useful in computer science, where they are employed in a wide range of algorithms. p n n Construct efficient algorithms for locating items in a list. Construct efficient codes saving costs in data transmission and storage. Study games such as checkers and chess. Model procedure carried out using sequence of decisions.

The Bernoulli Family of Mathematicians Nikolaus (1623 -1708) Jacob (1654 -1705) Nikolaus (1662 1716) Johann (1667 - 1748 ) Nikolaus Daniel (1687 - 1759) (1695 -1726) (1700 - 1782) Johann (1710 - 1790) Johann (1746 -1807) Jacob (1759 1789)

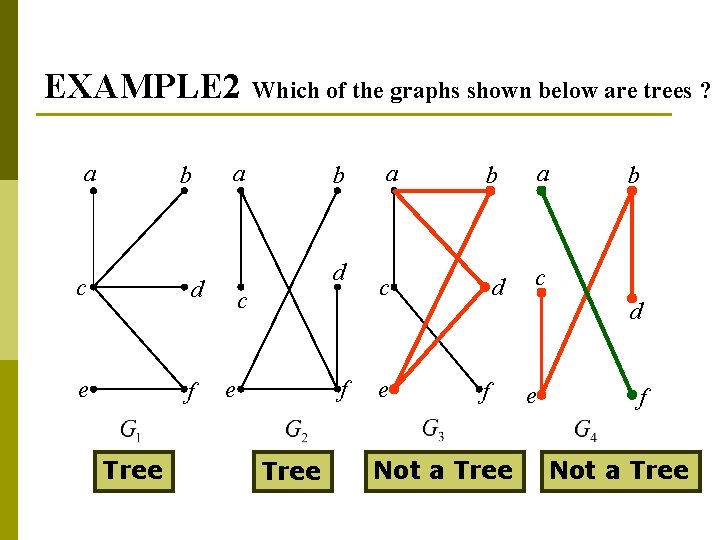
EXAMPLE 2 a b c d e f Tree Which of the graphs shown below are trees ? a b d c e f Tree a b a d c c e f Not a Tree b d e f Not a Tree

Theorem 1 p p An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices. Pf: T is a tree. T is connected, no simple circuit. For any vertices x and y, there is a simple path. If there is a different path from x to y, then two different paths will form a circuit. This is a contradiction. Thus the path is from x to y is unique. Assume that there is a unique path between any two vertices in graph T. T is connected. Suppose that T contains a simple circuit. Then every pair of vertices in this circuit, say x and y, have two different paths from x to y. That contradicts to the uniqueness of the path. Thus T has no circuit, and then T is a tree.

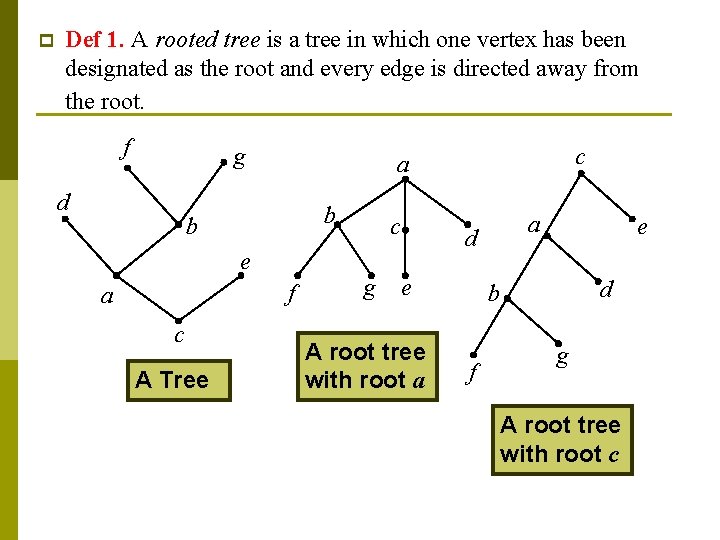
p Def 1. A rooted tree is a tree in which one vertex has been designated as the root and every edge is directed away from the root. f g d b b e f a c A Tree c a c g a d e A root tree with root a e d b f g A root tree with root c

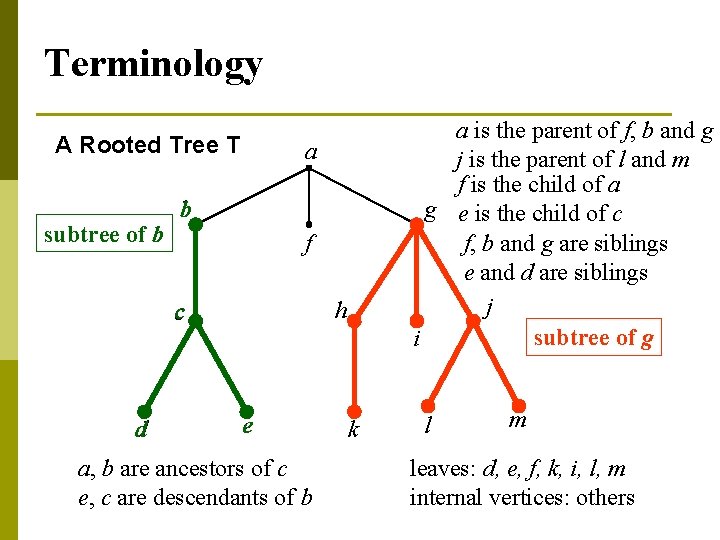
Terminology Ancestors p Descendants p parent p Child p Siblings p Leaf p Internal vertex p Subtree p

Terminology A Rooted Tree T subtree of b a b f h c d a is the parent of f, b and g j is the parent of l and m f is the child of a g e is the child of c f, b and g are siblings e and d are siblings j subtree of g i e a, b are ancestors of c e, c are descendants of b k l m leaves: d, e, f, k, i, l, m internal vertices: others

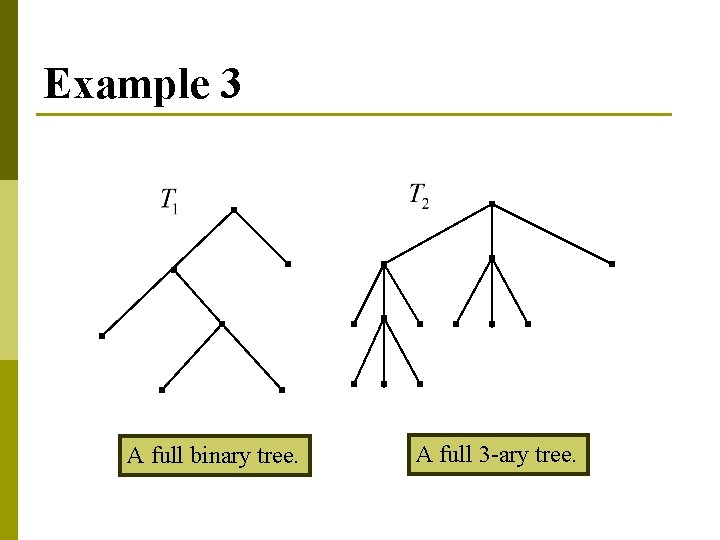
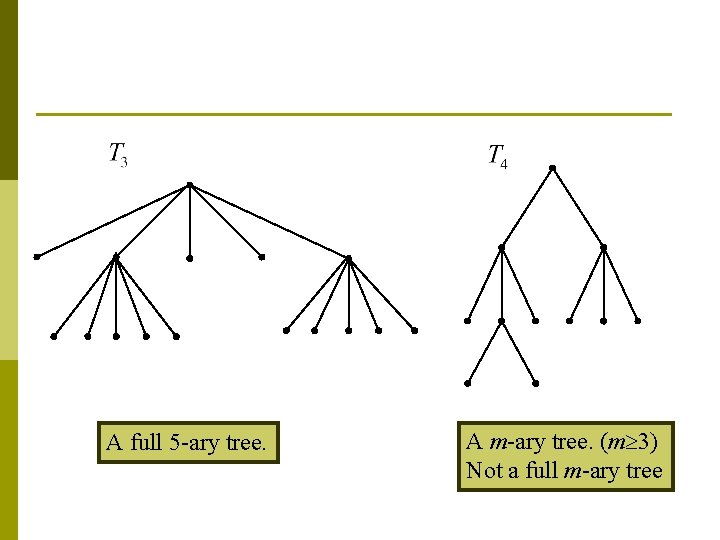
Def 3 A rooted tree is called an m-ary tree if every interval vertex has no more than m children. p The tree is called a full m-ary tree if every interval vertex has exactly m children. p An m-ary tree with m = 2 is called a binary tree. p

Example 3 A full binary tree. A full 3 -ary tree.

A full 5 -ary tree. A m-ary tree. (m 3) Not a full m-ary tree

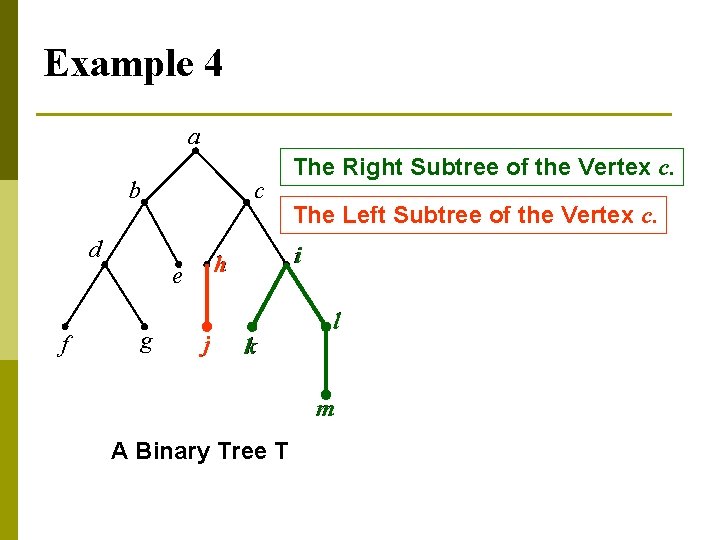
More Terminology An ordered rooted tree is a rooted tree where the children of each internal vertex are ordered (from left to right). p In an ordered binary tree (usually called just a binary tree), if an internal vertex has two children, the first child is called the left child and the second one is called the right child. p The tree rooted at the left (right) child of a vertex is called the left (right) subtree of this vertex. p

Example 4 a b d f c g j The Left Subtree of the Vertex c. i h e The Right Subtree of the Vertex c. k l m A Binary Tree T

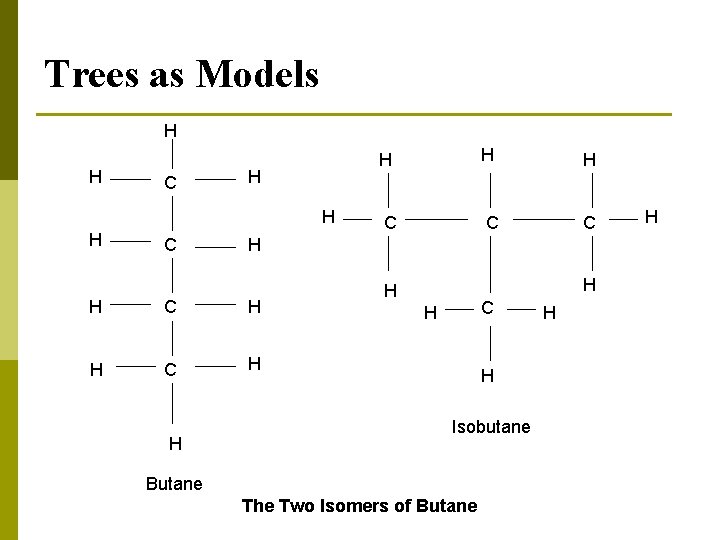
Trees as Models H H C H H H C C H H H C H H Isobutane Butane The Two Isomers of Butane H H

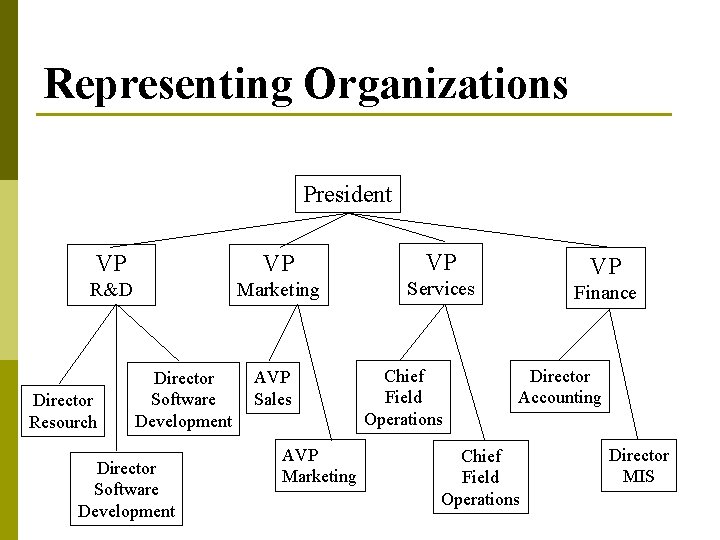
Representing Organizations President VP VP VP R&D Marketing Services Director Resourch Director Software Development AVP Sales AVP Marketing Chief Field Operations VP Finance Director Accounting Chief Field Operations Director MIS

Theorem 2 p p A tree with n verices has n 1 edges. Pf: Prove by induction. Let P(n) be the statement “A tree with n verices has n 1 edges. ” Basis Step: When n = 1, a tree with one vertex has no edge. P(1) is true. Inductive Step: Assume that P(k) is true. Suppose that T is a tree with k+1 vertices and v is a leaf. Let w is the parent of v. Remove v and the edge connecting v and w. We’ll get a tree T’ with k vertices and then has k 1 edges. It follows that T has k edges. Then P(k+1) is true.

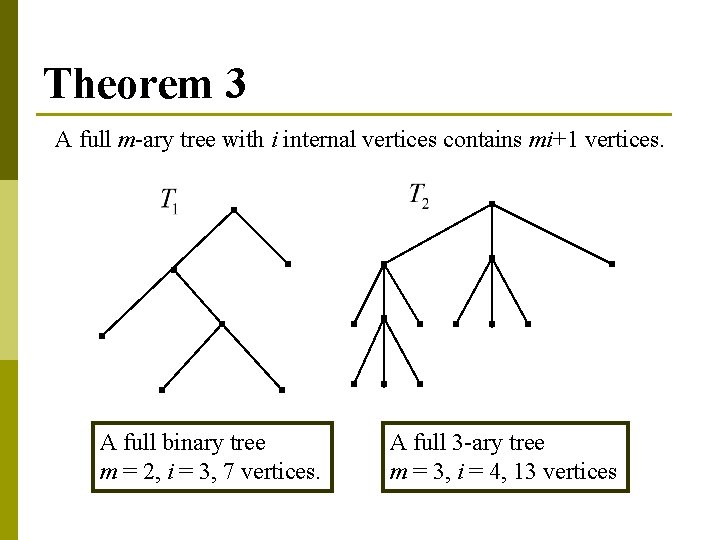
Theorem 3 A full m-ary tree with i internal vertices contains mi+1 vertices. A full binary tree m = 2, i = 3, 7 vertices. A full 3 -ary tree m = 3, i = 4, 13 vertices

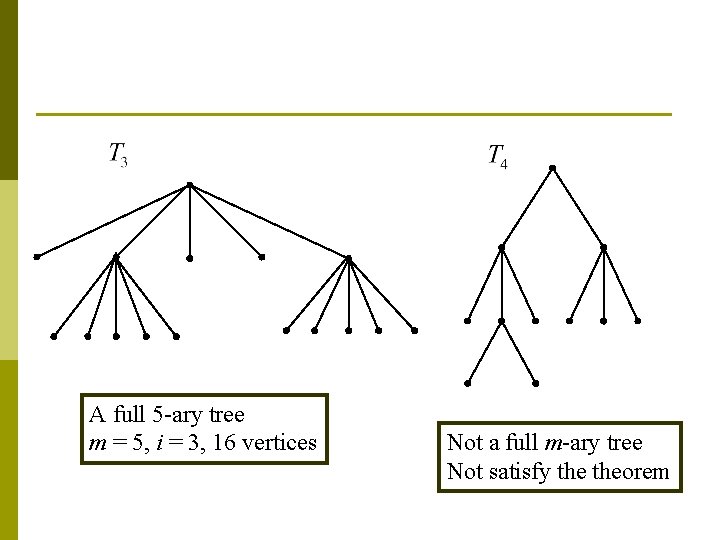
A full 5 -ary tree m = 5, i = 3, 16 vertices Not a full m-ary tree Not satisfy theorem

Example 9 p p A chain letter: Each people sends to 4 people. Some people do this, but others do not send any letters. How many people have seen this letter, including the first person, if no one receives more than one letter and if the chain letter ends after there have 100 people who read it but didn’t send it out? How many people sent out the letter? Sol: This is a 4 -ary (m = 4) tree. Note there are n = mi +1 vertices and l = n i leaves. 100(= l) leaves n = 4(n 100) + 1 400 1 = 3 n There are n = 133 vertices. There are 133 100 = 33 internal vertices.

Theorem 4 p 1. 2. 3. A full m-ary tree with n vertices has i = (n 1)/m internal vertices and l = [(m 1)n + 1]/m leaves, i interval vertices has n = mi + 1 vertices and l = (m 1)i + 1 leaves , l leaves has n = (ml 1)/(m 1) vertices and i = (l 1)/(m 1) internal vertices.

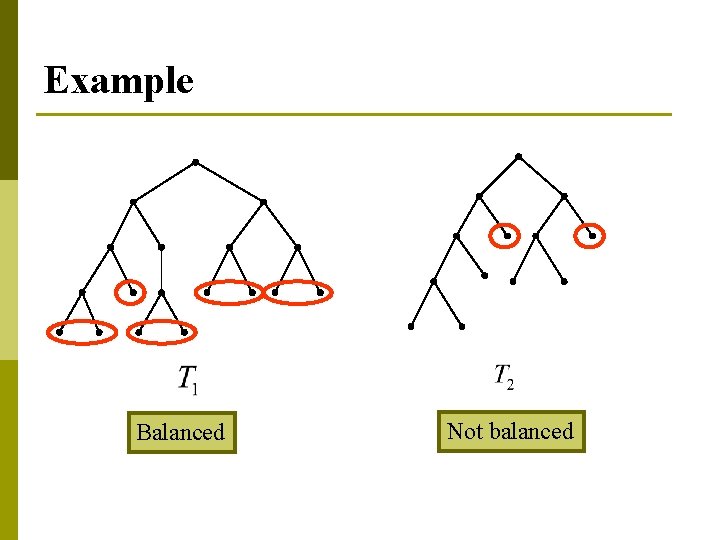
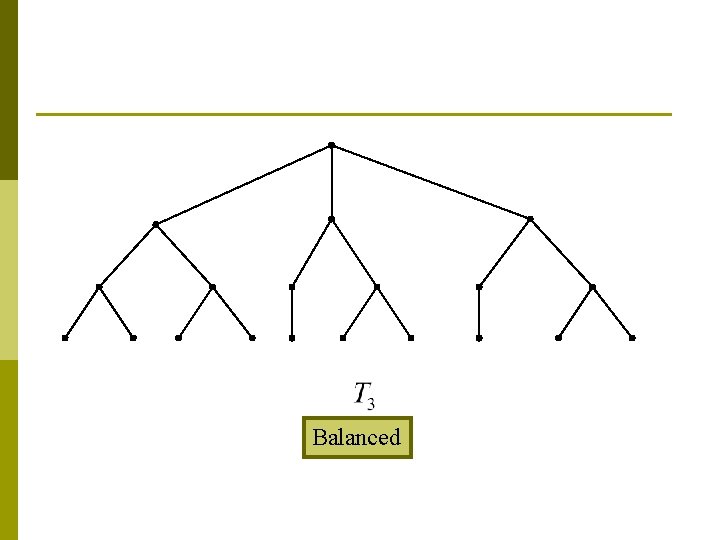
More Terminology p The level of a vertex v in a rooted tree is the length of the unique path from the root to this vertex v. n p The height of a rooted tree is the maximum of the levels of vertices. n p The level of the root is defined to be zero. That is, the height is the length of the longest path from the root to any vertex. A rooted m-ary tree of height h is balanced if all leaves are at levels h or h 1.

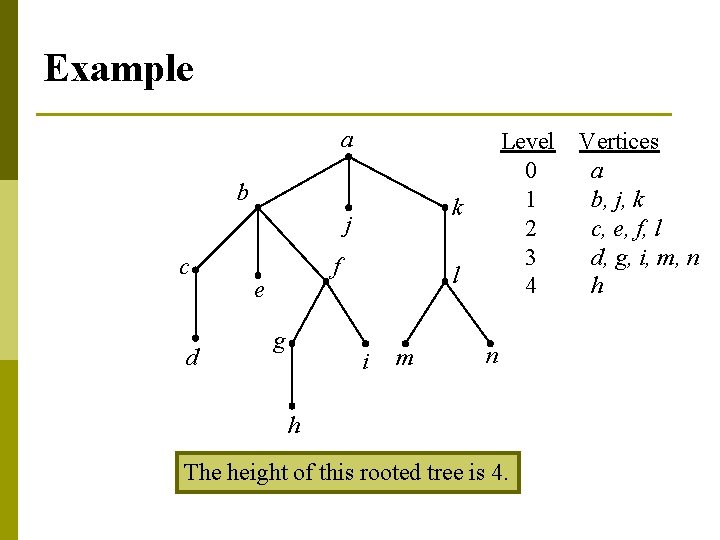
Example a b k j c d f e g Level 0 1 2 3 4 l i m n h The height of this rooted tree is 4. Vertices a b, j, k c, e, f, l d, g, i, m, n h

Example Balanced Not balanced

Balanced

10. 2 Applications of Trees

Introduction How should items in a list be stored so that an item can be easily located ? p What series of decisions should be made to find an object with a certain property in a collection of objects of a certain type ? p How should a set of characters be efficiently coded by bit strings ? p

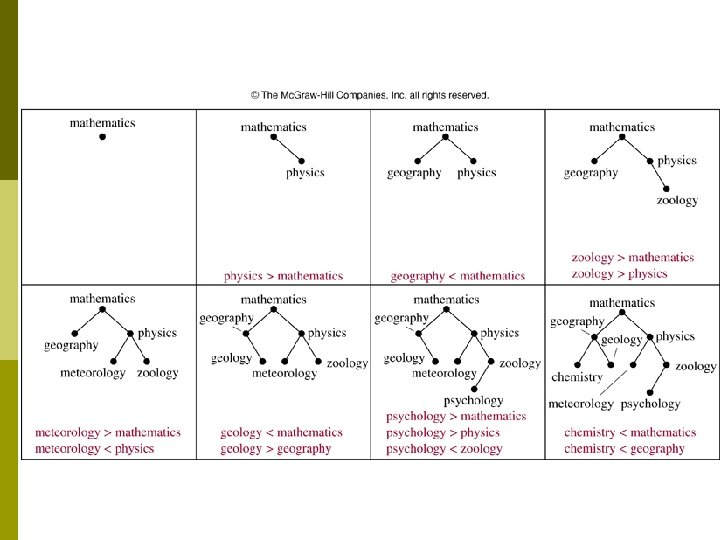
Example 1 p Form a binary search tree for the words mathematic , physics , geography , zoology , meteorology , geology , psychology , and chemistry (using alphabetical order)

Constructing a Binary Search Tree 按照題目所給的字順序排，如題Mathematics就是 root p 接下Physic>Mathematics，所以在M右下加一個 child p Geography<Mathematics，所以再M左下加一個 child p Zoology>Mathematics且>Physics，所以再P右下加 一個child p Meteorology>Mathematics但<Physics，所以在P左 下加一個child p

Geology<Mathematics但>Geography，所以在 Geography的右下加一個child p Psychology>Mathematics且>Physics但<Zoology所 以在Z左下加一個child p Chemistry<Mathematics且<Geography，所以在 Geography的左下加一個child p

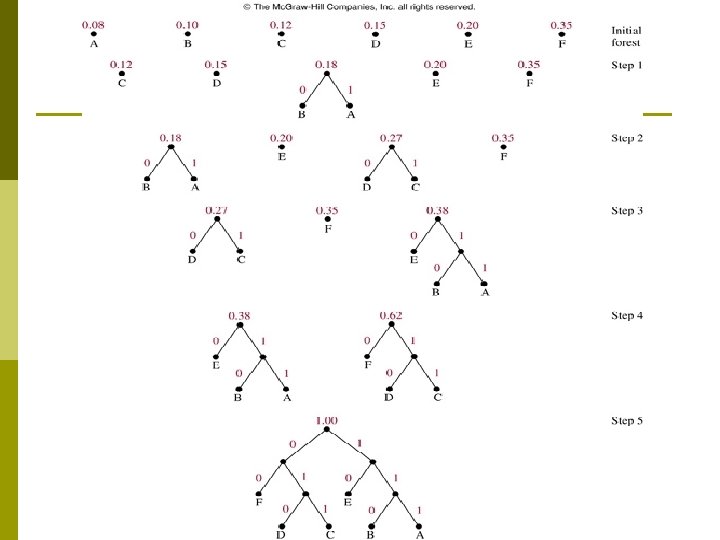
Example 5 p Use Huffman coding to encode the fallowing symbols with the frequencies listed: A: 0. 08, B: 0. 10, C: 0. 12, D: 0. 15, E: 0. 20, F: 0. 35. What is the average number of bits used to encode a character ?

9. 3 Tree Traversal

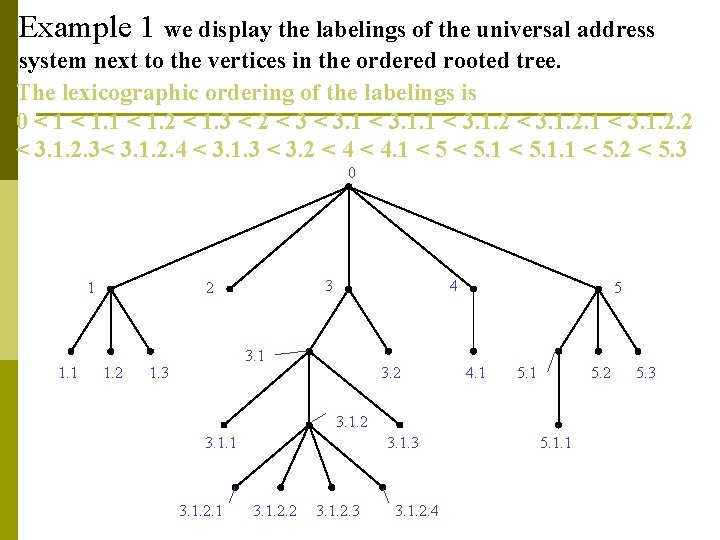
Universal address system We will describe one way to order totally the vertices of an ordered rooted tree. To produce this ordering, we must first label all the vertices. We do this recursively : 1. Label the root with the integer 0. Then label its k children (at label 1) from left to right with 1, 2, . . . , k. 2. For each vertex v at level n with label A, label its k v children, as they are drawn from left to right, with A. 1, A. 2, …A. k v.

Example 1 we display the labelings of the universal address system next to the vertices in the ordered rooted tree. The lexicographic ordering of the labelings is 0 < 1. 1 < 1. 2 < 1. 3 < 2 < 3. 1. 2. 1 < 3. 1. 2. 2 < 3. 1. 2. 3< 3. 1. 2. 4 < 3. 1. 3 < 3. 2 < 4. 1 < 5. 1. 1 < 5. 2 < 5. 3 0 1 1. 1 3 2 1. 2 4 3. 1 1. 3 3. 2 5 4. 1 5. 2 5. 1 3. 1. 2 3. 1. 1 3. 1. 2. 1 3. 1. 3 3. 1. 2. 2 3. 1. 2. 3 3. 1. 2. 4 5. 1. 1 5. 3

Definition 1 Let T be an order rooted tree with root r. If T consists only of r , then r is the preorder traversal of T. Otherwise , suppose that T 1 , T 2 , … , Tn are the subtree at r from left to right in T. The preorder traversal begins by visiting r. It continues by traversing T 1 in preorder , then T 2 in preorder , and so on , until Tn is traversed in preorder.

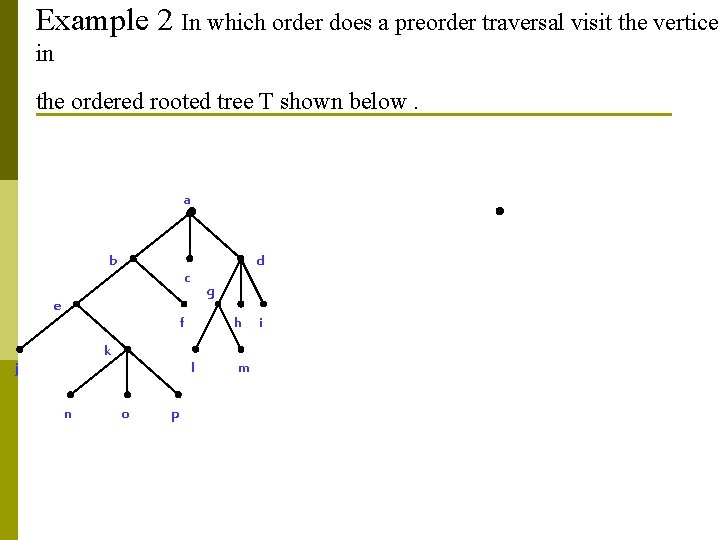
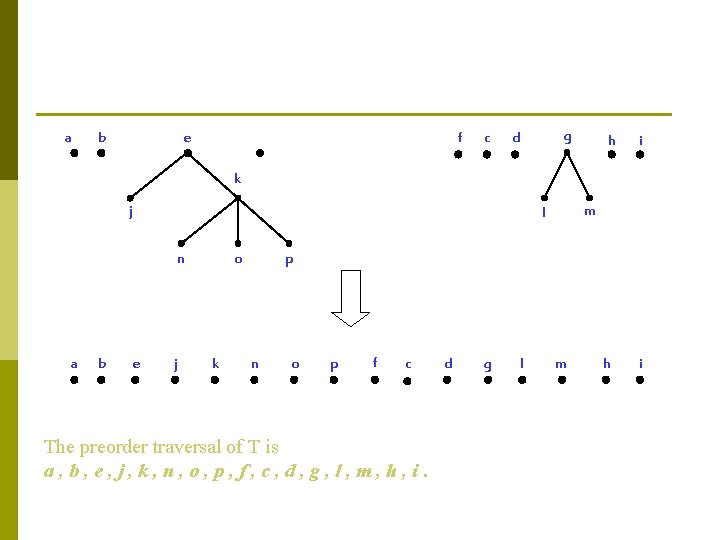
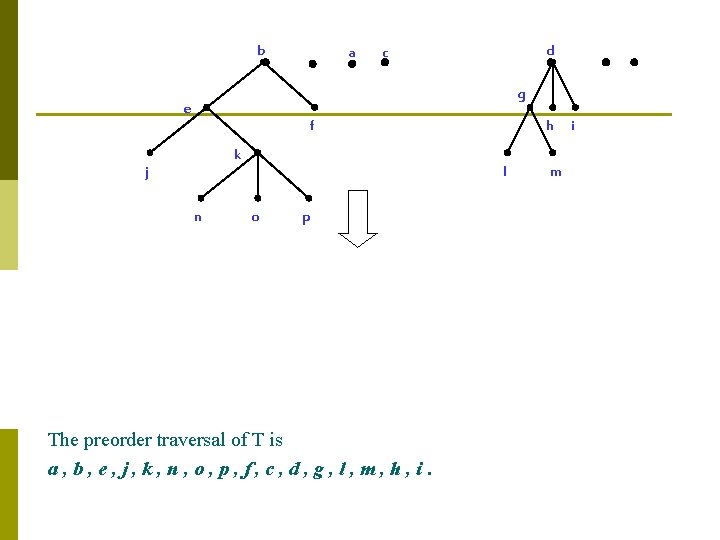
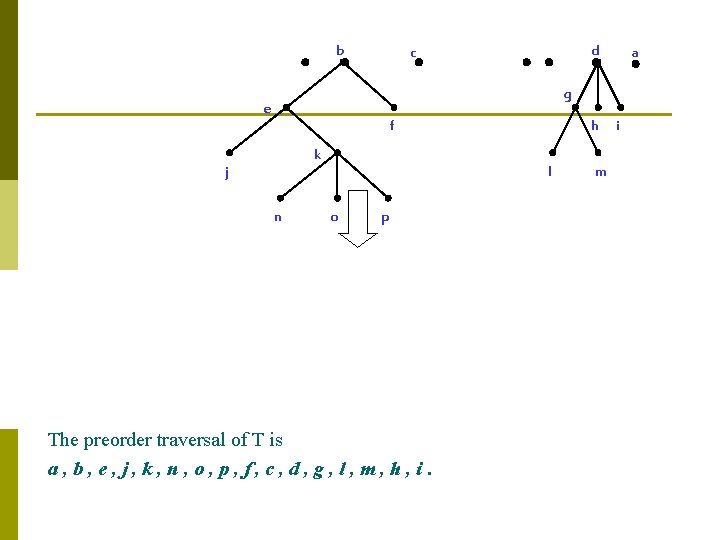
Example 2 In which order does a preorder traversal visit the vertices in the ordered rooted tree T shown below. a b d c e g f k j n h l o p m i

a b e f c g d h i k j n a b e m l j o k p n o p f c The preorder traversal of T is a, b, e, j, k, n, o, p, f, c, d, g, l, m, h, i. d g l m h i

Definition 2 Let T be an ordered rooted tree with root r. If T consists Only of r , then r is the inorder traversal of T. Otherwise , suppose that T 1 , T 2 , … , Tn are the subtree at r from left to right in T. The inorder traversal begins by traversing T 1 in inorder , then visiting r. It continues by traversing T 2 in inorder , then T 3 in inorder , …, and finally Tn in inorder.

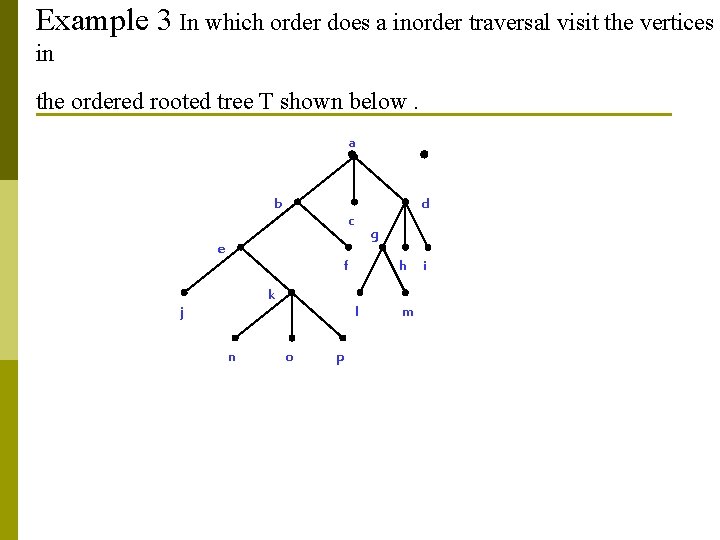
Example 3 In which order does a inorder traversal visit the vertices in the ordered rooted tree T shown below. a b d c e g f k j n h l o p m i

b f n n h k j e d c g e j a o k o l i m p b f a c l p The preorder traversal of T is a, b, e, j, k, n, o, p, f, c, d, g, l, m, h, i. g m d h i

Definition 3 Let T be an ordered rooted tree with root r. If T Consists only of r , then r is the postrder traversal of T. Otherwise , suppose that T 1 , T 2 , … , Tn are the subtreesat r from left to right in T. The postorder traversal begins by traversing T 1 in postorder , then T 2 in inorder , then T 3 in inorder , …, and ends by visiting r.

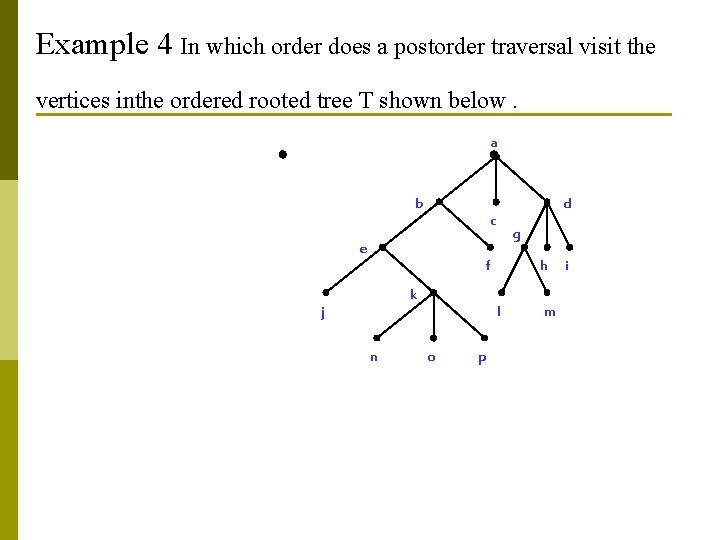
Example 4 In which order does a postorder traversal visit the vertices inthe ordered rooted tree T shown below. a b d c e g f k j n h l o p m i

b f n k n o h k j e a g e j d c b l o f i m p a c l p The preorder traversal of T is a, b, e, j, k, n, o, p, f, c, d, g, l, m, h, i. g m d h i

INFIX, PREFIX, AND POSTFIX NOTATION

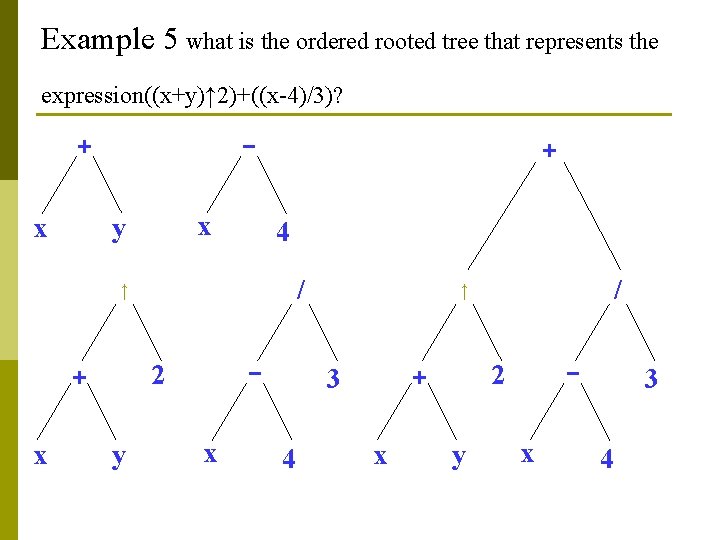
Example 5 what is the ordered rooted tree that represents the expression((x+y)↑ 2)+((x-4)/3)? _ + x x y + 4 / ↑ 2 + x _ y x x _ 2 + 3 4 / ↑ y x 3 4

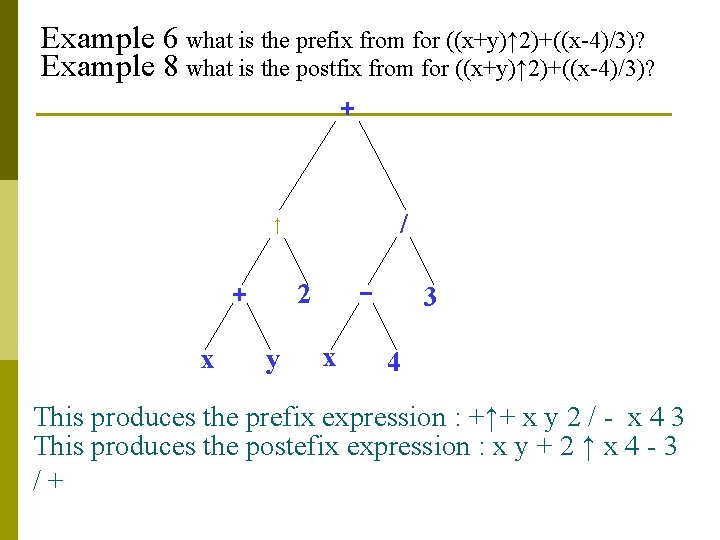
Example 6 what is the prefix from for ((x+y)↑ 2)+((x-4)/3)? Example 8 what is the postfix from for ((x+y)↑ 2)+((x-4)/3)? + / ↑ x _ 2 + y x 3 4 This produces the prefix expression : +↑+ x y 2 / - x 4 3 This produces the postefix expression : x y + 2 ↑ x 4 - 3 /+

Example 7 what is the value of the prefix expression +-*235/↑ 234? + - * 2 3 5 / ↑ 2 3 4 + - * 2 3 5 / 8 4 + - * 2 3 5 2 + - 6 5 2 + 1 2 3

Example 9 what is the value of the postfix expression 7 2 3 * - 4 ↑ 9 3 / + ? 7 2 3 * - 4 ↑ 9 3 / + 7 6 - 4 ↑ 9 3 / + 1 3 + 4

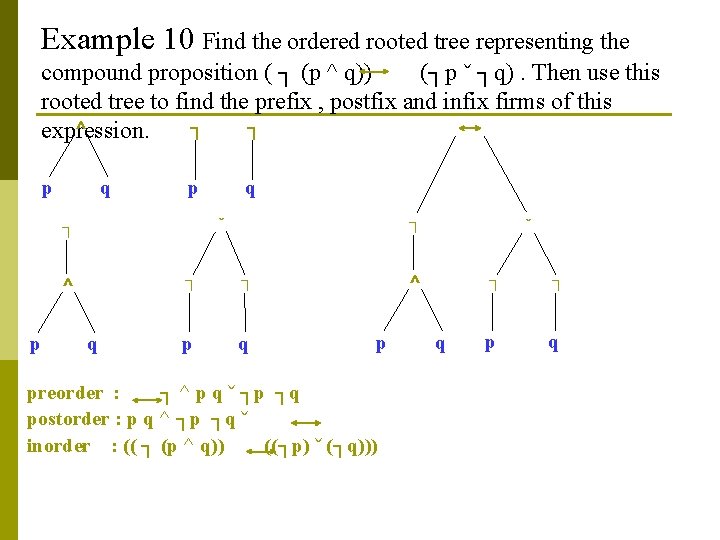
Example 10 Find the ordered rooted tree representing the compound proposition ( ┐ (p ^ q)) (┐p ˇ ┐q). Then use this rooted tree to find the prefix , postfix and infix firms of this ┐ ┐ ^ expression. p q p ┐ ˇ ┐ ^ p q q ┐ ┐ p q ˇ ^ p preorder : ┐ ^ p q ˇ ┐p ┐q postorder : p q ^ ┐p ┐q ˇ inorder : (( ┐ (p ^ q)) ((┐p) ˇ (┐q))) q ┐ ┐ p q