Discrete Mathematics Chapter 7 Advanced Counting Techniques Lingling












































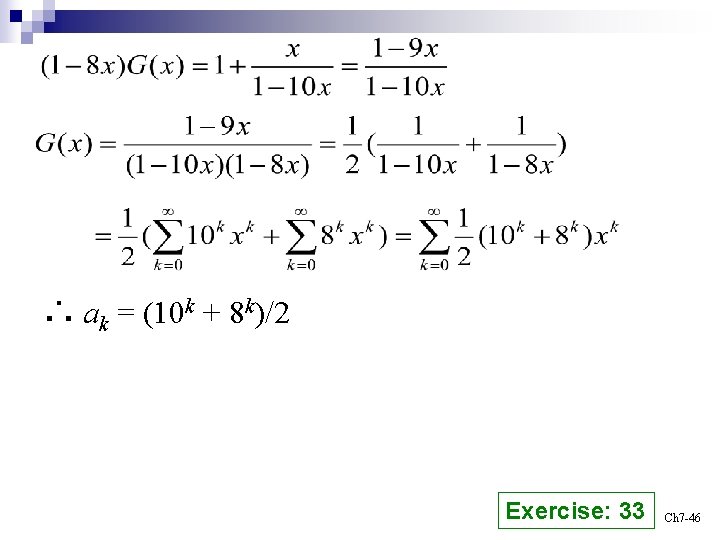










- Slides: 56

Discrete Mathematics Chapter 7 Advanced Counting Techniques 大葉大學 資訊 程系 黃鈴玲(Lingling Huang)

Outline n n n 7. 1 Recurrence Relations 7. 2 Solving Linear Recurrence Relations 7. 4 Generating Functions 7. 5 Inclusion-Exclusion 7. 6 Applications of Inclusion-Exclusion Ch 9 -2

7. 1 Recurrence Relations(遞迴關係 ) Example 1. Let {an} be a sequence that satisfies the recurrence relation an=an-1 -an-2 for n=2, 3, …, and suppose that a 0=3, and a 1=5. Here a 0=3 and a 1=5 are the initial conditions. By the recurrence relation, a 2 = a 1 -a 0 = 2 a 3 = a 2 -a 1 = -3 a 4 = a 3 -a 2 = -5 : Q 1: Applications ? Q 2: Are there better ways for computing the terms of {an}? Ch 7 -3 n

※Modeling with Recurrence Relations We can use recurrence relations to model (describe) a wide variety of problems. Example 3. Compound Interest (複利) Suppose that a person deposits(存款) $10000 in a saving account at a bank yielding 11% per year with interest compounded annually. How much will be in the account after 30 years ? Sol : Let Pn denote the amount in the account after n years. P 0=10000 Pn=Pn-1 + 0. 11 Pn-1=1. 11 Pn-1, ∴ P 30=1. 11 P 29=(1. 11)2 P 28=…=(1. 11)30 P 0 =228922. 97 Ch 7 -4

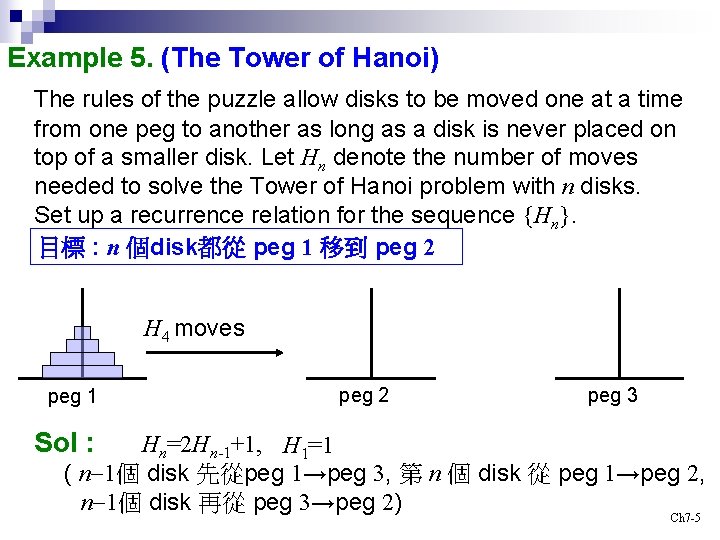
Example 5. (The Tower of Hanoi) The rules of the puzzle allow disks to be moved one at a time from one peg to another as long as a disk is never placed on top of a smaller disk. Let Hn denote the number of moves needed to solve the Tower of Hanoi problem with n disks. Set up a recurrence relation for the sequence {Hn}. 目標 : n 個disk都從 peg 1 移到 peg 2 H 4 moves peg 1 Sol : peg 2 peg 3 Hn=2 Hn-1+1, H 1=1 ( n-1個 disk 先從peg 1→peg 3, 第 n 個 disk 從 peg 1→peg 2, n-1個 disk 再從 peg 3→peg 2) Ch 7 -5

上例中 Hn=2 Hn-1+1, H 1=1 ∴Hn=2 Hn-1+1 =2(2 Hn-2+1)+1 =22 Hn-2+2+1 =22(2 Hn-3+1)+2+1 =23 Hn-3+(22+2+1) : =2 n-1 H 1+(2 n-2+2 n-3+…+1) =2 n-1+2 n-2+…+1 = =2 n-1 Ch 7 -6

Example 6. Find a recurrence relation and give initial conditions for the number of bit strings of length n that do not have two consecutive 0 s. How many such bit strings are there of length 5 ? Sol : Let an be the number of bit strings of length n that do not have two consecutive 0 s. 1 2 … n-3 n-2 n-1 1 an-1 種 an-2 種 n 1 0 ∴ an = an-1+an-2, n 3 a 1=2 (string : 0, 1) a 2=3 (string : 01, 10, 11) ∴ a 3=a 2+a 1=5, a 4=8, a 5=13 Ch 7 -7

Example 7. (Codeword enumeration) A computer system considers a string of decimal digits a valid codeword if it contains an even number of 0 digits. Let an be the number of valid n-digit codewords. Find a recurrence relation for an. Sol : 1 2 3 … n-1 an-1 種 10 n-1 - an-1 種 n 1~9 ∴ an = 9 an-1 + (10 n-1 -an-1) = 8 an-1 + 10 n-1 , n 2 a 1 = 9 0 Ch 7 -8

求an通解 : Exercise : 3, 25, 27, 29, 41 (41推廣成n) Ch 7 -9

7. 2 Solving Recurrence Relations Def 1. A linear homogeneous recurrence relation of degree k (i. e. , k terms) with constant coefficients is a recurrence relation of the form an = c 1 an-1+c 2 an-2+…+ckan-k where ci R and ck≠ 0 Example 1 and 2. fn = fn-1 + fn-2 an = an-5 an = an-1 + an-22 an = nan-1 Hn = 2 Hn-1 + 1 (True, deg=2) (True, deg=5) (False, not linear) (False, not homogeneous) Ch 7 -10

Solving Linear Homogeneous Recurrence Relations with Constant Coefficients Theorem 1. Let an = c 1 an-1+ c 2 an-2 be a recurrence relation with c 1, c 2 R. If r 2 - c 1 r - c 2= 0 (稱為characteristic equation) has two distinct roots r 1 and r 2. Then the solution of an is an = a 1 r 1 n + a 2 r 2 n , for n=0, 1, 2, …, where a 1 , a 2 are constants. (a 1 , a 2可利用 a 0, a 1算出) Ch 7 -11

Example 3. What’s the solution of the recurrence relation an = an-1 + 2 an-2 with a 0=2 and a 1=7 ? Sol : The characteristic equation is r 2 – r - 2=0. Its two roots are r 1= 2 and r 2 = -1. r 與r 順序可交換, Hence an=a 1 2 n +a 2 (-1)n. 結果會一樣 ∵a 0 = a 1+a 2 = 2, a 1=2 a 1 -a 2=7 ∴a 1 = 3, a 2 = -1 驗算:a 2 = a 1 + 2 a 0 =11 a 2= 3 22 - 1 =11 an = 3 2 n - (-1)n. 1 2 Ch 7 -12

Example 4. Find an explicit formula for the Fibonacci numbers. Sol : fn = fn-1 + fn-2 , n 2, f 0=0 , f 1=1. The characteristic equation is r 2 - r - 1=0. Its two roots are So we have , . Ch 7 -13

Thm 2. Let an = c 1 an-1+c 2 an-2 be a recurrence relation with c 1, c 2 R. If r 2 - c 1 r - c 2= 0 has only one root r 0. Then the solution of an is an = a 1 r 0 n + a 2 n r 0 n for n=0, 1, 2, …, where a 1 and a 2 are constants. Ch 7 -14

Example 5. What’s the solution of an= 6 an-1 - 9 an-2 with a 0=1 and a 1=6 ? Sol : The root of r 2 - 6 r + 9 = 0 is r 0 = 3. Hence an = a 1.3 n +a 2.n.3 n. ∵a 0 = a 1 = 1 a 1 = 3 a 1 + 3 a 2 = 6 ∴ a 1 = 1 and a 2 = 1 驗算:a 2 = 6 a 1 - 9 a 0 =27 n n an = 3 + n.3 a 2= 32 +2 32 =27 Ch 7 -15

Thm 3. Let an = c 1 an-1 + c 2 an-2 + … + ckan-k be a recurrence relation with c 1, c 2, …, ck R. If rk - c 1 rk-1 - c 2 rk-2 -…- ck = 0 has k distinct roots r 1, r 2, …, rk. Then the solution of an is an = a 1 r 1 n +a 2 r 2 n + …+akrkn, for n = 0, 1, 2, … where a 1, a 2, …ak are constants. Ch 7 -16

Example 6 (k = 3) Find the solution of an = 6 an-1 - 11 an-2 + 6 an-3 with initial conditions a 0=2, a 1=5 and a 2=15. Sol : The roots of r 3 - 6 r 2 + 11 r – 6 = 0 are r 1 = 1, r 2 = 2, and r 3 = 3 ∴an = a 1 1 n + a 2 2 n + a 3 3 n ∵a 0 = a 1 + a 2 + a 3 = 2 a 1 = 1, a 2 = -1, a 1 = a 1 + 2 a 2 + 3 a 3 = 5 a 3 = 2 a 2 = a 1 + 4 a 2 + 9 a 3 = 15 0 =47 ∴an = 1 - 2 n + 2 3 n 驗算:a 3 = 6 a 2 -311 a 1+ 6 a 3 a 3= 1 - 2 + 2 3 =47 Ch 7 -17

Thm 4. Let an = c 1 an-1 + c 2 an-2 + … + ckan-k be a recurrence relation with c 1, c 2, …, ck R. If rk - c 1 rk-1 - c 2 rk-2 - … - ck = 0 has t distinct roots r 1, r 2, …, rt with multiplicities m 1, m 2, …, mt respectively, where mi 1, i, and m 1+ m 2 +…+ mt = k, then where ai, j are constants for 1 i t and 0 j mi-1. Ch 7 -18


Example 8. Find the solution to the recurrence relation an = -3 an-1 - 3 an-2 - an-3 with initial conditions a 0 = 1, a 1 = -2 and a 2 = -1. Sol : r 3 + 3 r 2 + 3 r + 1 = 0 has a single root r 0 = -1 of multiplicity three. ∴ an = (a 1+a 2 n+a 3 n 2) r 0 n = (a 1+a 2 n+a 3 n 2)(-1)n ∵ a 0 = a 1 = 1 a 1 = (a 1+a 2+a 3) (-1) = -2 a 2 = a 1+2 a 2+4 a 3 = -1 驗算:a 3 = - 3 a 2 - 3 a 1 - a 0 =8 a 3= (1+3 3 -2 32) (-1)3 =8 ∴a 1 = 1, a 2 = 3, a 3 = -2 an = (1+3 n-2 n 2) (-1)n Exercise : 3, 15, 19 Ch 7 -20

Linear Nonhomogeneous Recurrence Relations with Constant Coefficients Example: an = 3 an-1 + 2 n A recurrence relation of the form an = c 1 an-1 + c 2 an-2 + … + ckan-k + F(n), where c 1, c 2, …, ck are real numbers and F(n) is a function not identically zero depending only on n. The recurrence relation an = c 1 an-1 + c 2 an-2 + … + ckan-k is called the associated homogeneous recurrence relation. Ch 7 -21

Example 9: an = an-1 + 2 n, associated h. r. r an = an-1 + an-2 + n 2+1, associated h. r. r an = an-1 + an-2 an = 3 an-1 + n 3 n, associated h. r. r an = 3 an-1 an = an-1 + an-3 + n!, associated h. r. r an = an-1 + an-3 Ch 7 -22

Theorem 5. If {an (p)} is a particular solution (特解) of an = c 1 an-1 + c 2 an-2 + … + ckan-k + F(n), then every solution is of the form {an (p) + an (h)}, where {an (h)} is a solution of an = c 1 an-1 + c 2 an-2 + … + ckan-k Proof. If {an (p)} and {bn} are both solutions of an = c 1 an-1 + c 2 an-2 + … + ckan-k + F(n), then an(p) = c 1 an-1(p) + c 2 an-2 (p)+ … + ckan-k(p) + F(n), and bn = c 1 bn-1 + c 2 bn-2 + … + ckbn-k + F(n). an(p) - bn = c 1(an-1 - bn-1) + c 2(an-2 - bn-2) + … + ck(an-k - bn-k) {an(p) - bn} is a solution of an = c 1 an-1 + c 2 an-2 + … + ckan-k bn = an(p) + an (h) Ch 7 -23

Example 10. Find all solutions of the recurrence relation an = 3 an-1 + 2 n. What is the solution with a 1=3? Sol : {associated的部分 an = 3 an-1 先解} Characteristic equation: r – 3 = 0 r = 3 an(h) = a 3 n. {particular solution} ∵ F(n) = 2 n ∴ Let an(p) =cn+d, where c, d R. If an(p) = cn+d is a solution to an = 3 an-1 + 2 n, then cn+d = 3(c(n-1)+d)+2 n =3 cn - 3 c + 3 d +2 n 2 cn-3 c + 2 d +2 n = (2 c+2)n + (2 d-3 c) = 0 (任何n代入都需為 0) ∴ 2 c+2 = 0, and 2 d-3 c = 0 c = -1, d = -3/2 an(p) = -n - 3/2 an = an(h) +an(p) = a 3 n-n - 3/2 If a 1= a 3 -1 - 3/2 = 3 a = 11/6 an = (11/6) 3 n- n - 3/2 Ch 7 -24

Example 11. Find all solutions of the recurrence relation an = 5 an-1 -6 an-2 + 7 n. Sol : {associated的部分 an = 5 an-1 -6 an-2 先解} Characteristic equation: r 2 – 5 r + 6 = 0 r 1 = 3, r 2 = 2 an(h) = a 1 3 n + a 2 2 n. {particular solution} ∵ F(n) = 7 n ∴ Let an(p) = c 7 n, where c R. If an(p) = c 7 n is a solution to an = 5 an-1 -6 an-2 + 7 n, then c 7 n = 5 c 7 n-1 - 6 c 7 n-2 + 7 n 49 c = 35 c - 6 c + 49 Exercise : 23 c = 49/20 an(p) = (49/20) 7 n an = an(h) +an(p) = a 1 3 n + a 2 2 n + (49/20) 7 n Ch 7 -25

Theorem 6. an = c 1 an-1 + c 2 an-2 + … + ckan-k + F(n), where F(n) = (btnt + bt-1 nt-1 +…+ b 1 n + b 0)sn. When s is not a root of the characteristic equation of the associated linear homogeneous recurrence relation, there is a particular solution of the form (ptnt + pt-1 nt-1 +…+ p 1 n + p 0)sn. When s is a root of the characteristic equation and its multiplicity is m, there is a particular solution of the form nm(ptnt + pt-1 nt-1 +…+ p 1 n + p 0)sn. Ch 7 -26

Example 12. What form does a particular solution of the linear nonhomogeneous recurrence relation an = 6 an-1 - 9 an-2 + F(n) have when F(n) =3 n, F(n) =n 22 n , and F(n) = (n 2+1)3 n. Sol : The associated linear homogeneous recurrence relation is an = 6 an-1 - 9 an-2. characteristic equation: r 2 - 6 r + 9 = 0 r = 3 (2重根) F(n) =3 n, and 3 is a root an(p) = p 0 n 23 n F(n) =n 3 n, and 3 is a root an(p) = n 2(p 1 n+p 0) 3 n F(n) =n 22 n , and 2 is not a root an(p) = (p 2 n 2+p 1 n+p 0)2 n F(n) = (n 2+1)3 n , and 3 is a root an(p) = n 2 (p 2 n 2+p 1 n+p 0) 3 n Exercise : 27 Ch 7 -27

Example 13. Find the solutions of the recurrence relation an = an-1 + n with a 1=1. Sol : The associated linear homogeneous recurrence relation is an = an-1. characteristic eq. : r - 1 = 0 r = 1 an(h) = c(1)n=c F(n) = n(1)n, and 1 is a root an(p) = n(p 1 n+p 0)1 n = p 1 n 2+p 0 n 將an(p)代入an = an-1 + n p 1 n 2+p 0 n = p 1(n-1)2+p 0(n-1)+n (2 p 1 -1)n+p 0 -p 1=0 p 1= ½, an(p) = (n 2+n)/2 an = an(p) + an(h) = (n 2+n)/2+c p 0 = p 1= ½ Exercise : 29 a 1=1 c=0 an = an(p) + an(h) = (n 2+n)/2 Ch 7 -28

ex 40: Solve the simultaneous recurrence relations an = 3 an-1 + 2 bn-1 bn = an-1 + 2 bn-1 with a 0 = 1 and b 0 = 2. Sol : an -bn= 2 an-1 bn = an-2 an-1 an = 3 an-1 + 2 bn-1 = 3 an-1 + 2 an-1 - 4 an-2 an = 5 an-1 - 4 an-2 r 2 - 5 r + 4 = 0 r = 1, 4 an = a 1+a 24 n a 0 = a 1+a 2 = 1 a 1 = a 1+4 a 2 = 3 a 0 + 2 b 0 = 7 a 1 = -1, a 2 = 2 an= 2 4 n-1 bn = an-2 an-1= 2 4 n-1 -4 n+2 = 4 n+1 Ch 7 -29

7. 4 Generating Functions. Def 1. The generating function for the sequence a 0, a 1, a 2, … of real numbers is the infinite series G(x) = a 0 + a 1 x +… + anxn +… = (若數列{an} 是finite,可視為是infinite,但後面的項都 等於 0) Ch 7 -30

Example 1. Find the generating functions for the sequences {ak} with (1) ak= 3 (2) ak = k+1 (3) ak = 2 k Sol : (1) G(x) = (2) G(x) = (3) G(x) = Ch 7 -31

Example 2. What is the generating function for the sequence 1, 1, 1, 1 ? a 0 a 1 a 2 a 3 a 4 a 5 a 6及之後都=0 Sol : G(x) = = a 0 + a 1 x + a 2 x 2 + a 3 x 3 +… (expansion,展開式) (closed form) Exercise : 2 Ch 7 -32

Example 3. Let m Z+ and , for k = 0, 1, …, m. What is the generating function for the sequence a 0, a 1, …, am ? Sol : G(x) = a 0 + a 1 x + a 2 x 2 + … + amxm = (1+x)m (by下面的二項式定理) Ch 7 -33

Useful Facts About Power Series Example 4. The function f (x) = is the generating function of the sequence 1, 1, 1, …, because when |x| < 1. = 1 + x 2 + …= Example 5. The function f (x) = is the generating function of the sequence 1, a, a 2, …, because = 1 + ax + a 2 x 2 + …= when |ax| < 1 for a≠ 0. Exercise : 5(a)(b), 11(a) Ch 7 -34

Theorem 1. Let f(x) = and g(x) = Then f(x) + g(x) = . . f(x) g(x) = (a 0+a 1 x+a 2 x 2 +…)(b 0+b 1 x +b 2 x 2+…) = (a 0 b 0)+(a 0 b 1+a 1 b 0) x+(a 0 b 2+a 1 b 1+a 2 b 0) x 2+… = Ch 7 -35

Example 6. Let f (x) = . Use Example 4 to find the coefficients a 0, a 1, a 2, … in the expansion f (x)= . Sol : = 1 + x 2 + … = = ak = k+1 Ch 7 -36

Def 2. Let u R and k N. Then the extended binomial coefficient Example 7. Find Sol : is defined by and Ch 7 -37

Example 8 When the top parameter is a negative integer, the extended binomial coefficient can be expressed in terms of an ordinary binomial coefficient. Ch 7 -38

Thm 2. (The Extended Binomial Theorem) Let x R with |x|<1 and let u R, then Ch 7 -39

Example 9. (跳過) Find the generating functions for (1+x)-n and (1 -x)-n where n Z+ Sol : By the Extended Binomial Theorem, By replacing x by –x we have Exercise : 11(b)(d) Ch 7 -40

Counting Problems and Generating Functions Generating functions can be used to count the number of combinations of various types. Example 10. Find the number of solutions of e 1 + e 2 + e 3 = 17, where e 1, e 2, e 3 are integers with 2 e 1 5, 3 e 2 6, and 4 e 3 7. Sol : The number of solutions with the indicated constraints is the coefficient of x 17 in the expansion of (x 2 + x 3 + x 4 + x 5)(x 3 + x 4 + x 5 + x 6)(x 4 + x 5 + x 6 + x 7) (即相當於找 e 1, e 2, e 3 使 xe xe xe = x 17) 1 2 3 (e 1, e 2, e 3)=(4, 6, 7), (5, 5, 7), (5, 6, 6) 共 3種 Ch 7 -41

Example 11. In how many different ways can eight identical cookies be distributed among three distinct children if each child receives at least two cookies and no more than four cookies? Sol : The number of solutions is the coefficient of x 8 in the expansion of (x 2 + x 3 + x 4)3 (c 1, c 2, c 3) = (2, 2, 4), (2, 3, 3), (2, 4, 2), (3, 2, 3), (3, 3, 2), (4, 2, 2) 共 6種 Exercise: 23 Ch 7 -42

※Using Generating Functions to solve Recurrence Relations. Example 16. Solving the recurrence relation ak = 3 ak-1 for k=1, 2, 3, … and initial condition a 0 = 2. Sol : 另法: (by 7. 2節Thm 1公式) r – 3 = 0 r = 3 an = a 3 n ∵ a 0 = 2 = a ∴ an = 2 3 n Ch 7 -43

Let generating function for {ak}. First note that ak = 3 ak-1 be the 從k = 1開始,以避免ak-1變成a-1 G(x) - a 0 = 3 x G(x) ∵a 0 = 2 G(x) - 3 x G(x) = G(x)(1 -3 x) = 2 ∴ ak = 2 3 k Exercise : 5, 7, 11, 33 Ch 7 -44

Example 17 Solving ak = 8 ak-1 +10 k-1 for k =1, 2, 3, … and initial condition a 1 = 9. (Sec. 7. 1 Example 7) Sol : Let a 0 = 1 (為計算方便而假設). Let be the generating function for {ak}. Ch 7 -45
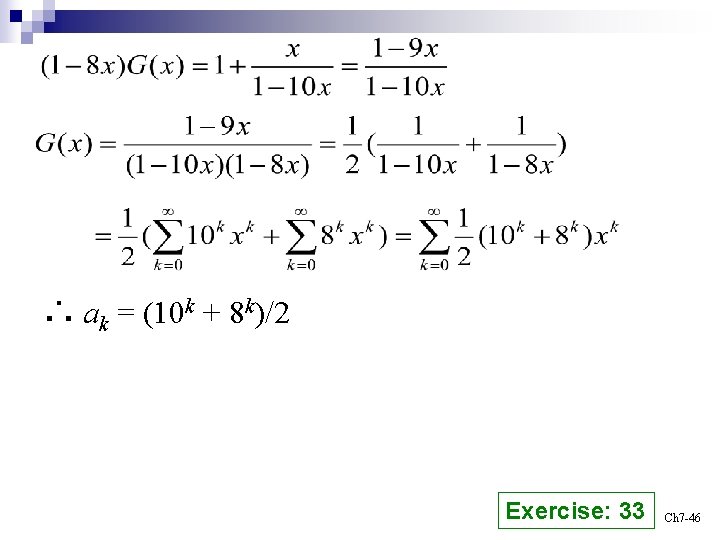
∴ ak = (10 k + 8 k)/2 Exercise: 33 Ch 7 -46

7. 5 Inclusion-Exclusion 排容原理 A, B, C, D : sets A |A|+|B|+|C| 時 各部分被計算的次數 1 2 1 B 1 2 3 1 0 2 1 21 1 C -|A B|-|A C|-|B C|後 +|A B C|後 Ch 7 -47

Theorem 1. A 1, A 2, …, An : sets Exercise : 17 Ch 7 -48

7. 6 Applications of Inclusion and Exclusion Example 1. How many solutions does x 1 + x 2 + x 3 = 11 have, where x 1, x 2, x 3 are nonnegative integers with x 1 3, x 2 4, and x 3 6? Sol : Let a solution have property P 1 if x 1 4, property P 2 if x 2 5, and property P 3 if x 3 7. N(P 1’P 2’P 3’) = N - N(P 1) - N(P 2) - N(P 3) + N(P 1 P 2) + N(P 2 P 3) + N(P 1 P 3) - N(P 1 P 2 P 3) Ch 7 -49

The Number of Onto Functions Example 2. How many onto functions are there form set A={1, 2, 3, 4, 5, 6} to set B={a, b, c} ? Sol : f : A → B f (1)= f (2)= ︰ ︰ f (6)= {a, b, c} 不同的填法造出不同的函數 如何使a, b, c都出現 ? The number of onto functions = (所有函數個數) - (a, b, c中有一個沒被對應) + (a, b, c中二個沒被對應) - (a, b, c都沒被對應) = Ch 7 -50

Thm 1. |A| = m , |B| = n There are onto functions f : A → B. pf : A = {a 1, a 2, …, am}. B = {b 1, b 2, …, bn} f (a 1)= b 1, b 2, …, bn f (a 2)= ︰ f (am)= ︰ Exercise : 8 Ch 7 -51

Example 3. How many ways are there to assign five different jobs to four different employees if every employee is assigned at least one job? Sol : Consider the assignment of jobs as a function from the set of five jobs to the set of four employees. The number of onto functions Exercise : 9 Ch 7 -52

Derangements (亂序) Def. A derangement is a permutation of objects that leaves no object in its original position. Example 5. The permutation 21453 is a derangement of 12345. But 21543 is not a derangement of 12345. Ch 7 -53

Def. Let Dn be the number of derangements of n objects. D 2 = 1 because the derangements of 12 are 21. D 3 = 2 because the derangements of 123 are 231 and 312. D 4 = (所有4個元素的permutation數) - (4個元素有一個在原位置的permutation數) + (4元素中有二個在原位置的permutation個數) - (4個元素中有三個在原位置的permutation個數) + (4元素都在原位置的permutation個數) = Ch 7 -54

Theorem 2. (亂序公式) Proof. Exercise : 13 Ch 7 -55

Exercise 17. How many ways can the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 be arranged so that even digit is in its original position? Sol : Ch 7 -56