Discrete Mathematics Chapter 3 The Fundamentals Algorithms the

Discrete Mathematics Chapter 3 The Fundamentals : Algorithms, the Integers, and Matrices 大葉大學 資訊 程系 黃鈴玲(Lingling Huang)

3. 1 Algorithms Def 1. An algorithm is a finite sequence of precise instructions for performing a computation or for solving a problem. n Example 1. Describe an algorithm for finding the maximum value in a finite sequence of integers. (假設給定的sequence是a 1, a 2, …, an) Ch 3 -2

Solution : ( English language) 1. Set the temporary maximum equal to the first integer in the sequence. 2. Compare the next integer in the sequence to the temporary maximum, and if it is larger than the temporary maximum, set the temporary maximum equal to this integer. 3. Repeat the previous step if there are more integers in the sequence. 4. Stop when there are no integers left in the sequence. The temporary maximum at this point is the largest integer in the sequence. Ch 3 -3

Solution : (pseudo-code) Algorithm 1. Finding the Maximum Element procedure max(a 1, a 2, …, an : integers) max : = a 1 for i : = 2 to n if max < ai then max : = ai { max is the largest element} Ch 3 -4

※ There are several properties that algorithms generally share : n Input n Output n Definiteness : The steps of an algorithm must be defined precisely. n Correctness : produce correct output values n Finiteness : produce the desired output after a finite number of step. n Effectiveness n Generality : The procedure should be applicable for all problems of the desired form, not just for a particular set of input values. Ch 3 -5

※ Searching Algorithms Problem : Locate an element x in a list of distinct elements a 1, a 2, …, an, or determine that it is not in the list. 做法 : linear search, binary search. Algorithm 2. The linear search algorithm procedure linear_search( x : integer, a 1, a 2, …, an: distinct integers) i : = 1 While ( i ≤ n and x≠ai ) i : = i + 1 if i ≤ n then location : = i else location : = 0 { location = j if x = aj; location = 0 if x≠ai, ∀i } Ch 3 -6

Algorithm 3. The Binary Search Algorithm procedure binary_search( x : integer, a 1, a 2, …, an : increasing integers) i : =1 { i is left endpoint of search interval } j : = n { j is right endpoint of search interval } while i < j begin m : = if x > am then i : = m+1 else j : = m end if x = ai then location : = i else location : = 0 { location = i if x = ai , location = 0 if x≠ai , ∀i } Ch 3 -9

※ Sorting Algorithms n n Problem : Suppose that we have a list of elements, a sorting is putting these elements into a list in which the elements are in increasing order. eg. 7, 2, 1, 4, 5, 9 => 1, 2, 4, 5, 7, 9 d, t, c, a, f => a, c, d, f, t 解法有很多，此處僅介紹 : bubble sort (氣泡排序法) ，及 insertion sort (插入排序法)。 Bubble Sort 概念 : 設原 list 為 a 1, …, an。 ¨ 從a 1, a 2開始，向後兩兩比較，若ai > ai+1 則交換，當檢查 完 an 時，an 必定是最大數。 ¨ 再從 a 1, a 2 開始向後比較，若ai > ai+1 則交換，此時只需檢 查到 an-1 即可。 ¨ 依此類推。 Ch 3 -10

n n Example 4. Use the bubble sort to put 3, 2, 4, 1, 5 into increasing order. Sol : First pass (i=1) : 3 2 4 1 5 2 3 4 1 5 Third pass (i=3) : 2 1 3 4 5 1 2 3 4 5 Second pass (i=2) : 2 3 1 4 5 2 1 3 4 5 Fourth pass (i=4) : 1 2 3 4 5 Ch 3 -11

Algorithm 4 The Bubble Sort procedure bubble_sort (a 1, …, an ) for i : = 1 to n-1 for j : = 1 to n-i if aj > aj+1 then interchange aj and aj+1 { a 1, a 2, …, an is in increasing order } Ch 3 -12

Algorithm 5 The Insertion Sort procedure insertion_sort ( a 1, …, an : real numbers with n ≥ 2 ) for j : = 2 to n begin i : = 1 找出 aj 應插入的位置 while aj > ai 最後ai-1 < aj <= ai i : = i + 1 m : = aj for k : = 0 to j – i – 1 將 ai, ai+1, …, aj-1 aj-k : = aj-k-1 全部往右移一格 ai : = m end { a 1, a 2, …, an are sorted } ( Exercise : 3, 9, 13, 23, 35, 39 ) Ch 3 -15

3. 2 The Growth of Functions n n To analyze the practicality of the program, we need to understand how quickly the function (number of operations used by this algorithm) grows as n (number of input elements) grows. eg. sort n objects ¨ Alg. 1 : n 2次計算 ¨ Alg. 2 : 8 n次計算 n # Alg. 1 of Alg. 2 op. 1 1 8 2 4 16 3 9 24 … … … 8 64 64 9 81 72 10 100 80 better! Ch 3 -16

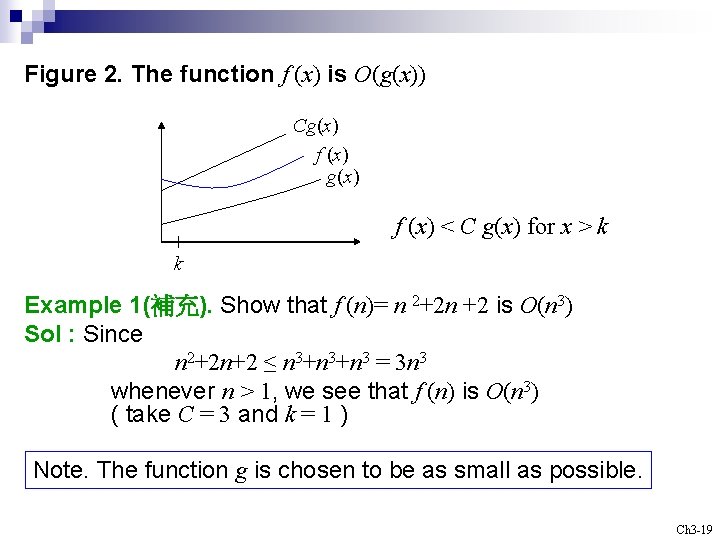
Def 1. ( Big-O notation ) Let f and g be functions from the set of integers to the set of real numbers. We say that f (x) is O(g(x)) if there are constants C and k such that | f (x) | ≤ C | g(x) | whenever x > k. ( read as “f (x) is big-oh of g(x)” ) Ch 3 -17

Example 1. Show that f (x) = x 2+2 x+1 is O(x 2) Sol : Since x 2+2 x+1 ≤ x 2+2 x 2+x 2 = 4 x 2 whenever x > 1 , it follows that f (x) is O(x 2) (take C = 4 and k =1 ) 另法： If x > 2, we see that x 2+2 x+1 ≤ x 2+x 2 = 3 x 2 ( take C = 3 and k = 2 ) Ch 3 -18

Figure 2. The function f (x) is O(g(x)) Cg(x) f (x) < C g(x) for x > k k Example 1(補充). Show that f (n)= n 2+2 n +2 is O(n 3) Sol : Since n 2+2 n+2 ≤ n 3+n 3 = 3 n 3 whenever n > 1, we see that f (n) is O(n 3) ( take C = 3 and k = 1 ) Note. The function g is chosen to be as small as possible. Ch 3 -19

Theorem 1. Let f (x) = anxn+an-1 xn-1+…+a 1 x+a 0 where a 0, a 1, …, an are real numbers. Then f (x) is O(xn). Example 5. How can big-O notation be used to estimate the sum of the first n positive integers? ( i. e. , ) Sol : 1 + 2 + 3 + … + n ≤ n + … + n = n 2 ∴ is O(n 2), taking C =1 and k =1. Ch 3 -20

Example 6. Give big-O estimates for f (n) = n! Sol : n! = 1 2 3 … n ≤ n n … n = nn ∴ n! is O(nn) , taking C =1 and k =1. Example 7. (see Figure 3) 常見function的成長速度由小至大排列： 1 < log n < n 2 < 2 n < n! Theorem 2, 3 Suppose that f 1(x) is O(g 1(x)) and f 2(x) is O(g 2(x)), then (f 1+f 2)(x) is O(max(|g 1(x)|, |g 2(x)|)), (f 1 f 2)(x) is O(g 1(x) g 2(x)). Ch 3 -21

Exercise 7, 11, 19 Exercise 19(c) : f (n) = (n!+2 n)(n 3+log(n 2+1)) (n!+n!)(n 3+n 3) = 4 n 3 n! ∴ f (n) is O(n 3 n!) 取 C = 4, k = 3 Ch 3 -22

3. 3 Complexity of Algorithms Q : How can the efficiency of an algorithm be analyzed ? Ans : (1) time (2) memory Def : ¨ Time complexity : an analysis of the time required to solve a problem of a particular size. (評量方式 : 計算 # of operations，如 “comparison”次數， “加法” 或 “乘法” 次數等) ¨ Space complexity : an analysis of the computer memory required to solve a problem of a particular size. (通常是資 料結構探討的範圍) Ch 3 -23

Example 1. Describe the time complexity of Algorithm 1. Sol : (計算 # of comparisons) Algorithm 1. ( Find Max ) procedure max(a 1, …, an : integers) max : = a 1 for i : = 2 to n if max < ai then max : = ai i 值一開始 = 2 逐次加一，並比較是否>n. 當 i 變成 n+1 時 因比 n 大，故結束 for 迴圈。 ∴ 共有 n 次 comparison { max is the largest element } 共有 n-1 次 comparison 故整個演算法共做 2 n-1 次 comparison 其 time complexity 為 O(n). Ch 3 -24

Example 2. Describe the time complexity of the linear search algorithm. Algorithm 2 ( Linear Search ) procedure ls ( x : integer , a 1, …, an : distinct integers ) i : = 1 Sol : ( 計算 # of comparisons ) While ( i n and x ≠ai ) (Case 1) 當 x = ai for some i n 時 i : = i +1 此行只執行 i 次，故此行共 2 i次比較 if i n then location : = i 加上if，共計 2 i +1次 comparisons. else location : = 0 (Case 2) 當 x ≠ ai for all i 時 location = i x = ai = 0 x ai i 此行執行 n 次後 第 n + 1 次時 i = n + 1 > n 即跳出 ∴共計 2 n+2 次 comparisons 由(1)、(2)取 worst-case 演算法的 time complexity為 O(n) Ch 3 -25

Example 4. Describe the average-case performance of the linear search algorithm, assuming that x is in the list. Alg. 2 ( Linear Search ) procedure ls ( x, a 1, …, an) i : = 1 While ( i n and x ≠ai ) i : = i +1 if i n then location : = i else location : = 0 Sol : ( 計算 “平均比較次數” ) 已知當 x = ai 時，共需 2 i + 1 次比較. ( by Example 2 ) x = a 1, a 2, …, 或 an 的機率都是 1/n. ∴平均比較次數 (即期望值) = ( x = a 1 的比較次數 ) × ( x = a 1 的機率 ) + ( x = a 2 的比較次數 ) × ( x = a 2 的機率 ) +… + ( x = an 的比較次數 ) × ( x = an 的機率 ) = 3 × 1/n + 5 × 1/n + … + ( 2 n+1) × 1/n = ( 3+5+…+(2 n+1)) /n ∴average-case的time complexity為O(n) Ch 3 -26

Example 3. Describe the time complexity of the binary search algorithm. Alg. 3 ( Binary Search ) procedure bs ( x : integer, a 1, …, an : increasing integers ) i : = 1 { left endpoint } j : = n { right endpoint } Sol : 設 n = 2 k 以簡化計算 while i < j /* ( k+1 次) (若 n < 2 k，其比較次數必小於等 begin 於 n = 2 k 的情況) m : = ( i + j ) / 2 因while迴圈每次執行後 if x > am then i : = m+1 /* ( k次 ) 整個 list 會切成兩半 else j : = m 故最多只能切 k 次 end 就會因 i = j 而跳出迴圈 if x = ai then location : = i /* ( 1次 ) ∴共比較 2 k+2 次 else location : = 0 time complexity 為 O(k) = O(log n) Ch 3 -27

Example 5. What is the worst-case complexity of the bubble sort in terms of the number of comparisons made ? Sol : 共 n-1 個 pass procedure bubble_sort ( a 1, …, an ) for i : = 1 to n -1 for j : = 1 to n – i if aj > aj+1 then interchange aj and ai+1 { a 1, …, an is in increasing order } Note 1. 不管何種 case 都需做 第 i 個 pass 需 n – i 次比較 ∴共計 (n-1)+(n-2)+…+1 = 次比較 ∴ O(n 2) 次比較。 Note 2. For 迴圈所需比較次數通常會省略，因此Example 5, 6 不再考慮。 Ch 3 -28

n Example 6. What is the worst-case complexity of the insertion sort in terms of the number of comparisons made ? procedure insertion_sort ( a 1, …, an ) Sol : 做最多次比較的情況如下： for j : = 2 to n 在考慮 aj 時 begin i : = 1 a 1 < a 2 < … < aj-1 < aj 此時共做 j 次比較 while aj > ai i : = i +1 故共計 m : = aj 2+3+…+n = -1 次比較 for k : = 0 to j - i -1 aj-k : = aj-k-1 ai : = m O(n 2) (即 worst case 是 a 1 < a 2 < … < an) end { a 1, …, an are sorted } Ch 3 -29

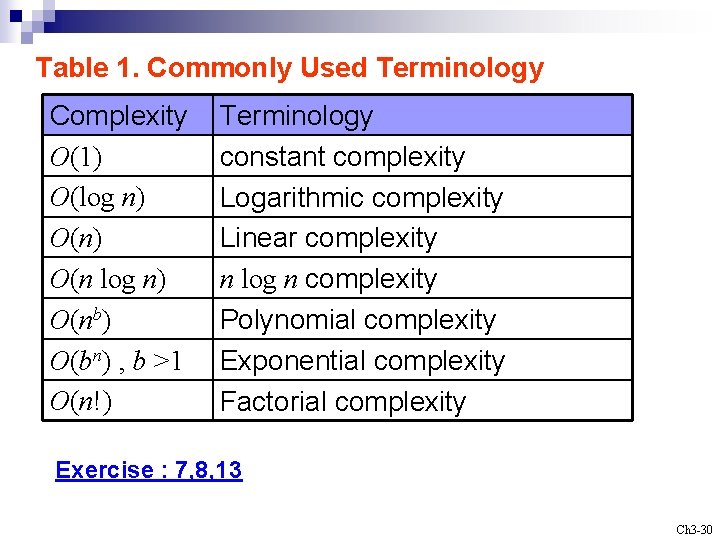
Table 1. Commonly Used Terminology Complexity O(1) O(log n) O(nb) O(bn) , b >1 O(n!) Terminology constant complexity Logarithmic complexity Linear complexity n log n complexity Polynomial complexity Exponential complexity Factorial complexity Exercise : 7, 8, 13 Ch 3 -30

3. 4 The integers and division ※探討一些 Number Theory 的基本觀念 Def 1. a, b : integers, a≠ 0. a divides b (denote a | b) if c Z , b=ac. (a : a factor of b, b : a multiple of a) (a b if a does not divide b) Corollary 1. If a, b, c Z and a | b , a | c. then a | mb+nc whenever m, n Z Def 2. In the quality a = dq + r with 0 r < d, d is called the divisor (除數), a is called the dividend (被除數), q is called the quotient (商數), and r is called the remainder (餘數). q = a div d, r = a mod d Ch 3 -31

Def 3. If a, b Z, m Z+, then a is congruent (同餘) to b modulo m if m | (a-b). (denote a≡b (mod m)). Thm 4. Let m Z+, a, b Z. a≡b (mod m) iff k Z, s. t. a=b+km. Thm 5. Let m Z+, a, b Z. If a≡b (mod m) and c≡d (mod m), then a+c≡b+d (mod m) and ac≡bd (mod m). Ch 3 -32

3. 5 Primes and Greatest Common Divisors Def 1. p Z+ -{1} is called prime (質數) if a p, 1<a< p, a Z+. p is called composite (合成數) otherwise. Thm 1. (The fundamental theorem of arithmetic) Every positive integer greater than 1 can be written uniquely as a prime or as the product of two or more primes where the prime factors are written in order of nondecreasing size. Example 2. The prime factorization (因數分解) of 100 is 2252. Ch 3 -33

Thm 2. If n is a composite integer, then n has a prime divisor less than or equal to. Thm 3. There are infinitely many primes. Pf. 假設質數只有n個：p 1, p 2, …, 及 pn， 令Q = p 1 p 2…pn+1, 因 p 1, …, pn 都不整除Q，得證。 ※目前為止所知最大的質數是 2 p -1的形式, where p is prime. 稱為 Mersenne primes (梅森質數). Example 5. 22 -1=3, 23 -1=7, 25 -1=31 are primes, but 211 -1=2047=23 89 is not a prime. Def 2. gcd ( greatest common divisor ) Def 3. relatively prime (互質) Def 5. lcm ( least common multiple ) Ch 3 -34

Exercise 14. How many zeros are there at the end of 100! ? Sol : 計算 1 2 3 … 100=10 k m, where 10 m ∵ 10=2 5，又2的次數必定比 5多 ∴ 計算 1 2 3 … 100=5 k n, where 5 n ∵ 5, 10, 15, 20, …, 100才有因數 5, 而25, 50, 75, 100有因數 25 ∴ k=24 共有24個0 Homework : 試寫一alg. 求出 n 的所有質數 Ch 3 -35

3. 6 Integers and Algorithms ※The Euclidean Algorithm (輾轉相除法求 gcd ) Example : Find gcd(91, 287) Sol: if x|91 & x|287 x|14 287 = 91 3 + 14 ∴gcd (91, 287) = gcd(91, 14) gcd (91, 14) = gcd (14, 7) 91 = 14 6 + 7 gcd (14, 7) = 7 14 = 7 2 ∴ gcd(91, 287) = 7 Lemma 1 Let a = bq + r, where a, b, q, and r Z. Then gcd(a, b) = gcd (b, r). Ch 3 -36

Algorithm 6. ( The Euclidean Algorithm) procedure gcd ( a, b : positive integers) x : = a y : = b while y≠ 0 begin r : = x mod y ( if y > x then r = x) x : = y y : = r end { gcd (a, b) = x } Exercise : 23, 25 eg. 求 gcd (6, 12) x=6 y = 12 while y≠ 0 r = 6 mod 12 =6 x = 12 y=6 while y≠ 0 r = 12 mod 6 = 0 x=6 y=0 while y = 0 , end. ∴ gcd (6, 12) = 6 Ch 3 -37

3. 7 Applications of Number Theory gcd(a, b) can be expressed as a linear combination with integer coefficients of a and b. Theorem 1. If a and b are positive integers, then there exist integers s and t such that gcd(a, b) = sa+tb. ※將gcd(a, b) 寫成a 跟 b的線性組合： The extended Euclidean Algorithm Ch 3 -38

Example 1 Express gcd(252, 198) =18 as a linear combination of 252 and 198. Sol: 252 = 1 198 + 54 198 = 3 54 + 36 54 = 1 36 + 18 18 = 54 – 1 36 36 = 2 18 36 =198 – 3 54 ∴ gcd(252, 198) = 18 54 =252 – 1 198 18 = 54 – 1 36 = 54 – 1 (198 – 3 54 ) = 4 54 – 1 198 = 4 (252 – 1 198) – 1 198 = 4 252 – 5 198 Exercise : 1(g) Ch 3 -39

Lemma 1. If a, b and c are positive integers such that gcd(a, b) = 1 and a | bc, then a | c. Lemma 2. If p is a prime and p | a 1 a 2…an, where each ai is an integer, then p | ai for some i. Example 2 14 8 (mod 6), 但 的左右兩邊同除以 2後不成立 because 14/2=7, 8/2=4, but 7 4(mod 6). 另, 14 8 (mod 3), 同除以 2後, 7 4 (mod 3)成立 Q: 何時可以讓 的左右同除以一數後還成立呢？ Ch 3 -40

Theorem 2. Let m be a positive integer and let a, b, and c be integers. If ac bc (mod m) and gcd(c, m) = 1, then a b (mod m). ※ Linear Congruences A congruence (同餘式) of the form ax b (mod m), where m is a positive integer, a and b are integers, and x is a variable, is called a linear congruence. How can we solve the linear congruence ax b (mod m)? Def: If ax 1 (mod m), and let a be an answer of x, a is called an inverse (反元素) of a modulo m Ch 3 -41

Theorem 3. If a and m are relatively prime integers and m>1, then an inverse of a modulo m exists. Furthermore, this inverse is unique modulo m. Proof. (existence) (unique的部分是exercise) By Thm 1, because gcd(a, m) = 1, there exist integers s and t such that sa + tm =1. sa + tm 1 (mod m). Because tm 0 (mod m), sa 1 (mod m), s is an inverse of a modulo m. Ch 3 -42

Example 3 Find an inverse of 3 modulo 7. Sol. Because gcd(3, 7) = 1, find s, t such that 3 s + 7 t =1. 7=2 3+1 1 = -2 3 + 1 7 -2 is an inverse of 3 modulo 7. (Note that every integer congruent to -2 modulo 7 is also an inverse of 3, such as 5, -9, 12, and so on. ) Exercise : 5 Ch 3 -43

Example 4 What are the solutions of the linear congruence 3 x 4 (mod 7)? Sol. By Example 3 -2 is an inverse of 3 modulo 7 3 (-2) 1 (mod 7) 將 3 x 4 (mod 7) 左右同乘 -2 3 x -2 4 (mod 7) -6 x -8 (mod 7) Because -6 1 (mod 7), and -8 6 (mod 7), If x is a solution, then x -8 6 (mod 7). We need to determine whether every x with x 6 (mod 7) is a solution. Assume x 6 (mod 7), then 3 x 3 6 = 18 4 (mod 7). Therefore every such x is a solution: x = 6, 13, 20, …, and -1, -8, -15, …. Exercise : 11 Ch 3 -44

The Chinese Remainder Theorem (中國餘數定理) Example 5. 孫子算經 : 「某物不知其數，三三數之餘二，五五數之 餘三，七七數之餘二，問物幾何 ? 」 (又稱為「韓信點兵」問題) i. e. x ≡ 2 (mod 3) x ≡ 3 (mod 5) x=? x ≡ 2 (mod 7) Theorem 4. (The Chinese Remainder Theorem) Let m 1, m 2, …, mn be pairwise relatively prime positive integers and a 1, a 2, …, an arbitrary integers. Then the system x ≡ a 1 (mod m 1) x ≡ a 2 (mod m 2) : x ≡ an (mod mn) has a unique solution modulo m = m 1 m 2…mn. (即有一解 x, where 0 x < m , 且所有其他解 mod m都等於 x) Ch 3 -45

x ≡ a 1 (mod m 1) x ≡ a 2 (mod m 2) : x ≡ an (mod mn) m = m 1 m 2…mn Proof of Thm 4: Let Mk = m / mk 1 k n ∵ m 1, m 2, …, mn are pairwise relatively prime ∴ gcd (Mk , mk) = 1 integer yk s. t. Mk yk ≡ 1 (mod mk) ( by Thm. 3) ak Mk yk ≡ ak (mod mk) , 1 k n Let x = a 1 M 1 y 1+a 2 M 2 y 2+…+an Mn yn ∵ mi | Mj , i ≠ j ∴ x ≡ ak Mk yk ≡ ak (mod mk) 1 k n x is a solution. All other solution y satisfies y ≡ x (mod mk). Ch 3 -46

Example 6. (Solve the system in Example 5) Let m = m 1 m 2 m 3 = 3 5 7 = 105 M 1 = m / m 1 = 105 / 3 = 35 (也就是m 2 m 3) M 2 = m / m 2 = 105 / 5 = 21 M 3 = m / m 3 = 105 / 7 = 15 x ≡ 2 (mod 3) x ≡ 3 (mod 5) x ≡ 2 (mod 7) x=? 找 y 1 使得M 1 y 1 = 1 (mod M 1 y 1 3) 35 ≡ 2 (mod 3) 35 2 ≡ 2 2 ≡ 1 (mod 3) 21 ≡ 1 (mod 5) 15 ≡ 1 (mod 7) M 2 y 2 M 3 y 3 21 1 ≡ 1 (mod 5) 15 1 ≡ 1 (mod 7) ∴ x = a 1 M 1 y 1 + a 2 M 2 y 2 + a 3 M 3 y 3 = 2 35 2 + 3 21 1 + 2 15 1 = 233 ≡ 23 (mod 105) ∴ 最小的解為 23，其餘解都等於 23+105 t for some t Z+ Ch 3 -47

Exercise 18. Find all solutions to the system of congruences x ≡ 2 (mod 3) x ≡ 1 (mod 4) x ≡ 3 (mod 5) Sol : a 1=2 , a 2=1 , a 3=3, m 1=3 , m 2=4 , m 3=5 m=3 4 5=60 M 1=20 , M 2=15 , M 3=12 20≡ 2 (mod 3) 20 2≡ 1 (mod 3) 15≡ 3 (mod 4) 15 3≡ 1 (mod 4) 12≡ 2 (mod 5) 12 3≡ 1 (mod 5) ∴ x = 2 20 2+1 15 3+3 12 3 = 80+45+108=233≡ 53 (mod 60) Ch 3 -48

※ 補充：(when mi is not prime) Ex 20. Find all solutions, if any, to the system of congruences. x≡ 5 (mod 6) x≡ 3 (mod 10) x≡ 8 (mod 15) Sol. Rewrite the system as the following: x ≡ 1 (mod 2) x≡ 2 (mod 3) x ≡ 1 (mod 2) x≡ 3 (mod 5) x ≡ 2 (mod 3) x≡ 3 (mod 5) i. e. , x≡ 1 (mod 2) x≡ 2 (mod 3) … x≡ 3 (mod 5) Exercise : 做完此題 Ch 3 -49

※ 補充：(when mi is a prime power) Ex 21. Find all solutions, if any, to the system of congruences. x≡ 7 (mod 9) x≡ 4 (mod 12) x≡ 16 (mod 21) Sol. Rewrite the system as the following: x≡ 7 (mod 9) (不能拆！) x≡ 0 (mod 4) x≡ 1 (mod 3) x≡ 2 (mod 7) x≡ 1 (mod 3) i. e. , x≡ 7 (mod 9) (此式取代 x≡ 1 (mod 3) 式子) x≡ 0 (mod 4) … x≡ 2 (mod 7) Ch 3 -50

Computer Arithmetic with Large Integers Suppose that m 1, m 2, …, mn be pairwise relatively prime integers greater than or equal to 2 and let m = m 1 m 2 …mn. By the Chinese Remainder Theorem, we can show that an integer a with 0 a < m can be uniquely represented by the n-tuple (a mod m 1, a mod m 2, …, a mod mn). Example 7 What are the pairs used to represent the nonnegative integers x<12 when they are represented by the order pair (x mod 3, x mod 4)? Sol 0=(0, 0), 6=(0, 2), 1=(1, 1), 2=(2, 2), 3=(0, 3), 4=(1, 0), 5=(2, 1), 7=(1, 3), 8=(2, 0), 9=(0, 1), 10=(1, 2), 11=(2, 3). Exercise : 37 Ch 3 -51

To perform arithmetic with larger integers, we select moduli (modulus的複數) m 1, m 2, …, mn, where each mi is an integer greater than 2, gcd(mi, mj)=1 whenever i j, and m=m 1 m 2…mn is greater than the result of the arithmetic operations we want to carry out. Ch 3 -52

Example 8 Suppose that performing arithmetic with integers less than 100 on a certain processor is much quicker than doing arithmetic with larger integers. We can restrict almost all our computations to integers less than 100 if we represent integers using their remainders modulo pairwise relatively prime integers less than 100. For example, 99, 98, 97, and 95 are pairwise relatively prime. every nonnegative integer less than 99 98 97 95 = 89403930 can be represented uniquely by its remainders when divided by these four moduli. E. g. , 123684 = (33, 8, 9, 89), and 413456 = (32, 92, 42, 16) 123684 + 413456 = (33, 8, 9, 89) + (32, 92, 42, 16) = (65 mod 99, 100 mod 98, 51 mod 97, 105 mod 95) = (65, 2, 51, 10) Use Chinese Remainder Thm to find this sum 537140. Ch 3 -53

Theorem 5 (Fermat’s Little Theorem) If p is prime and a is an integer not divisible by p, then a p-1 1 (mod p) Furthermore, for every integer a we have a p a (mod p) Exercise 27(a) Show that 2340 1 (mod 11) by Fermat’s Little Theorem and noting that 2340 = (210)34. Proof 11 is prime and 2 is an integer not divisible by 11. 210 1 (mod 11) 2340 1 (mod 11) by Thm 5 of Sec. 3. 4 (a b (mod m) and c d (mod m) ac bd (mod m) ) Exercise : Compute 52003 (mod 7) Ch 3 -54