Discrete mathematics Discrete i e no continuous Set



































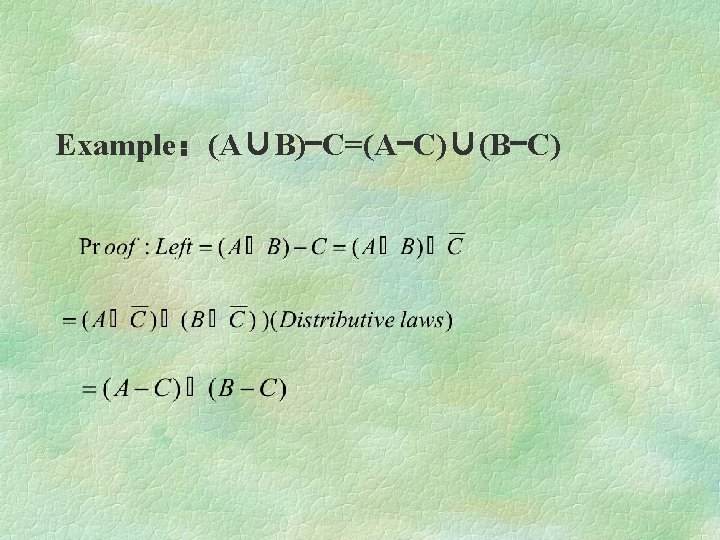

- Slides: 38

§ Discrete mathematics § Discrete i. e. no continuous § Set theory, Combinatorics, Graphs, Modern Algebra(Abstract algebra, Algebraic structures), Logic, classic probability, number theory, Automata and Formal Languages, Computability and decidability etc.

§ § § § § Before the 18 th century, Discrete, quantity and space astronomy, physics Example: planetary orbital, Newton's Laws in Three Dimensions continuous mathematics: calculus, Equations of Mathematical Physics, Functions of Real Variable, Functions complex Variable § Discrete ? stagnancy of

§ § § § in the thirties of the twentieth century, Turing Machines Finite Discrete Data Structures and Algorithm Design Database Compilers Design and Analysis of Algorithms Computer Networks Software information security and cryptography theory of computation New generation computers

§ § § § Set theory, Introductory Combinatorics, Graphs, Algebtaic structures, Logic. This term: Set theory, Introductory Combinatorics , Graphs, Algebtaic structures(Group, Ring,Field). Next term: Algebtaic structures(Lattices and Boolean Algebras), Logic



ⅠIntroduction to Set Theory § The objects of study of Set Theory are sets. As sets are fundamental objects that can be used to define all other concepts in mathematics. § Georg Cantor(1845 --1918) is a German mathematician. § Cantor's 1874 paper, "On a Characteristic Property of All Real Algebraic Numbers", marks the birth of set theory. § paradox

§ § § twentieth century axiomatic set theory naive set theory Concept Relation, function, cardinal number paradox

Chapter 1 Basic Concepts of Sets 1. 1 Sets and Subsets § § What are Sets? A collection of different objects is called a set S, A The individual objects in this collection are called the elements of the set § We write “t A” to say that t is an element of A, and We write “t A” to say that t is not an element of A

§ Example: The set of all integers, Z. § Then 3 Z, -8 Z, 6. 5 Z § These sets, each denoted using a boldface letter, play an important role in discrete mathematics: § N={0, 1, 2, …}, the set of natural number § I=Z={…, -2, -1, 0, 1, 2, …}, the set of integers § I+=Z+={1, 2, …}, the set of positive integers § I-=Z-={-1, -2, …}, the set of negative integers § Q={p/q|p Z, q 0}, the set of rational numbers § Q+, the set of positive rational numbers § Q-, the set of negative rational numbers

§ 1. Representation of set § (1)Listing elements, One way is to list all the elements of a set when this is possible. . § Example: The set A of odd positive integers less than 10 can be expressed by A={1, 3, 5, 7, 9}。 § B={x 1, x 2, x 3} √

§ (2)Set builder notion: We characterize the property or properties that the elements of the set have in common. § Example: The set A of odd positive integers less than 10 can be expressed by A={x|x is an odd positive integer less than 10} § Example: C={x|x=y 3, y Z+} § C describes the set of all cubes of positive integers. § D={x|-1<x<2}

§ (3)Recursive definition § Recursive definitions of sets have three steps: § 1)Basic step: Specify some of the basic elements in the set. § 2)recursive step: Give some rules for how to construct more elements in the set from the elements that we know are already there. § 3) closed step: There are no other elements in the set except those constructed using steps 1 and 2.

§ Example: The set of even nonnegative integers E’={x|x≧ 0, and x=2 y, where y Z} § (1)Basic step: 0 E+。 § (2)Recursive step: If n E+, then n+2 E+. § (3)Closed step: There are no other elements in the set E’ except those constructed using steps (1) and (2). § Example: § (1)Basic step: 3 S。 § (2)Recursive step: If x and y S, then x+y S。 § (3)Closed step: There are no other elements in the set S except those constructed using steps (1) and (2). § S=? § S={y|y=3 x, x Z+}

§ Let ai Σ, sequences of the form a 1 a 2…an are often in computer science. These finite sequences are also called strings. The length of the string S is the number of terms in this string. § The empty string, denoted by , is the string that has no terms. The empty string has length zero. § If x=a 1 a 2…an, and y=b 1 b 2…bm are strings, where ai, bj Σ(1≦i≦n, 1≦j≦m), we define the catenation of x and y as the string a 1 a 2…an b 1 b 2…bm. § The catenation of x and y is written as xy, and is another string from Σ, i. e. xy=a 1 a 2…an b 1 b 2…bm. § Note x =x and x=x.

§ Let Σ be an alphabet, we can construct the set Σ+ consisting of all finite nonempty string of elements of Σ: § (1)Basic step: If a Σ, then a Σ+. § (2)Recursive step: If a and x Σ+, then ax Σ+. § (3)Closed step: There are no other elements in the set Σ+ except those constructed using steps (1) and (2). § Σ+ element or string: infinite § Length of string: finite, 1, 2, 3, …

§ Let Σ be an alphabet, we can construct the set Σ* consisting of all finite string of elements of Σ: § (1)Basic step: Σ*. § (2)Recursive step: If x Σ* and a Σ then xa Σ*. § (3)Closed step: There are no other elements in the set Σ* except those constructed using steps (1) and (2).

§ Arithmetic expressions § (B) A numeral is an arithmetic expression. § (R) If e 1 and e 2 are arithmetic expressions, then § all of the following are arithmetic expressions: § e 1+e 2, e 1−e 2, e 1*e 2, e 1/e 2, (e 1) § (C)There are no other arithmetic expressions except those constructed using steps (1) and (2).

§ A={1, 3, 5, 7, 9}, B={x 1, x 2, x 3}, finite elements, § 5 3 § C={x|x=y 3, y Z+}, infinite elements § A set S is called finite set if it has n distinct elements, where n N. In this case, n is called the cardinality of S and is denoted by |S|. A set that is not finite is called infinite set. § Σ*, Σ+, C, D, S are infinite sets, A, B are finite sets. § P={x|x is an prime number less than 6}, 2, 3, 5, |P|=3

§ Example: A={x|x 2+1=0, and x is an real number}, § No element § empty set, |A|=0. § The set that has no elements in it is denoted by {} or the symbol and is called the empty set. § Note: { } is not an empty set. It is a set with one element which the element is the empty set. § { }, but . § universal set § The universal set is the set of all elements under consideration in a given discussion. We denote the universal set by U.

§ (1)The order in which the elements of a set are listed is not important. § {a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, and {c, b, a} are all representations of the same set. § (2) In the listing of the elements of a set, repeated elements aren't allowed. § (3)A set can be an element of another set § Example: S={{a, b}, {a, b, c}, {d, e}} § Note: {a, b, c} is also a set consisting of elements a, b, c。a, b, and c aren’t elements of S.

§ Example: Let S={ , { }}。 Elements of S are and { }

§ 2. Subsets § Definition 1. 1: Let A and B are two sets. If every element of A is also an element of B, that is, if whenever x A then x B, we say that A is a subset of B or that A is contained in B, and we write A B。 If there is an element of A that is not in B, then A is not a subset of B, and we write A⋢B.

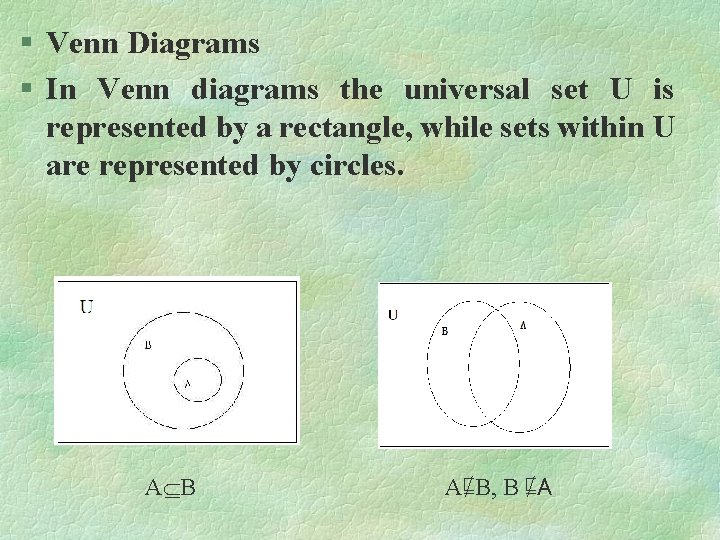
§ Venn Diagrams § In Venn diagrams the universal set U is represented by a rectangle, while sets within U are represented by circles. A B A⋢B, B ⋢A

§ Example: A={x|-1<x<2}. 0. 5 A, but 0. 5 is not an integer, so A={x|-1<x<2}⋢Z, § Z Q, § (1)For any set A, A. § (2)If A B, and B C, then A C

§ Definition 1. 2: Let A and B be sets. We say that A equals B, written A=B, whenever for any x, x A if only if x B. If A and B are not equal, we write A B. § It is easy to see that A=B if only if A B and B A § Definition 1. 3: If A B and A B, we write A B and say that A is a proper subset of B.

§ Example: {a} {a, b}。 § Example: S 1={a}, S 2={{a}}, S 3={a, {a}} § a S 3, S 1 S 3 § {a} S 3, S 2 S 3, § S 1 S 3, S 1 S 2,

§ Theorem 1. 1: For any set A, § (1) A , (2)A A § A={1, 2, 3}, , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}and {1, 2, 3} are subsets of A § power set of A § Definition 1. 4: Given a set A, the power set of A is the set of all subsets of the set A. The power set of A is denoted by P(A). § |A|=k,|P (A)|=? § Theorem 1. 2: If A is a finite set, then |P (A)|=2|A|.

1. 2 Operations on Sets § 1. Definition of operations on sets § Definition 1. 5:Let A and B be two subsets of universal set U, § (1)The union of A and B, write A∪B, is the set of all elements that are in A or B. i. e. A∪B={x|x A or x B}

§ (2)The intersection of A and B, write A∩B, is the set of all elements that are in both A and B. i. e. A∩B= {x|x A and x B}。 (3) The difference of A and B, write A-B, is the set of all elements that are in A but are not in B. i. e. A-B={x|x A and x B}。

The complement of A , write , =U-A, is the set of all elements of U that are not elements of A § Example: A={1, 2, 3, 4, 5}, B={1, 2, 4, 6}, C={7, 8}, U={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}。 A∪B={1, 2, 3, 4, 5, 6}, A∩B={1, 2, 4}, A∩C= , A-B={3, 5}, A-C=A

§ Definition 1. 6: Let A 1, A 2, …An be sets. If I={1, 2, …n}, then § (1)The union of the sets A 1, A 2, …An, A 1∪A 2∪…∪An={x|there is an i I such that x Ai}. § (2)The intersection of the sets A 1, A 2, …An, A 1∩A 2∩…∩An={x|x Ai for all i I}.

§ 2. Properties of set operations § Theorem 1. 3: The operations defined on sets satisfy the following properties: § (1)commutative laws : A∪B=B∪A; A∩B=B∩A § (2)associative laws: A∪(B∪C)=(A∪B)∪C; § A∩(B∩C)=(A∩B)∩C § (3)distributive laws: § A∪(B∩C)=(A∪B)∩(A∪C) § A∩(B∪C)=(A∩B)∪(A∩C) § (4)idempotent laws: A∪A=A; A∩A=A § (5)domination laws A∪U=U; A∩ = § (6)identical laws: A∪ =A; A∩U=A



§ Example:Let A and B be two sets. Then P(A)∩P(B)=P(A∩B) § Proof: (1)P (A)∩P (B) P (A∩B) For any X P(A)∩P(B) (2)P (A∩B) P (A)∩P (B) For any X P(A∩B)
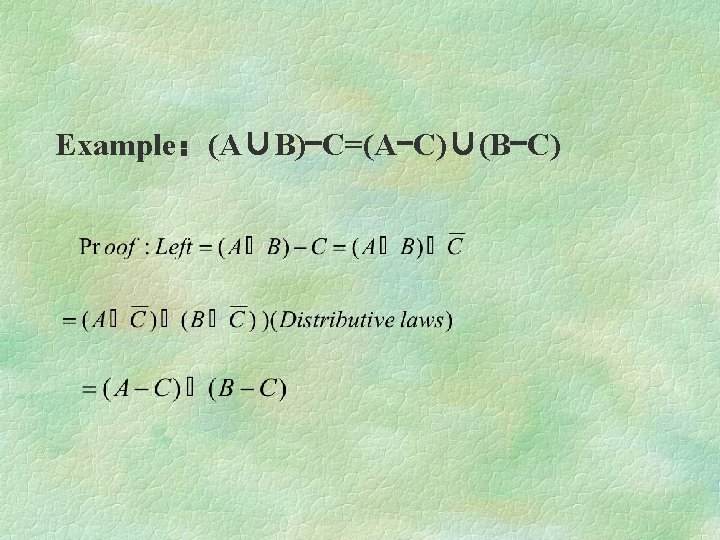
Example:(A∪B)-C=(A-C)∪(B-C)

§ Exercise: P 11 2, 4, 8, 12, 34, 39, 40
 Set identities
Set identities Laws of set theory in discrete mathematics
Laws of set theory in discrete mathematics Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
Training set validation set test set Discrete data
Discrete data What is binary relation
What is binary relation Working memory graphs
Working memory graphs Subtraction rule discrete math
Subtraction rule discrete math Converse of a relation
Converse of a relation Boolean functions in discrete mathematics
Boolean functions in discrete mathematics Proposition math
Proposition math Pigeonhole principle in discrete mathematics
Pigeonhole principle in discrete mathematics Induction and recursion discrete mathematics
Induction and recursion discrete mathematics Recurrence relation in discrete mathematics
Recurrence relation in discrete mathematics Binary relations discrete math
Binary relations discrete math Declarative statement in discrete mathematics
Declarative statement in discrete mathematics Contoh soal relasi matematika diskrit
Contoh soal relasi matematika diskrit Double implication
Double implication Discrete mathematics
Discrete mathematics Discrete mathematics chapter 1
Discrete mathematics chapter 1 Discrete math
Discrete math Dijkstra algorithm discrete mathematics
Dijkstra algorithm discrete mathematics Implication math examples
Implication math examples What is rooted tree in discrete mathematics
What is rooted tree in discrete mathematics Travelling salesman problem discrete mathematics
Travelling salesman problem discrete mathematics Propositional logic puzzles
Propositional logic puzzles Advanced counting techniques in discrete mathematics
Advanced counting techniques in discrete mathematics Floyd warshall algorithm path reconstruction
Floyd warshall algorithm path reconstruction Discrete structures
Discrete structures Prove by exhaustion
Prove by exhaustion Ming-hsuan yang
Ming-hsuan yang Discrete numeric function
Discrete numeric function M ary tree in discrete mathematics
M ary tree in discrete mathematics Law of duality in discrete mathematics
Law of duality in discrete mathematics Eular graph
Eular graph Discrete mathematics
Discrete mathematics Susanna s epp
Susanna s epp Notation for sequences
Notation for sequences Inverse relations
Inverse relations