Discrete Mathematics Chapter 1 The Foundations Logic and

Discrete Mathematics Chapter 1 The Foundations : Logic and Proofs 大葉大學 資訊 程系 黃鈴玲

1 -1 Propositional Logic 命題邏輯 n n n Def : A proposition (命題) is a declarative (敘述) sentence that is either true or false, but not both. Example 1 : (1) Toronto is the capital of Canada. (2) 1 + 1 = 2 都是命題！但(1)是錯誤的命題 Example 2 : (1) What time is it ? (2) Read this carefully. (3) x + 1 = 2 都不是命題！但(3)若給了x的範圍，則可算是命題 Ch 1 -2

Logical operators (邏輯運算子) and truth table (真值表) Def : A truth table (真值表) displays the relationships between the truth values of propositions. (列舉命題所有真假的可能性) n Table 1. The truth table for the Negation (not) (非) of a Proposition eg. p : “Today is Friday. ” ﹁p p ﹁p : “Today is not Friday. ” F T Ch 1 -4

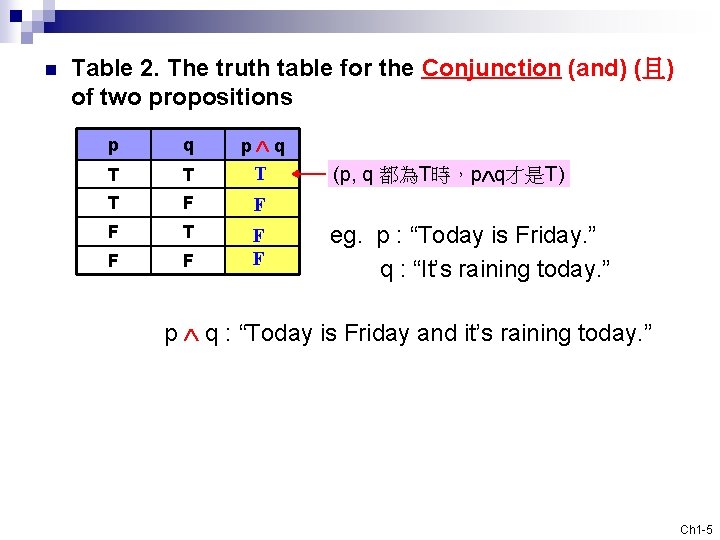
n Table 2. The truth table for the Conjunction (and) (且) of two propositions p q T T F F F T F F (p, q 都為T時，p q才是T) eg. p : “Today is Friday. ” q : “It’s raining today. ” p q : “Today is Friday and it’s raining today. ” Ch 1 -5

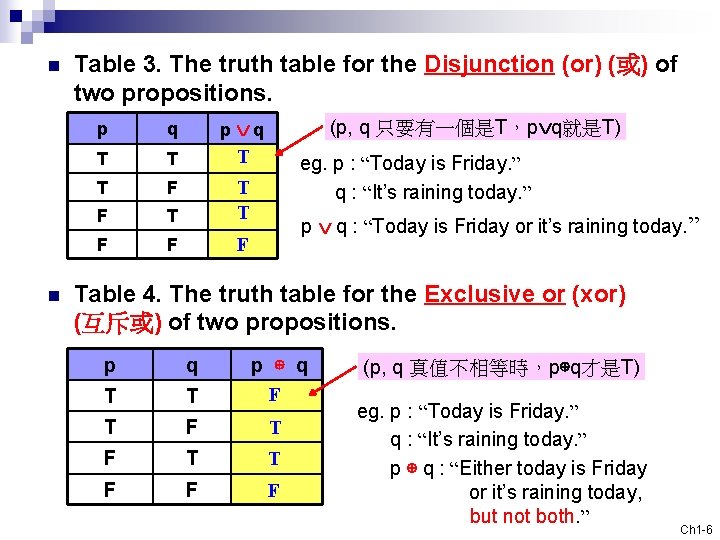
n n Table 3. The truth table for the Disjunction (or) (或) of two propositions. p q T T F F T T T F F F (p, q 只要有一個是T，p q就是T) eg. p : “Today is Friday. ” q : “It’s raining today. ” p q : “Today is Friday or it’s raining today. ” Table 4. The truth table for the Exclusive or (xor) (互斥或) of two propositions. p q T T p ⊕ q F T F T T F F F (p, q 真值不相等時，p⊕q才是T) eg. p : “Today is Friday. ” q : “It’s raining today. ” p ⊕ q : “Either today is Friday or it’s raining today, but not both. ” Ch 1 -6

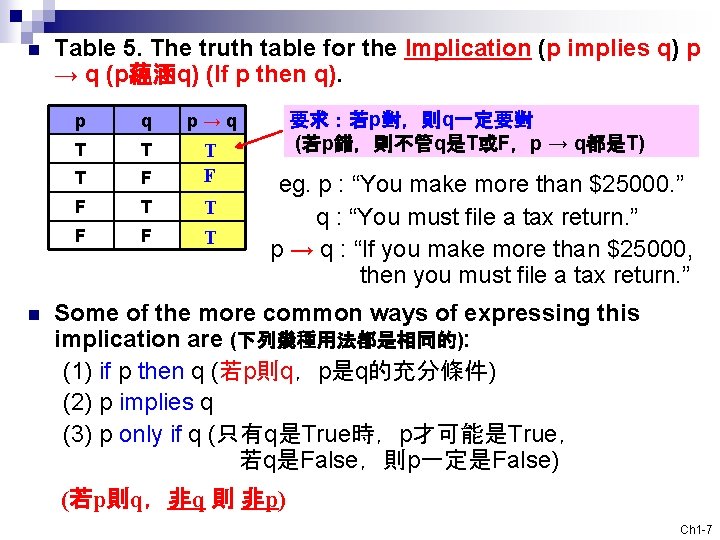
n n Table 5. The truth table for the Implication (p implies q) p → q (p蘊涵q) (If p then q). p q p→q T T T F F T 要求：若p對，則q一定要對 (若p錯，則不管q是T或F，p → q都是T) eg. p : “You make more than $25000. ” q : “You must file a tax return. ” p → q : “If you make more than $25000, then you must file a tax return. ” Some of the more common ways of expressing this implication are (下列幾種用法都是相同的): (1) if p then q (若p則q，p是q的充分條件) (2) p implies q (3) p only if q (只有q是True時，p才可能是True， 若q是False，則p一定是False) (若p則q，非q 則 非p) Ch 1 -7

Def : In the implication p → q , p is called the hypothesis (假設) and q is called the conclusion (結論 ). n Def : Compound propositions (合成命題) are formed from existing propositions using logical operators. (即 、 、 ⊕、 →等) n Table 6. The truth table for the Biconditional p ↔ q (雙蘊涵) ( p → q and q → p ) (p與q的真�相等時才會是 T) p q p→q q→p p↔q T T T (p若且唯若q) F F T T F F “p if and only if q” F T n F F T T T and 運算 “p iff q ” “If p then q , and conversely. ” Ch 1 -8

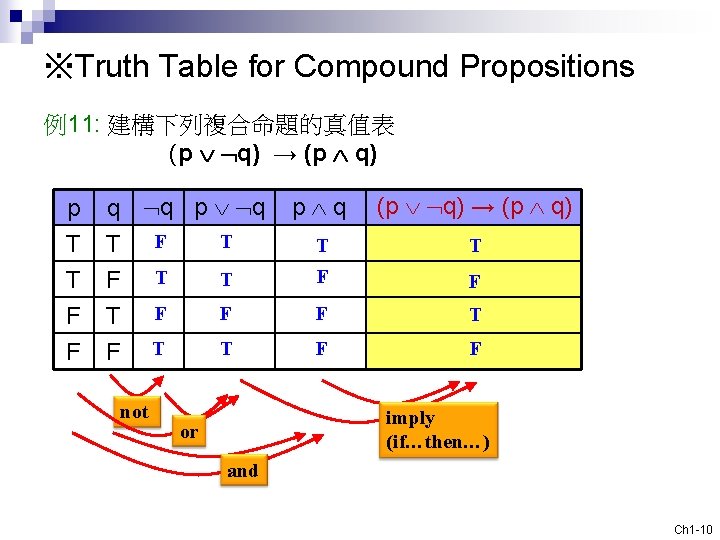
※Truth Table for Compound Propositions 例11: 建構下列複合命題的真值表 (p q) → (p q) p T T F q q p q T T F T F F F not T T p q (p q) → (p q) T T F F F T F F imply (if…then…) or and Ch 1 -10

n Table 8. Precedence of Logical Operators (邏輯運算的優先順序) Operator Precedence ﹁ 1 2 3 → 4 5 eg. (1) p q r means ( p q ) r (2) p q → r means ( p q ) → r (3) p ﹁ q means p ( ﹁ q ) Ch 1 -12

Translating (轉換) English Sentences into Logical Expression Example 12 : How can the following English sentence be translated into a logical expression ? “You can access the Internet from campus only if you are a computer science major or you are not a freshman. ” Sol : a : “You can access the Internet from campus. ” c : “You are a computer science major. ” f : “You are a freshman. ” ∴ a only if ( c or ( ﹁ f )) 即 a → ( c ( ﹁ f )) Ch 1 -13

Def: A set of propositional expressions is consistent (一致) if there is an assignment of truth values to the variables in the expressions that makes each expression true. (一組由數個命題p, q, r等合成的命題， 如：p q, q r, p r 若存在一組真值的給法， 如設 p T, q F, 就像聯立方程式， 存在一組解 r T 使所有的命題都可以為真，即稱為consistent) Ch 1 -16

(等價命題) 1 -2 Propositional Equivalences n n Def 1: A compound proposition that is always true is called a tautology. (真理) A compound proposition that is always false is called a contradiction. (矛盾) Example 1 : p ﹁p p ﹁p T F F T T F always true always false p ﹁p is a tautology. p ﹁p is a contradiction. Ch 1 -20

Def 2: The propositions p and q that have the same truth values in all possible cases are called logically equivalent (等價). (p與q在所有情況的真值都相等) The notation p q ( or p q ) denotes that p and q are logically equivalent. Ch 1 -22

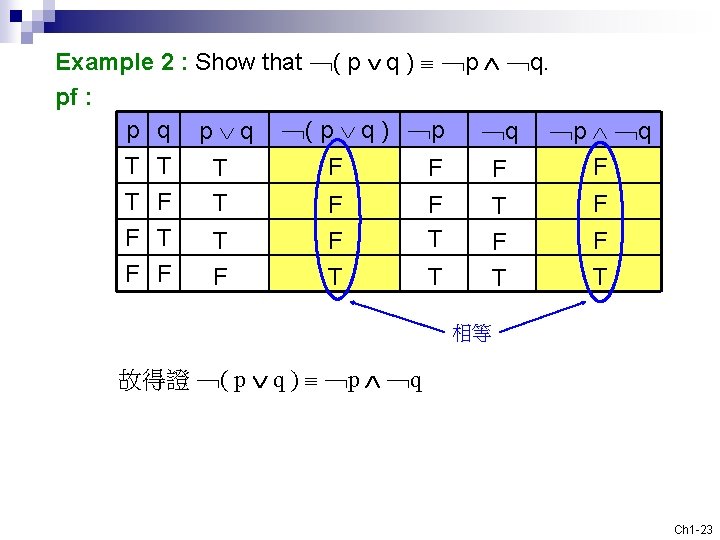
Example 2 : Show that ﹁( p q ) ﹁p ﹁q. pf : p q p q ﹁( p q ) ﹁p ﹁q ﹁p ﹁q T T F F F T T F F F T T 相等 故得證 ﹁( p q ) ﹁p ﹁q Ch 1 -23

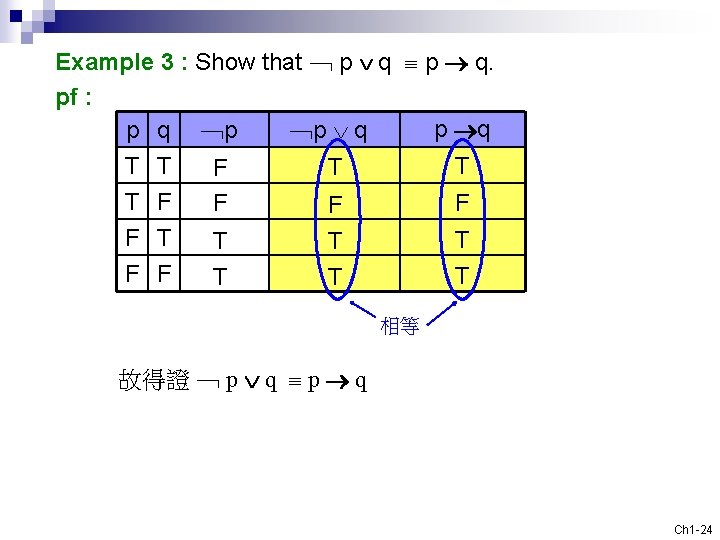
Example 3 : Show that ﹁ p q. pf : p q ﹁p q p q ﹁p T T F T F F F T T T 相等 故得證 ﹁ p q Ch 1 -24

Example 4 : Show that p (q r) (p q) (p r). pf : p q r T T F p (q r) p q p r (p q) (p r) T T T T T F F T T T T F T F T T F F F F F 相等 故得證 p (q r) (p q) (p r) Ch 1 -26

n ※ Some important logically equivalences (表 6, 表 7) (1) p q q p commutative laws. 交換律 (2) p q q p (3) ( p q ) r p (q r ) associative laws. 結合律 (4) ( p q ) r p (q r ) (5) p ( q r ) ( p q ) ( p r ) distributive laws 分配律 (6) p ( q r ) ( p q ) ( p r ) (7) ﹁( p q ) ﹁p ﹁q De Morgan’s laws 笛摩根定律 (8) ﹁( p q ) ﹁p ﹁q (9) p ﹁p T (10) p ﹁p F (11) p → q ﹁p q (例3) ((5)、(6)的觀念類似於c (a + b) = (c a) + (c b) Ch 1 -27

Example 8 : Show ( p q ) → (p q) is a tautology. pf : ( p q ) → (p q) ≡ ﹁( p q ) (p q ) ≡ ( ﹁p ﹁q ) (p q ) ≡ ( ﹁p p ) ( ﹁q q ) ≡T T ≡T By (11) By (7) By (3) Ch 1 -29

1 -3 Predicates and Quantifiers 屬性 n n n 數量詞 目標 : 了解 ∀ 及 ∃ 符號 Def : The statement P(x) is said to be the value of the propositional function P at x. (函數式命題，包含變數) ex : P(x) : “ x 變數 is greater than 3 ” (P(x): x > 3) predicate(屬性) Example 1: 若P(x)代表 “x > 3”，請問P(2)及P(4)的真值為何？ Sol: P(2) F P(4) T Ch 1 -31

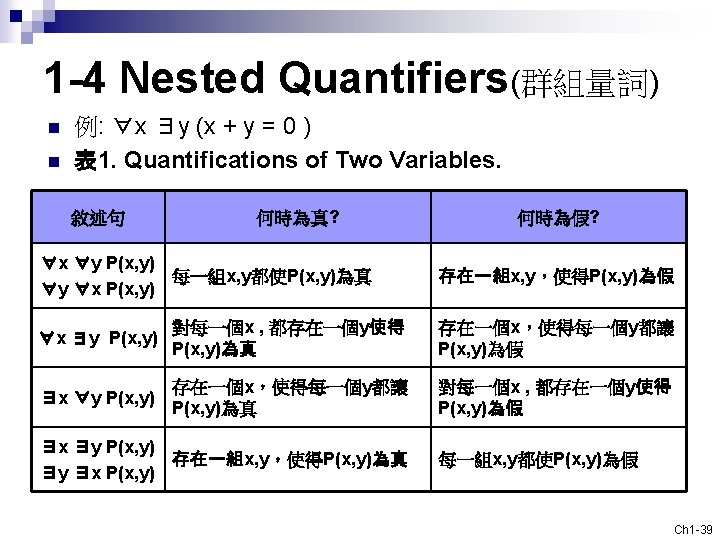
Example 1: 若Q(x, y)代表 “x = y + 3”，請問Q(1, 2)及Q(3, 0)的真值為何 ？ Sol: Q(1, 2) F Q(3, 0) T 量詞(quantifier) n n 命題中出現變數 x 時 the domain of x 指的是 x 的定義域，即範圍 Quantifiers : (數量詞，如 some，any，all 等) ∀ : universal quantifier (for all, for every, 所有的 ) ∃ : existential quantifier (there exist, there is, for some, 存在) Ch 1 -32

Example 11 : Let P(x) : x 2 < 10, when x ∈ Z+ (正整數), x ≤ 4. What is the truth value of x P(x) ? Sol : x ∈ {1, 2, 3, 4} ∴ 42 = 16 > 10 ∴ x P(x) is false. Example 16 : Let P(x) : x 2 > 10, when x ∈ Z+, x ≤ 4. What is the truth value of ∃x P(x) ? Sol : x ∈ {1, 2, 3, 4} ∴ 42 = 16 > 10 ∴ ∃x P(x) is true. Ch 1 -34

n 補充 : 習題52 “∃!” 表示 存在且唯一，只存在唯一的一個 ∃!x P(x) 表示 “存在唯一的一個x 使P(x)為真” Example : What is the truth values of the statements (a) ∃! x ( x 2 = 1 ) (b) ∃! x ( x + 3 = 2 x ) where x ∈ Z. Ans : (a) 12 = 1, (-1)2=1 False (b) x=3 is the only solution True Ch 1 -38

n Example : What is the truth values of the statements (a) ∀x ∀y (x + y ≥ 0), x, y ∈ N (自然數) T F (b) ∀x ∀y (xy = 0), x, y ∈ Z T (c) ∀x ∃y (x + y = 0), x, y ∈ Z F (d) ∀x ∃y (xy = -1), x, y ∈ Z T (e) ∃x ∀y (xy = 0), x, y ∈ Z F (f) ∃x ∀y (x + y = 0), x, y ∈ Z T (g) ∃x ∃y (xy = 0), x, y ∈ Z F (h) ∃x ∃y (x + y = ½), x, y ∈ Z Ch 1 -40