Discrete Math Lecture 4 Last week Sequences Definition

מתמטיקה בדידה Discrete Math Lecture 4

Last week: Sequences Definition: A sequence is a list of objects, called terms or components. Notation: (a, b, c, …) (a 1, a 2, a 3, …, an) Example: Fibonacci numbers (Italy ~1200 AD, India ~400 BC) (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …) Sequence Term/component סדרה אבר

Sequence vs. Set There are several key differences between sequences and sets. In a sequence: Terms are not required to be distinct 1. 2. (a, b, a) is a sequence of three terms {a, b, a} is a set of two elements Terms have a specified order 1. 2. (a, b, c) and (a, c, b) are different sequences {a, b, c} and {a, c, b} are the same set

Special Case: Ordered Pairs A sequence with two elements is called an ordered pair. Notation: (a, b) Fuctional definition: Two ordered pairs (a, b) and (c, d) are equal if and only if a=c and b=d. For the curious only: Can define an ordered pair (a, b) as {{a}, {a, b}} Special case Ordered pair מקרה פרטי זוג סדור

n-tuple and Prefix The definition of ordered pairs extends to: 1. 2. Ordered triple (a, b, c) Ordered quadruple (a, b, c, d) 3. Ordered n-tuple (a 1, a 2, …, an) (= sequence of length n. ) Definition: The n-tuple (b 1, b 2, …, bk) is called a prefix of (a 1, a 2, …, an) if and only if 1. k≤n 2. 8 i 2 {1, 2, …, k}, ai = bi Example: (1, 2, 7) is a prefix of (1, 2, 7, 11) n-tuple prefix יה סדורה -n רישא

Summary: Sequences Definition: A sequence is a list of objects, (a 1, a 2, a 3, …, an), called terms or components. Sequence vs Set: Terms are not required to be distinct 1. (a, b, a) is a sequence of three terms 2. {a, b, a} is a set of two elements Terms have a specified order 1. (a, b, c) and (a, c, b) are different sequences 2. {a, b, c} and {a, c, b} are the same set Definition: A sequence, (a, b), with two elements is called an ordered pair. Definition: A sequence, (a 1, a 2, …, an), with n elements is called an ordered n-tuple.

Cartesian Product of Two Sets Definition: The cartesian product of sets A and B is a new set consisting of all ordered pairs where 1. The first term is drawn from A 2. The second term is drawn from B In set-builder notation: Ax. B: ={(a, b)| a 2 A, b 2 B} Example: {1, 2}x{1, 3} = {(1, 1), (1, 3), (2, 1), (2, 3)} Cartesian product מכפלה קרטזית

Product of Sets Definition: A product of sets, S 1 x. S 2 x…x. Sn, is a new set consisting of all sequences where 1. The first term is drawn from S 1 2. The second term is drawn from S 2 and so on. . . In set-builder notation: Ax. B: ={(a, b)| a 2 A, b 2 B} S 1 x. S 2 x…x. Sn : = {(s 1, s 2, …, sn)| s 12 S 1, s 2 2 S 2, …, sn 2 Sn} Product מכפלה

Product of Sets Example: The set Nx{a, b} equals {(0, a), (0, b), (1, a), (1, b), (2, a), (2, b), …} A product of n copies of S is denoted Sn Example: The set {0, 1}3 equals {(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)}

Quick Question Write a program that does the following: Input: Two sets A = {a 1, …, an}, and B = {b 1, …, bm}. Output: The product C = Ax. B. For i = 1 to n For j = 1 to m (bj, ai) ci, j = (ai, bj) End For Output C = {c 1, 1, …, cn, m} What about a program that outputs Bx. A? Does the order of i and j matter?

Functions

Function f : A!B Definition: A function, f, from set A to set B associates an element f(a) 2 B with an element a 2 A. We require that for every a 2 A there exists a single b 2 B so that f(a) = b That is: 8 a 2 A, 8 b, b’ 2 B,

Function: Examples f : R!R defined as f(x) = 1/x 2 f(3) = 1/9 f : Strings ! N defined as f(x) = string length of x f(“aabd”) = 4 i A: A ! A defined as i. A (x) = x (the identity function on A) identity function פונקצית הזהות

Function: Examples 2 A: U ! {0, 1} defined as A (x) = 1 0 if x 2 A (the characteristic function of A) f : A!B defined as f(x) = c for some c 2 B characteristic function constant function פונקציה אופיינית פונקציה קבועה (a constant function)

Functions: Notation 1. Typically using letters f, g, h (other letters also possible. ) (Some functions have standard names – e. g. sin, | |, tg, √…). 2. When we write a) 3. f : A ! B, we mean: f maps elements from A to elements in B When we write f(a) = b (or f: a b), we mean: a) Domain Codomain f maps a 2 A to b 2 B. תחום טווח

Functions: Terminology f(a) = b b 2 B is the value (image) of f at the argument a 2 A domain codomain Example: f : Strings ! N Value Image Argument ערך תמונה קלט ארגומנט argument value f(“aabd”) = 4

Specifying a Function 2 1. Truth table 1 if x = y 0 if x = y P Q f (P, Q) T T F F F T T F F T 2. Cases f(x, y) = 3. Formula 4. f(x) = x 2 Procedure f(y) = length of left to right search of a 1 in y. f(0010) = 3 f(100) = 1 f(0000) = undefined f(P, Q) = [P ! Q] specification rule כלל התאמה

Specifying a Function To specify a function f we need to show the value of f at each element of the domain. Typically, we say something like: “Let f : A ! B be defined by f(x) = …” Remark: when we write “f(x) = …, ” we actually mean: “ 8 x 2 A, f(x) = …”

Equality of Functions Definition: Two functions, f and g, are equal if and only if 1. domain(f) = domain(g) 2. 8 x 2 domain(f), f(x) = g(x) we then write f = g. Example: If domain(f) = domain(g) = R and f(x) = (x+1)2 then f = g. g(x) = x 2 + 2 x + 1

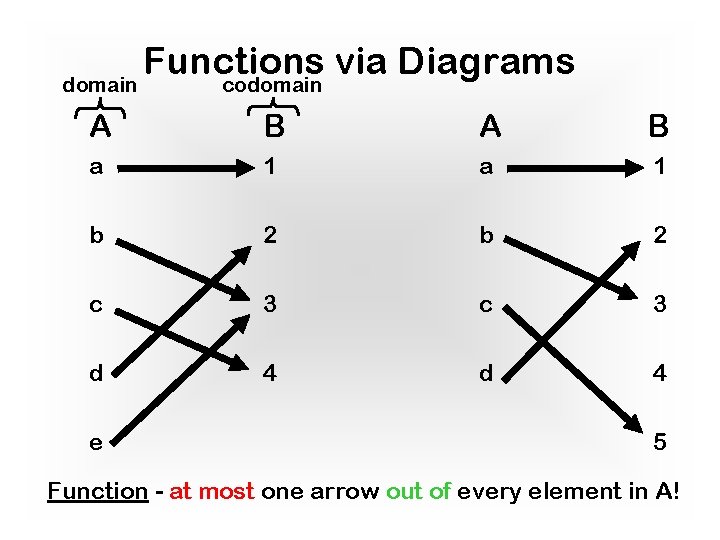
Functions via Diagrams codomain A B a 1 b 2 c 3 d 4 e 5 Function - at most one arrow out of every element in A!

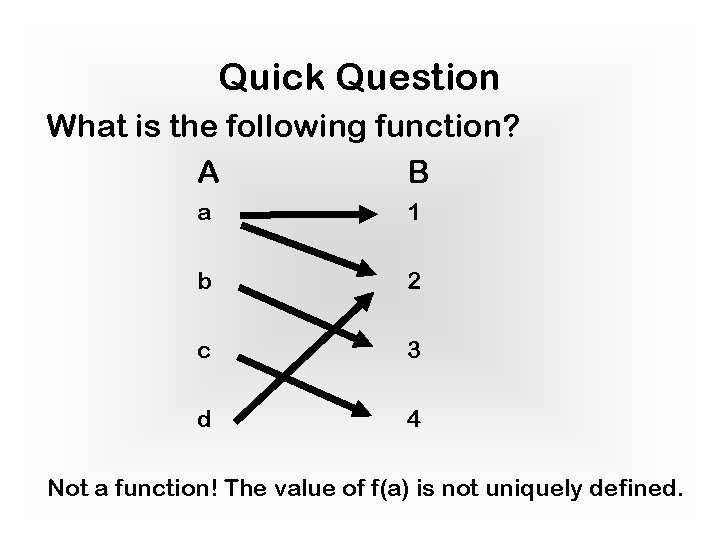
Quick Question What is the following function? A B a 1 b 2 c 3 d 4 Not a function! The value of f(a) is not uniquely defined.

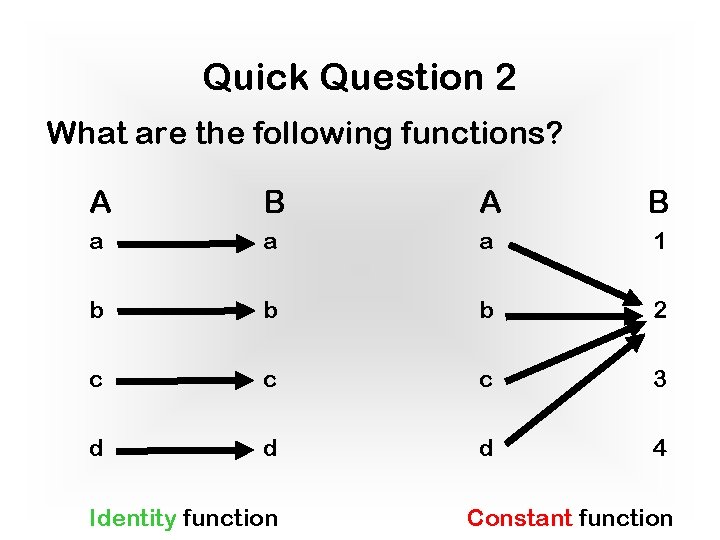
Quick Question 2 What are the following functions? A B a a a 1 b b b 2 c c c 3 d d d 4 Identity function Constant function

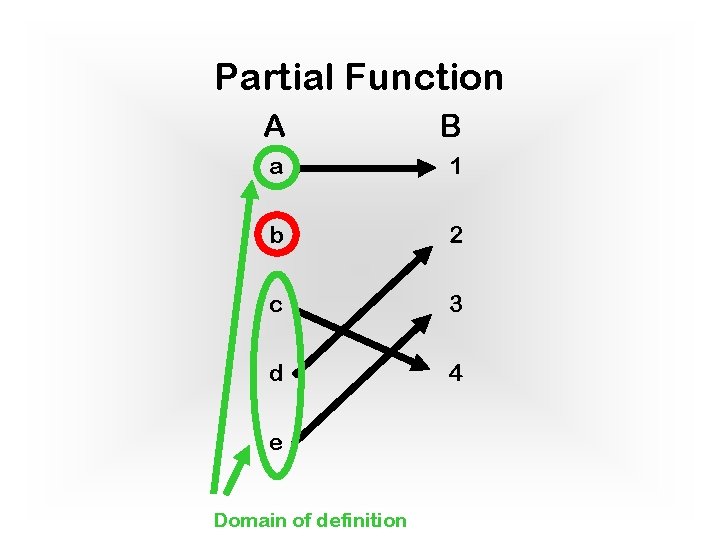
Domain of Definition: The domain of definition of f: A ! B is the set A’ A of values on which f is defined. Definition: A function f: A ! B is said to be partial if its domain of definition is a strict subset of its domain (that is, A’ A). Example: f : Rx R ! R A = Rx R Domain of definition Partial f(x, y) = 1/(x-y) A’ = Rx. R {(x, y) 2 Rx. R | x=y} תחום הגדרה חלקית

Partial Function A B a 1 b 2 c 3 d 4 e Domain of definition

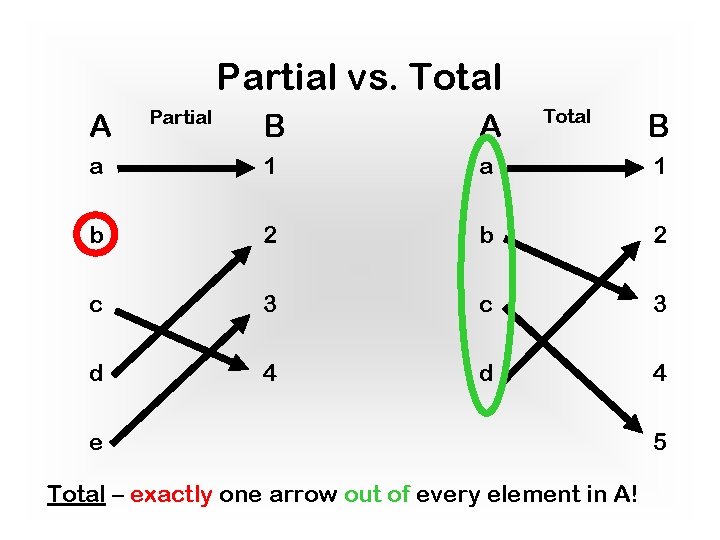
Total Function Definition: A function f: A ! B is said to be total if its domain of definition equals its domain (that is, A’ = A). That is: Examples: f : Rx. R {(x, y) 2 Rx. R | x=y} ! R f : N!N Total f(x, y) = 1/(x-y) f(x) = 2 x מלאה / טוטאלית

Partial vs. Total A Partial Total B A a 1 b 2 c 3 d 4 e Total – exactly one arrow out of every element in A! B 5

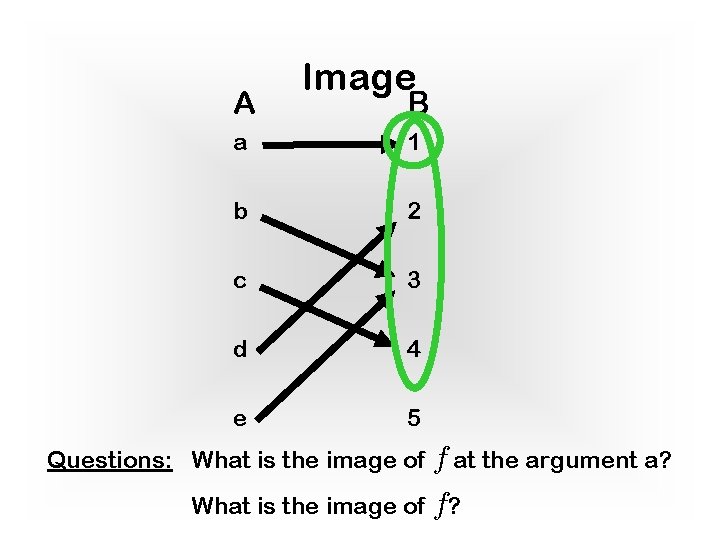
Image Terminology: b 2 B is the value (image) of f at the argument a 2 A Definition: The image of f is the set of all b 2 B that are the image/value of some element a 2 A. Image(f) : = {b 2 B | 9 a 2 A, f(a) = b} Sometimes also called range. argument image Example: f : N ! N f(x) = 2 x Value Image Argument ערך תמונה קלט ארגומנט Image(f) = Evens

A Image B a 1 b 2 c 3 d 4 e 5 Questions: What is the image of f at the argument a? What is the image of f?

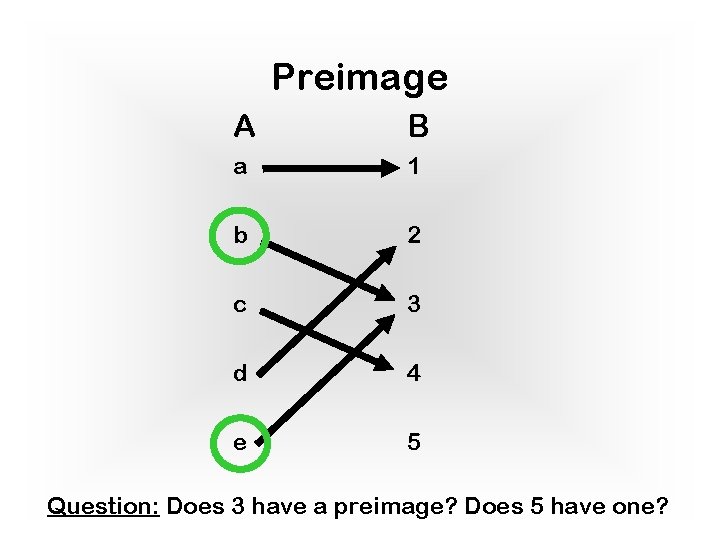
Functions: Preimage Terminology: a’ 2 A is the preimage of b under f if f(a’) = b An element b may have many preimages under f Example: f : Strings ! N 1. 2. What is the image (value) of “aabd”? Is the preimage of 4 unique? Preimage מקור f(“aabd”) = 4

Preimage A B a 1 b 2 c 3 d 4 e 5 Question: Does 3 have a preimage? Does 5 have one?

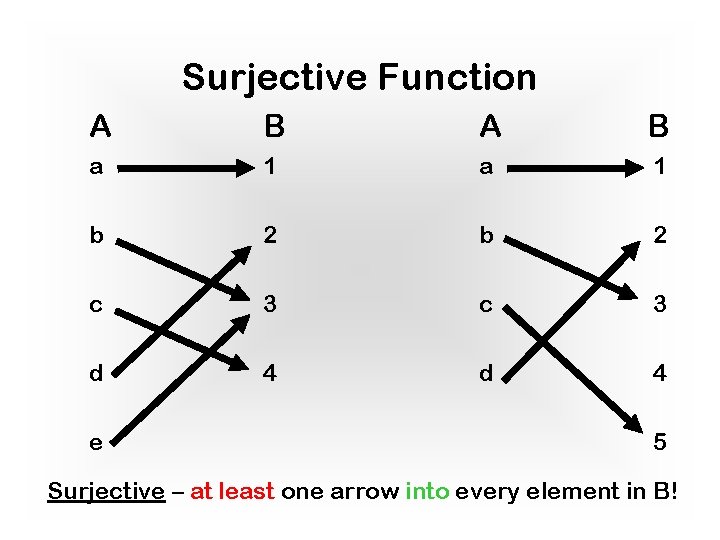
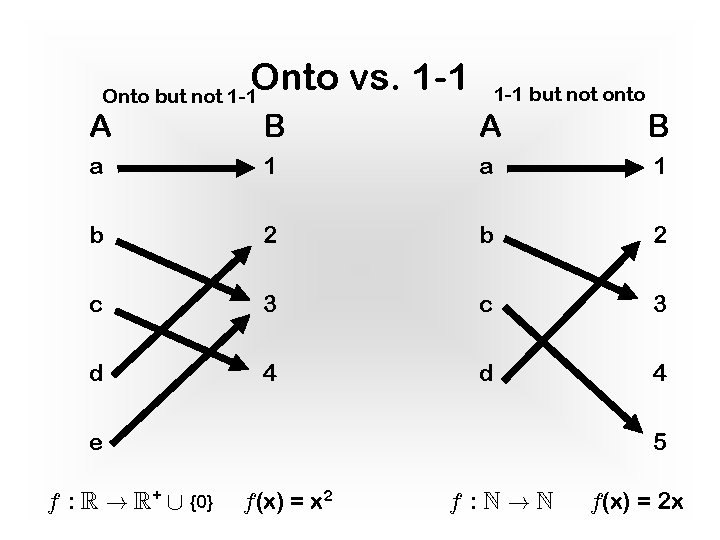
Surjection Definition: A function f: A ! B is a surjection iff every element of B is f of something (at least one a 2 A). In other words, 1. range(f) = B or, alternatively, 2. Example: f : R ! R+ [ {0} f(x) = x 2 Non-example: f : N!N f(x) = 2 x Surjective/onto על

Surjective Function A B a 1 b 2 c 3 d 4 e 5 Surjective – at least one arrow into every element in B!

Surjection A ! B means that |A| ≥ |B|

Injection Definition: A function f: A ! B is an injection iff every element of B is f of at most one a 2 A. In other words, (alternatively, ) f : N!N Example: f(x) = 2 x Non-example: f : Z!Z f(x) = x 2 Injective/one-to-one חד ערכית - חד

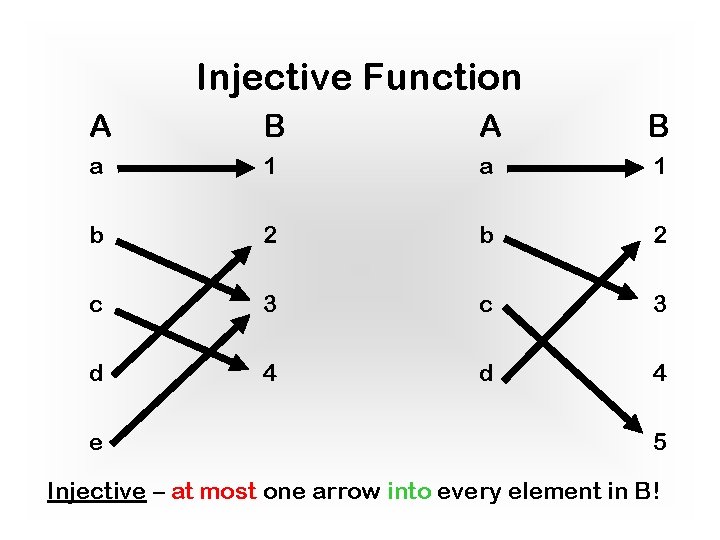
Injective Function A B a 1 b 2 c 3 d 4 e 5 Injective – at most one arrow into every element in B!

Injection A ! B means that Total |A| ≤ |B|

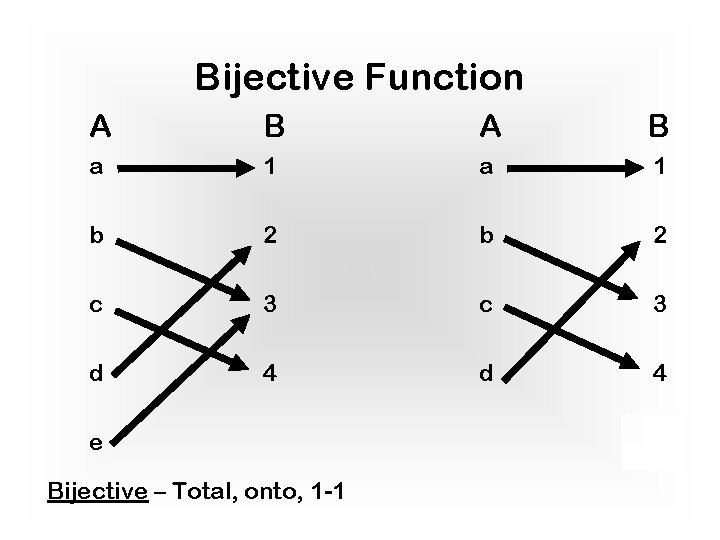
Bijection Definition: A function f: A ! B is a bijection iff it is all of the following: 1. Total 2. Onto (surjective) 3. 1 -1 (injective) Example: f : Evens ! N f(x) = x/2 Bijective חד ערכית ועל - חד

Bijective Function A B a 1 b 2 c 3 d 4 e Bijective – Total, onto, 1 -1 5

Bijection A ! B means that |A| = |B|

Summary We say a function f: A ! B is Total if every a 2 A is assigned to some b 2 B (and partial otherwise). Surjective if every b 2 B is mapped to at least once. Injective if every b 2 B is mapped to at most once. Bijective iff it is all of the above: 1. Total 2. Onto ( )על 3. 1 -1 ( )חד חד ערכית

Onto vs. 1 -1 Onto but not 1 -1 but not onto A B a 1 b 2 c 3 d 4 e f : R ! R+ [ {0} 5 f(x) = x 2 f : N!N f(x) = 2 x

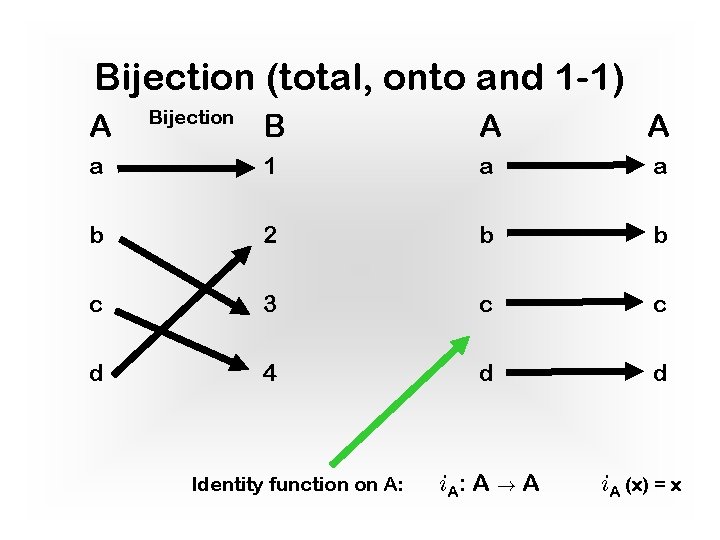
Bijection (total, onto and 1 -1) A Bijection B A A a 1 a a b 2 b b c 3 c c d 4 d d Identity function on A: i A: A ! A i. A (x) = x

The Mapping Rule Lemma: • If f: A ! B is surjective, then |A| ≥ |B|. • If f: A ! B is total and injective, then |A| ≤ |B|. • If f: A ! B is bijective, then |A| = |B|.

Working with the definitions Consider the following functions: • f : Nx. N !Z, f(x, y) = x-2 y. • g : Z !Z, g(x) = (x 2 + 1)/2. • h : P(A) !P(A) , h(X) = A X, where A : = {1, 2, 3, 4, 5}. Questions: For each of these functions, determine • • • What is the domain of definition and the image? Is the function partial or total? Is the function injective, surjective, bijective?

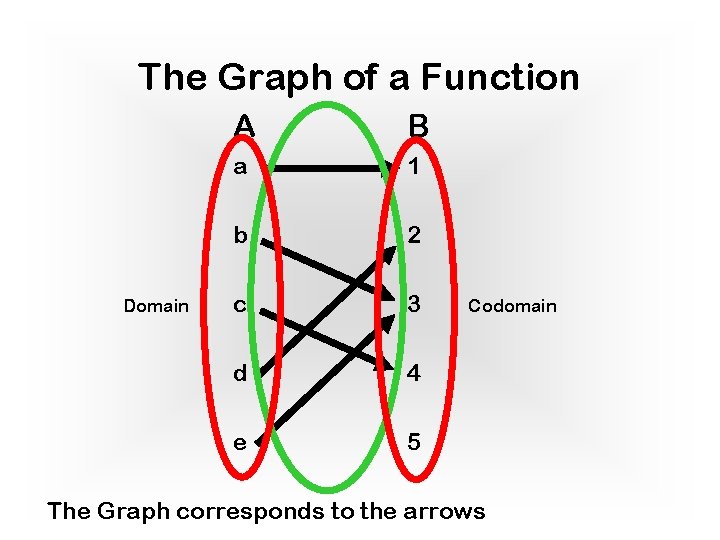
The Graph of a Function Everything about a function f is captured by 3 sets: 1. 2. The domain A, the codomain B, 3. the graph of f {(a, b) | f(a)=b} To tell if a function is 1. total we also need to know the domain 2. surjective we also need to know the codomain 3. 1 -1 we need to know the graph

The Graph of a Function Domain A B a 1 b 2 c 3 d 4 e 5 Codomain The Graph corresponds to the arrows

Formal Definition of a Function Definition: A function f from a set A to a set B is a set f Ax. B so that 8 a 2 A, 8 b, b’ 2 B, if (a, b) 2 f AND (a, b’) 2 f then b=b’ f (For every a 2 A, there exists a unique b 2 B so that (a, b) 2. ) (Recall: A x B = {(a, b) | a 2 A, b 2 B})