Chapter 1 Foundations Sets Logic and Algorithms Discrete

Chapter 1: Foundations: Sets, Logic, and Algorithms Discrete Mathematical Structures: Theory and Applications

Sets q Definition: Well-defined collection of distinct objects q Members or Elements: part of the collection q Roster Method: Description of a set by listing the elements, enclosed with braces q. Examples: q. Vowels = {a, e, i, o, u} q. Primary colors = {red, blue, yellow} q Membership examples q“a belongs to the set of Vowels” is written as: a Vowels q“j does not belong to the set of Vowels: j Vowels Discrete Mathematical Structures: Theory and Applications 2

Sets q Set-builder method q. A = { x | x S, P(x) } or A = { x S | P(x) } q A is the set of all elements x of S, such that x satisfies the property P q. Example: q. If X = {2, 4, 6, 8, 10}, then in set-builder notation, X can be described as X = {n Z | n is even and 2 n 10} Discrete Mathematical Structures: Theory and Applications 3

Sets q Standard Symbols which denote sets of numbers q N : The set of all natural numbers (i. e. , all positive integers) q Z : The set of all integers q Z* : The set of all nonzero integers q E : The set of all even integers q Q : The set of all rational numbers q Q* : The set of all nonzero rational numbers q Q+ : The set of all positive rational numbers q R : The set of all real numbers q R* : The set of all nonzero real numbers q R+ : The set of all positive real numbers q C : The set of all complex numbers q C* : The set of all nonzero complex numbers Discrete Mathematical Structures: Theory and Applications 4

Sets q Subsets q“X is a subset of Y” is written as X Y q“X is not a subset of Y” is written as X q. Example: Y q X = {a, e, i, o, u}, Y = {a, i, u} and z = {b, c, d, f, g} q. Y X, since every element of Y is an element of X q. Y Z, since a Y, but a Z q Superset q. X and Y are sets. If X Y, then “X is contained in Y” or “Y contains X” or Y is a superset of X, written Y X Discrete Mathematical Structures: Theory and Applications 5

Sets q Set Equality q. X and Y are sets. They are said to be equal if every element of X is an element of Y and every element of Y is an element of X, i. e. X Y and Y X q. Examples: q{1, 2, 3} = {2, 3, 1} q. X = {red, blue, yellow} and Y = {c | c is a primary color} Therefore, X=Y q Empty (Null) Set q. A Set is Empty (Null) if it contains no elements. q. The Empty Set is written as q. The Empty Set is a subset of every set Discrete Mathematical Structures: Theory and Applications 6

Sets q Finite and Infinite Sets q. X is a set. If there exists a nonnegative integer n such that X has n elements, then X is called a finite set with n elements. q. If a set is not finite, then it is an infinite set. q. Examples: q Y = {1, 2, 3} is a finite set q P = {red, blue, yellow} is a finite set q E , the set of all even integers, is an infinite set q , the Empty Set, is a finite set with 0 elements Discrete Mathematical Structures: Theory and Applications 7

Sets q Cardinality of Sets q. Let S be a finite set with n distinct elements, where n ≥ 0. Then |S| = n , where the cardinality (number of elements) of S is n q. Example: q. If P = {red, blue, yellow}, then |P| = 3 q. Singleton q A set with only one element is a singleton q. Example: q. H = { 4 }, |H| = 1, H is a singleton Discrete Mathematical Structures: Theory and Applications 8

Sets q Power Set q. For any set X , the power set of X , written P(X), is the set of all subsets of X q. Example: q. If X = {red, blue, yellow}, then P(X) = { , {red}, {blue}, {yellow}, {red, blue}, {red, yellow}, {blue, yellow}, {red, blue, yellow} } q Universal Set q. An arbitrarily (randomly) chosen, but fixed set Discrete Mathematical Structures: Theory and Applications 9

Sets q Union of Sets Example: If X = {1, 2, 3, 4, 5} and Y = {5, 6, 7, 8, 9}, then X∪Y = {1, 2, 3, 4, 5, 6, 7, 8, 9} Discrete Mathematical Structures: Theory and Applications 10

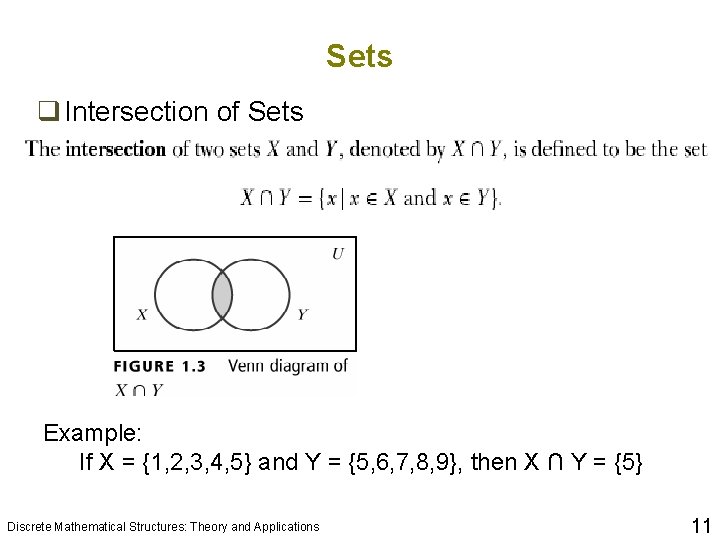
Sets q Intersection of Sets Example: If X = {1, 2, 3, 4, 5} and Y = {5, 6, 7, 8, 9}, then X ∩ Y = {5} Discrete Mathematical Structures: Theory and Applications 11

Sets q Disjoint Sets Example: If X = {1, 2, 3, 4, } and Y = {6, 7, 8, 9}, then X ∩ Y = Discrete Mathematical Structures: Theory and Applications 12

Sets Discrete Mathematical Structures: Theory and Applications 13

Sets Discrete Mathematical Structures: Theory and Applications 14

Sets q Example: q. If A = {a, b, c}, B = {x, y, z} and C = {1, 2, 3} then A ∩ B = and B ∩ C = and A ∩ C = . Therefore, A, B, C are pairwise disjoint Discrete Mathematical Structures: Theory and Applications 15

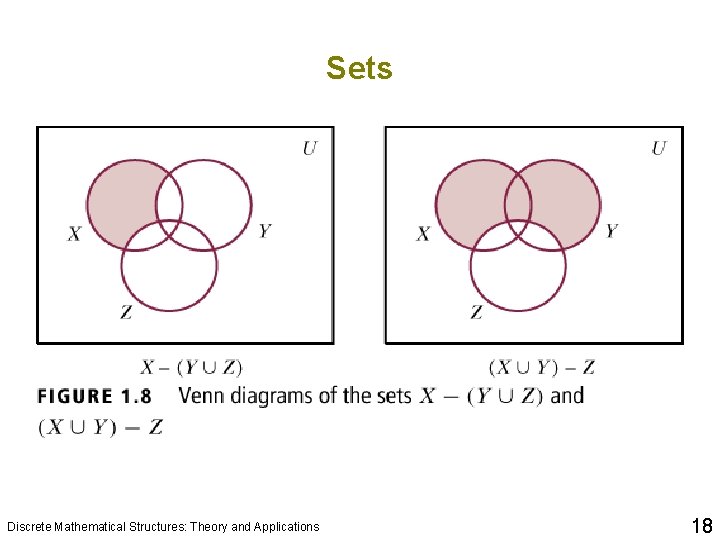
Sets q Difference • Example: If X = {a, b, c, d} and Y = {c, d, e, f}, then X – Y = {a, b} and Y – X = {e, f} Discrete Mathematical Structures: Theory and Applications 16

Sets q Complement Example: If U = {a, b, c, d, e, f} and X = {c, d, e, f}, then X’ = {a, b} Discrete Mathematical Structures: Theory and Applications 17

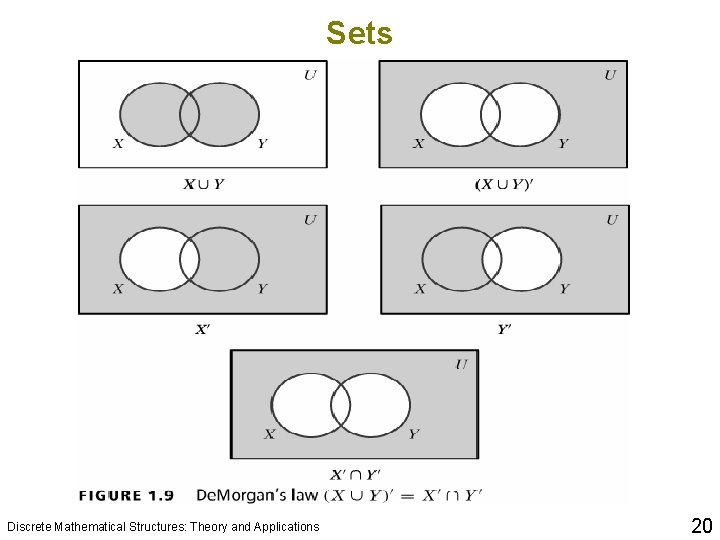
Sets Discrete Mathematical Structures: Theory and Applications 18

Sets Discrete Mathematical Structures: Theory and Applications 19

Sets Discrete Mathematical Structures: Theory and Applications 20

Sets q Ordered Pair q. X and Y are sets. If x X and y Y, then an ordered pair is written (x, y) q. Order of elements is important. (x, y) is not necessarily equal to (y, x) q Cartesian Product q The Cartesian product of two sets X and Y , written X × Y , is the set q X × Y ={(x, y)|x ∈ X , y ∈ Y} q. For any set X, X × = = × X q Example: q X = {a, b}, Y = {c, d} q. X × Y = {(a, c), (a, d), (b, c), (b, d)} q. Y × X = {(c, a), (d, a), (c, b), (d, b)} Discrete Mathematical Structures: Theory and Applications 21

Sets q Diagonal of a Set q. For a set X , the set δx , is the diagonal of X, defined by δx = {(x, x) | x ∈ X} q. Example: q X = {a, b, c}, δx = {(a, a), (b, b), (c, c)} Discrete Mathematical Structures: Theory and Applications 22

Sets q Computer Representation of Sets q. A Set may be stored in a computer in an array as an unordered list q. Problem: Difficult to perform operations on the set. q. Solution: use Bit Strings q. A Bit String is a sequence of 0 s and 1 s q. Length of a Bit String is the number of digits in the string q. Elements appear in order in the bit string q. A 0 indicates an element is absent, a 1 indicates that the element is present Discrete Mathematical Structures: Theory and Applications 23

Mathematical Logic q Definition: Methods of reasoning, provides rules and techniques to determine whether an argument is valid q Theorem: a statement that can be shown to be true (under certain conditions) q. Example: If x is an even integer, then x + 1 is an odd integer q. This statement is true under the condition that x is an integer is true Discrete Mathematical Structures: Theory and Applications 24

Mathematical Logic q A statement, or a proposition, is a declarative sentence that is either true or false, but not both q Lowercase letters denote propositions q. Examples: qp: 2 is an even number (true) qq: 3 is an odd number (true) qr: A is a consonant (false) q. The following are not propositions: qp: My cat is beautiful qq: Are you in charge? Discrete Mathematical Structures: Theory and Applications 25

Mathematical Logic q Truth value q One of the values “truth” or “falsity” assigned to a statement q True is abbreviated to T or 1 q False is abbreviated to F or 0 q Negation q The negation of p, written ∼p, is the statement obtained by negating statement p q. Truth values of p and ∼p are opposite q. Symbol ~ is called “not” ~p is read as as “not p” q. Example: qp: A is a consonant q~p: it is the case that A is not a consonant qq: Are you in charge? Discrete Mathematical Structures: Theory and Applications 26

Mathematical Logic q Truth Table q Conjunction q Let p and q be statements. The conjunction of p and q, written p ^ q , is the statement formed by joining statements p and q using the word “and” q. The statement p∧q is true if both p and q are true; otherwise p∧q is false Discrete Mathematical Structures: Theory and Applications 27

Mathematical Logic q Conjunction q. Truth Table for Conjunction: Discrete Mathematical Structures: Theory and Applications 28

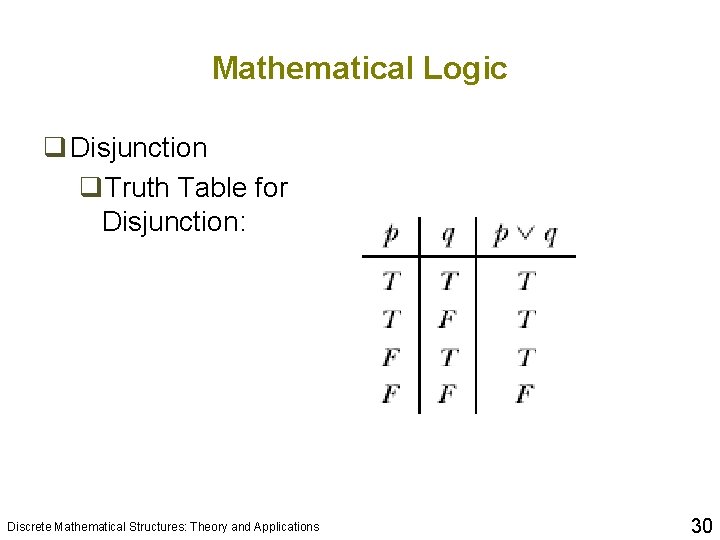
Mathematical Logic q Disjunction q. Let p and q be statements. The disjunction of p and q, written p ∨ q , is the statement formed by joining statements p and q using the word “or” q. The statement p∨q is true if at least one of the statements p and q is true; otherwise p∨q is false q. The symbol ∨ is read “or” Discrete Mathematical Structures: Theory and Applications 29

Mathematical Logic q Disjunction q. Truth Table for Disjunction: Discrete Mathematical Structures: Theory and Applications 30

Mathematical Logic q Implication q. Let p and q be statements. The statement “if p then q” is called an implication or condition. q. The implication “if p then q” is written p q qp q is read: q“If p, then q” q“p is sufficient for q” qq if p qq whenever p Discrete Mathematical Structures: Theory and Applications 31

Mathematical Logic q Implication q. Truth Table for Implication: qp is called the hypothesis, q is called the conclusion Discrete Mathematical Structures: Theory and Applications 32

Mathematical Logic q Implication q. Let p: Today is Sunday and q: I will wash the car. The conjunction p q is the statement: qp q : If today is Sunday, then I will wash the car q. The converse of this implication is written q p q. If I wash the car, then today is Sunday q. The inverse of this implication is ~p ~q q. If today is not Sunday, then I will not wash the car q. The contrapositive of this implication is ~q ~p q. If I do not wash the car, then today is not Sunday Discrete Mathematical Structures: Theory and Applications 33

Mathematical Logic q Biimplication q. Let p and q be statements. The statement “p if and only if q” is called the biimplication or biconditional of p and q q. The biconditional “p if and only if q” is written p q qp q is read: q“p if and only if q” q“p is necessary and sufficient for q” q“q if and only if p” q“q when and only when p” Discrete Mathematical Structures: Theory and Applications 34

Mathematical Logic q Biconditional q. Truth Table for the Biconditional: Discrete Mathematical Structures: Theory and Applications 35

Mathematical Logic q Statement Formulas q Definitions q Symbols p , q , r , . . . , called statement variables q Symbols ~, ∧, ∨, →, and ↔ are called logical connectives 1) A statement variable is a statement formula 2) If A and B are statement formulas, then the expressions (~A ), (A ∧ B) , (A ∨ B ), (A → B ) and (A ↔ B ) are statement formulas q Expressions are statement formulas that are constructed only by using 1) and 2) above Discrete Mathematical Structures: Theory and Applications 36

Mathematical Logic q Precedence of logical connectives is: q~ highest q∧ second highest q∨ third highest q→ fourth highest q↔ fifth highest Discrete Mathematical Structures: Theory and Applications 37

Mathematical Logic q Example: q. Let A be the statement formula (~(p ∨q )) → (q ∧p ) q. Truth Table for A is: Discrete Mathematical Structures: Theory and Applications 38

Mathematical Logic q Tautology q. A statement formula A is said to be a tautology if the truth value of A is T for any assignment of the truth values T and F to the statement variables occurring in A q Contradiction q. A statement formula A is said to be a contradiction if the truth value of A is F for any assignment of the truth values T and F to the statement variables occurring in A Discrete Mathematical Structures: Theory and Applications 39

Mathematical Logic q Logically Implies q. A statement formula A is said to logically imply a statement formula B if the statement formula A → B is a tautology. If A logically implies B, then symbolically we write A → B q Logically Equivalent q. A statement formula A is said to be logically equivalent to a statement formula B if the statement formula A ↔ B is a tautology. If A is logically equivalent to B , then symbolically we write A ≡ B (or A ⇔ B) Discrete Mathematical Structures: Theory and Applications 40

Mathematical Logic Discrete Mathematical Structures: Theory and Applications 41

Mathematical Logic q Proof of (~p ∧q ) → (~(q →p )) Discrete Mathematical Structures: Theory and Applications 42

Mathematical Logic q Proof of (~p ∧q ) → (~(q →p )) [Continued] Discrete Mathematical Structures: Theory and Applications 43

Validity of Arguments q Proof: an argument or a proof of a theorem consists of a finite sequence of statements ending in a conclusion q Argument: a finite sequence of statements. q The final statement, , is the conclusion, and the statements are the premises of the argument. q An argument is logically valid if the statement formula is a tautology. Discrete Mathematical Structures: Theory and Applications 44

Validity of Arguments q Valid Argument Forms q. Modus Ponens (Method of Affirming) q. Modus Tollens (Method of Denying) Discrete Mathematical Structures: Theory and Applications 45

Validity of Arguments q Valid Argument Forms q. Disjunctive Syllogisms Discrete Mathematical Structures: Theory and Applications 46

Validity of Arguments q Valid Argument Forms q Hypothetical Syllogism q Dilemma Discrete Mathematical Structures: Theory and Applications 47

Validity of Arguments q Valid Argument Forms q. Conjunctive Simplification Discrete Mathematical Structures: Theory and Applications 48

Validity of Arguments q Valid Argument Forms q. Disjunctive Addition Discrete Mathematical Structures: Theory and Applications 49

Validity of Arguments q Valid Argument Forms q. Conjunctive Addition Discrete Mathematical Structures: Theory and Applications 50

Quantifiers and First Order Logic q Predicate or Propositional Function q. Let x be a variable and D be a set; P(x) is a sentence q. Then P(x) is called a predicate or propositional function with respect to the set D if for each value of x in D, P(x) is a statement; i. e. , P(x) is true or false q. Moreover, D is called the domain of the discourse and x is called the free variable Discrete Mathematical Structures: Theory and Applications 51

Quantifiers and First Order Logic q Predicate or Propositional Function q. Example: q Q(x, y) : x > y, where the Domain is the set of integers q Q is a 2 -place predicate q Q is T for Q(4, 3) and Q is F for Q (3, 4) Discrete Mathematical Structures: Theory and Applications 52

Quantifiers and First Order Logic q Universal Quantifier q. Let P(x) be a predicate and let D be the domain of the discourse. The universal quantification of P(x) is the statement: q. For all x, P(x) or q. For every x, P(x) q. The symbol is read as “for all and every” q q Two-place predicate: Discrete Mathematical Structures: Theory and Applications 53

Quantifiers and First Order Logic q Existential Quantifier q. Let P(x) be a predicate and let D be the domain of the discourse. The existential quantification of P(x) is the statement: q. There exists x, P(x) q. The symbol is read as “there exists” q q Bound Variable q. The variable appearing in: Discrete Mathematical Structures: Theory and Applications or 54

Quantifiers and First Order Logic q Negation of Predicates (De. Morgan’s Laws) q q. Example: q If P(x) is the statement “x has won a race” where the domain of discourse is all runners, then the universal quantification of P(x) is , i. e. , every runner has won a race. The negation of this statement is “it is not the case that every runner has won a race. Therefore there exists at least one runner who has not won a race. Therefore: and so, Discrete Mathematical Structures: Theory and Applications 55

Quantifiers and First Order Logic q. Negation of Predicates (De. Morgan’s Laws) q Discrete Mathematical Structures: Theory and Applications 56

Quantifiers and First Order Logic q Formulas in Predicate Logic q. All statement formulas are considered formulas q. Each n, n =1, 2, . . . , n-place predicate P( ) containing the variables is a formula. q. If A and B are formulas, then the expressions ~A, (A∧B), (A∨B) , A →B and A↔B are statement formulas, where ~, ∧, ∨, → and ↔ are logical connectives q. If A is a formula and x is a variable, then ∀x A(x) and ∃x A(x) are formulas q. All formulas constructed using only above rules are considered formulas in predicate logic Discrete Mathematical Structures: Theory and Applications 57

Quantifiers and First Order Logic q Additional Rules of Inference q. If the statement ∀x P(x) is assumed to be true, then P(a) is also true, where a is an arbitrary member of the domain of the discourse. This rule is called the universal specification (US) q. If P(a) is true, where a is an arbitrary member of the domain of the discourse, then ∀x P(x) is true. This rule is called the universal generalization (UG) q. If the statement ∃x P (x) is true, then P(a) is true, for some member of the domain of the discourse. This rule is called the existential specification (ES) q. If P(a) is true for some member a of the domain of the discourse, then ∃x P(x) is also true. This rule is called the existential generalization (EG) Discrete Mathematical Structures: Theory and Applications 58

Quantifiers and First Order Logic q Counterexample q. An argument has the form ∀x (P(x ) → Q(x )), where the domain of discourse is D q. To show that this implication is not true in the domain D, it must be shown that there exists some x in D such that (P(x ) → Q(x )) is not true q. This means that there exists some x in D such that P(x) is true but Q(x) is not true. Such an x is called a counterexample of the above implication q. To show that ∀x (P(x) → Q(x)) is false by finding an x in D such that P(x) → Q(x) is false is called the disproof of the given statement by counterexample Discrete Mathematical Structures: Theory and Applications 59

Proof Techniques q Theorem q. Statement that can be shown to be true (under certain conditions) q. Typically Stated in one of three ways q. As Facts q. As Implications q. As Biimplications Discrete Mathematical Structures: Theory and Applications 60

Proof Techniques q Direct Proof or Proof by Direct Method q. Proof of those theorems that can be expressed in the form ∀x (P(x) → Q(x)), D is the domain of discourse q. Select a particular, but arbitrarily chosen, member a of the domain D q. Show that the statement P(a) → Q(a) is true. (Assume that P(a) is true q. Show that Q(a) is true q. By the rule of Universal Generalization (UG), ∀x (P(x) → Q(x)) is true Discrete Mathematical Structures: Theory and Applications 61

Proof Techniques q Indirect Proof q. The implication p → q is equivalent to the implication (∼q → ∼p) q. Therefore, in order to show that p → q is true, one can also show that the implication (∼q → ∼p) is true q. To show that (∼q → ∼p) is true, assume that the negation of q is true and prove that the negation of p is true Discrete Mathematical Structures: Theory and Applications 62

Proof Techniques q Proof by Contradiction q. Assume that the conclusion is not true and then arrive at a contradiction q. Example: Prove that there are infinitely many prime numbers q. Proof: q. Assume there are not infinitely many prime numbers, therefore they are listable, i. e. p 1, p 2, …, pn q. Consider the number q = p 1 p 2…pn+1. q is not divisible by any of the listed primes q. Therefore, q is a prime. However, it was not listed. q. Contradiction! Therefore, there are infinitely many primes Discrete Mathematical Structures: Theory and Applications 63

Proof Techniques Discrete Mathematical Structures: Theory and Applications 64

Proof Techniques q Proof of Biimplications q. To prove a theorem of the form ∀x (P(x) ↔ Q(x )), where D is the domain of the discourse, consider an arbitrary but fixed element a from D. For this a, prove that the biimplication P(a) ↔ Q(a) is true q. The biimplication p ↔ q is equivalent to (p → q) ∧ (q → p) q. Prove that the implications p → q and q → p are true q. Assume that p is true and show that q is true q. Assume that q is true and show that p is true Discrete Mathematical Structures: Theory and Applications 65

Proof Techniques q Proof of Equivalent Statements q. Consider theorem that says that statements p, q and r are equivalent q. Show that p → q, q → r and r → p q. Assume p and prove q. Then assume q and prove r Finally, assume r and prove p q. Or, prove that p if and only if q, and then q if and only if r q. Other methods are possible Discrete Mathematical Structures: Theory and Applications 66

Algorithms q Definition: step-by-step problem-solving process in which a solution is arrived at in a finite amount of time q All algorithms have the following properties: q. Input : For example, a set of numbers to find the sum of the numbers q. Output : For example, the sum of the numbers q. Precision : Each step of the algorithm is precisely defined q. Uniqueness : Results of each step are unique and depend on the input and results of previous step q. Finiteness : Algorithm must terminate after executing a finite number of steps q. Generality : Algorithm is general in that it applies to a set of inputs Discrete Mathematical Structures: Theory and Applications 67

Algorithms q Pseudocode Conventions q The symbol : = is called the assignment operator q. Example: The statement x : = a is read as “assign the value a to x” or “x gets the value a” or “copy the value of a into x” qx : = a is also known as an assignment statement q Control Structures q. One way-selection qif boolean. Expression then statement q. If boolean. Expression evaluates to true, statement is evaluated q. Two way-selection qif boolean. Expression then statement 1 else statement 2 q. If boolean. Expression evaluates to true , statement 1 executes, qotherwise statement 2 executes Discrete Mathematical Structures: Theory and Applications 68

Algorithms q Pseudocode Conventions q Control Structures q. The while loop takes the form: qwhile boolean. Expression do loop. Body q. The boolean. Expression is evaluated. If it evaluates to true, loop. Body executes. Thereafter loop. Body continues to execute as long as boolean. Expression is true q. The for loop takes the form: qfor var : = start to limit do loop. Body qvar is an integer variable. The variable var is set to the value specified by start. If var limit, loop. Body executes. After executing the loop. Body , var is incremented by 1. The statement continues to execute until var > limit Discrete Mathematical Structures: Theory and Applications 69

Algorithms q Pseudocode Conventions q. Control Structures q. The do/while loop takes the form: qdo loop. Body while boolean. Expression q. The loop. Body is executed first and then the boolean. Expression is evaluated. The loop. Body continues to execute as long as the boolean. Expression is true Discrete Mathematical Structures: Theory and Applications 70

Algorithms q Pseudocode Conventions q. Block of Statement q. To consider a set of statements a single statement, the statements are written between the words begin and end begin statement 1 statement 2. . . statementn; end Discrete Mathematical Structures: Theory and Applications 71

Algorithms q Pseudocode Conventions q. Return Statement q. The return statement is used to return the value computed by the algorithm and it takes the following form: return expression; q. The value specified by expression is returned. In an algorithm, the execution of a return statement also terminates the algorithm q. Read and Print Statements qread x; q. Read the next value and store it in the variable x qprint x; q. Output the value of x Discrete Mathematical Structures: Theory and Applications 72

Algorithms q Pseudocode Conventions q. Arrays (List) q. A list is a set of elements of the same type q. The length of the list is the number of elements in the list q. L[1. . . n ]. L is an array of n components, indexed 1 to n. L[i ] denotes the ith element of L q. For data in tabular form, a two-dimensional array is used: q. M[1. . . m, 1. . . n ] M is a two-dimensional array of m rows and n columns q. The rows are indexed 1 to m and the columns are indexed 1 to n q. M[i, j] denotes the (i, j)th element of M, that is, the element at the ith row and jth column position Discrete Mathematical Structures: Theory and Applications 73

Algorithms q Pseudocode Conventions q Subprograms (Procedures) q. In a programming language, an algorithm is implemented in the form of a subprogram, a. k. a. a subroutine or a module q. Two types of subprograms q. Functions q. Returns a unique value q. Procedure q. Other types of subprograms qbody of the function or procedure is enclosed between the words begin and end qthe execution of a return statement in a function terminates the function Discrete Mathematical Structures: Theory and Applications 74

Algorithms q Pseudocode Conventions q Comments q. In describing the steps of an algorithm, comments are included wherever necessary to clarify the steps q. Two types of comments: single-line and multi-line q. Single-line comments start anywhere in the line with the pair of symbols // q. Multi-line comments are enclosed between the pair of symbols /* and */ q. Specifies what the algorithm does, as well as the input and output Discrete Mathematical Structures: Theory and Applications 75

Algorithms q Polynomial Operations q Polynomial in one variable is q ai are real (or complex) and n is a non-negative integer q If p(x) = a 0 then p(x) is a constant polynomial q If p(x) is a nonzero constant polynomial, then the degree of p(x) is defined to be 0 q If p(x) is not constant and an 0, then n is called the degree of p(x); that is, the degree of a non-constant polynomial is defined to be the exponent of the highest power of x q The basic operations performed on polynomials are to add, subtract, multiply, and divide polynomials, and to evaluate a polynomial at a given point Discrete Mathematical Structures: Theory and Applications 76