DETERMINAN 1 DETERMINAN Untuk setiap matriks persegi A

DETERMINAN 1

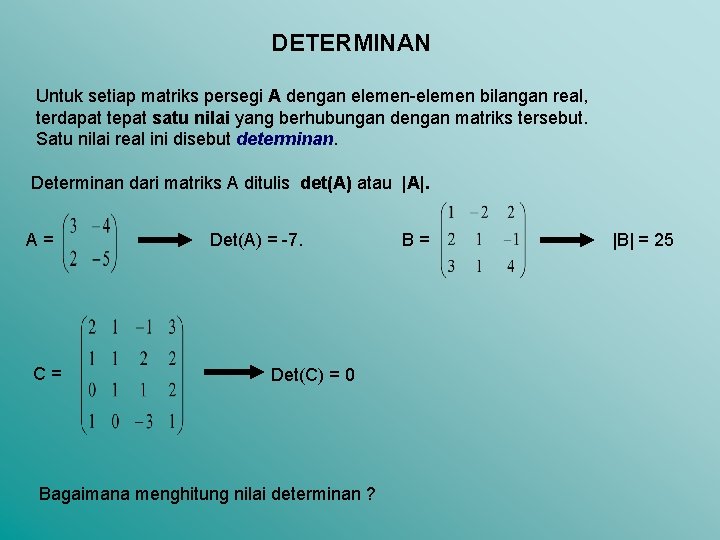
DETERMINAN Untuk setiap matriks persegi A dengan elemen-elemen bilangan real, terdapat tepat satu nilai yang berhubungan dengan matriks tersebut. Satu nilai real ini disebut determinan. Determinan dari matriks A ditulis det(A) atau |A|. A= C= Det(A) = -7. Det(C) = 0 Bagaimana menghitung nilai determinan ? B= |B| = 25

1. Definisi determinan Cara menghitung determinan : 2. Sifat-sifat determinan 3. Ekspansi minor dan kofaktor 4. Kombinasi cara 2 dan 3 MELALUI DEFINISI DETERMINAN Determinan : produk (hasil kali) bertanda dari unsur-unsur matriks sedemikian hingga berasal dari baris dan kolom yang berbeda, kemudian hasilnya dijumlahkan. A= Det(A) = a 11 a 22 – a 12 a 21 Bagaimana menentukan tanda + dan – tiap suku ?

Urutan natural (asli) : 1 A= 2 3 4 5 6. . . |A| = a 11 a 22 a 33 – a 11 a 23 a 32 + a 12 a 23 a 31 – a 12 a 21 a 33 + a 13 a 21 a 32 – a 13 a 22 a 31 Produk yg berasal dari baris dan kolom yg berbeda : a 11 a 22 a 33 Indeks kolom 1 2 3, sudah urut. Tidak ada transposisi. a 11 a 23 a 32 Indeks kolom 1 3 2, belum urut. Satu kali pindah. 1 2 3 a 12 a 23 a 31 Indeks kolom 2 3 1, belum urut. Dua kali pindah. 1 3 2 dan 1 2 3 a 12 a 21 a 33 Indeks kolom 2 1 3, belum urut. Satu kali pindah. 1 2 3 a 13 a 21 a 32 Indeks kolom 3 1 2, belum urut. Dua kali pindah. 2 1 3 dan 1 2 3 a 13 a 22 a 31 Indeks kolom 3 2 1, belum urut. Satu kali pindah. 1 2 3 Perhatikan, indeks baris sudah dalam urutan natural, indeks kolom belum. Tanda + atau – ditentukan banyaknya langkah (transposisi) yg membawa indeks kolom ke urutan natural. Jika genap +, jika ganjil (-) negatif; atau tandanya adalah (-1)t, dengan t banyaknya transposisi.

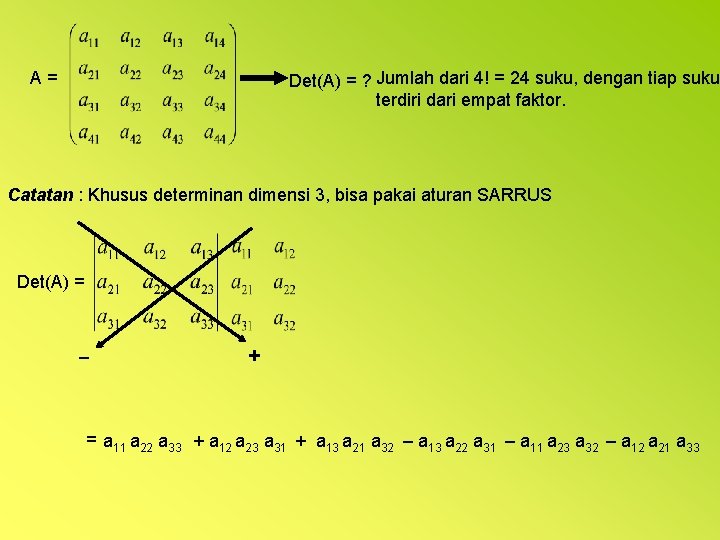
A= Det(A) = ? Jumlah dari 4! = 24 suku, dengan tiap suku terdiri dari empat faktor. Catatan : Khusus determinan dimensi 3, bisa pakai aturan SARRUS Det(A) = – + = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 – a 13 a 22 a 31 – a 11 a 23 a 32 – a 12 a 21 a 33

|A| = |B| = |C| = = 26 =– 6 =0 Dengan bantuan sifat determinan, membantu memudahkan menghitung nilai determinan.

SIFAT-SIFAT DETERMINAN 1. Determinan dari matriks dan transposenya adalah sama; |AT| = |A| = = 26 |AT| = = 26 Akibatnya : semua sifat determinan berlaku secara baris / dan secara kolom. 2. Matriks persegi yang mempunyai baris (kolom) nol, determinannya nol (0). det(B) = =0 det(C) = =0

3. Determinan dari suatu matriks persegi A yang salah satu baris (kolom) dikalikan dengan skalar k, maka determinannya berubah menjadi k A Jika baris kedua dikalikan dengan 7 |A| = = 35 = 7 |A| = 5 Akibat sifat ini : =7 = 7 (5) = 35 Suatu determinan jika salah satu baris (kolom) mempunyai faktor yang sama, maka sudah dapat difaktorkan. =3 =4

4. Determinan suatu matriks yang salah satu baris (kolom) nya ditukar dengan baris (kolom) yang lain, maka nilai determinan matriks tersebut berubah menjadi negatip determinan semula. = 31 Baris pertama ditukar baris kedua = – 31 5. Determinan dari suatu matriks persegi yang mempunyai dua baris (kolom) yang sama adalah sama dengan 0 (nol). =0 =0

6. Determinan dari suatu matriks persegi yang salah satu barisnya (kolomnya) merupakan kelipatan dari baris (kolom) yang lain adalah sama dengan 0 (nol). |B| = Karena kolom ke dua kelipatan kolom ke empat, |B| = 0 7. Determinan dari matriks persegi A = (aij) berdimensi n yang baris ke -i (kolom ke-j) terdiri dari elemen-elemen yang dapat diuraikan menjadi dua suku binomium, maka determinannya sama dengan determinan A yang baris ke-i (kolom ke-j) diganti dengan suku binomium yang pertama ditambah determinan A yang baris ke-i (kolom ke-j) diganti dengan suku yang kedua. = = + +

8. Determinan suatu matriks persegi tidak berubah nilainya jika salah satu baris (kolom) ditambah dengan kelipatan baris (kolom) yang lain. = 11 Jika k 2 + 3 k 1 Jika b 1 – b 2 = 11 Sifat ke 8 ini sering dipakai untuk menyederhanakan baris (kolom), sebelum menghitung nilai determinan = 11 9. Determinan dari matriks segitiga adalah sama dengan produk (hasil kali) elemen-elemen diagonalnya. = (3)(-1)(5) = - 15 = (-3)(-2)(4)(1) = 24

Gunakan sifat determinan untuk menghitung : b 2 + 3 b 1 b 3 – 2 b 1 = (1)(-1)(3) = - 3 Petunjuk umum : Gunakan sifat ke 8, untuk mereduksi matriks menjadi matriks segitiga; kemudian gunakan sifat ke 9 b 3 + 3 b 2

Submatriks / matriks bagian : Matriks yang diperoleh dengan menghilangkan beberapa baris dan/atau beberapa kolom dari suatu matriks A= Menghilangkan baris pertama diperoleh submatriiks : Menghilangkan baris kedua dan kolom ketiga diperoleh submatriks : dan sebagainya.

Minor dan Kofaktor Andaikan A berdimensi n, determinan dari submatriks yg berdimensi (n-1) disebut minor. Mrs : minor dari submatriks dng menghilangkan baris ke r kolom ke s. a 11 Andaikan A = M 11 = a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 22 a 23 a 32 a 33 M 32 = = a 22 a 33 – a 23 a 32 a 11 a 13 a 21 a 23 = a 11 a 23 – a 13 a 21 Untuk matriks A berdimensi 3 tersebut ada berapa minor ? Matriks tersebut mempunyai 9 minor

Kofaktor yang berhubungan dengan minor Mrs adalah Crs = (-1)r+s Mrs. A= C 11 = (-1)1+1 M 11 = (-1)2 = 1 (7) = 7 C 23 = - M 23 = 0 C 31 = M 31 = 7 C 12 = (-1)1+2 M 12 = (-1)3 C 13 = (-1)4 M 13 = = (-1) (9) = -9 =5 C 32 = - M 32 = - 9 C 33 = M 33 = 5 C 21 = (-1)3 M 21 = - M 21 = C 22 = M 22 = 0 =0

Menghitung determinan dengan ekspansi kofaktor : A= Ekspansi melalui baris pertama : Det(A) = a 11 C 11 + a 12 C 12 + a 13 C 13 Atau ekspansi melalui baris ketiga : Det(A) = a 31 C 31 + a 32 C 32 + a 33 C 33 Atau ekspansi melalui kolom ke dua : Det(A) = a 12 C 12 + a 22 C 22 + a 32 C 32 Dan sebagainya.

Dengan ekspansi kofaktor, hitung determinan : B= Andaikan dilakukan ekspansi melalui baris kedua : Det(B) = b 21 C 21 + b 22 C 22 + b 23 C 21 Det(B) = (3)(9) + (1)(3) + (-1) (-3) Det(B) = 33 = - M 21 = - C 22 = M 22 = 3 C 23 = - M 23 = - 3 Atau jika dikerjakan dengan ekspansi melalui kolom ketiga : Det(B) = b 13 C 13 + b 23 C 23 + b 33 C 13 = M 13 = 2 Det(B) = (1)(2) + (-1)(-3) + (4)(7) C 23 = - M 23 = - 3 Det(B) = 33 C 33 = M 33 = 7 =9

Strategi menghitung determinan : 1. Gunakan kombinasi beberapa metode (definisi, sifat, ekspansi kofaktor). 2. Pilih ekspansi melalui baris atau kolom yang paling sederhana. 3. Gunakan sifat ke 8 untuk membuat unsur-unsur pada baris/kolom yang dipilih sebanyak mungkin menjadi nol. 4. Ulangai langkah 1, dan seterusnya.

Hitung determinan dari : E = Dikerjakan dengan ekspansi melalui baris ke dua : |E| = K 2 + K 1 K 3 – K 1 |E| = e 21 C 21 + e 22 C 22 + e 23 C 23 |E| = e 21 C 21 + 0 |E| = (1) (-24) = - 24 C 21 = - M 21 = - {(3)(-7) – (-5)(9)} = - 24

Berapakah determinan dari F = Dipilih ekspansi melalui kolom pertama : |F| = B 3 + B 1 Det(F) = f 11 C 11 = (1) (6) = 6

Berapakah determinan dari G = Dipilih ekspansi melalui kolom ke tiga : Det(G) = B 2 + B 1 B 3+B 1 B 3 – B 2 Det(G) = g 13 C 13 = g 13 M 13 = (-1) Det(G) = (-1) g 21 C 21 = (-1) g 21 (- M 21) = g 21 M 21 = (3) {(4)(-5) – (7)(-5)} Det(G) = (3) (15) = 45.

Matriks kofaktor : Matriks yang anggota-anggotanya berupa kofaktor suatu matriks. A= C 11 = M 11 = -5 C 12 = - M 12 = - 4 Jadi matriks kofaktor dari A adalah : K = Matriks adjoint : Transpose dari matriks kofaktor. Adj (A) = KT = = C 21 = - M 21 = - 2 C 22 = M 22 = 3 =

Hitung (a) adjoint dari matriks A, (b) determinan matriks A A= C 11 = M 11 = 2 C 21 = -M 21 = 4 C 31 = M 31 = -1 C 12 = -M 12 = - 5 C 22 = M 22 = -1 C 32 = -M 32 = 7 C 13 = M 13 = - 1 C 23 = -M 23 = -2 C 33 = M 33 = 5 = (a) adj(A) = KT = = (b) Det(A) = a 11 C 11 + a 12 C 12 + a 13 c 13 = (1)(2) + (-2)(-5) + (3)(-1) = 9 A adj(A) = ? = = 9 = |A| I

Adj(A) A = ? = = 9 Sifat : 1. A adj(A) = adj(A) A = det(A) I 2. adj(AB) = adj(B) adj(A) = |A| I