PERTEMUA KE 4 Determinan dengan metode Ekspansi Laplace

PERTEMUA KE - 4 • • Determinan dengan metode Ekspansi Laplace Invers Matriks (Sifat-sifat), dan Aturan Cramer Kombinasi Linier

DETERMINAN DENGAN EKSPANSI KOFAKTOR • Jika A adalah matriks persegi dan minor dari komponen aij adalah Mij dan di definisikan sebagai determinan sub matriks A. dan Cij adalah kofaktor dari matriks A. • Contoh :

MINOR • Jika A adalah matriks persegi dan minor dari komponen aij adalah Mij dan di definisikan sebagai determinan sub matriks A. dan Cij adalah kofaktor dari matriks A. • Contoh :

KOFAKTOR • Jika A adalah matriks persegi dan minor dari komponen aij adalah Mij dan di definisikan sebagai determinan sub matriks A. dan Cij adalah kofaktor dari matriks A. • Contoh :

DETERMINAN EKSPANSI KOFAKTOR • Determinan dari suatu matriks A dengan ordo nxn dapat dihitung dengan perkalian antara komponen matriks A dan kofaktornya pada satu kolom atau baris, untuk setiap 1 ≤ i ≤ n dan 1 ≤ j ≤ n : • Ekspansi Kolom ke j : • Ekspansi Baris ke i :

TEOREMA • Jika A adalah matriks triangular (matriks segitiga atas, matriks segitiga bawah atau matriks diagonal), maka det(A) adalah perkalian dari komponen diagonal matriks A :

TEOREMA • Jika A adalah matriks persegi dan jika A memiliki komponen baris dan kolom adalah nol maka det(A)= 0 • Jika A adalah matriks persegi. Maka • Jika B adalah matriks dengan ordo nxn dan E adalah matriks dengan elemen nxn, maka : det(EB) = det(E) det(B) • Jika A adalah matriks yang dapat di inverskan/invertible jika dan hanya jika det(A) tidak sama dengan 0

LATIHAN • Tentukan determinan Matriks A dan B dan invers Matriks A dan B, Jika :

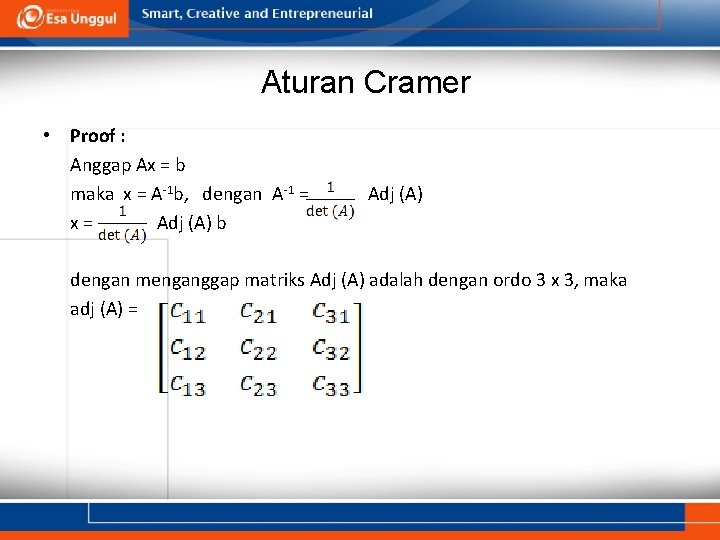
Aturan Cramer • Proof : Anggap Ax = b maka x = A-1 b, dengan A-1 = Adj (A) x = Adj (A) b dengan menganggap matriks Adj (A) adalah dengan ordo 3 x 3, maka adj (A) =

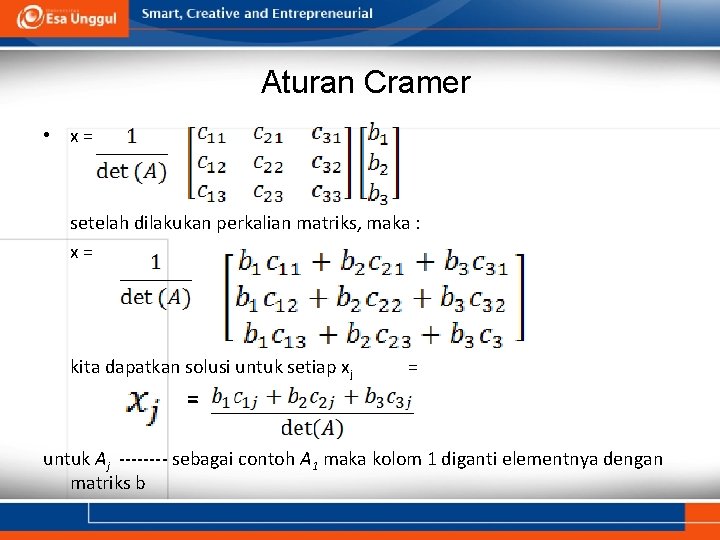
Aturan Cramer • x = setelah dilakukan perkalian matriks, maka : x = kita dapatkan solusi untuk setiap xj = = untuk Aj ---- sebagai contoh A 1 maka kolom 1 diganti elementnya dengan matriks b

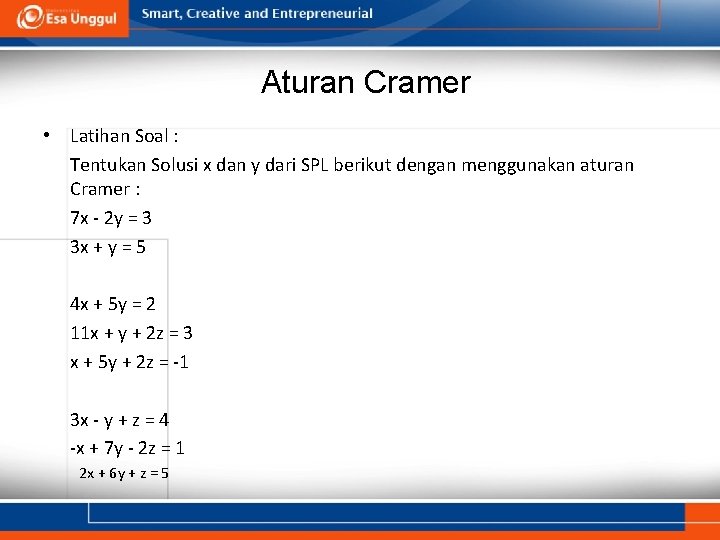
Aturan Cramer • Latihan Soal : Tentukan Solusi x dan y dari SPL berikut dengan menggunakan aturan Cramer : 7 x - 2 y = 3 3 x + y = 5 4 x + 5 y = 2 11 x + y + 2 z = 3 x + 5 y + 2 z = -1 3 x - y + z = 4 -x + 7 y - 2 z = 1 2 x + 6 y + z = 5

Kombinasi Linier • Misalkan kita memiliki suatu sistem persamaan linier (SPL) dengan satu, dua atau tiga variabel (x 1, x 2, x 3) atau kita dapat tuliskan dengan (x, y, z), maka dapat kita tuliskan sebagai Ax = b :

+ = • maka, dapat kita tuliskan menjadi : + = = sehingga kita dapat menuliskan hasil kombinasi linier SPL menjadi bentuk vektor kolom. + =

x Kombinasi Linier Lanjutan - 3 • Contoh : 1. tentukan kombinasi linier pada perkalian matriks : =

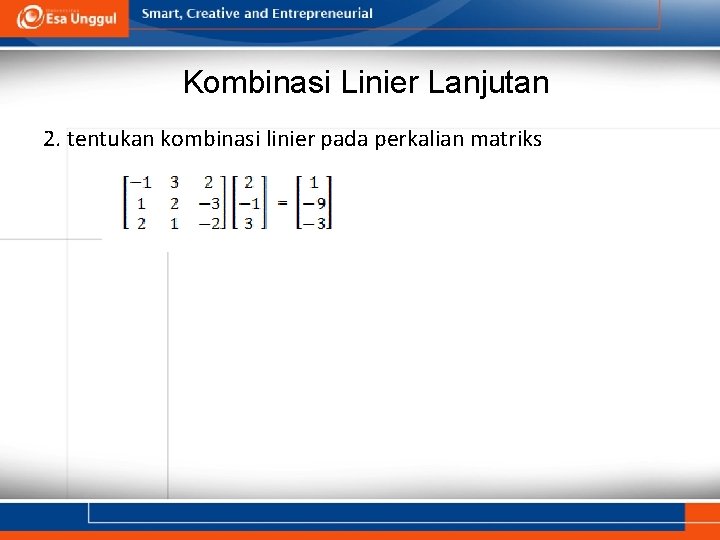
Kombinasi Linier Lanjutan 2. tentukan kombinasi linier pada perkalian matriks

Latihan Soal Kombinasi Linier • Tentukan matriks kolom AB sebagai kombinasi linier dari kolom matriks A • Tentukan matriks kolom BA sebagai kombinasi linier dari kolom matriks B

What’s next ? ? ? ? • Rank pada matriks, Ruang Vektor dan Ruang Inner Product • Baca Buku Kreyszig, E. Advanced Engineering Mathematics 9 th. (Ohio : Jhon Wiley & Sons, Inc, ) Chap. 7 • Sampai Ketemu Pekan depan