DETERMINAN Widita Kurniasari Universitas Trunojoyo Pengertian Determinan Determinan






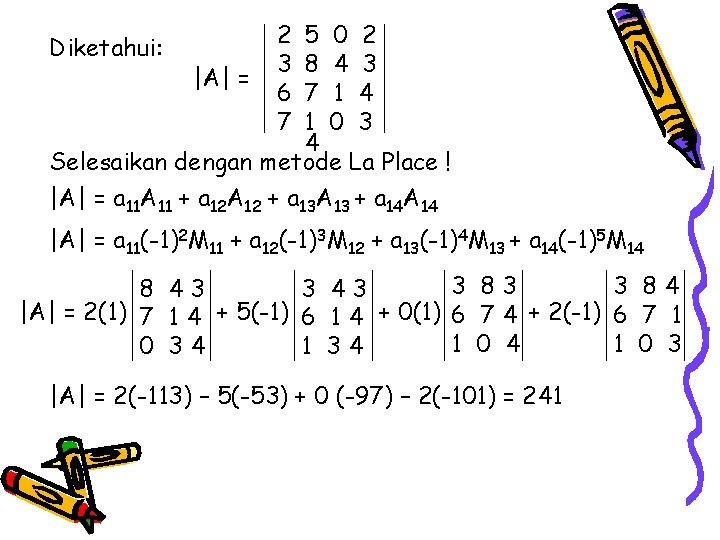

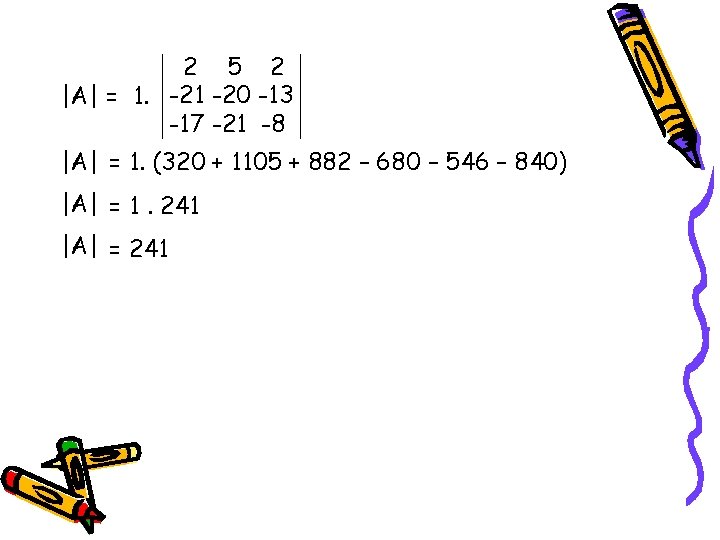

- Slides: 14

DETERMINAN Widita Kurniasari Universitas Trunojoyo

Pengertian Determinan • Determinan : nilai yang diperoleh dari matriks bujur sangkar, nilainya bisa + (positif), 0 (nol), - (negatif) • Determinan dari matriks A dinyatakan dengan |A|

Perhitungan Determinan • Matriks 2 x 2 A= 4 5 5 2 1 • Matriks 3 x 3 A= 2 5 0 3 8 4 4 6 7 1 |A| = 4 5 5 2 1 = (4 x 1) – (2 x 5) = -6 2 5 0 2 5 |A| = 3 8 4 6 7 4 6 1 7 |A| = (2 x 8 x 1 + 5 x 4 x 6 + 0 x 3 x 7) – (6 x 8 x 0 + 7 x 4 x 2 + 1 x 3 x 5) |A| = 136 -71 |A| = 65

Penyelesaian Determinan (La Place) a 11 a 12 a 13 |A| = a 21 a 22 a 23 a 31 a 32 a 33 |A| = a 11 a 22 a 23 a 32 a 33 M 11 - a 12 a 21 a 23 a 31 a 33 M 12 + a 13 a 21 a 22 a 31 a 32 M 13 Mij : minor dari unsur aij yang diperoleh dengan cara menutup baris ke i dan kolom ke j dari determinan |A|

Lanjutan cara La Place… Dalam notasi kofaktor menjadi : |A| = a 11 A 11 + a 12 A 12 + a 13 A 13 ………. Dimana: Aij = (-1)i+j Mij Penyelesaian dalam notasi minor : |A| = a 11 M 11 – a 12 M 12 + a 13 M 13 ……… Cara penyelesaian La Place berlaku untuk determinan berdimensi berapapun

Contoh Soal : 2 5 0 |A| = 3 8 4 4 6 7 1 8 4 3 4 |A| = 2 -5 7 1 6 1 + 0 |A| = 2 (-20) – 5 (-21) + 0 (-27) |A| = -40 + 105 + 0 |A| = 65 2 |A| = 3 6 7 5 0 2 8 4 3 7 1 4 1 0 3 4 3 8 6 7
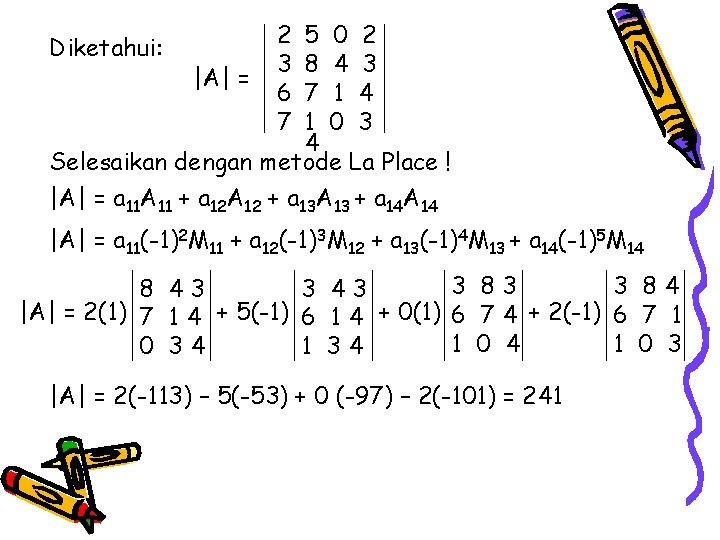
2 3 6 7 5 0 2 Diketahui: 8 4 3 |A| = 7 1 4 1 0 3 4 Selesaikan dengan metode La Place ! |A| = a 11 A 11 + a 12 A 12 + a 13 A 13 + a 14 A 14 |A| = a 11(-1)2 M 11 + a 12(-1)3 M 12 + a 13(-1)4 M 13 + a 14(-1)5 M 14 3 83 3 84 8 43 3 43 |A| = 2(1) 7 1 4 + 5(-1) 6 1 4 + 0(1) 6 7 4 + 2(-1) 6 7 1 1 0 4 1 0 34 1 34 |A| = 2(-113) – 5(-53) + 0 (-97) – 2(-101) = 241

Cara 2 (La Place) 5 0 2 8 4 3 Mengubah elemen a 23 = 4 dan 7 1 4 a 43 = 3 menjadi nol 1 0 3 4 Caranya : - semua elemen baris kedua dikurangi 4 x elemen baris ketiga - semua elemen baris keempat dikurangi 3 x elemen baris ketiga 2 |A| = 3 6 7 2 5 |A| = -21 -20 6 7 -17 -21 0 2 0 -13 = a 13 A 13 + a 23 A 23 + a 33 A 33 + a 43 A 43 1 4 0 0 -8 |A| = a 33. A 33 = 1. (-1)3+3. |M 33| |A| = 1. |M 33|
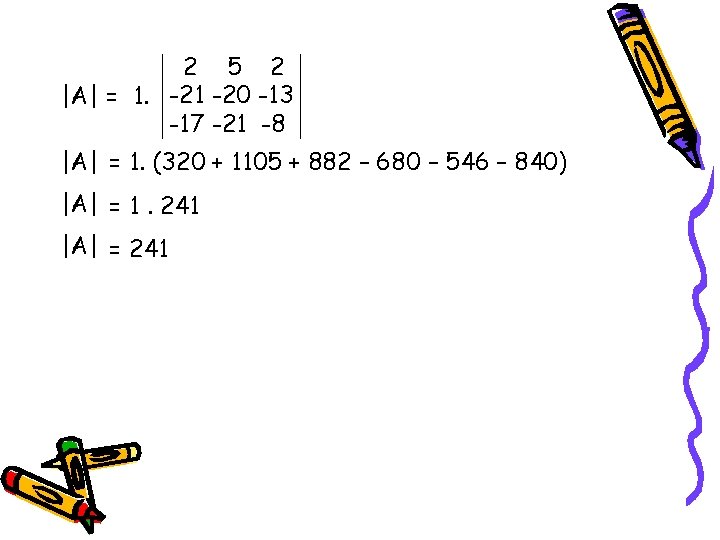
2 5 2 |A| = 1. -21 -20 -13 -17 -21 -8 |A| = 1. (320 + 1105 + 882 – 680 – 546 – 840) |A| = 1. 241 |A| = 241

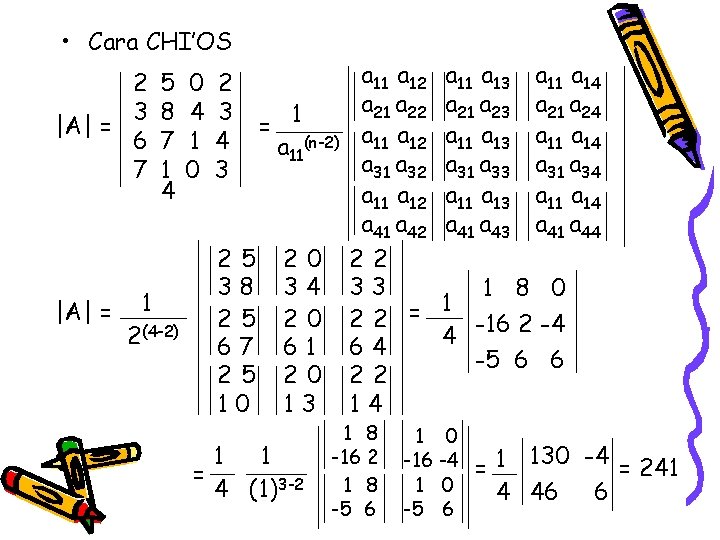
• Cara CHI’OS 2 3 |A| = 6 7 5 8 7 1 4 |A| = 1 2(4 -2) 0 4 1 0 2 3 4 3 25 38 25 67 25 10 = 1 a 11(n-2) 20 34 20 61 20 13 1 1 = 4 (1)3 -2 a 11 a 12 a 21 a 22 a 11 a 12 a 31 a 32 a 11 a 12 a 41 a 42 22 33 22 = 64 22 14 1 8 -16 2 1 8 -5 6 a 11 a 13 a 21 a 23 a 11 a 13 a 31 a 33 a 11 a 13 a 41 a 43 a 11 a 14 a 21 a 24 a 11 a 14 a 31 a 34 a 11 a 14 a 41 a 44 1 8 0 1 4 -16 2 -4 -5 6 6 1 0 -16 -4 1 0 -5 6 = 1 130 -4 = 241 4 46 6

Sifat-sifat Determinan 1. Nilai determinan adalah nol jika semua unsurnya sama. 2 2 2 |A| = 2 2 2 = 8 + 8 – 8 – 8 = 0 2 2. Nilai determinan adalah nol jika terdapat dua baris atau dua kolom yang unsur-unsurnya sama 2 6 5 |A| = 1 8 4 = 80 + 48 + 30 – 80 – 30 – 48 = 0 2 6 5

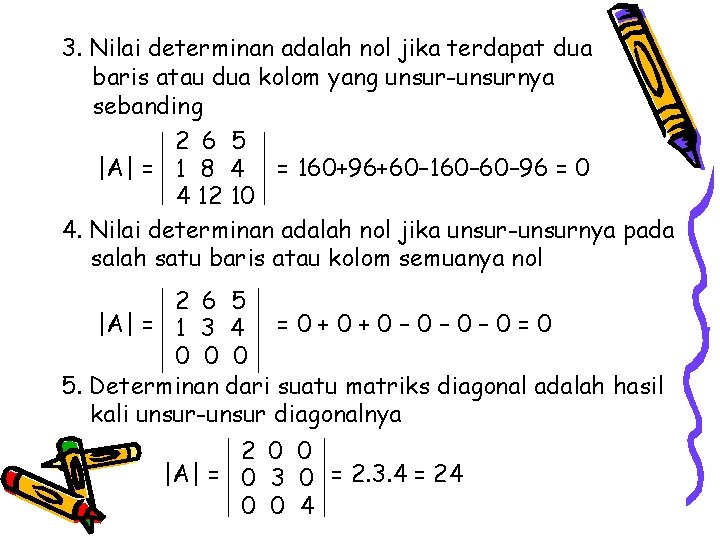
3. Nilai determinan adalah nol jika terdapat dua baris atau dua kolom yang unsur-unsurnya sebanding 2 6 5 |A| = 1 8 4 = 160+96+60– 160– 96 = 0 4 12 10 4. Nilai determinan adalah nol jika unsur-unsurnya pada salah satu baris atau kolom semuanya nol 2 6 5 |A| = 1 3 4 = 0 + 0 – 0 – 0 = 0 0 5. Determinan dari suatu matriks diagonal adalah hasil kali unsur-unsur diagonalnya 2 0 0 |A| = 0 3 0 = 2. 3. 4 = 24 0 0 4

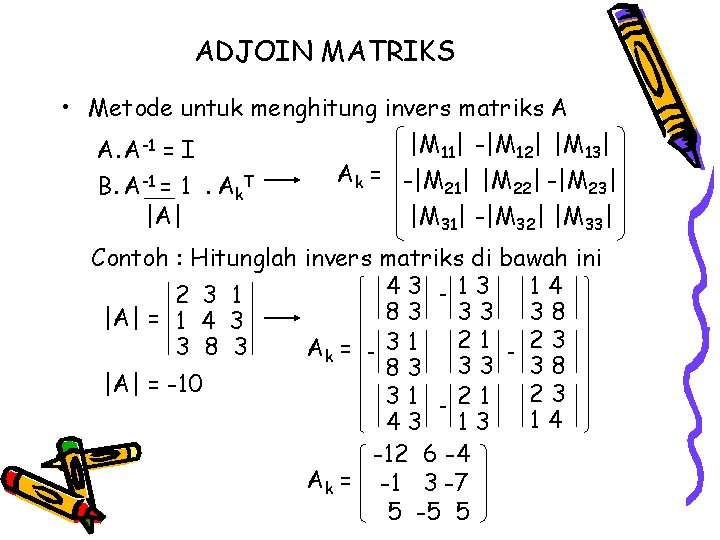
ADJOIN MATRIKS • Metode untuk menghitung invers matriks A |M 11| -|M 12| |M 13| A. A-1 = I Ak = -|M 21| |M 22| -|M 23| B. A-1 = 1. Ak. T |A| |M 31| -|M 32| |M 33| Contoh : Hitunglah invers matriks di bawah ini 43 - 13 14 2 3 1 83 33 38 |A| = 1 4 3 21 - 23 3 8 3 Ak = - 3 1 83 33 38 |A| = -10 23 31 - 21 14 43 13 -12 6 -4 Ak = -1 3 -7 5 -5 5

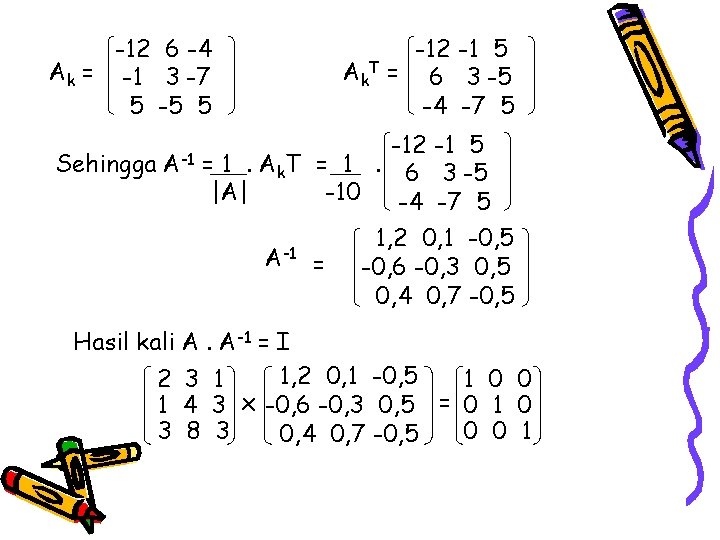
-12 6 -4 Ak = -1 3 -7 5 -5 5 Sehingga A-1 -12 -1 5 Ak. T = 6 3 -5 -4 -7 5 -12 -1 5 = 1. Ak. T = 1. 6 3 -5 |A| -10 -4 -7 5 1, 2 0, 1 -0, 5 -1 A = -0, 6 -0, 3 0, 5 0, 4 0, 7 -0, 5 Hasil kali A. A-1 = I 1, 2 0, 1 -0, 5 2 3 1 1 0 0 1 4 3 x -0, 6 -0, 3 0, 5 = 0 1 0 3 8 3 0 0 1 0, 4 0, 7 -0, 5
 Bakso arief trunojoyo bandung
Bakso arief trunojoyo bandung Dr ratna kurniasari
Dr ratna kurniasari Soal latihan determinan
Soal latihan determinan Menghilangkan
Menghilangkan Sifat sifat determinan matriks ordo 2x2
Sifat sifat determinan matriks ordo 2x2 1/ad-bc
1/ad-bc Notasi determinan matriks
Notasi determinan matriks Nilai determinan matriks
Nilai determinan matriks Universitas debreceniensis
Universitas debreceniensis Kepemimpinan iowa
Kepemimpinan iowa Sekjur psikologi gunadarma
Sekjur psikologi gunadarma Remunerasi blu universitas
Remunerasi blu universitas Biaya masuk universitas muhammadiyah tangerang
Biaya masuk universitas muhammadiyah tangerang Luas universitas mataram
Luas universitas mataram Lsp universitas gunadarma
Lsp universitas gunadarma



























