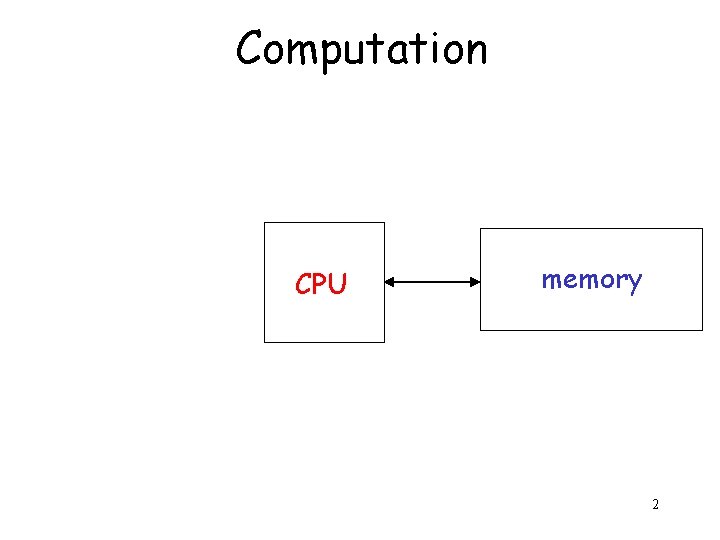
CSCI2400 Models of Computation 1 Computation CPU memory









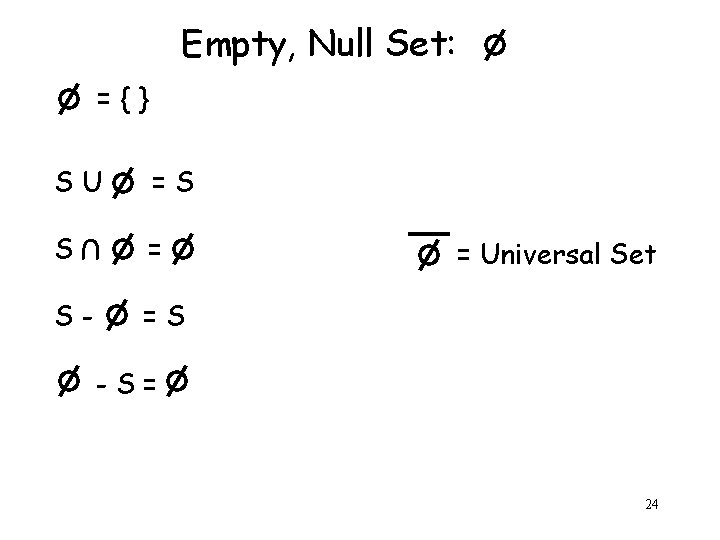














- Slides: 58

CSCI-2400 Models of Computation 1

Computation CPU memory 2

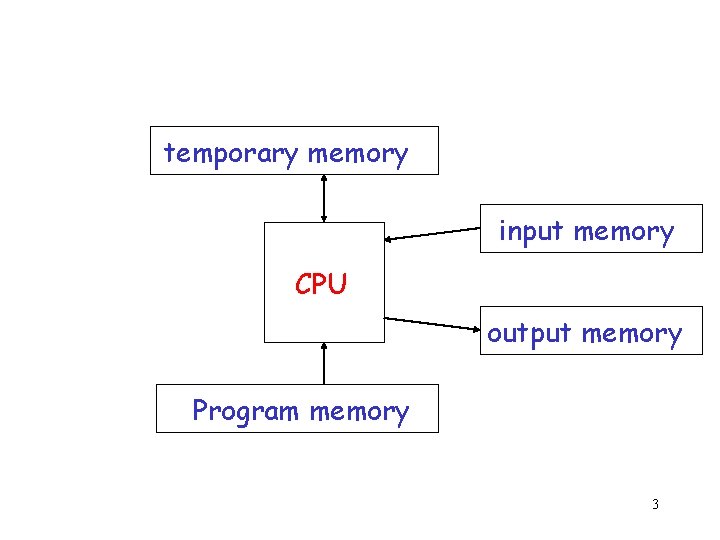
temporary memory input memory CPU output memory Program memory 3

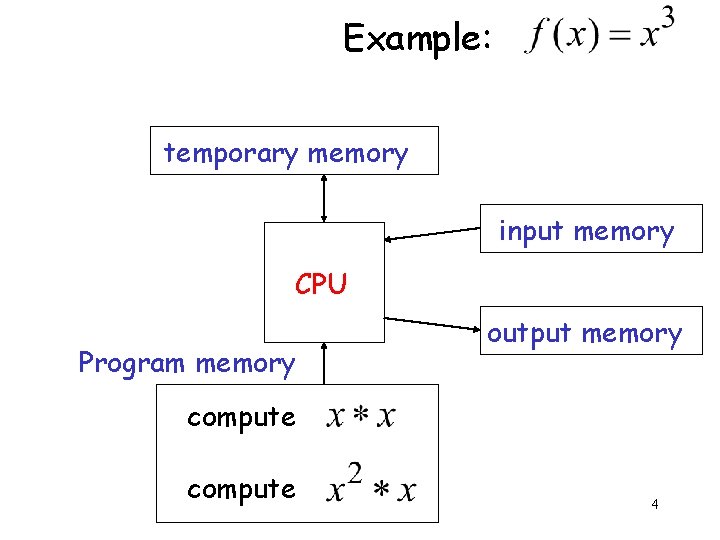
Example: temporary memory input memory CPU Program memory output memory compute 4

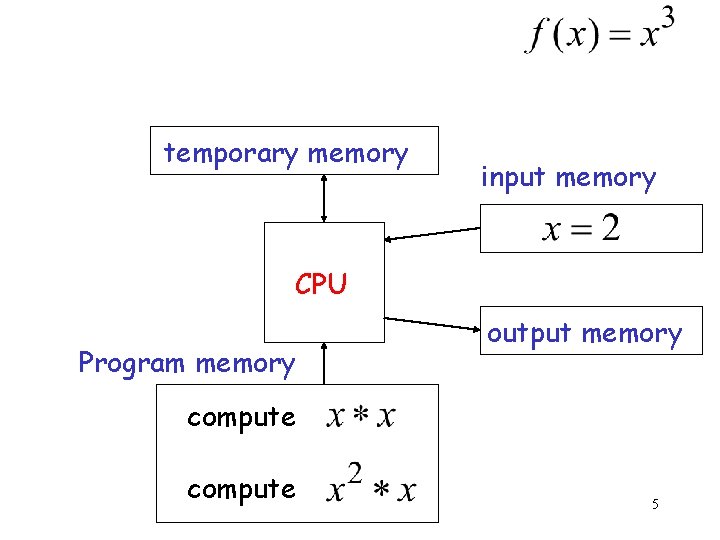
temporary memory input memory CPU Program memory output memory compute 5

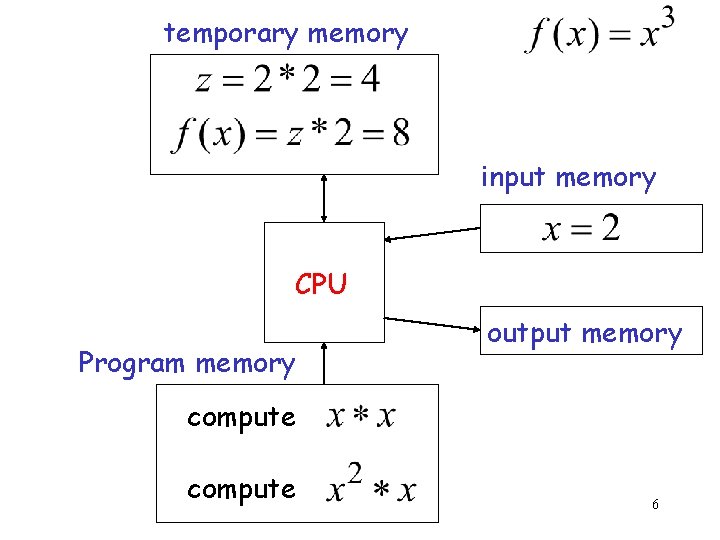
temporary memory input memory CPU Program memory output memory compute 6

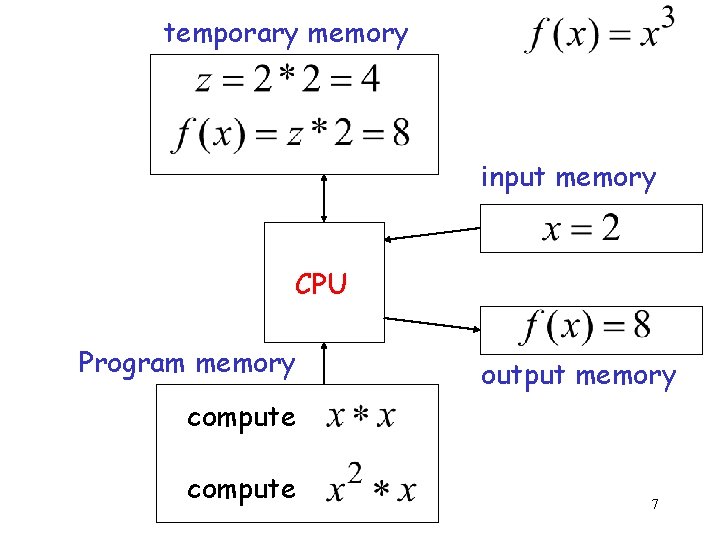
temporary memory input memory CPU Program memory output memory compute 7

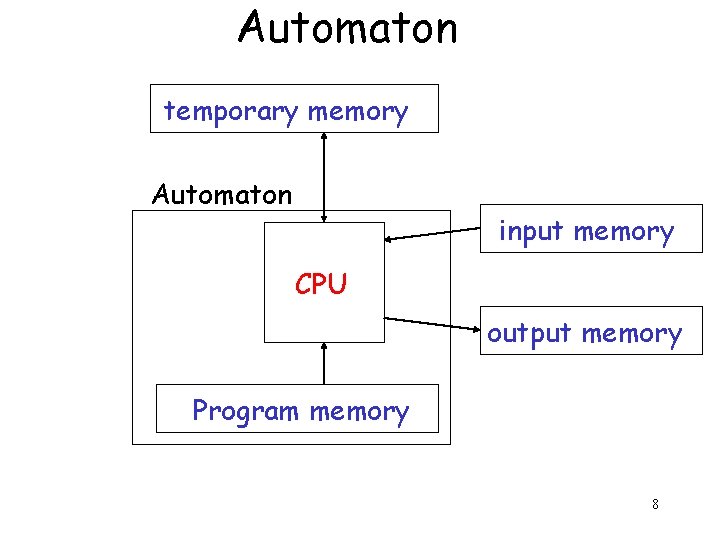
Automaton temporary memory Automaton input memory CPU output memory Program memory 8

Different Kinds of Automata are distinguished by the temporary memory • Finite Automata: no temporary memory • Pushdown Automata: stack • Turing Machines: random access memory 9

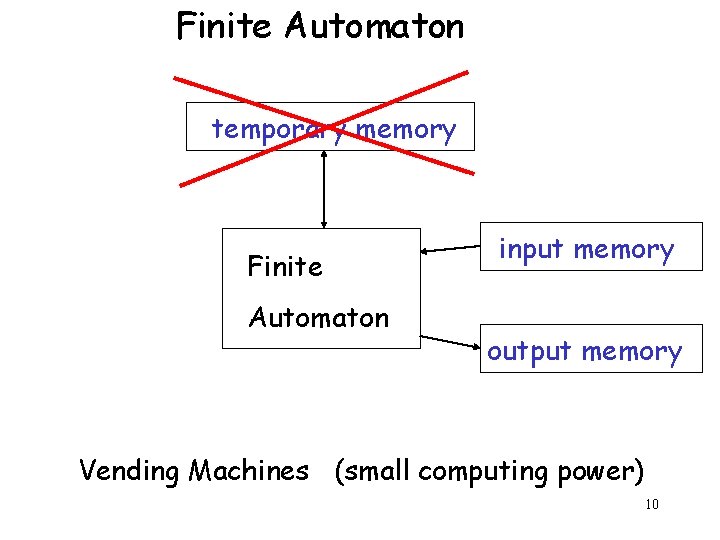
Finite Automaton temporary memory Finite Automaton input memory output memory Vending Machines (small computing power) 10

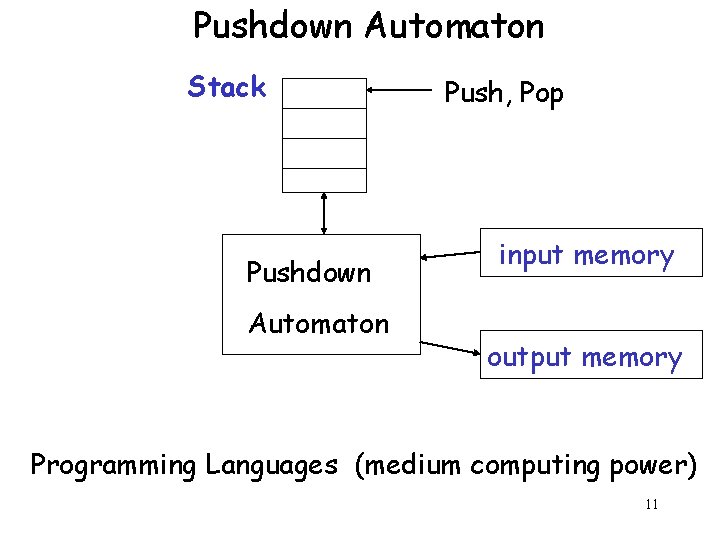
Pushdown Automaton Stack Pushdown Automaton Push, Pop input memory output memory Programming Languages (medium computing power) 11

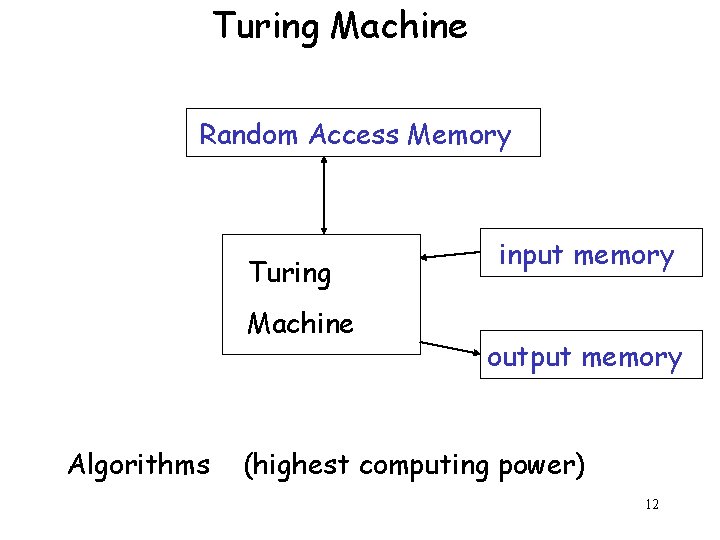
Turing Machine Random Access Memory Turing Machine Algorithms input memory output memory (highest computing power) 12

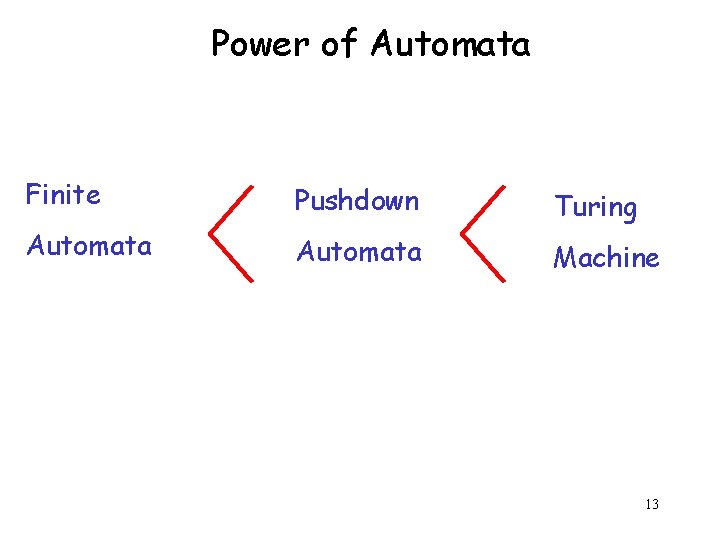
Power of Automata Finite Pushdown Automata Turing Automata Machine 13

We will show later in class • How to build compilers for programming languages • Some computational problems cannot be solved • Some problems are hard to solve 14

Mathematical Preliminaries 15

Mathematical Preliminaries • Sets • Functions • Relations • Graphs • Proof Techniques 16

SETS A set is a collection of elements We write 17

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } 18

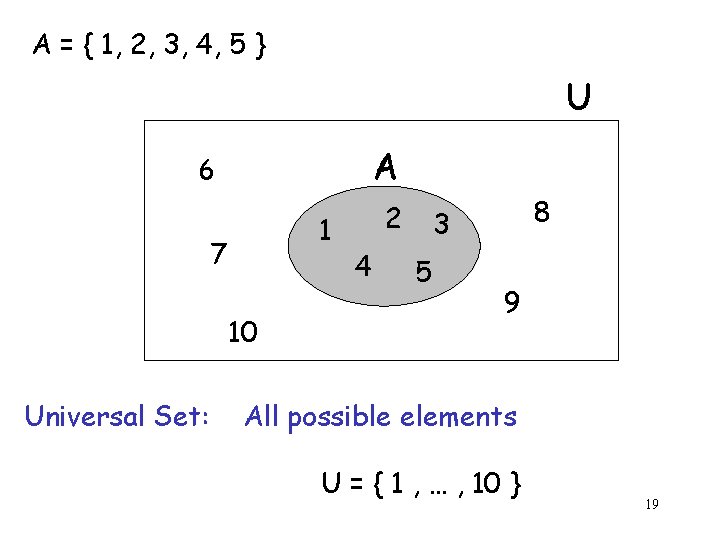
A = { 1, 2, 3, 4, 5 } U A 6 1 7 10 Universal Set: 2 4 8 3 5 9 All possible elements U = { 1 , … , 10 } 19

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} A • Union B A U B = { 1, 2, 3, 4, 5 } • Intersection U A B = { 2, 3 } • Difference A-B={1} B - A = { 4, 5 } A-B 20

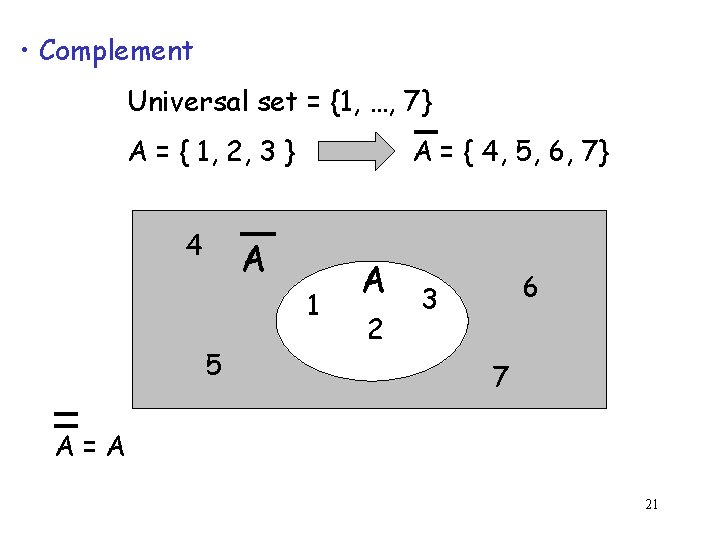
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A 21

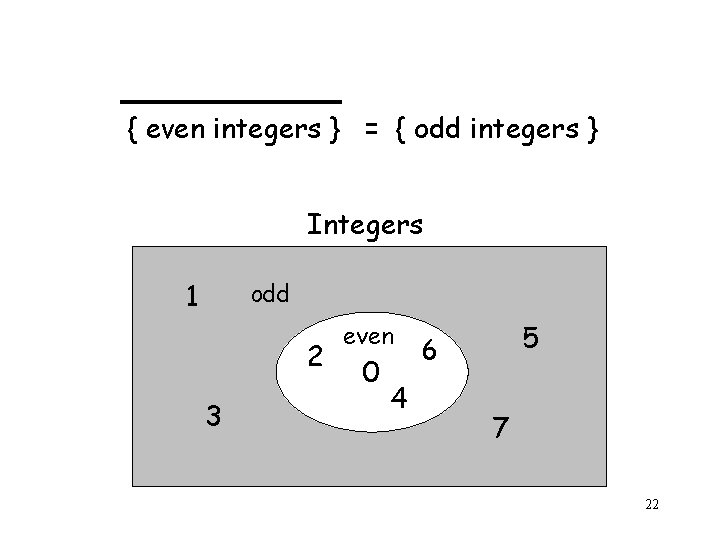
{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 22

De. Morgan’s Laws U AUB=A B B=AUB 23
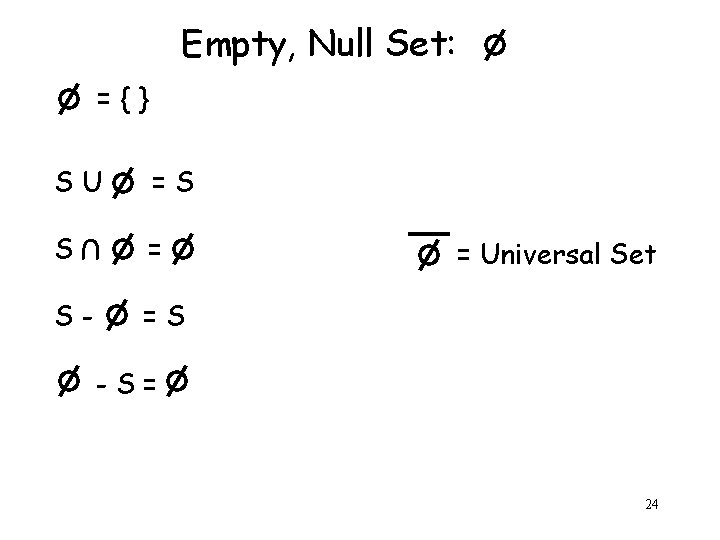
Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= 24

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A 25

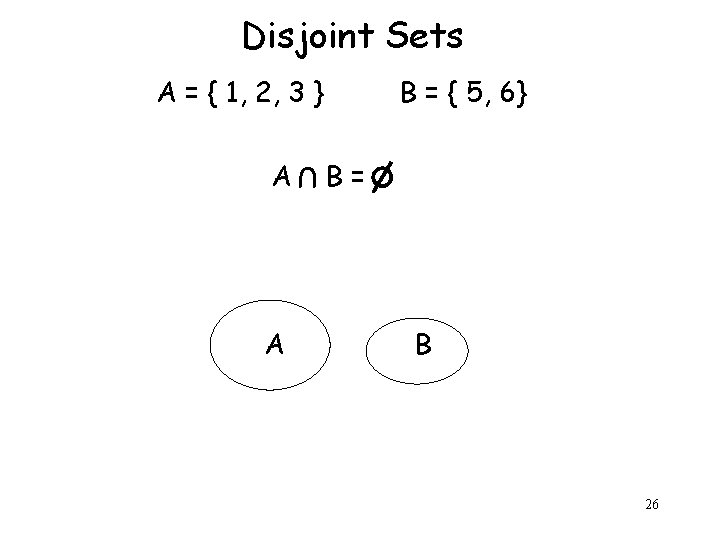
Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B 26

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 27

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 28

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 4) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ 29

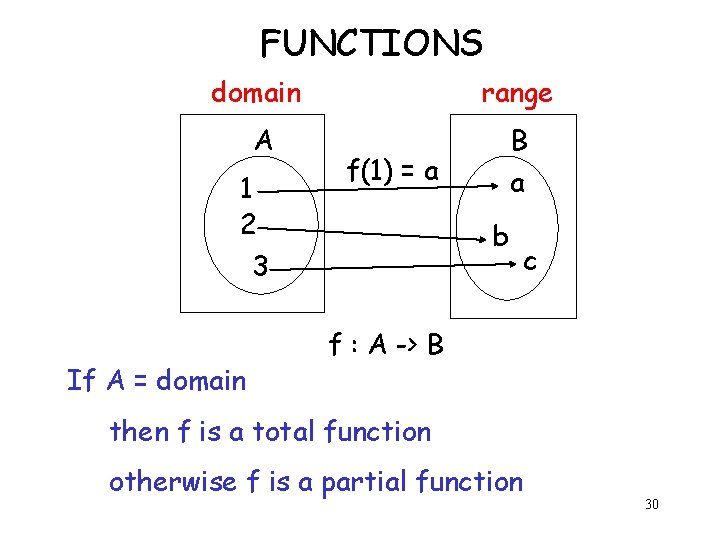
FUNCTIONS domain range A B 1 2 3 If A = domain f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function 30

RELATIONS R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} x i R yi e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 In relations xi can be repeated 31

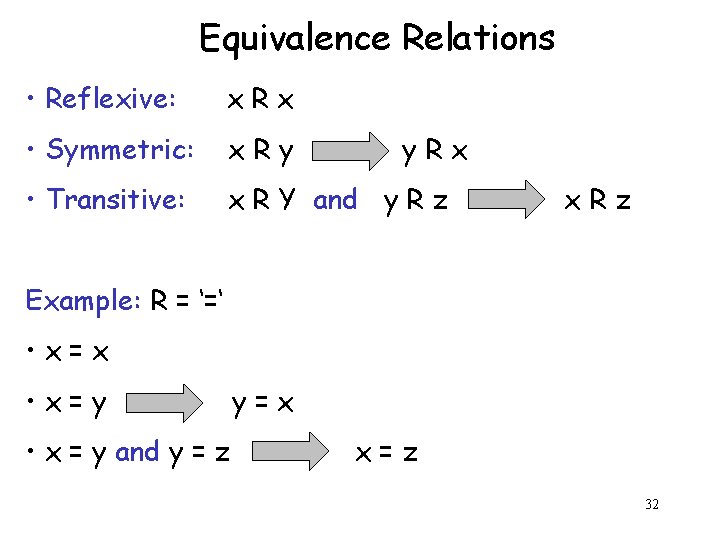
Equivalence Relations • Reflexive: x. Rx • Symmetric: x. Ry • Transitive: x R Y and y R z y. Rx x. Rz Example: R = ‘=‘ • x=x • x=y • x = y and y = z y=x x=z 32

Equivalence Classes For equivalence relation R equivalence class of x = {y : x R y} Example: R = { (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (4, 4), (3, 4), (4, 3) } Equivalence class of 1 = {1, 2} Equivalence class of 3 = {3, 4} 33

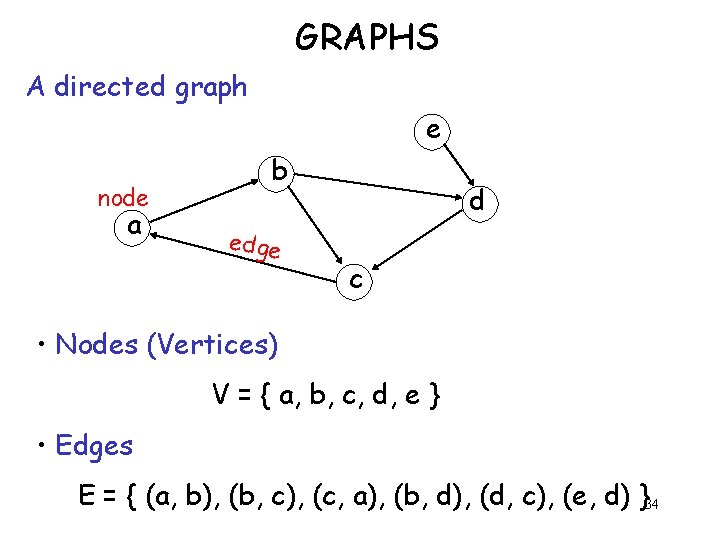
GRAPHS A directed graph e node a b edge d c • Nodes (Vertices) V = { a, b, c, d, e } • Edges E = { (a, b), (b, c), (c, a), (b, d), (d, c), (e, d) }34

Labeled Graph 6 a b 1 5 3 e 6 2 d c 35

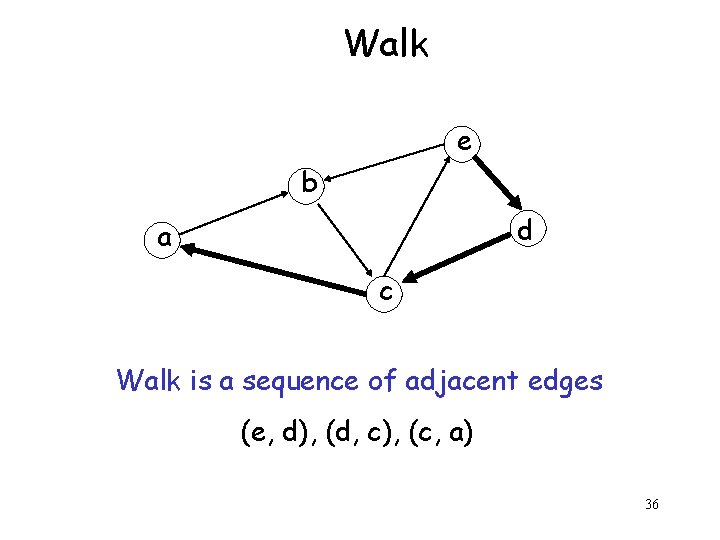
Walk e b d a c Walk is a sequence of adjacent edges (e, d), (d, c), (c, a) 36

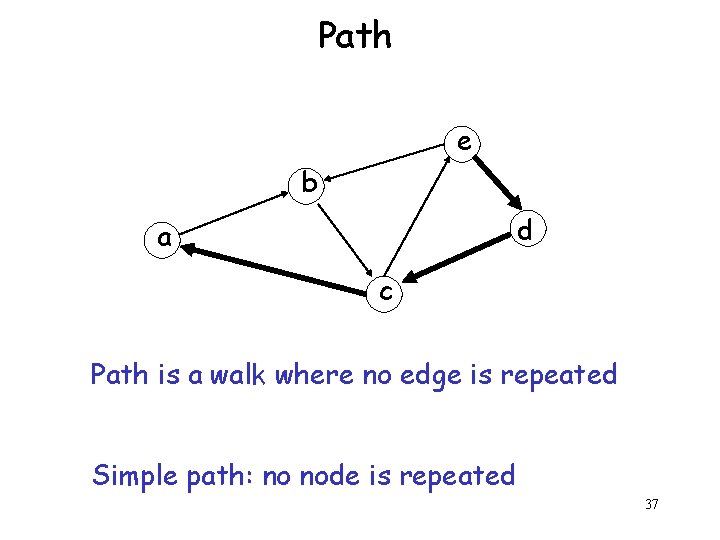
Path e b d a c Path is a walk where no edge is repeated Simple path: no node is repeated 37

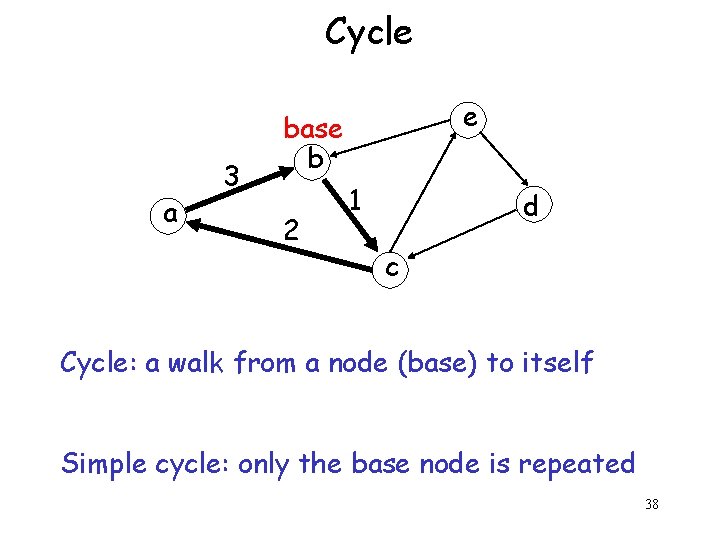
Cycle a 3 e base b 2 1 d c Cycle: a walk from a node (base) to itself Simple cycle: only the base node is repeated 38

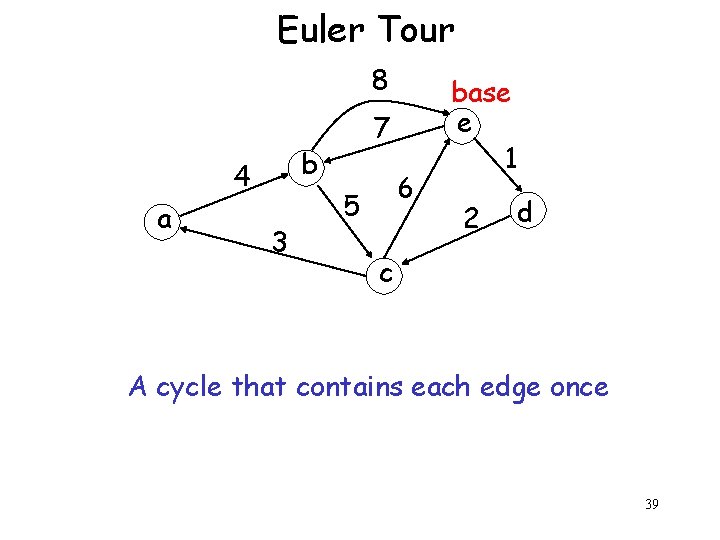
Euler Tour 8 b 4 a 7 3 6 5 base e 1 2 d c A cycle that contains each edge once 39

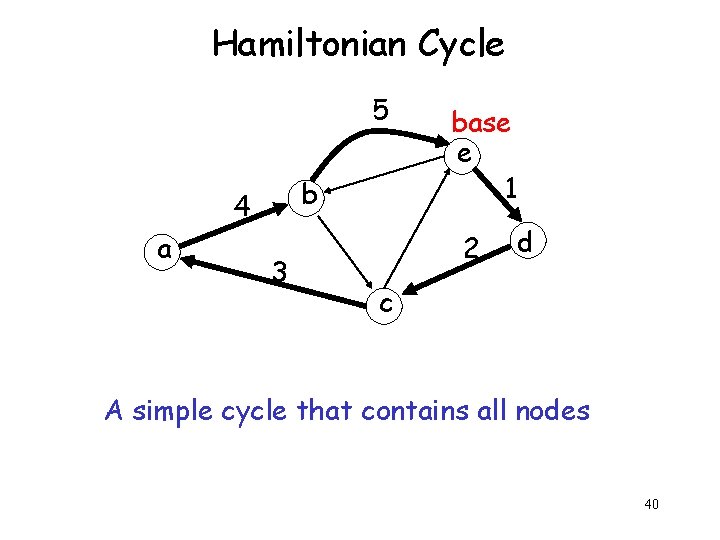
Hamiltonian Cycle 5 b 4 a 3 base e 1 2 d c A simple cycle that contains all nodes 40

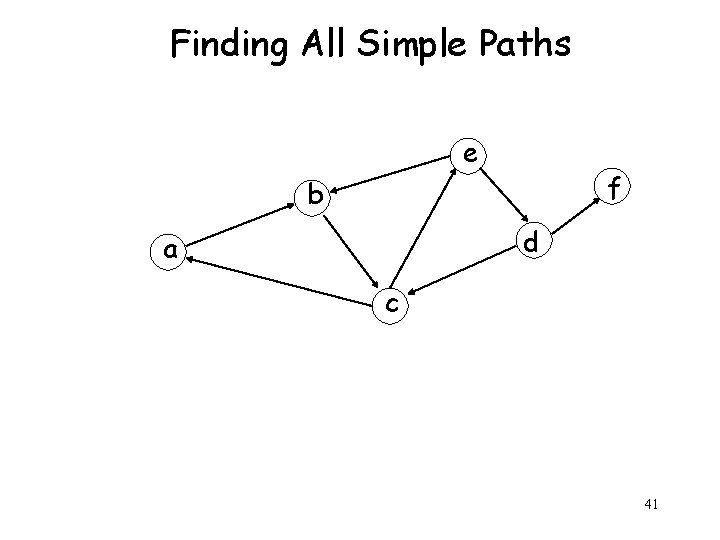
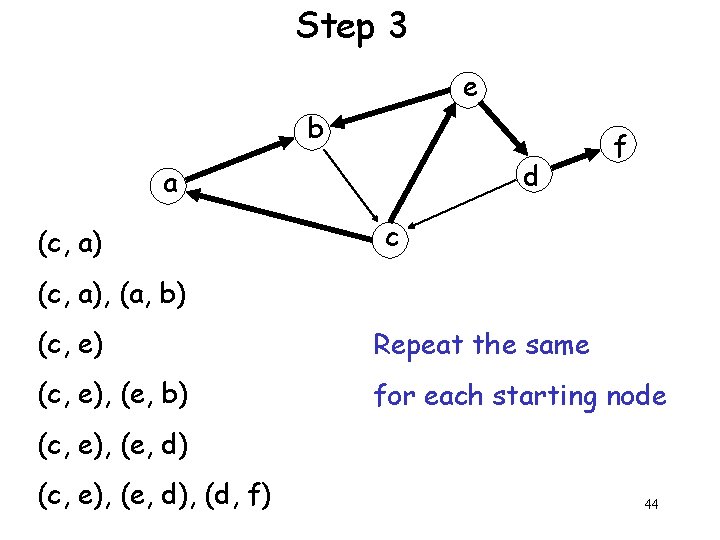
Finding All Simple Paths e f b d a c 41

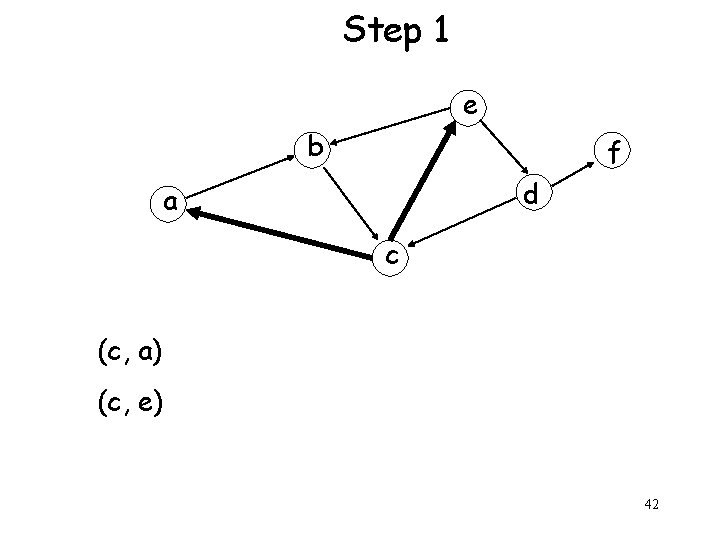
Step 1 e b f d a c (c, a) (c, e) 42

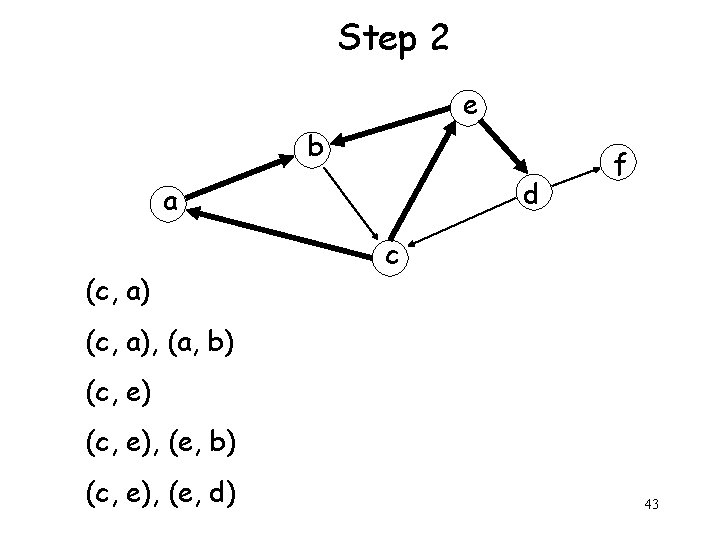
Step 2 e b d a (c, a) f c (c, a), (a, b) (c, e), (e, d) 43

Step 3 e b d a (c, a) f c (c, a), (a, b) (c, e) Repeat the same (c, e), (e, b) for each starting node (c, e), (e, d), (d, f) 44

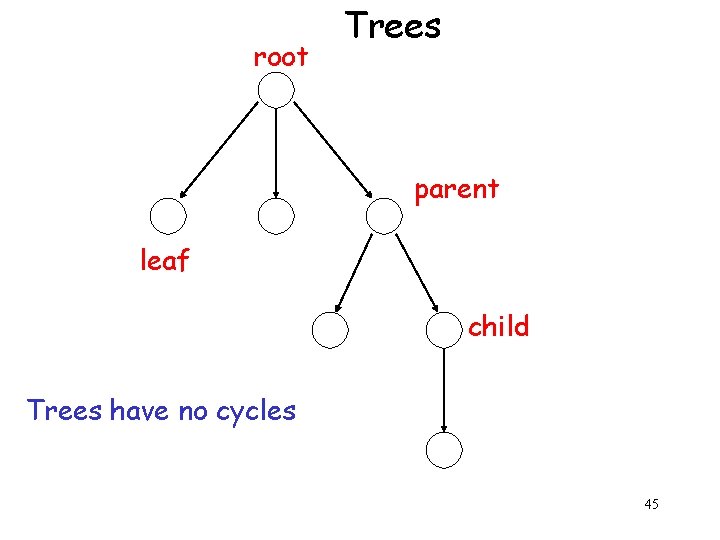
root Trees parent leaf child Trees have no cycles 45

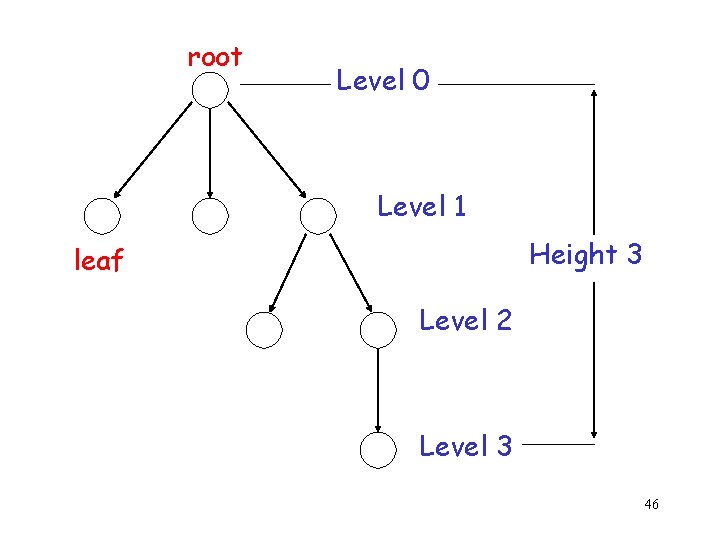
root Level 0 Level 1 Height 3 leaf Level 2 Level 3 46

Binary Trees 47

PROOF TECHNIQUES • Proof by induction • Proof by contradiction 48

Induction We have statements P 1, P 2, P 3, … If we know • for some k that P 1, P 2, …, Pk are true • for any n >= k that P 1, P 2, …, Pn imply Pn+1 Then Every Pi is true 49

Proof by Induction • Inductive basis Find P 1, P 2, …, Pk which are true • Inductive hypothesis Let’s assume P 1, P 2, …, Pn are true, for any n >= k • Inductive step Show that Pn+1 is true 50

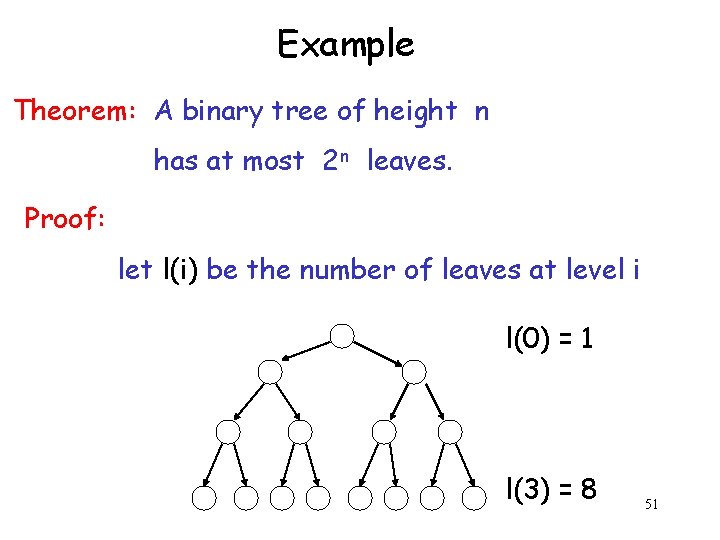
Example Theorem: A binary tree of height n has at most 2 n leaves. Proof: let l(i) be the number of leaves at level i l(0) = 1 l(3) = 8 51

We want to show: l(i) <= 2 i • Inductive basis l(0) = 1 (the root node) • Inductive hypothesis Let’s assume l(i) <= 2 i for all i = 0, 1, …, n • Induction step we need to show that l(n + 1) <= 2 n+1 52

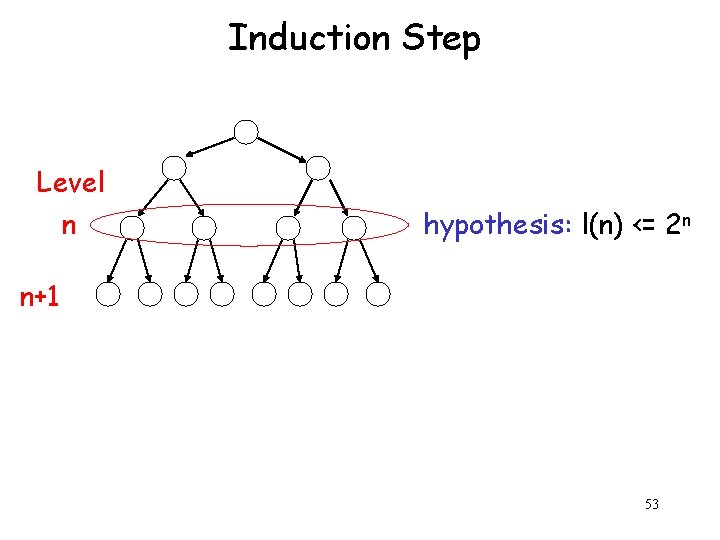
Induction Step Level n hypothesis: l(n) <= 2 n n+1 53

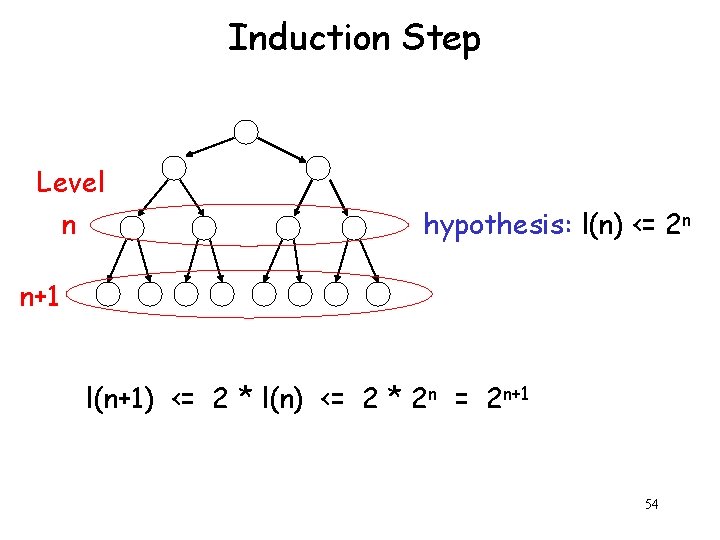
Induction Step Level n hypothesis: l(n) <= 2 n n+1 l(n+1) <= 2 * l(n) <= 2 * 2 n = 2 n+1 54

Remark Recursion is another thing Example of recursive function: f(n) = f(n-1) + f(n-2) f(0) = 1, f(1) = 1 55

Proof by Contradiction We want to prove that a statement P is true • we assume that P is false • then we arrive at an incorrect conclusion • therefore, statement P must be true 56

Example Theorem: is not rational Proof: Assume by contradiction that it is rational = n/m n and m have no common factors We will show that this is impossible 57

= n/m Therefore, 2 m 2 = 4 k 2 n 2 2 m 2 = n 2 is even m 2 = 2 k 2 n is even n=2 k m is even m=2 p Thus, m and n have common factor 2 Contradiction! 58