Control Systems CS Dr Imtiaz Hussain Associate Professor

Control Systems (CS) Dr. Imtiaz Hussain Associate Professor Mehran University of Engineering & Technology Jamshoro, Pakistan email: imtiaz. hussain@faculty. muet. edu. pk URL : http: //imtiazhussainkalwar. weebly. com/ 6 th Semester 14 ES (SEC-I) Note: I do not claim any originality in these lectures. The contents of this presentation are mostly taken from the book of Ogatta, Norman Nise, Bishop and B C. Kuo and various other 1 internet sources.

Outline • Introduction • Standard Test Signals • Transient Response of 1 st Order Systems • Transient Response of 2 nd Order Systems • S-Plane • Transient Response Specifications of 2 md order System • Examples

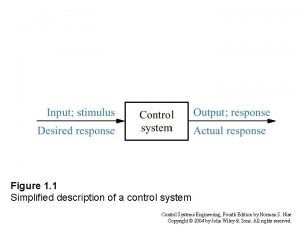
Introduction • In time-domain analysis the response of a dynamic system to an input is expressed as a function of time. • It is possible to compute the time response of a system if the nature of input and the mathematical model of the system are known. • Usually, the input signals to control systems are not known fully ahead of time. • For example, in a radar tracking system, the position and the speed of the target to be tracked may vary in a random fashion. • It is therefore difficult to express the actual input signals mathematically by simple equations.

Standard Test Signals • The characteristics of actual input signals are a sudden shock, a sudden change, a constant velocity, and constant acceleration. • The dynamic behavior of a system is therefore judged and compared under application of standard test signals – an impulse, a step, a constant velocity, and constant acceleration. • Another standard signal of great importance is a sinusoidal signal.

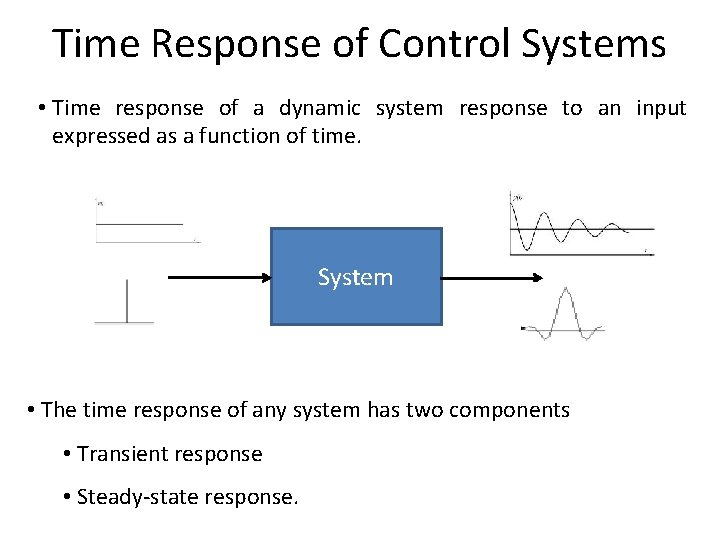
Time Response of Control Systems • Time response of a dynamic system response to an input expressed as a function of time. System • The time response of any system has two components • Transient response • Steady-state response.

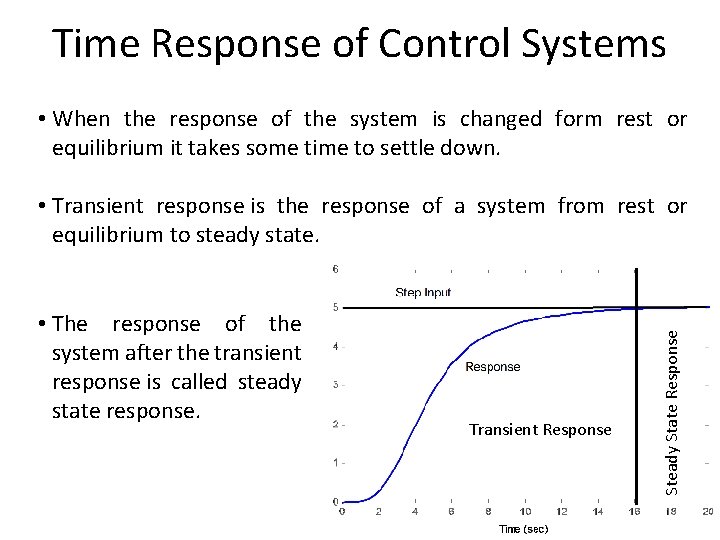
Time Response of Control Systems • When the response of the system is changed form rest or equilibrium it takes some time to settle down. • The response of the system after the transient response is called steady state response. Transient Response Steady State Response • Transient response is the response of a system from rest or equilibrium to steady state.

Time Response of Control Systems • Transient response depend upon the system poles only and not on the type of input. • It is therefore sufficient to analyze the transient response using a step input. • The steady-state response depends on system dynamics and the input quantity. • It is then examined using different test signals by final value theorem.

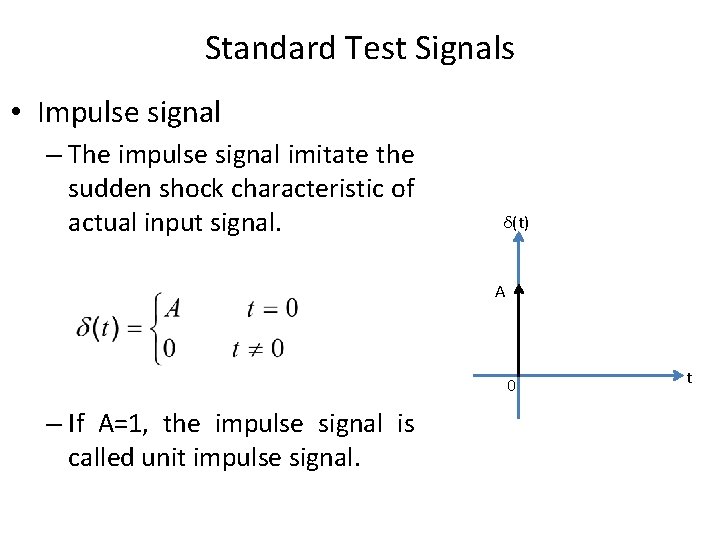
Standard Test Signals • Impulse signal – The impulse signal imitate the sudden shock characteristic of actual input signal. δ(t) A 0 – If A=1, the impulse signal is called unit impulse signal. t

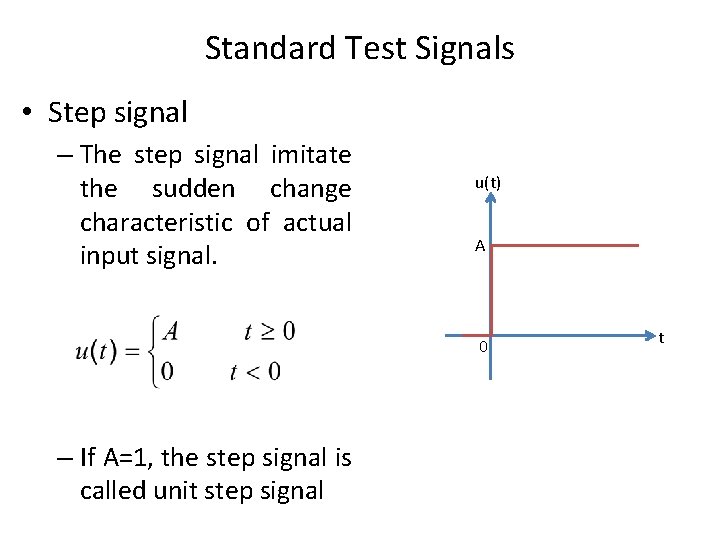
Standard Test Signals • Step signal – The step signal imitate the sudden change characteristic of actual input signal. u(t) A 0 – If A=1, the step signal is called unit step signal t

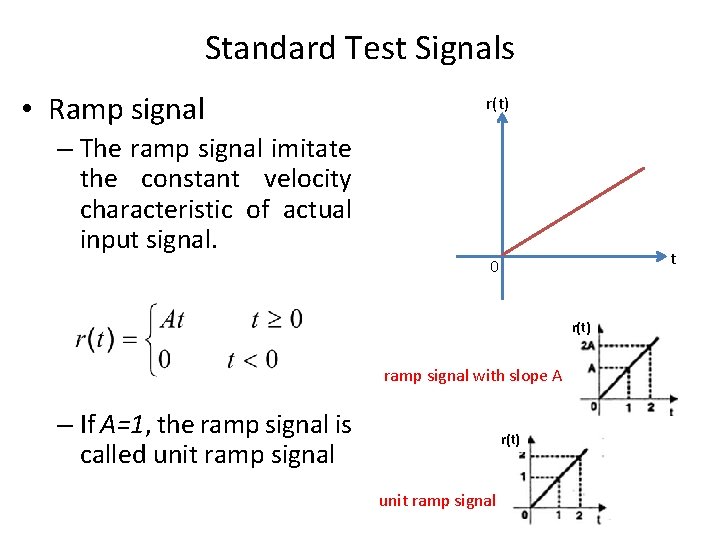
Standard Test Signals • Ramp signal – The ramp signal imitate the constant velocity characteristic of actual input signal. r(t) t 0 r(t) ramp signal with slope A – If A=1, the ramp signal is called unit ramp signal r(t) unit ramp signal

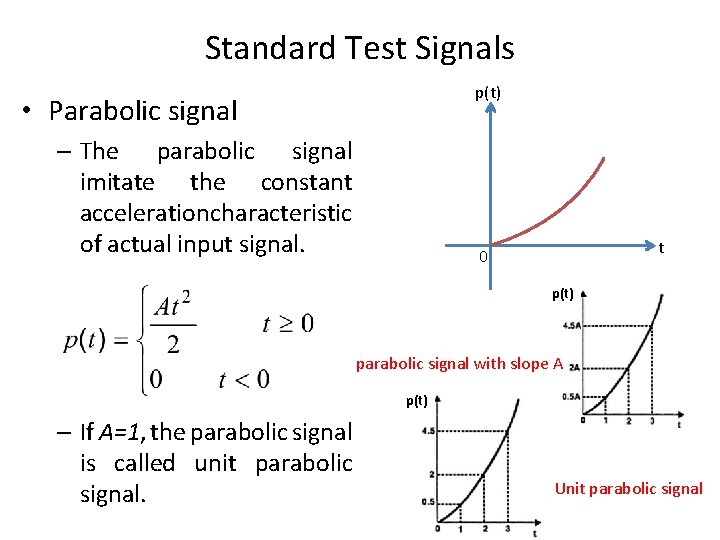
Standard Test Signals p(t) • Parabolic signal – The parabolic signal imitate the constant acceleration characteristic of actual input signal. t 0 p(t) parabolic signal with slope A p(t) – If A=1, the parabolic signal is called unit parabolic signal. Unit parabolic signal

Relation between standard Test Signals • Impulse • Step • Ramp • Parabolic

Laplace Transform of Test Signals • Impulse • Step

Laplace Transform of Test Signals • Ramp • Parabolic

First Oder System • The first order system has only one pole. • Where K is the D. C gain and T is the time constant of the system. • Time constant is a measure of how quickly a 1 st order system responds to a unit step input. • D. C Gain of the system is ratio between the input signal and the steady state value of output.

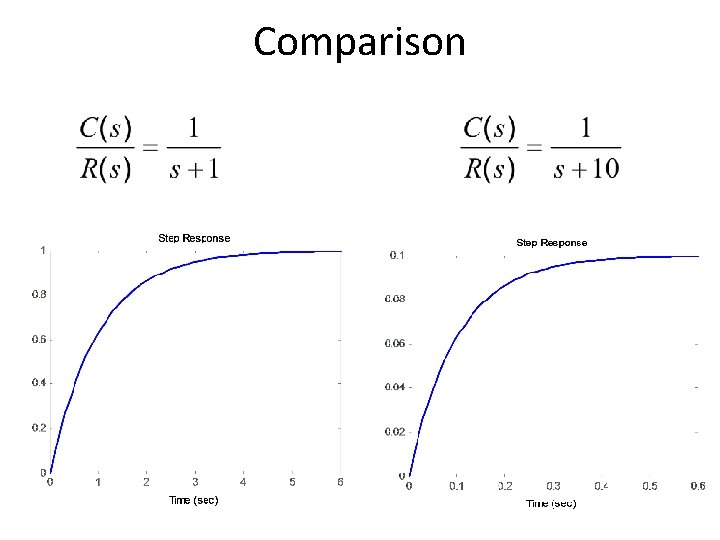
First Oder System • The first order system given below. • D. C gain is 10 and time constant is 3 seconds. • And for following system • D. C Gain of the system is 3/5 and time constant is 1/5 seconds.

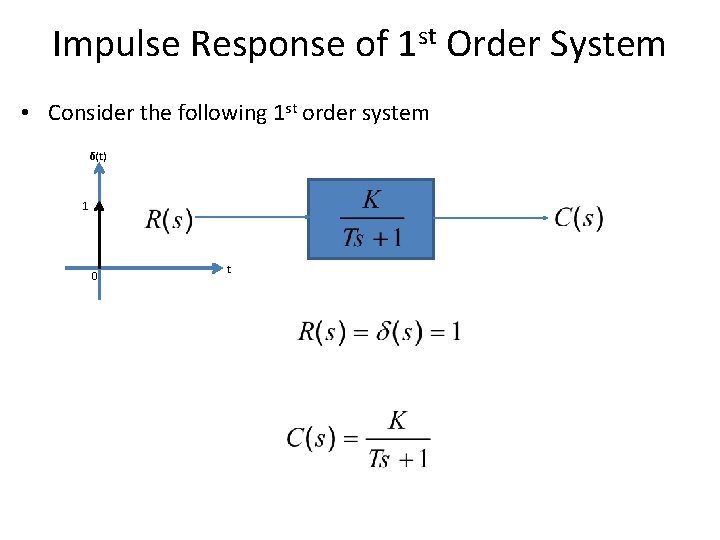
Impulse Response of 1 st Order System • Consider the following 1 st order system δ(t) 1 0 t

Impulse Response of 1 st Order System • Re-arrange above equation as • In order represent the response of the system in time domain we need to compute inverse Laplace transform of the above equation.

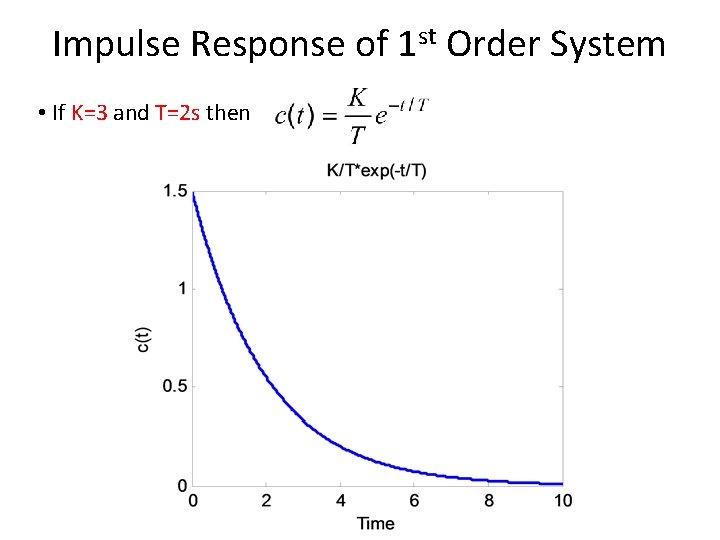
Impulse Response of 1 st Order System • If K=3 and T=2 s then

Step Response of 1 st Order System • Consider the following 1 st order system • In order to find out the inverse Laplace of the above equation, we need to break it into partial fraction expansion Forced Response Natural Response

Step Response of 1 st Order System • Taking Inverse Laplace of above equation • Where u(t)=1 • When t=T

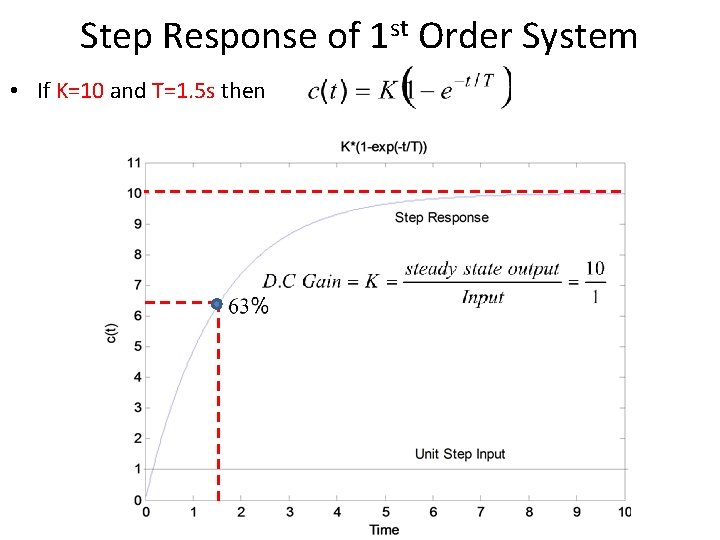
Step Response of 1 st Order System • If K=10 and T=1. 5 s then

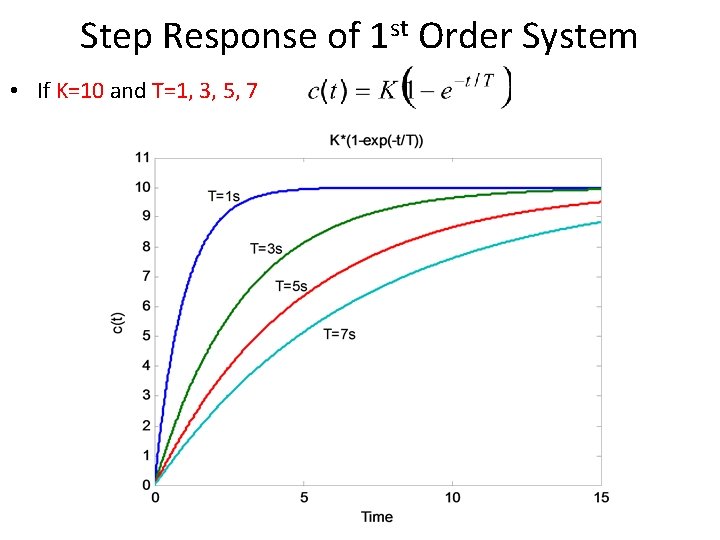
Step Response of 1 st Order System • If K=10 and T=1, 3, 5, 7

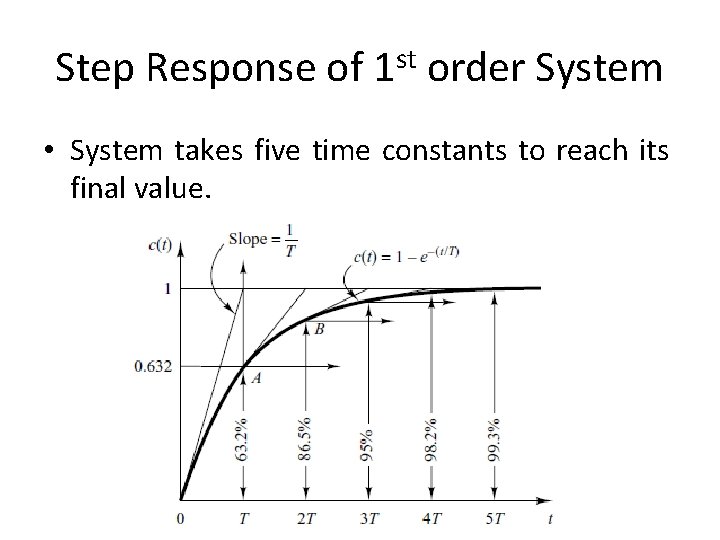
Step Response of 1 st order System • System takes five time constants to reach its final value.

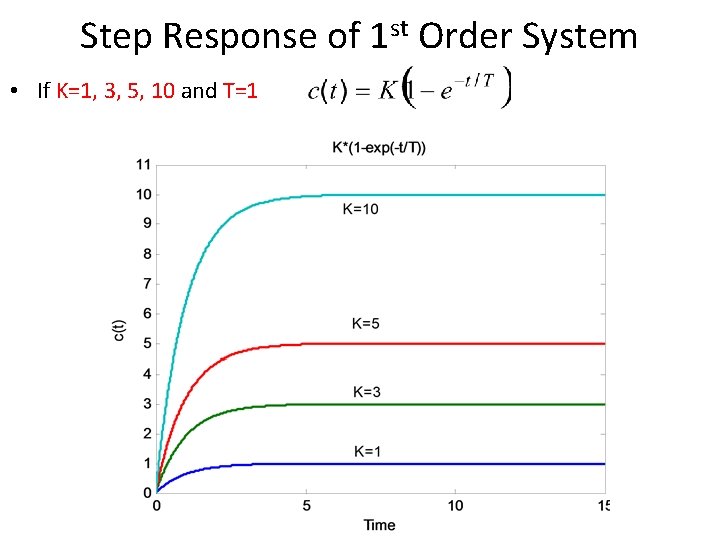
Step Response of 1 st Order System • If K=1, 3, 5, 10 and T=1

Relation Between Step and impulse response • The step response of the first order system is • Differentiating c(t) with respect to t yields

Example#1 • Impulse response of a 1 st order system is given below. • Find out – – Time constant T D. C Gain K Transfer Function Step Response

Example#1 • The Laplace Transform of Impulse response of a system is actually the transfer function of the system. • Therefore taking Laplace Transform of the impulse response given by following equation.

Example#1 • Impulse response of a 1 st order system is given below. • Find out – – – Time constant T=2 D. C Gain K=6 Transfer Function Step Response Also Draw the Step response on your notebook

Example#1 • For step response integrate impulse response • We can find out C if initial condition is known e. g. cs(0)=0

Example#1 • If initial Conditions are not known then partial fraction expansion is a better choice

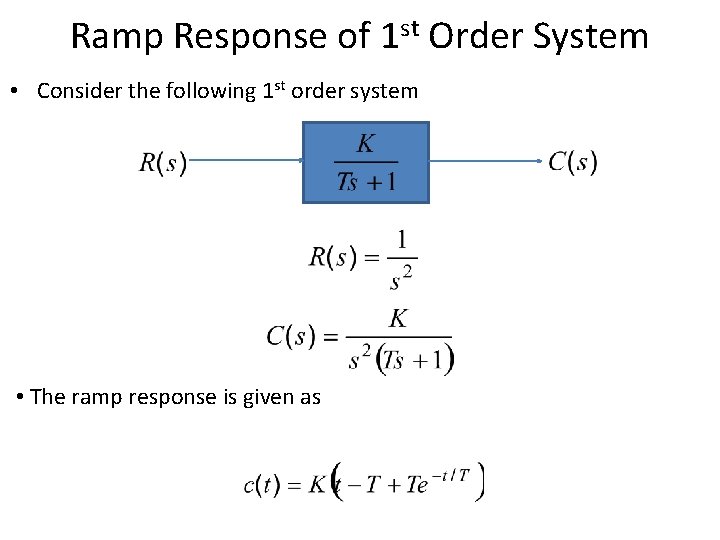
Ramp Response of 1 st Order System • Consider the following 1 st order system • The ramp response is given as

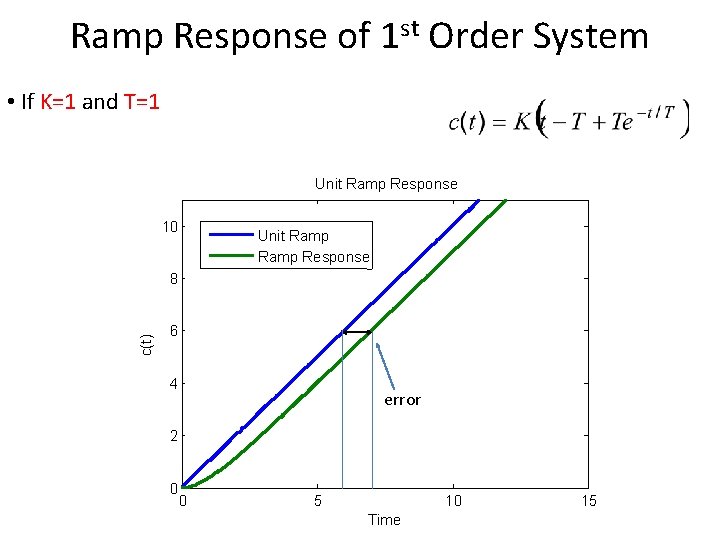
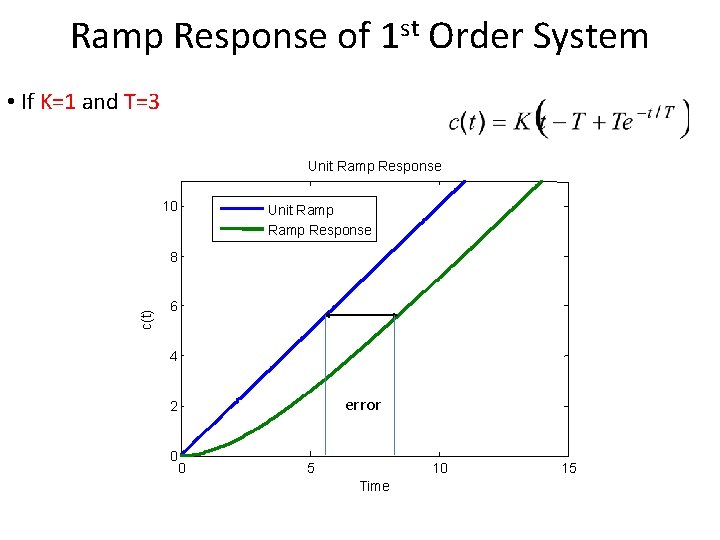
Ramp Response of 1 st Order System • If K=1 and T=1 Unit Ramp Response 10 Unit Ramp Response c(t) 8 6 4 error 2 0 0 5 10 Time 15

Ramp Response of 1 st Order System • If K=1 and T=3 Unit Ramp Response 10 Unit Ramp Response c(t) 8 6 4 error 2 0 0 5 10 Time 15

Parabolic Response of 1 st Order System • Consider the following 1 st order system Therefore, • Do it yourself

Practical Determination of Transfer Function of 1 st Order Systems • Often it is not possible or practical to obtain a system's transfer function analytically. • Perhaps the system is closed, and the component parts are not easily identifiable. • The system's step response can lead to a representation even though the inner construction is not known. • With a step input, we can measure the time constant and the steady-state value, from which the transfer function can be calculated.

Practical Determination of Transfer Function of 1 st Order Systems • If we can identify T and K from laboratory testing we can obtain the transfer function of the system.

Practical Determination of Transfer Function of 1 st Order Systems • For example, assume the unit step response given in figure. K=0. 72 • From the response, we can measure the time constant, that is, the time for the amplitude to reach 63% of its final value. • Since the final value is about 0. 72 the time constant is evaluated where the curve reaches 0. 63 x 0. 72 = 0. 45, or about 0. 13 second. • K is simply steady state value. T=0. 13 s • Thus transfer function is obtained as:

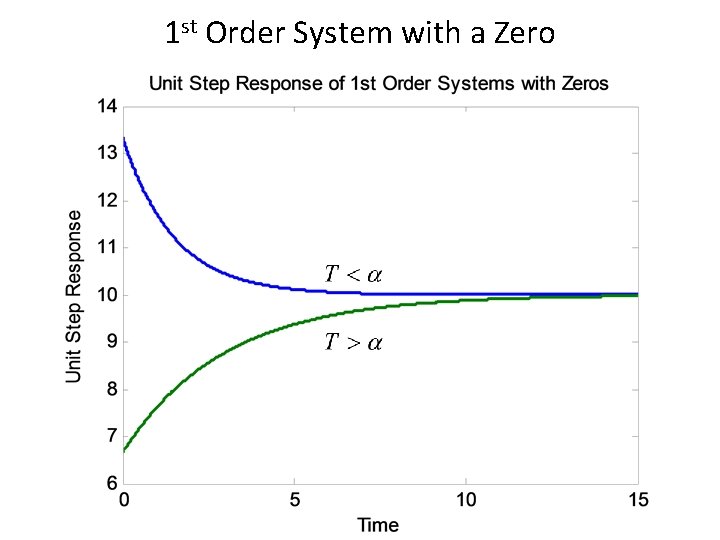
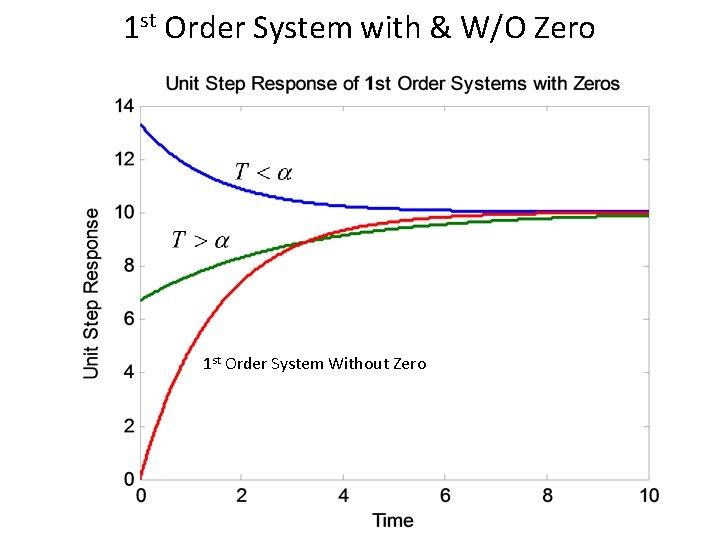
1 st Order System with a Zero • Zero of the system lie at -1/α and pole at -1/T. • Step response of the system would be:

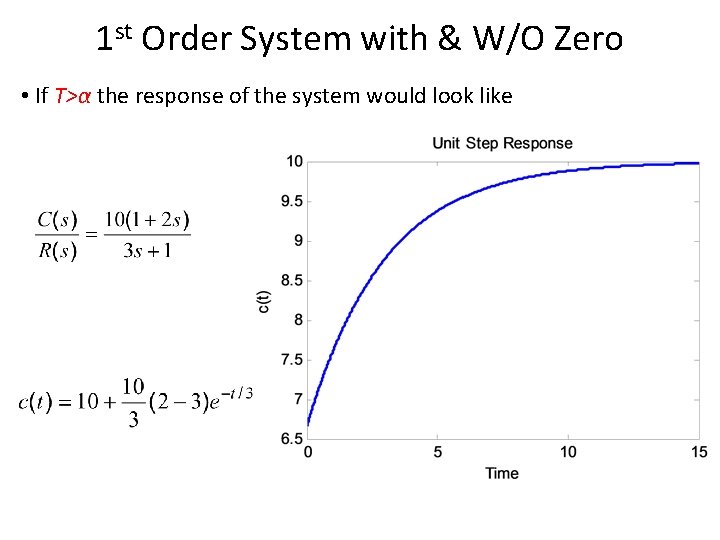
1 st Order System with & W/O Zero • If T>α the response will be same

1 st Order System with & W/O Zero • If T>α the response of the system would look like

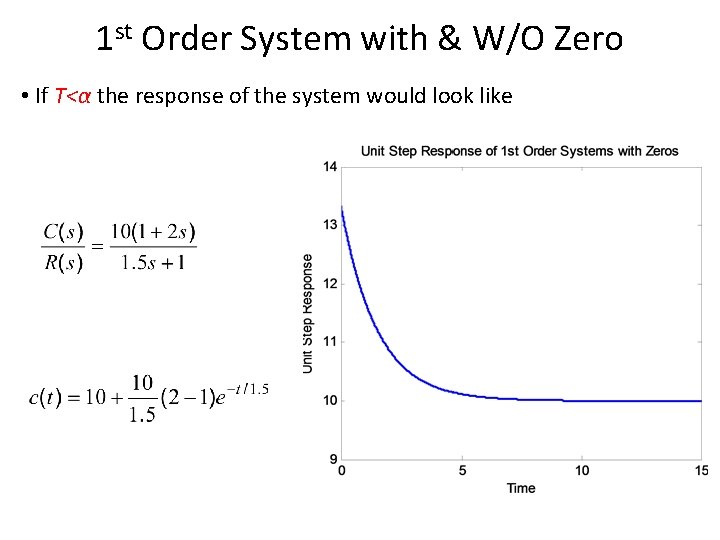
1 st Order System with & W/O Zero • If T<α the response of the system would look like

1 st Order System with a Zero

1 st Order System with & W/O Zero 1 st Order System Without Zero

Home Work • Find out the impulse, ramp and parabolic response of the system given below.

Example#2 • A thermometer requires 1 min to indicate 98% of the response to a step input. Assuming thermometer to be a first-order system, find the time constant. • If thermometer is placed in a bath, the temperature of which is changing linearly at a rate of 10°min, how much error does thermometer show?

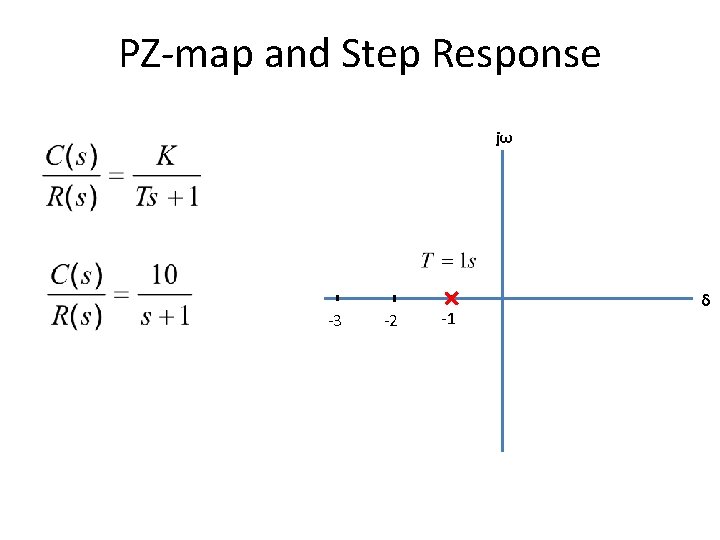
PZ-map and Step Response jω -3 -2 -1 δ

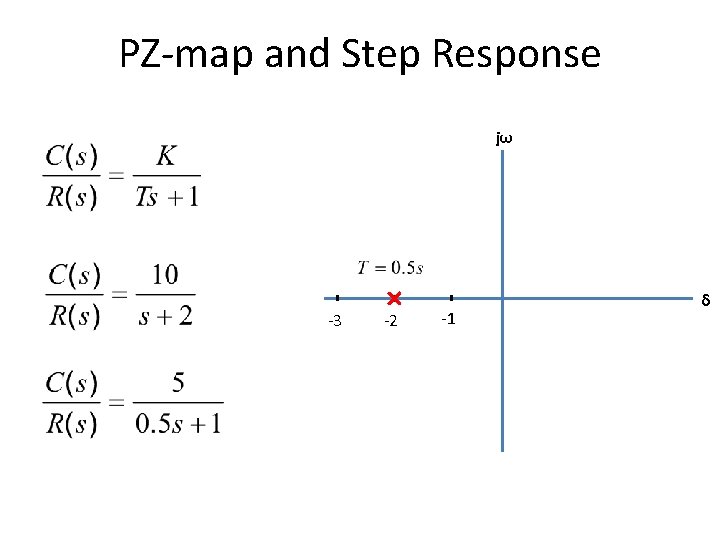
PZ-map and Step Response jω -3 -2 -1 δ

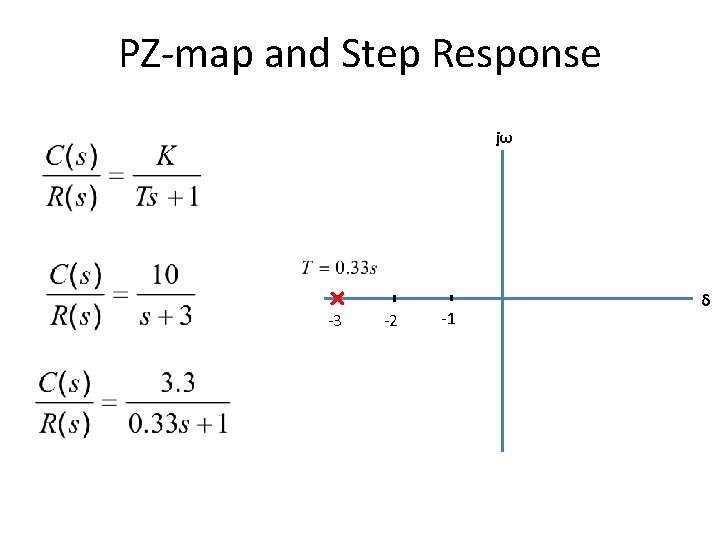
PZ-map and Step Response jω -3 -2 -1 δ

Comparison

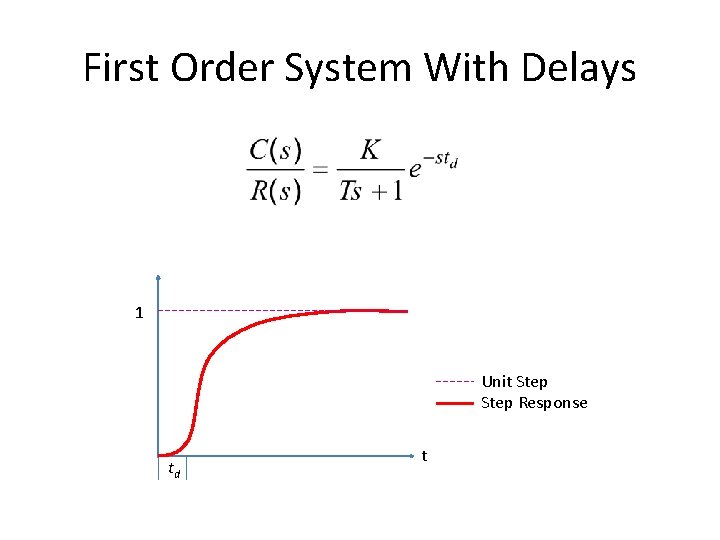
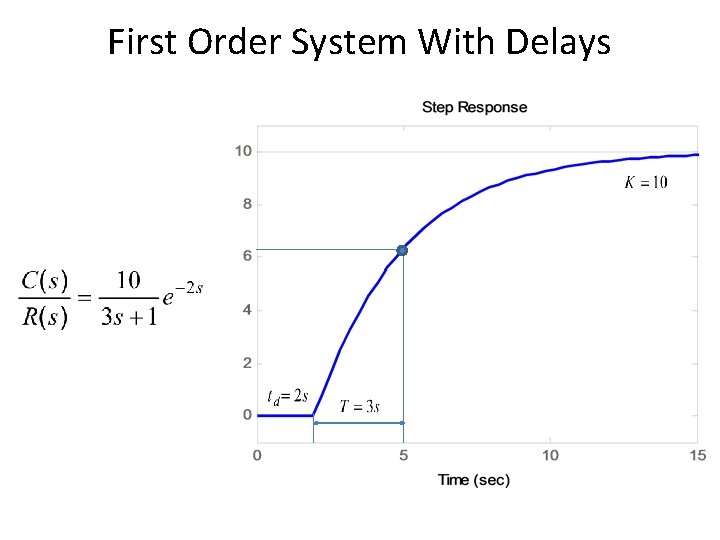
First Order System With Delays • Following transfer function is the generic representation of 1 st order system with time lag. • Where td is the delay time.

First Order System With Delays 1 Unit Step Response td t

First Order System With Delays

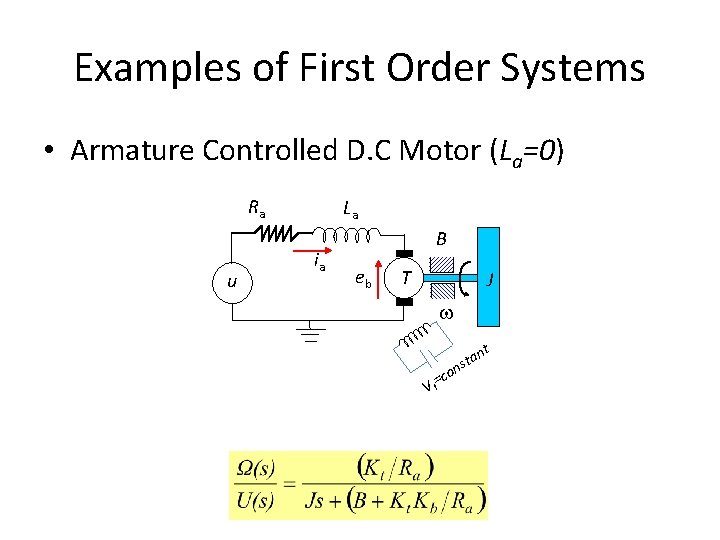
Examples of First Order Systems • Armature Controlled D. C Motor (La=0) Ra u La ia B eb T J t co an t s n V f=

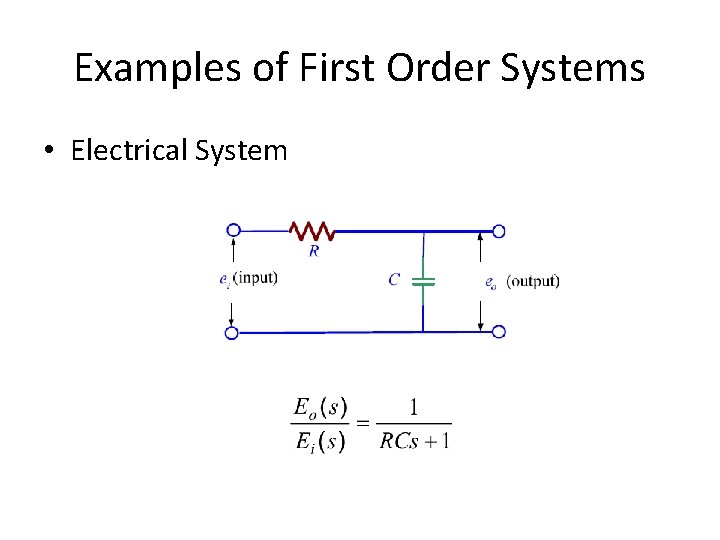
Examples of First Order Systems • Electrical System

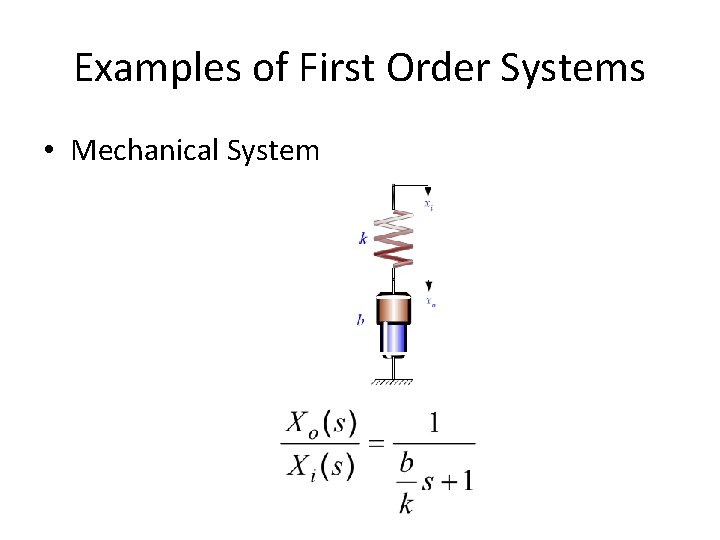
Examples of First Order Systems • Mechanical System

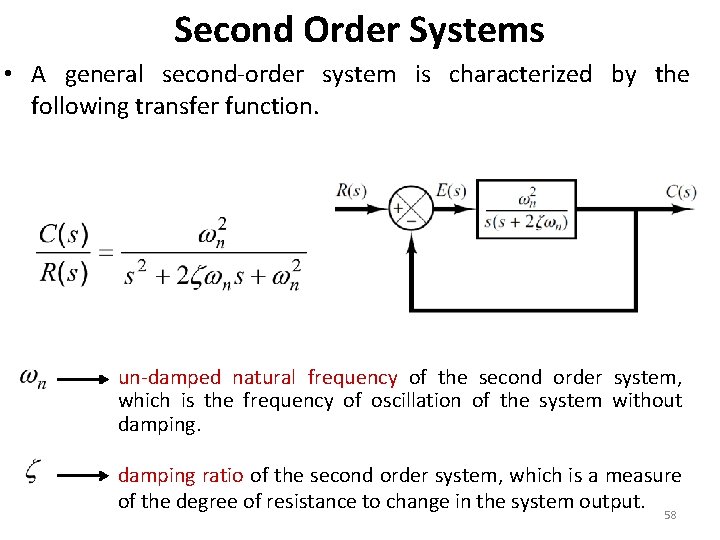
Second Order Systems • We have already discussed the affect of location of poles and zeros on the transient response of 1 st order systems. • Compared to the simplicity of a first-order system, a second-order system exhibits a wide range of responses that must be analyzed and described. • Varying a first-order system's parameter (T, K) simply changes the speed and offset of the response • Whereas, changes in the parameters of a second-order system can change the form of the response. • A second-order system can display characteristics much like a first-order 57 system or, depending on component values, display damped or pure

Second Order Systems • A general second-order system is characterized by the following transfer function. un-damped natural frequency of the second order system, which is the frequency of oscillation of the system without damping ratio of the second order system, which is a measure of the degree of resistance to change in the system output. 58

Example#3 • Determine the un-damped natural frequency and damping ratio of the following second order system. • Compare the numerator and denominator of the given transfer function with the general 2 nd order transfer function. 59

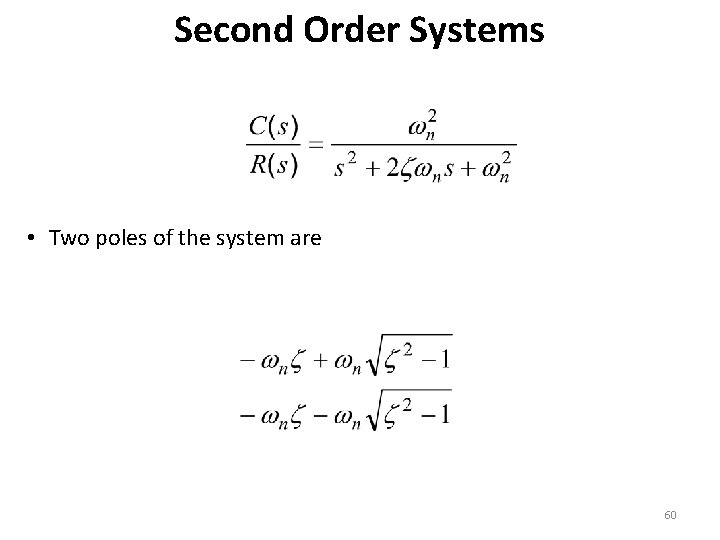
Second Order Systems • Two poles of the system are 60

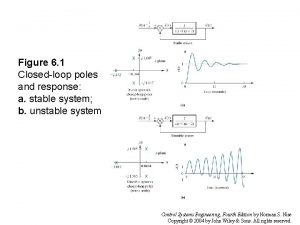
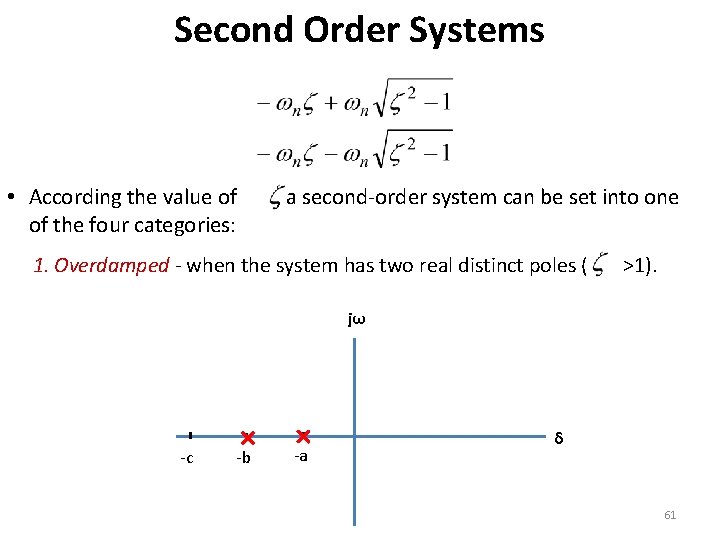
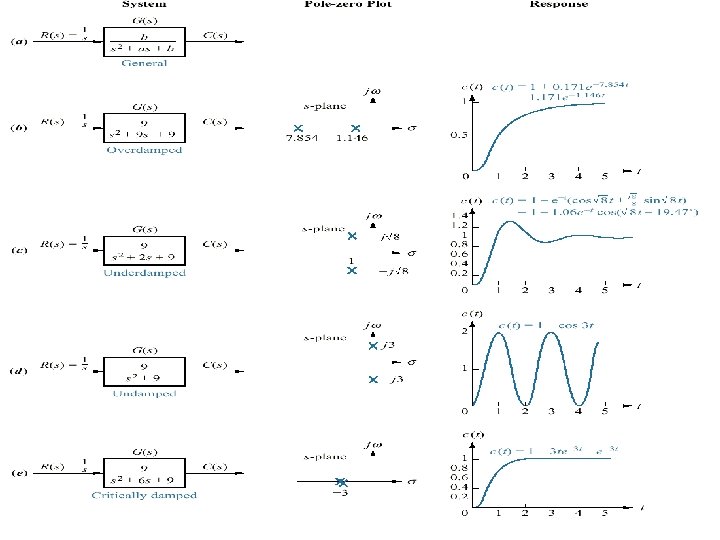
Second Order Systems • According the value of of the four categories: , a second-order system can be set into one 1. Overdamped - when the system has two real distinct poles ( >1). jω -c -b -a δ 61

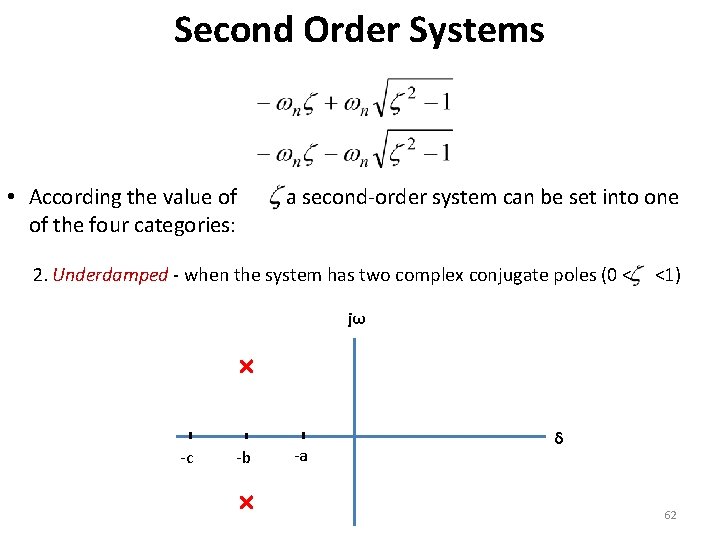
Second Order Systems • According the value of of the four categories: , a second-order system can be set into one 2. Underdamped - when the system has two complex conjugate poles (0 < <1) jω -c -b -a δ 62

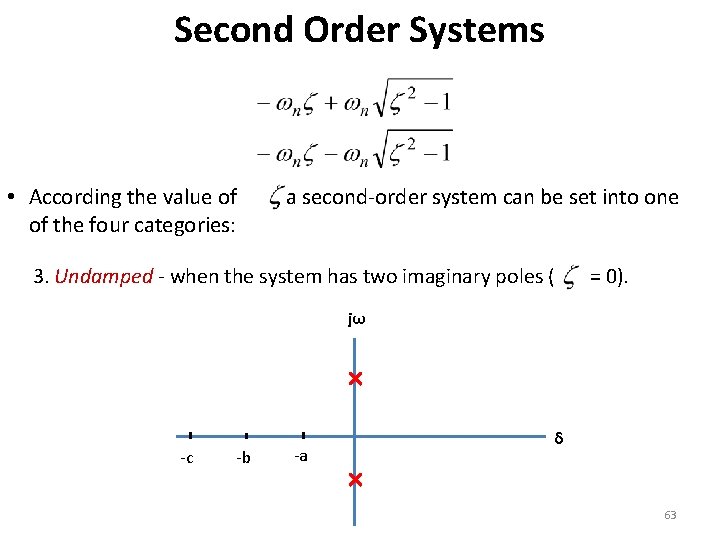
Second Order Systems • According the value of of the four categories: , a second-order system can be set into one 3. Undamped - when the system has two imaginary poles ( = 0). jω -c -b -a δ 63

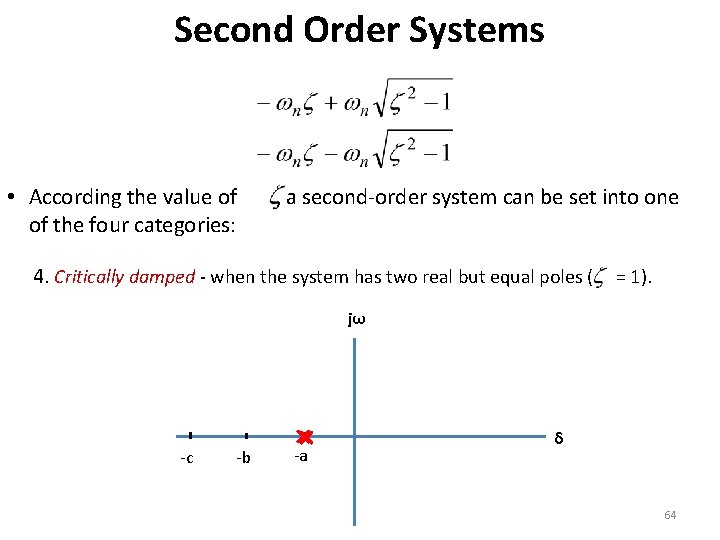
Second Order Systems • According the value of of the four categories: , a second-order system can be set into one 4. Critically damped - when the system has two real but equal poles ( = 1). jω -c -b -a δ 64

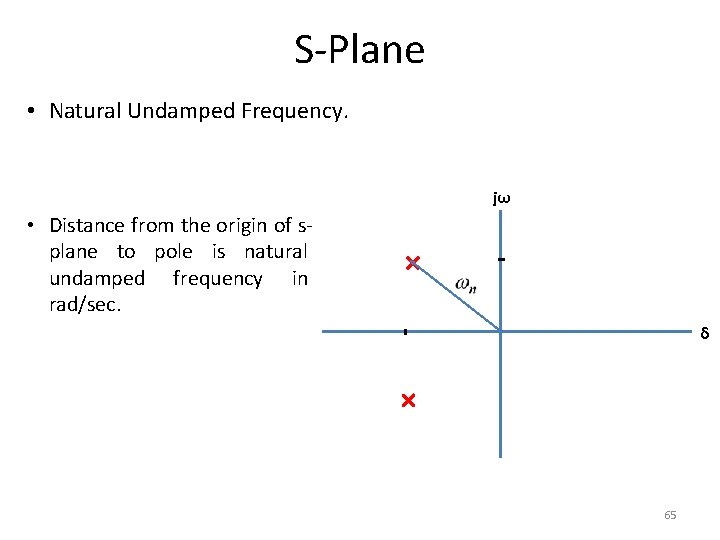
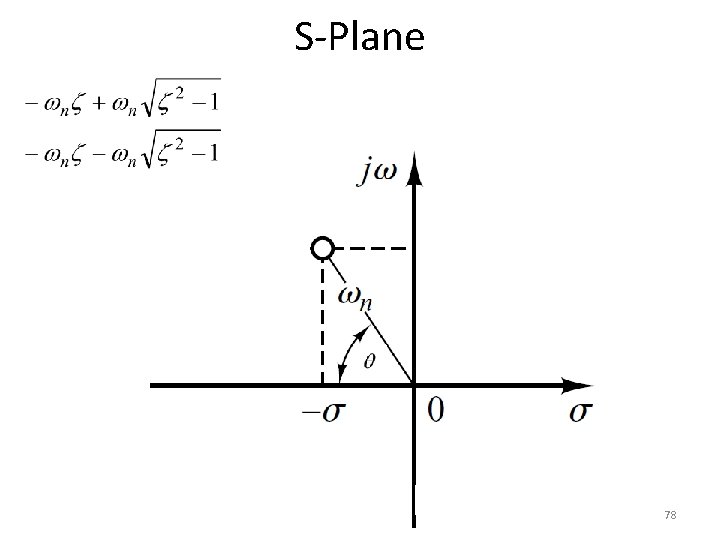
S-Plane • Natural Undamped Frequency. jω • Distance from the origin of splane to pole is natural undamped frequency in rad/sec. δ 65

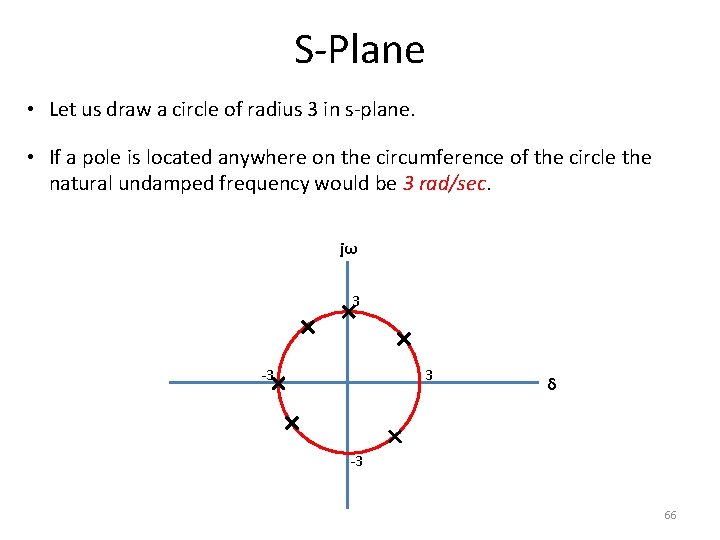
S-Plane • Let us draw a circle of radius 3 in s-plane. • If a pole is located anywhere on the circumference of the circle the natural undamped frequency would be 3 rad/sec. jω 3 -3 3 δ -3 66

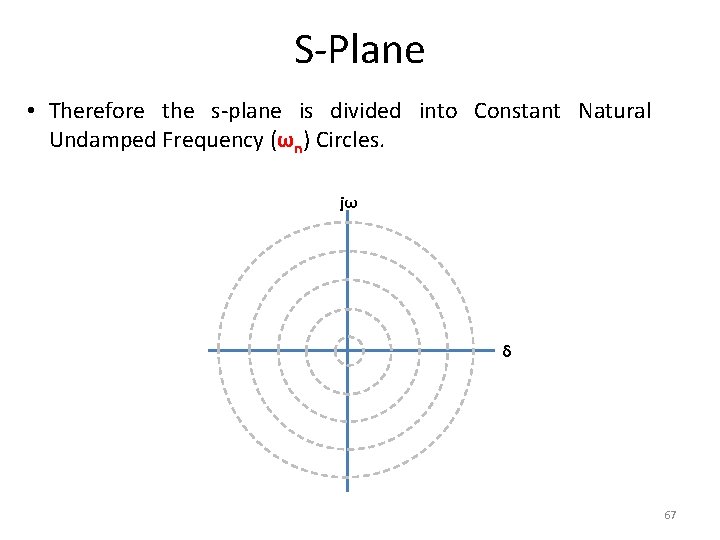
S-Plane • Therefore the s-plane is divided into Constant Natural Undamped Frequency (ωn) Circles. jω δ 67

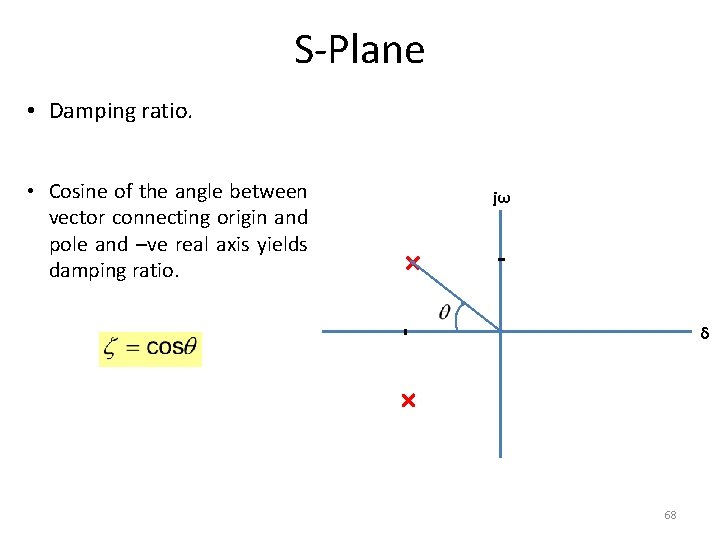
S-Plane • Damping ratio. • Cosine of the angle between vector connecting origin and pole and –ve real axis yields damping ratio. jω δ 68

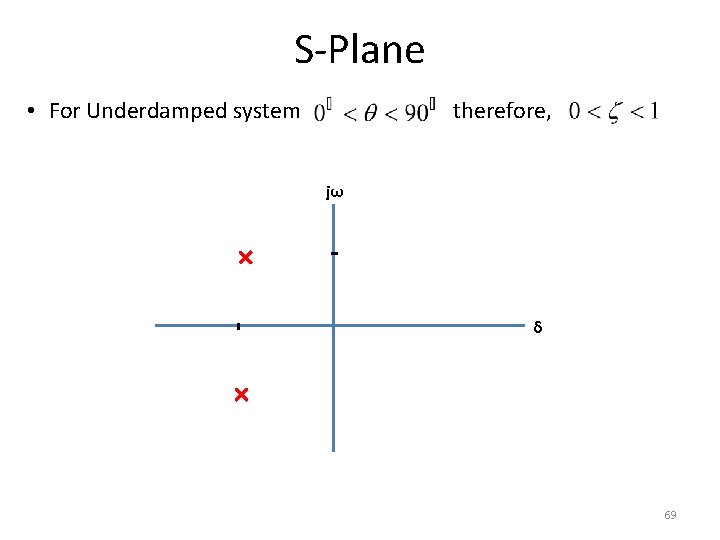
S-Plane • For Underdamped system therefore, jω δ 69

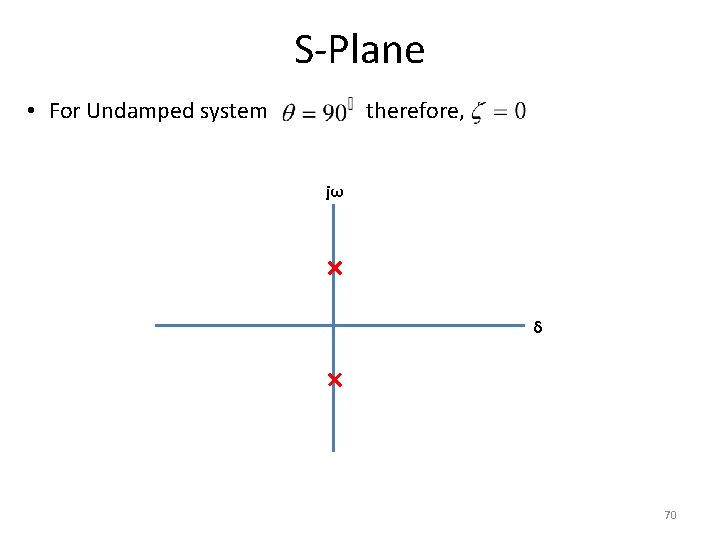
S-Plane • For Undamped system therefore, jω δ 70

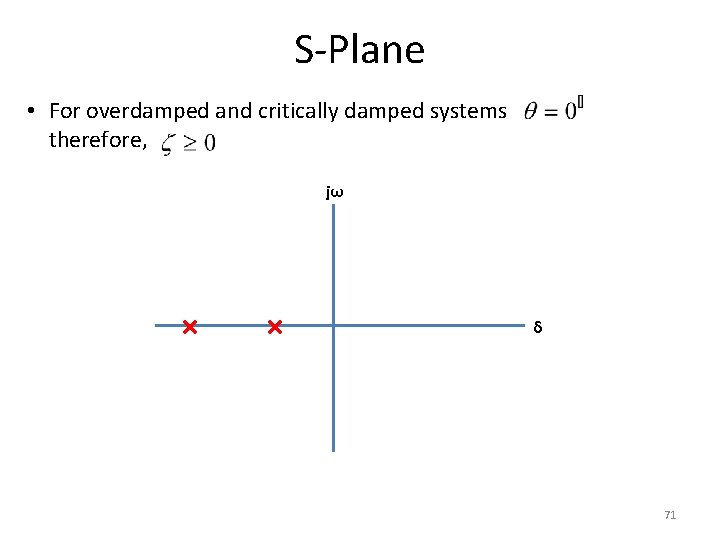
S-Plane • For overdamped and critically damped systems therefore, jω δ 71

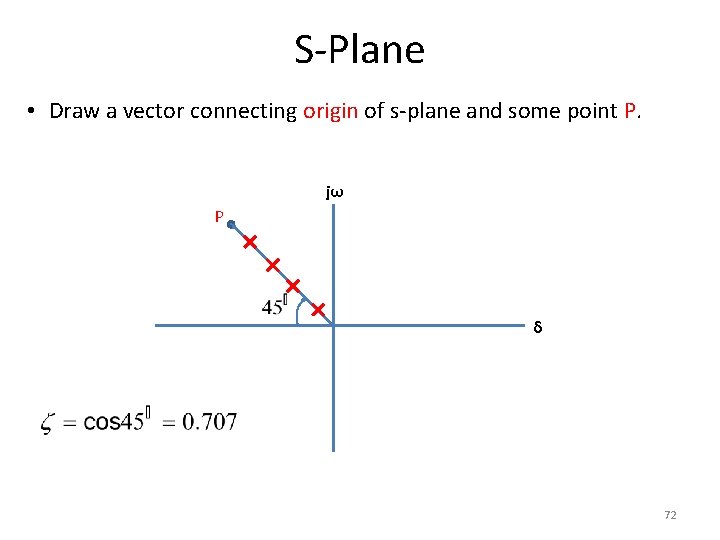
S-Plane • Draw a vector connecting origin of s-plane and some point P. jω P δ 72

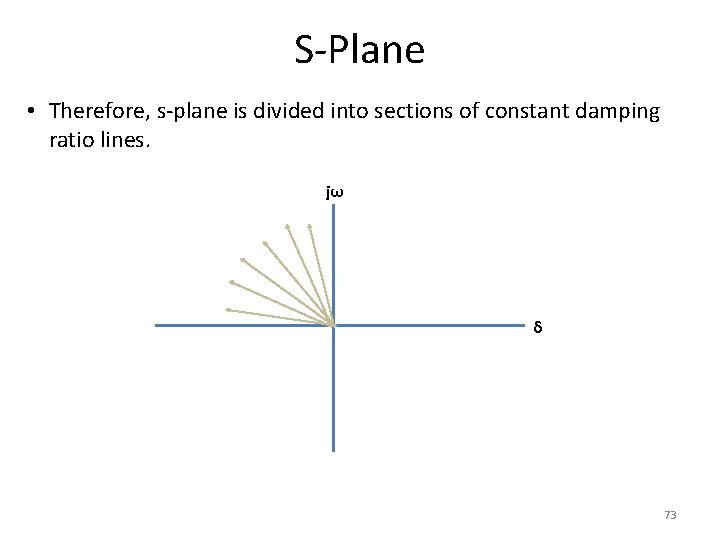
S-Plane • Therefore, s-plane is divided into sections of constant damping ratio lines. jω δ 73

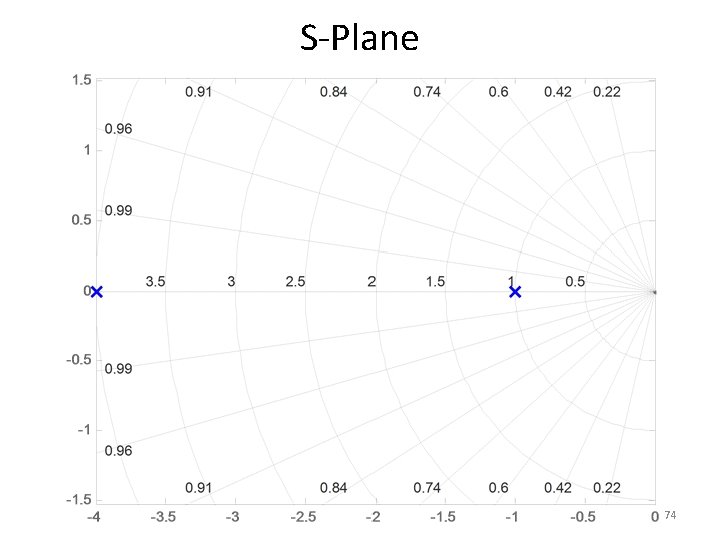
S-Plane 74

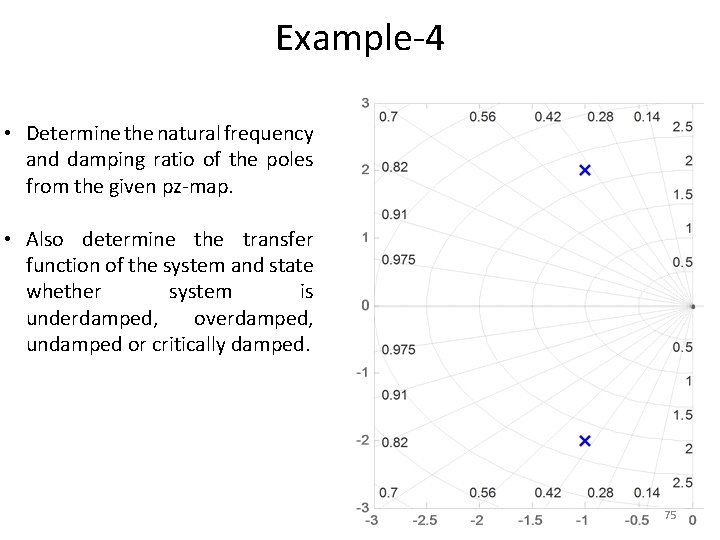
Example-4 • Determine the natural frequency and damping ratio of the poles from the given pz-map. • Also determine the transfer function of the system and state whether system is underdamped, overdamped, undamped or critically damped. 75

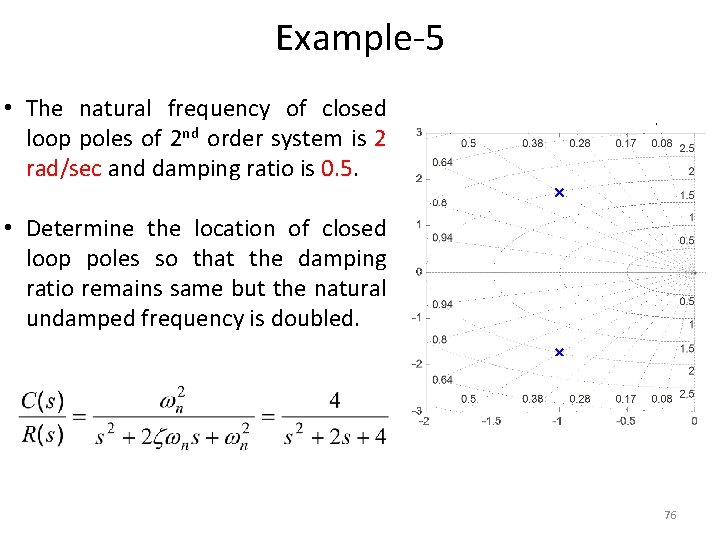
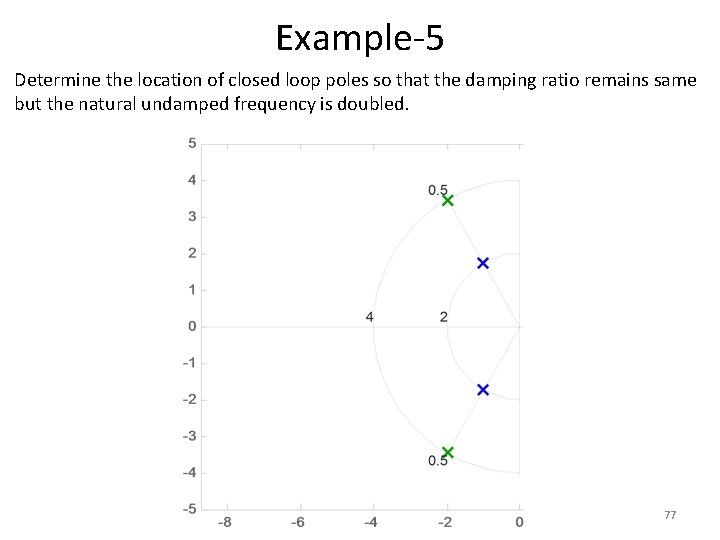
Example-5 • The natural frequency of closed loop poles of 2 nd order system is 2 rad/sec and damping ratio is 0. 5. • Determine the location of closed loop poles so that the damping ratio remains same but the natural undamped frequency is doubled. 76

Example-5 • Determine the location of closed loop poles so that the damping ratio remains same but the natural undamped frequency is doubled. 77

S-Plane 78

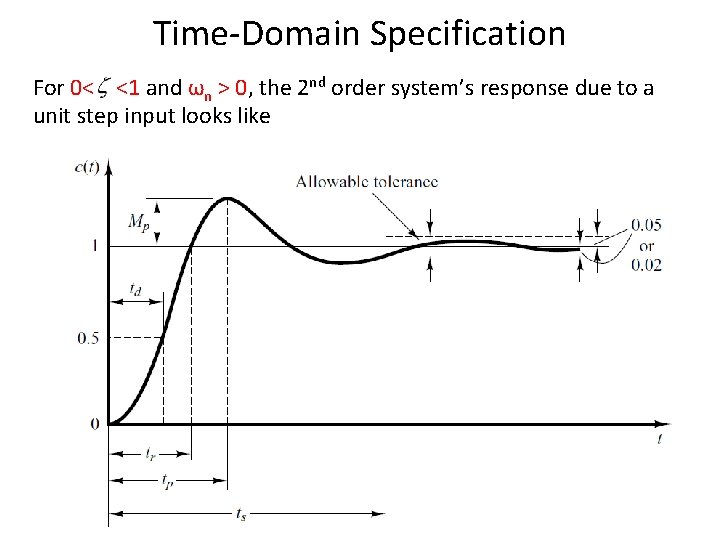
Time-Domain Specification For 0< <1 and ωn > 0, the 2 nd order system’s response due to a unit step input looks like 79

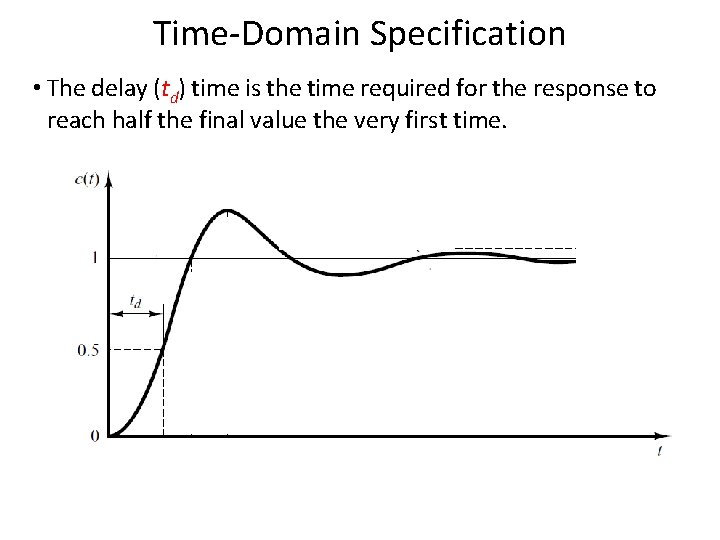
Time-Domain Specification • The delay (td) time is the time required for the response to reach half the final value the very first time. 80

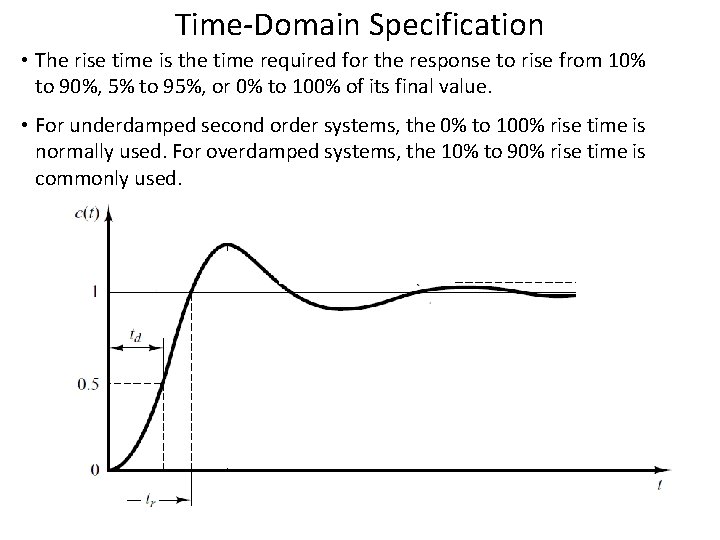
Time-Domain Specification • The rise time is the time required for the response to rise from 10% to 90%, 5% to 95%, or 0% to 100% of its final value. • For underdamped second order systems, the 0% to 100% rise time is normally used. For overdamped systems, the 10% to 90% rise time is commonly used.

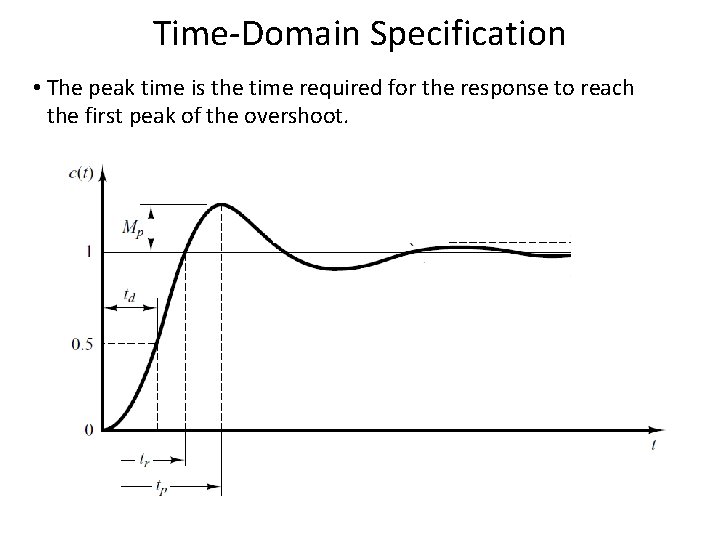
Time-Domain Specification • The peak time is the time required for the response to reach the first peak of the overshoot. 82 82

Time-Domain Specification The maximum overshoot is the maximum peak value of the response curve measured from unity. If the final steady-state value of the response differs from unity, then it is common to use the maximum percent overshoot. It is defined by The amount of the maximum (percent) overshoot directly indicates the relative stability of the system. 83

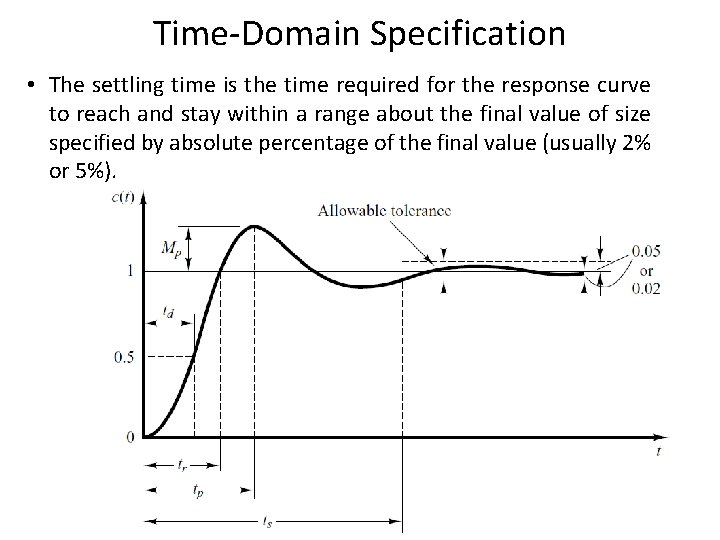
Time-Domain Specification • The settling time is the time required for the response curve to reach and stay within a range about the final value of size specified by absolute percentage of the final value (usually 2% or 5%). 84

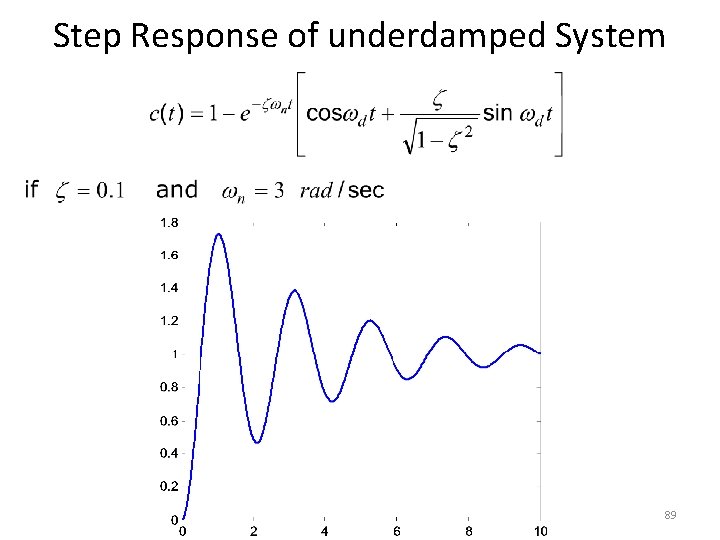
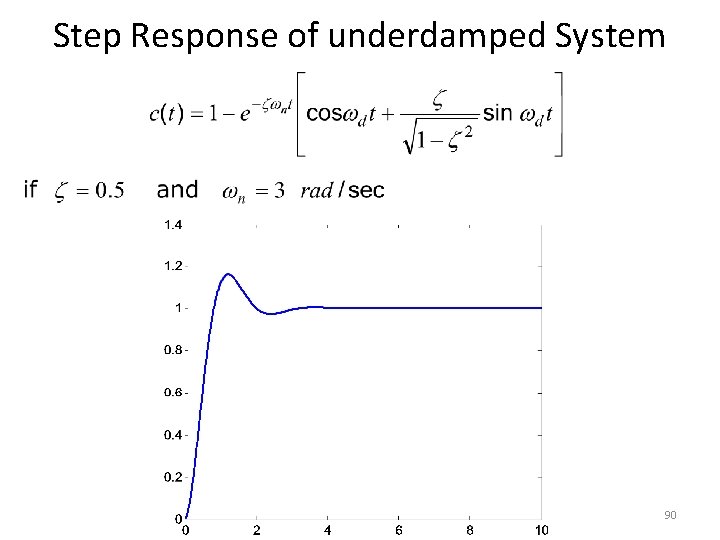
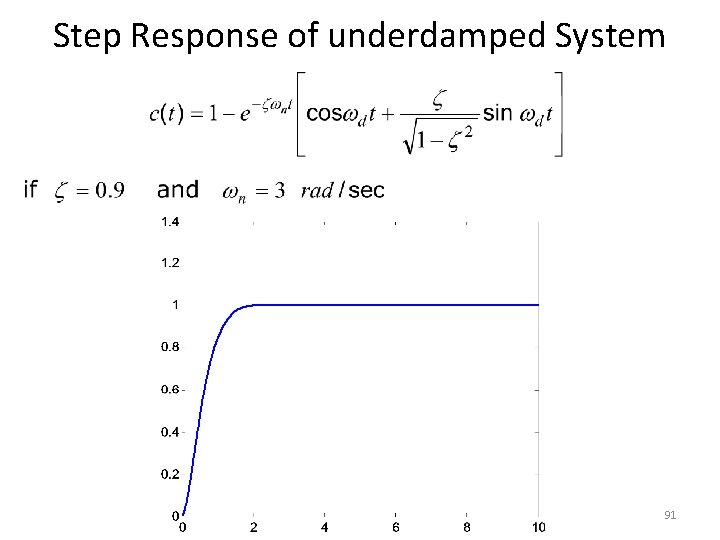
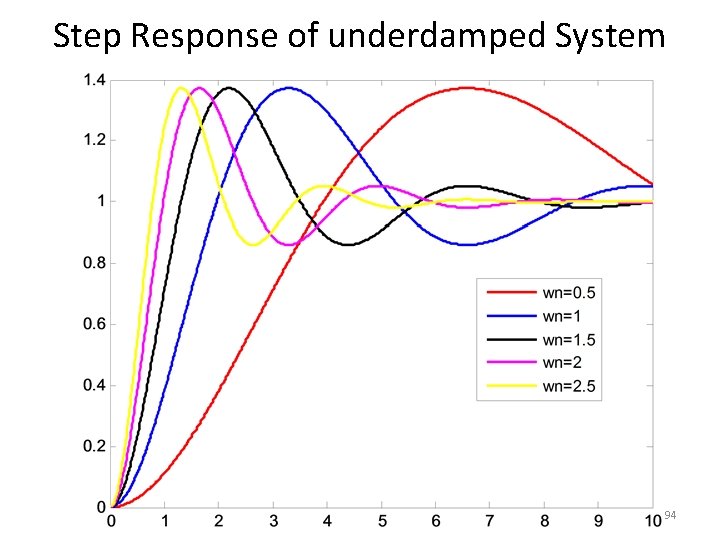
Step Response of underdamped System Step Response • The partial fraction expansion of above equation is given as 85

Step Response of underdamped System • Above equation can be written as • Where , is the frequency of transient oscillations and is called damped frequency. • The inverse Laplace transform of above equation can be obtained easily if C(s) is written in the following form: 86

Step Response of underdamped System 87

Step Response of underdamped System • When 88

Step Response of underdamped System 89

Step Response of underdamped System 90

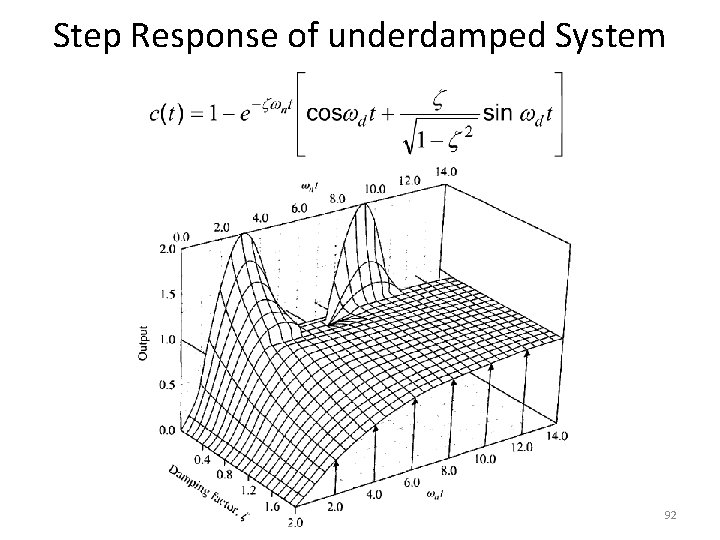
Step Response of underdamped System 91

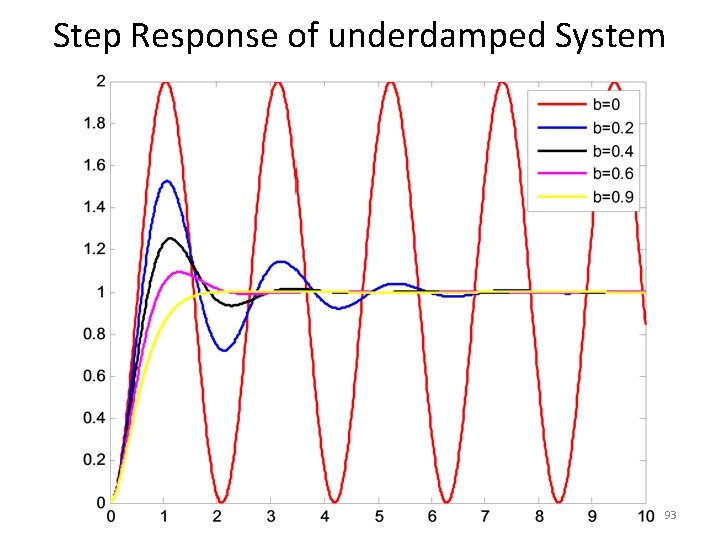
Step Response of underdamped System 92

Step Response of underdamped System 93

Step Response of underdamped System 94

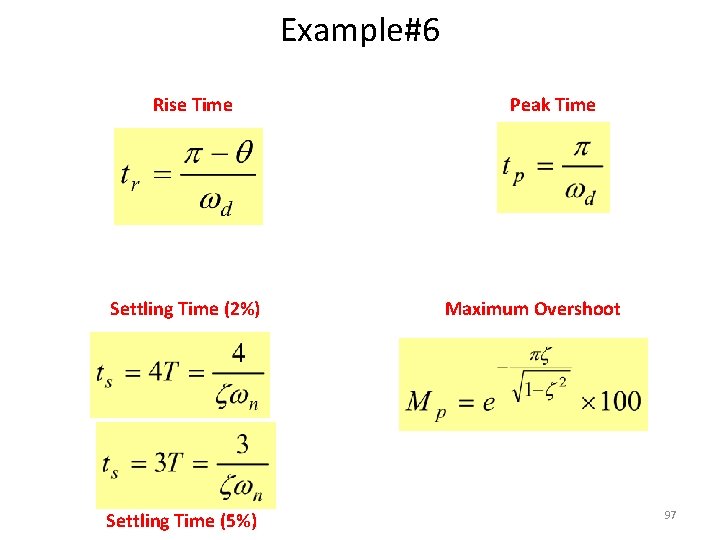
Time Domain Specifications Rise Time Peak Time Settling Time (2%) Maximum Overshoot Settling Time (5%) 95

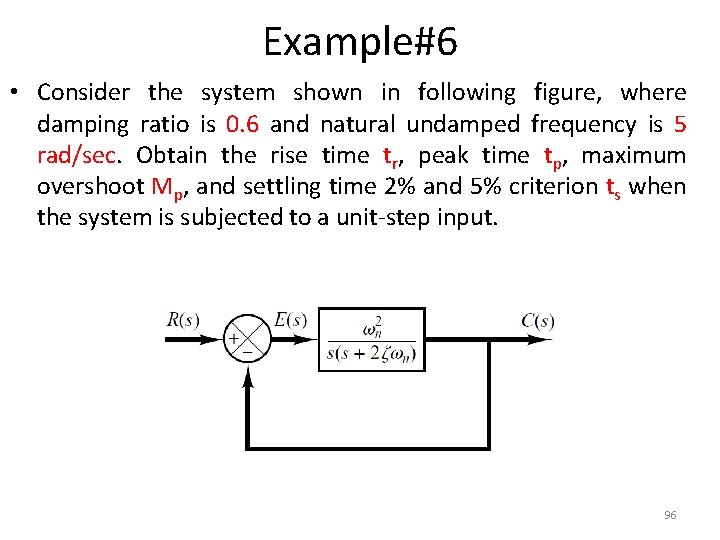
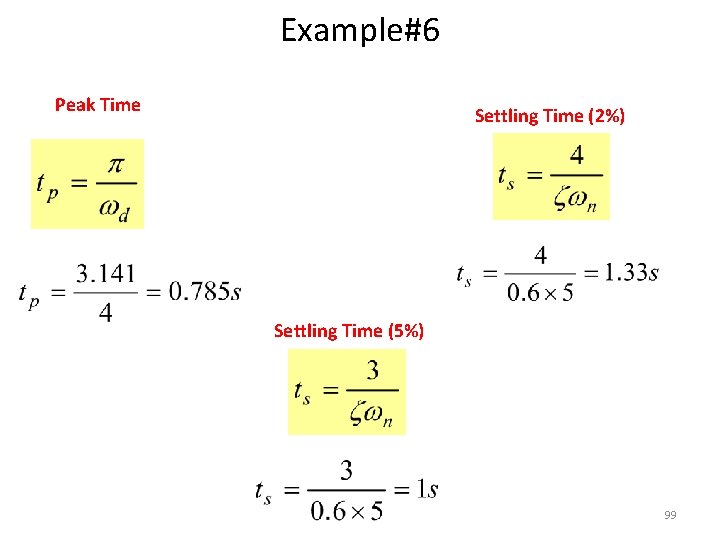
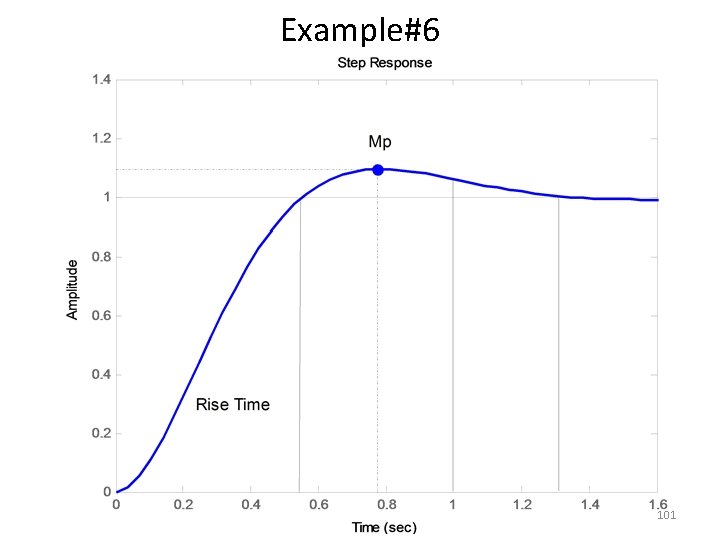
Example#6 • Consider the system shown in following figure, where damping ratio is 0. 6 and natural undamped frequency is 5 rad/sec. Obtain the rise time tr, peak time tp, maximum overshoot Mp, and settling time 2% and 5% criterion ts when the system is subjected to a unit-step input. 96

Example#6 Rise Time Settling Time (2%) Settling Time (5%) Peak Time Maximum Overshoot 97

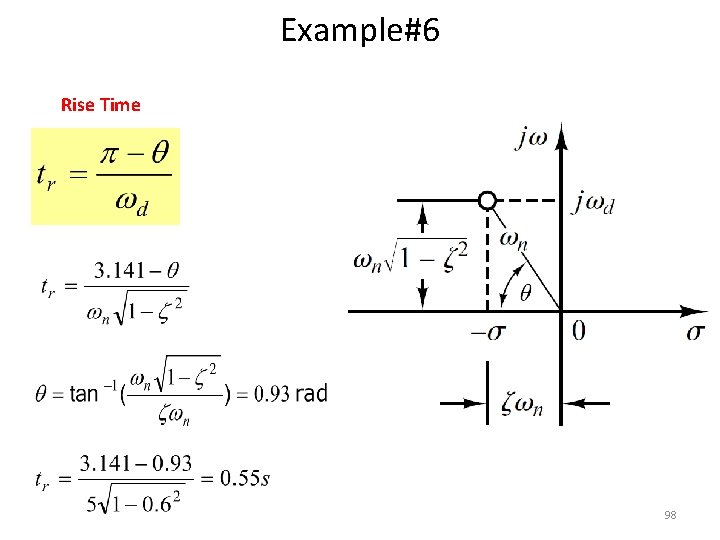
Example#6 Rise Time 98

Example#6 Peak Time Settling Time (2%) Settling Time (5%) 99

Example#6 Maximum Overshoot 100

Example#6 101

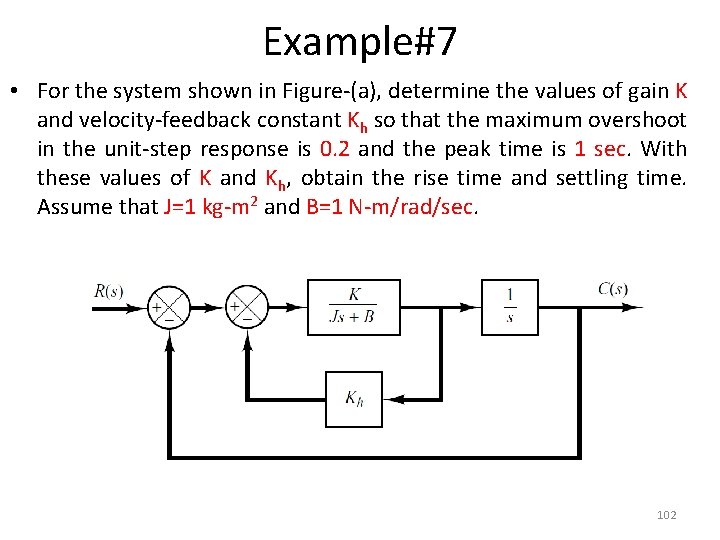
Example#7 • For the system shown in Figure-(a), determine the values of gain K and velocity-feedback constant Kh so that the maximum overshoot in the unit-step response is 0. 2 and the peak time is 1 sec. With these values of K and Kh, obtain the rise time and settling time. Assume that J=1 kg-m 2 and B=1 N-m/rad/sec. 102

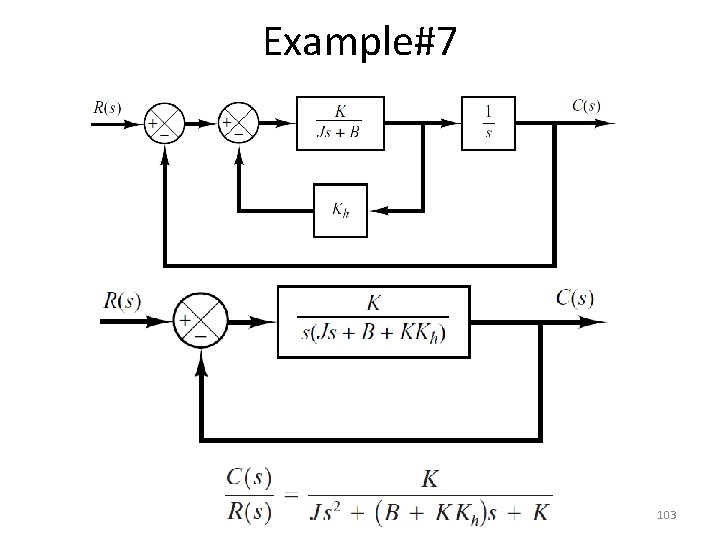
Example#7 103

Example#7 • Comparing above T. F with general 2 nd order T. F 104

Example#7 • Maximum overshoot is 0. 2. • The peak time is 1 sec 105

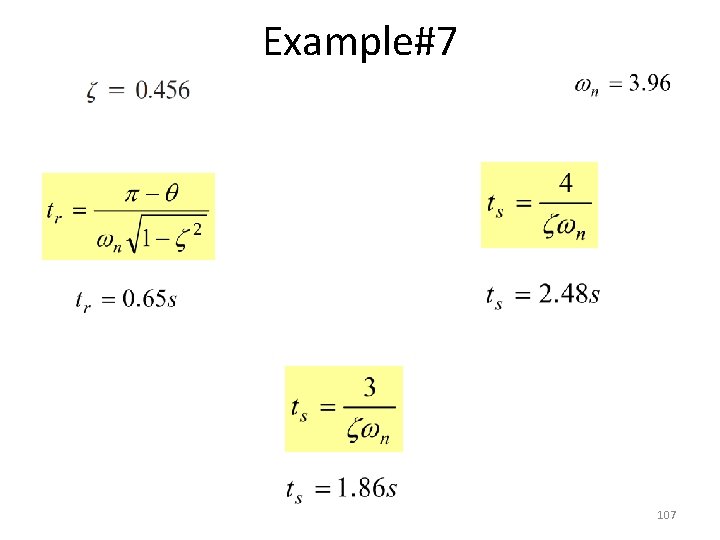
Example#7 106

Example#7 107

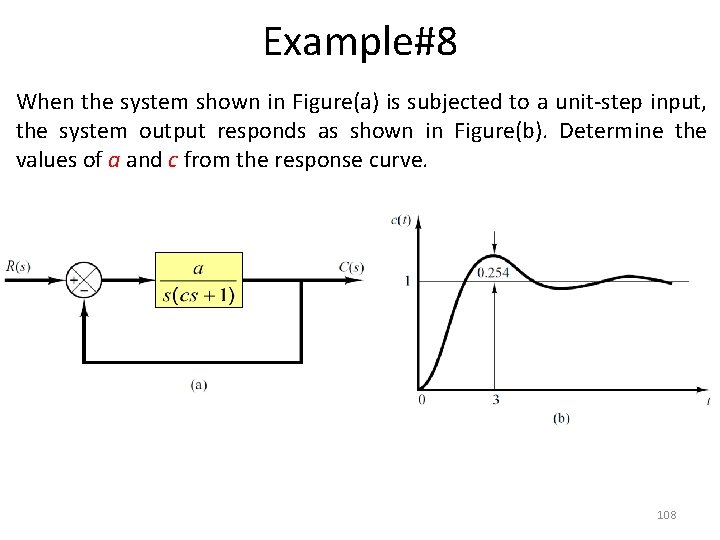
Example#8 When the system shown in Figure(a) is subjected to a unit-step input, the system output responds as shown in Figure(b). Determine the values of a and c from the response curve. 108

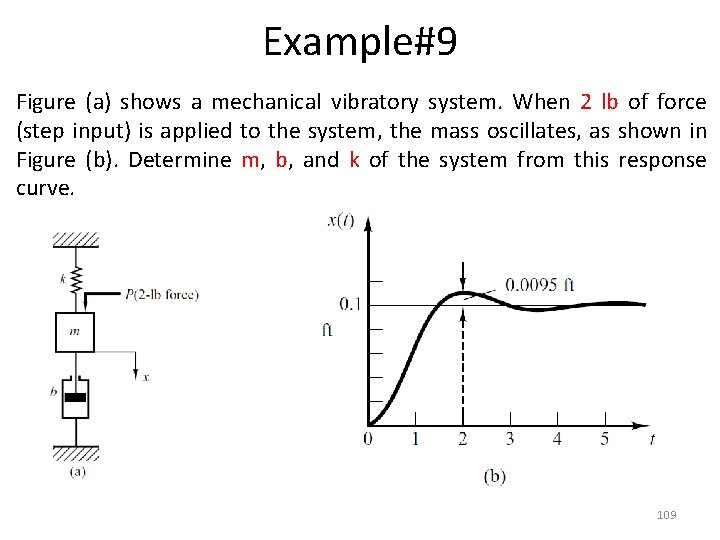
Example#9 Figure (a) shows a mechanical vibratory system. When 2 lb of force (step input) is applied to the system, the mass oscillates, as shown in Figure (b). Determine m, b, and k of the system from this response curve. 109

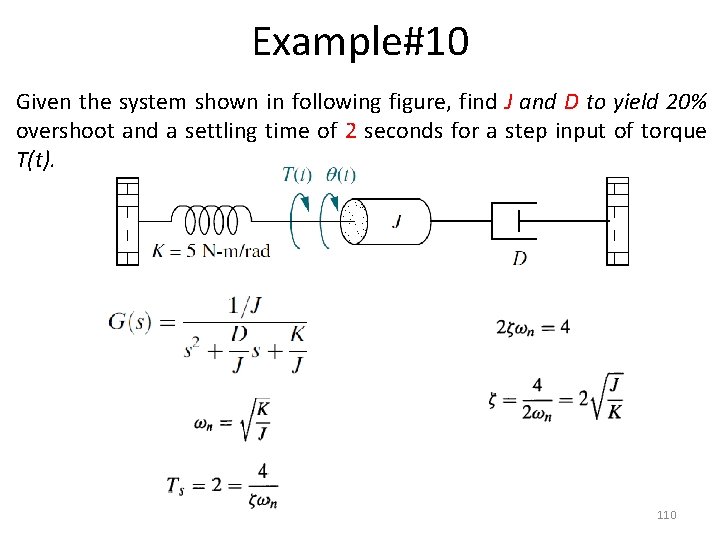
Example#10 Given the system shown in following figure, find J and D to yield 20% overshoot and a settling time of 2 seconds for a step input of torque T(t). 110

Example#10 111

Example#10 112

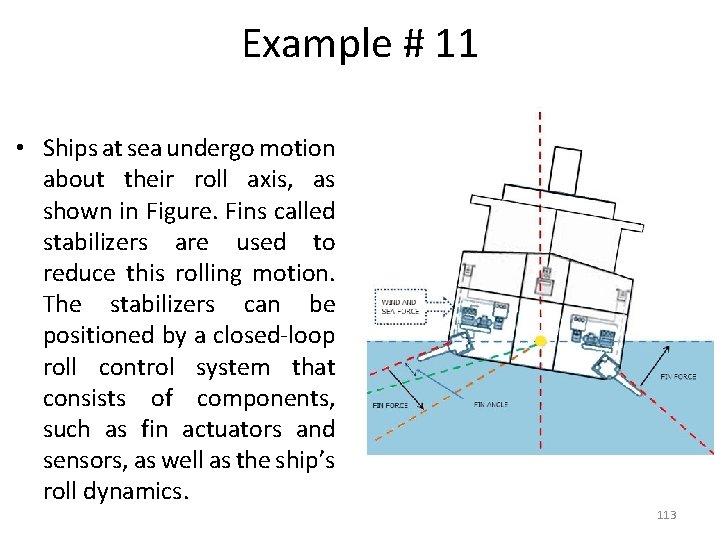
Example # 11 • Ships at sea undergo motion about their roll axis, as shown in Figure. Fins called stabilizers are used to reduce this rolling motion. The stabilizers can be positioned by a closed-loop roll control system that consists of components, such as fin actuators and sensors, as well as the ship’s roll dynamics. 113

Example # 11 • 114

Step Response of critically damped System ( ) Step Response • The partial fraction expansion of above equation is given as 115

116

Second – Order System Example 12: Describe the nature of the second-order system response via the value of the damping ratio for the systems with transfer function Do them as your own revision 117

Example-13 • For each of the transfer functions find the locations of the poles and zeros, plot them on the s-plane, and then write an expression for the general form of the step response without solving for the inverse Laplace transform. State the nature of each response (overdamped, underdamped, and so on). 118

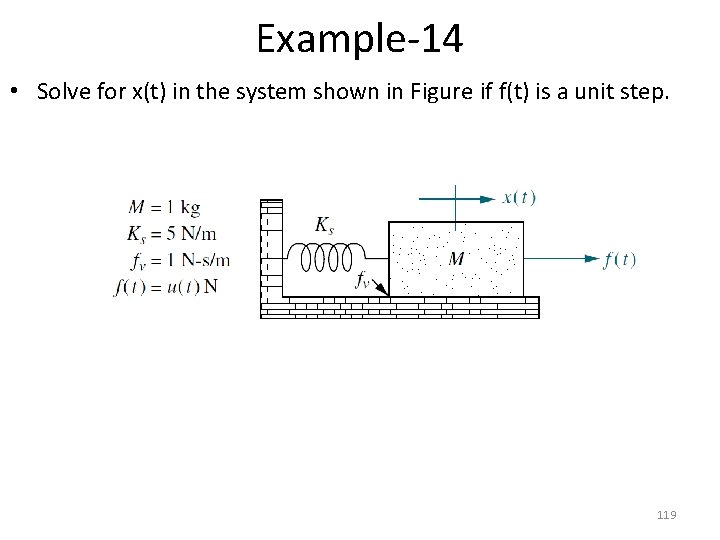
Example-14 • Solve for x(t) in the system shown in Figure if f(t) is a unit step. 119

To download this lecture visit http: //imtiazhussainkalwar. weebly. com/ END OF LECTURE-5