CIRCUNFERENCIA Y CIRCULO ngulos cuerdas y secantes en


















- Slides: 42

CIRCUNFERENCIA Y CIRCULO Ángulos, cuerdas y secantes en la circunferencia.

APRENDIZAJES ESPERADOS • Identificar los elementos primarios de Círculo y Circunferencia. • Calcular área y perímetro del sector circular. • Calcular ángulos en la circunferencia • Calcular medidas circunferencia de trazos en la

Contenidos 1. Definición 1. 1 Circunferencia 1. 2 Círculo 2. Elementos de la Circunferencia y del Círculo 2. 1 Radio 2. 2 Cuerda 2. 3 Diámetro 2. 4 Secante 2. 5 Tangente

2. 6 Sagita y Apotema 2. 7 Arco de circunferencia 2. 8 Sector Circular 2. 9 Segmento Circular 3. Áreas y Perímetros 3. 1 Área del Círculo 3. 2 Perímetro de la Circunferencia 3. 3 Medida de un arco de circunferencia 3. 4 Área y Perímetro de un sector circular 3. 5 Perímetro de un segmento circular

PARA RECORDAR…

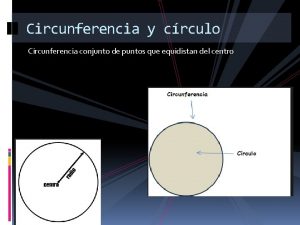
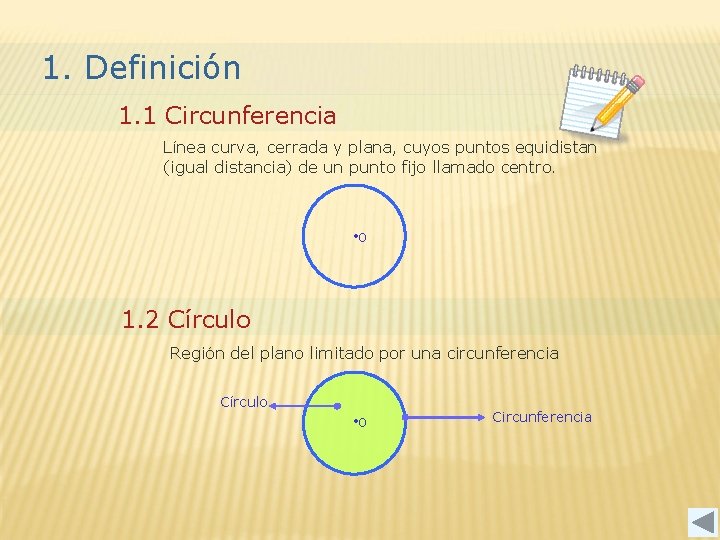
1. Definición 1. 1 Circunferencia Línea curva, cerrada y plana, cuyos puntos equidistan (igual distancia) de un punto fijo llamado centro. • o 1. 2 Círculo Región del plano limitado por una circunferencia Círculo • o Circunferencia

2. Elementos de la Circunferencia y del Círculo 2. 1 Radio (r) Segmento que une el centro de la circunferencia con cualquier punto de la circunferencia. o r A O: centro de la circunferencia OA: radio = r

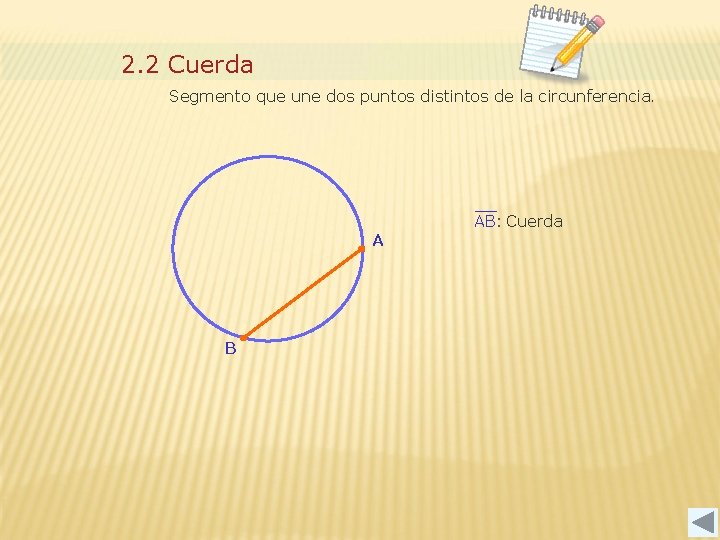
2. 2 Cuerda Segmento que une dos puntos distintos de la circunferencia. A B AB: Cuerda

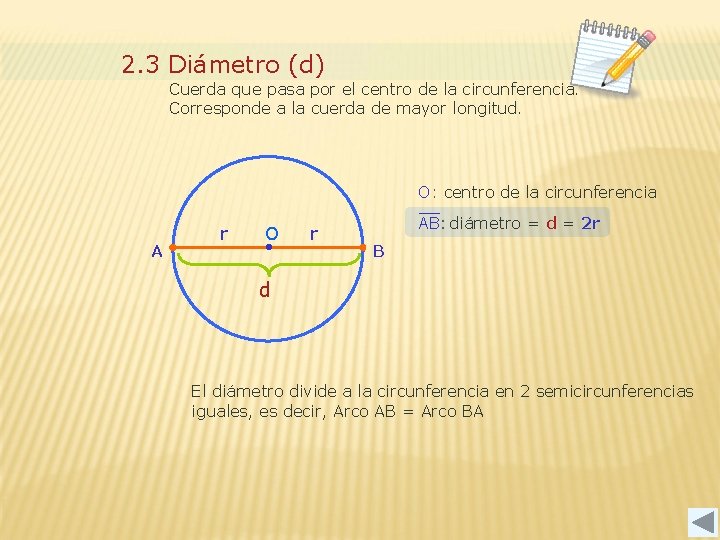
2. 3 Diámetro (d) Cuerda que pasa por el centro de la circunferencia. Corresponde a la cuerda de mayor longitud. O: centro de la circunferencia A r O • r AB: diámetro = d = 2 r B d El diámetro divide a la circunferencia en 2 semicircunferencias iguales, es decir, Arco AB = Arco BA

2. 4 Secante Recta que intersecta a la circunferencia en 2 puntos, formando una cuerda. A • AB: Cuerda • B AB: Secante

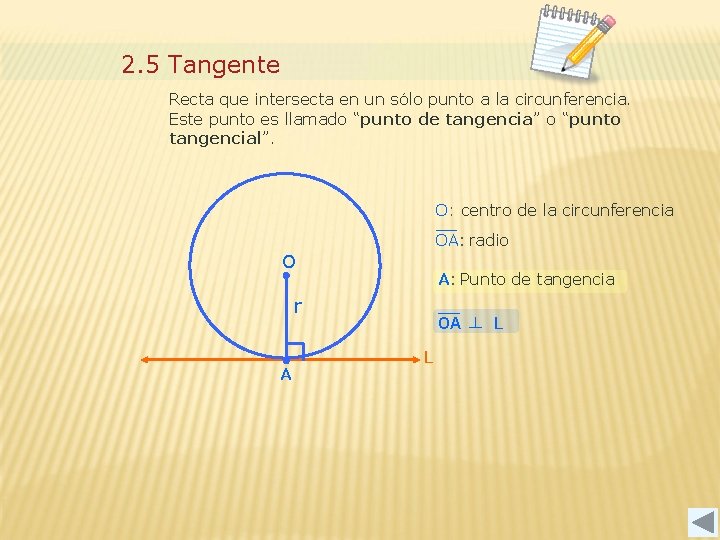
2. 5 Tangente Recta que intersecta en un sólo punto a la circunferencia. Este punto es llamado “punto de tangencia” o “punto tangencial”. O: centro de la circunferencia OA: radio O A: Punto de tangencia r A OA ┴ L L

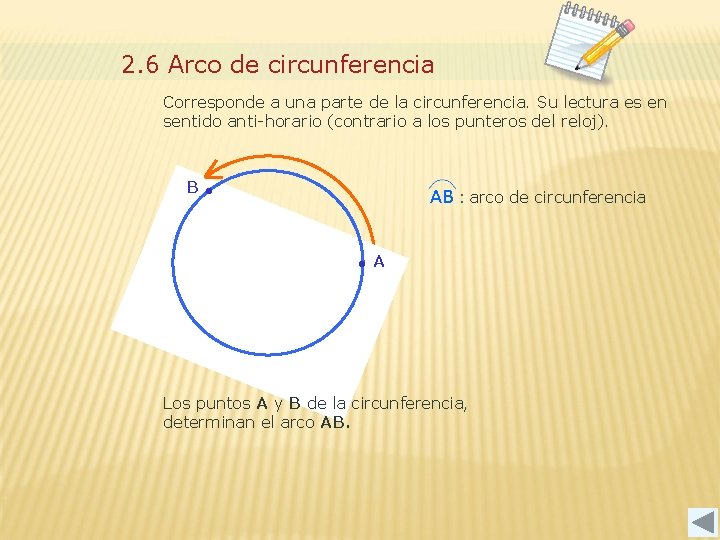
2. 6 Arco de circunferencia Corresponde a una parte de la circunferencia. Su lectura es en sentido anti-horario (contrario a los punteros del reloj). B • AB : arco de circunferencia • A Los puntos A y B de la circunferencia, determinan el arco AB.

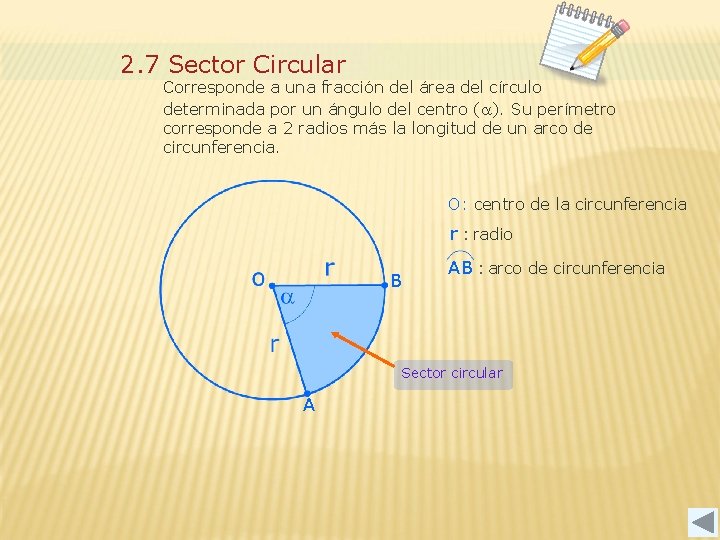
2. 7 Sector Circular Corresponde a una fracción del área del círculo determinada por un ángulo del centro ( ). Su perímetro corresponde a 2 radios más la longitud de un arco de circunferencia. O: centro de la circunferencia r : radio B AB : arco de circunferencia Sector circular A

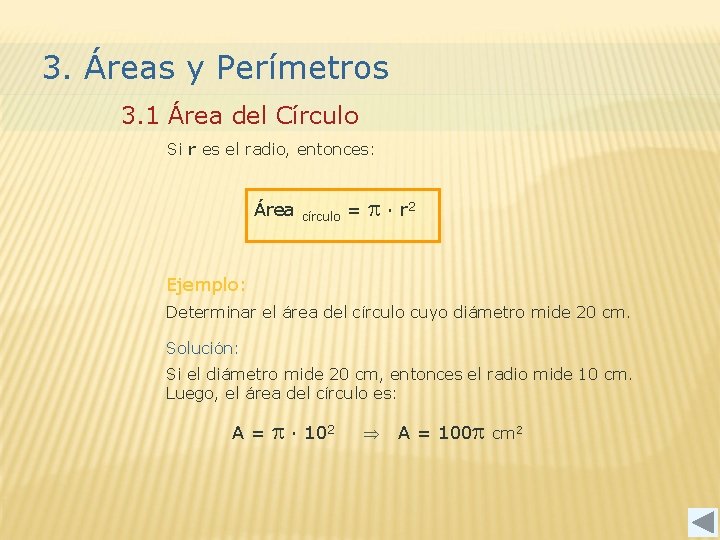
3. Áreas y Perímetros 3. 1 Área del Círculo Si r es el radio, entonces: Área círculo = p ∙ r 2 Ejemplo: Determinar el área del círculo cuyo diámetro mide 20 cm. Solución: Si el diámetro mide 20 cm, entonces el radio mide 10 cm. Luego, el área del círculo es: A= p ∙ 102 A = 100 p cm 2

3. 2 Perímetro de la circunferencia Si r es el radio y d el diámetro, entonces: Perímetro = 2 p∙r ó Perímetro = p∙d Ejemplo: Determinar el perímetro de una circunferencia cuyo radio mide 15 cm. Solución: P = 2 p∙ 15 P = 30 p cm.

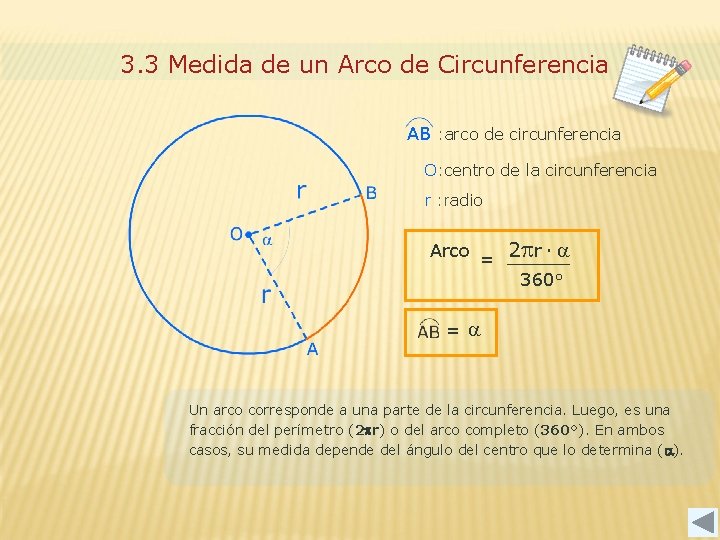
3. 3 Medida de un Arco de Circunferencia AB : arco de circunferencia O: centro de la circunferencia r : radio Arco = 2 pr ∙ 360° = Un arco corresponde a una parte de la circunferencia. Luego, es una fracción del perímetro (2 pr) o del arco completo (360°). En ambos casos, su medida depende del ángulo del centro que lo determina (a).

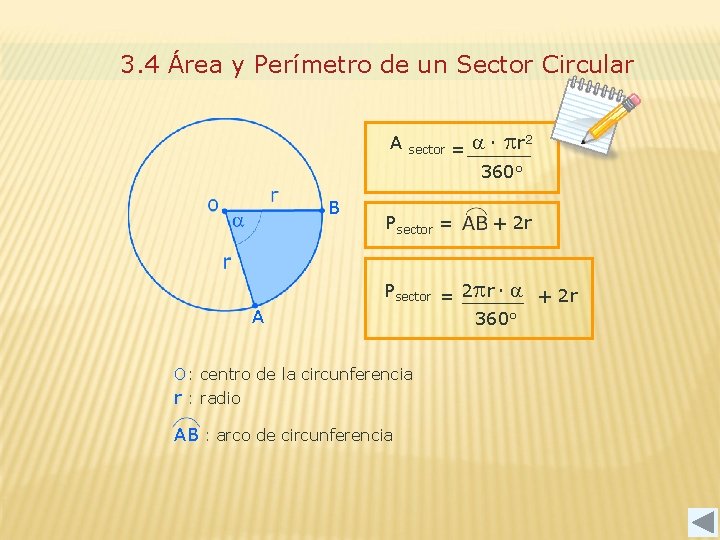
3. 4 Área y Perímetro de un Sector Circular A B A sector 2 = ∙ pr 360° Psector = + 2 r Psector = 2 pr ∙ + 2 r 360° O: centro de la circunferencia r : radio AB : arco de circunferencia

Ejemplo de aplicación: Determinar el área y perímetro de la zona achurada de la figura. O: centro de la circunferencia. Solución: A Sector 2 = 80∙p∙ 4 360° A Sector = 2∙p∙ 16 9 A Sector = 32 p 9 Psector = 2 p 4 ∙ 80+ 2∙ 4 360° Psector = 16 p + 8 9

Ángulos en la Circunferencia 1. Teoremas fundamentales - Ángulos 1. 1 Ángulo del centro y ángulo inscrito 1. 2 Igualdad de ángulos inscritos 1. 3 Triángulo inscrito en una semicircunferencia 1. 4 Cuadrilátero inscrito en una circunferencia 1. 5 Teorema del ángulo exterior 1. 6 Teorema del ángulo interior

2. Teoremas fundamentales - Trazos 2. 1 Teorema de las secantes 2. 2 Teorema de la tangente y la secante 2. 3 Teorema de las tangentes 2. 4 Teorema de las cuerdas 2. 5 Cuadrilátero circunscrito a una circunferencia

1. Teoremas fundamentales (ángulos) 1. 1 Ángulo del centro y ángulo inscrito Ángulo del centro: Tiene el vértice en el centro de la circunferencia, y mide lo mismo que el arco que subtiende. Ejemplo: Si el arco AB = 40º, entonces = 40º 40° O: centro de la circunferencia

Ángulo inscrito: Tiene el vértice en la circunferencia, y mide la mitad del arco que subtiende. Ejemplo: Si el arco AB = 50º, entonces = 25º 50°

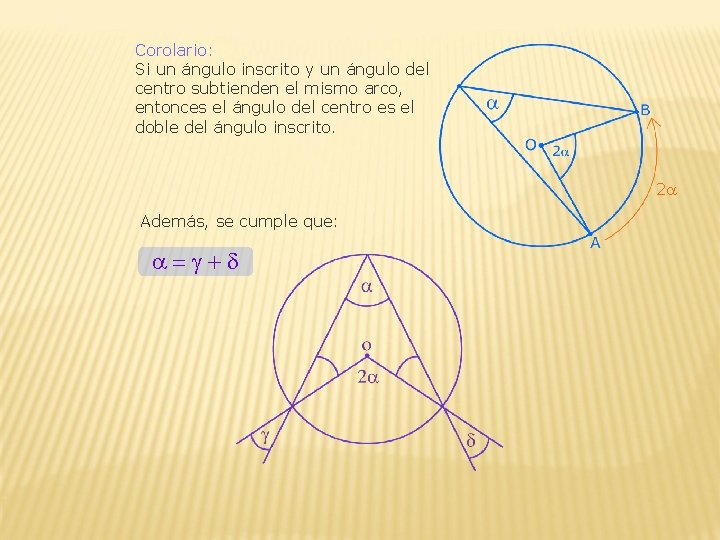
Corolario: Si un ángulo inscrito y un ángulo del centro subtienden el mismo arco, entonces el ángulo del centro es el doble del ángulo inscrito. 2 Además, se cumple que: =g+d

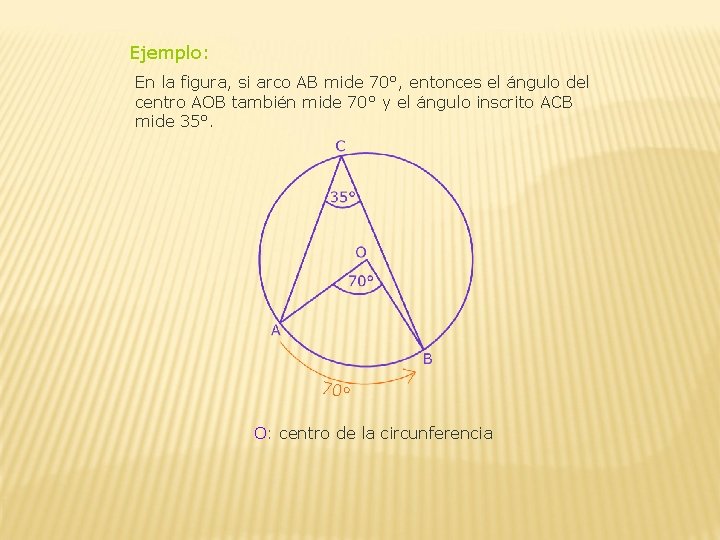
Ejemplo: En la figura, si arco AB mide 70°, entonces el ángulo del centro AOB también mide 70° y el ángulo inscrito ACB mide 35°. 70° O: centro de la circunferencia

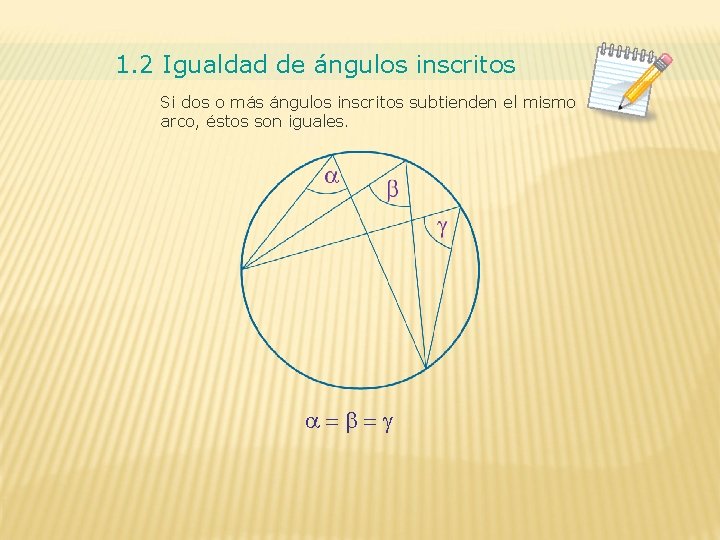
1. 2 Igualdad de ángulos inscritos Si dos o más ángulos inscritos subtienden el mismo arco, éstos son iguales. =b=g

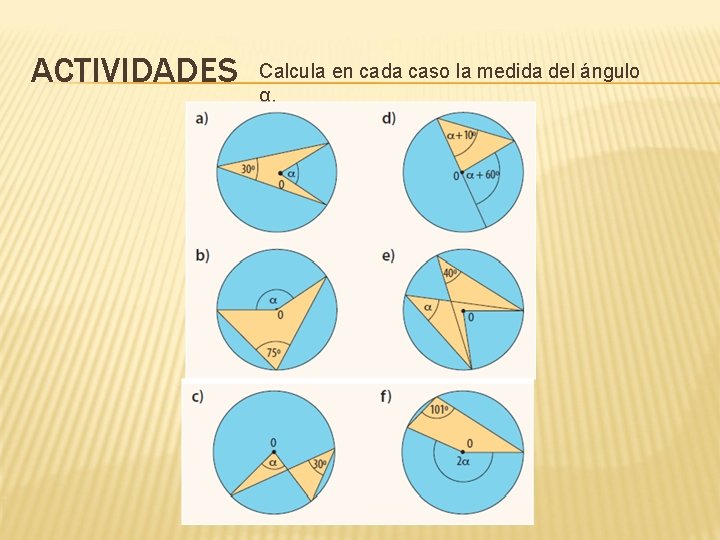
ACTIVIDADES Calcula en cada caso la medida del ángulo α.

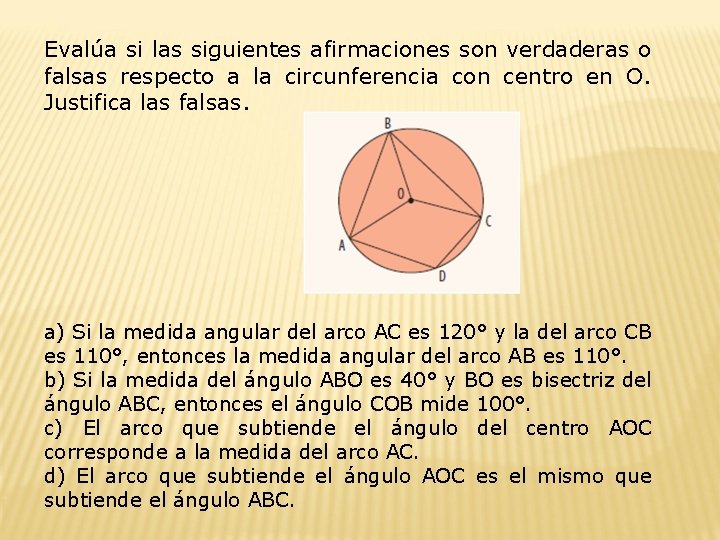
Evalúa si las siguientes afirmaciones son verdaderas o falsas respecto a la circunferencia con centro en O. Justifica las falsas. a) Si la medida angular del arco AC es 120° y la del arco CB es 110°, entonces la medida angular del arco AB es 110°. b) Si la medida del ángulo ABO es 40° y BO es bisectriz del ángulo ABC, entonces el ángulo COB mide 100°. c) El arco que subtiende el ángulo del centro AOC corresponde a la medida del arco AC. d) El arco que subtiende el ángulo AOC es el mismo que subtiende el ángulo ABC.

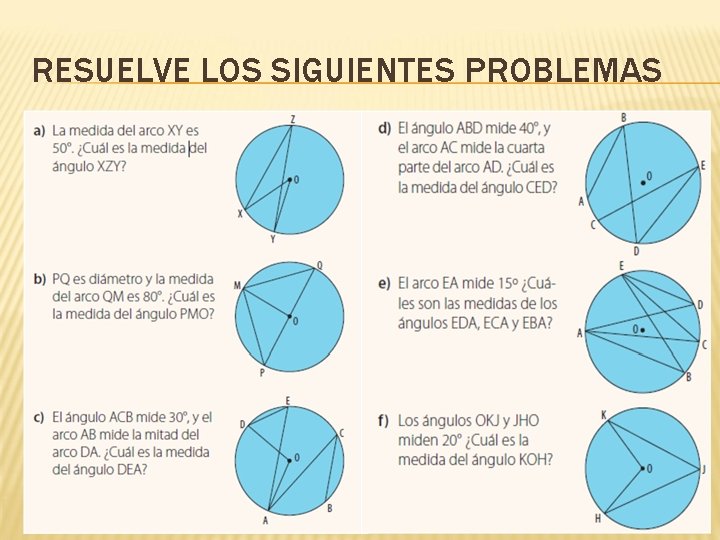
RESUELVE LOS SIGUIENTES PROBLEMAS

1. 3 Triángulo inscrito en una semicircunferencia Todo triángulo inscrito en una semicircunferencia es rectángulo con hipotenusa igual al diámetro. 180° O: centro de la circunferencia

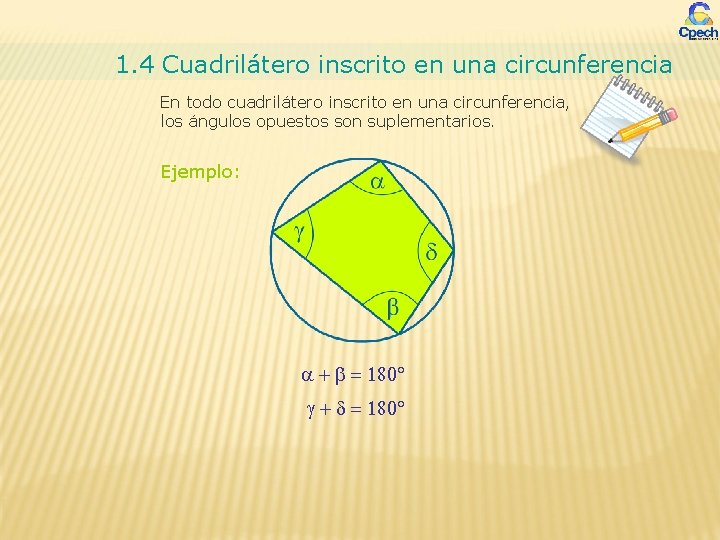
1. 4 Cuadrilátero inscrito en una circunferencia En todo cuadrilátero inscrito en una circunferencia, los ángulos opuestos son suplementarios. Ejemplo: + b = 180° g + d = 180°

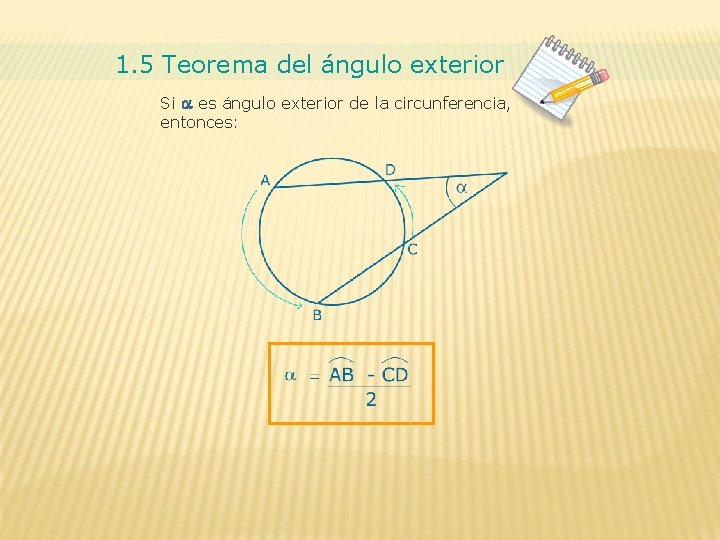
1. 5 Teorema del ángulo exterior Si a es ángulo exterior de la circunferencia, entonces:

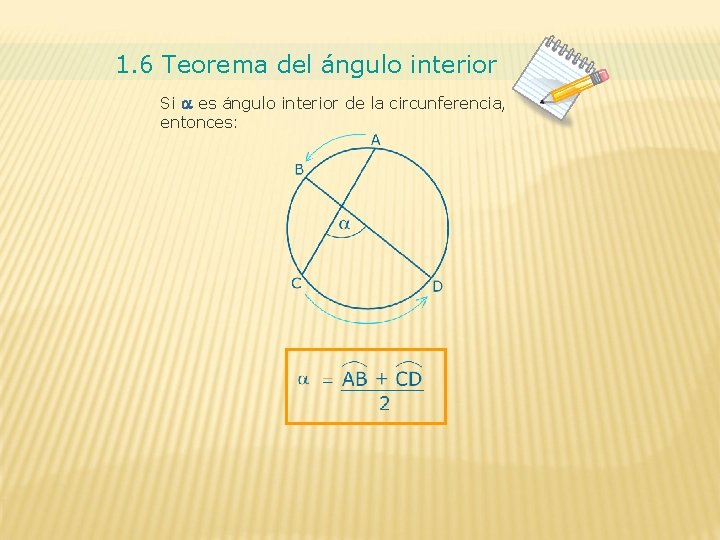
1. 6 Teorema del ángulo interior Si a es ángulo interior de la circunferencia, entonces:

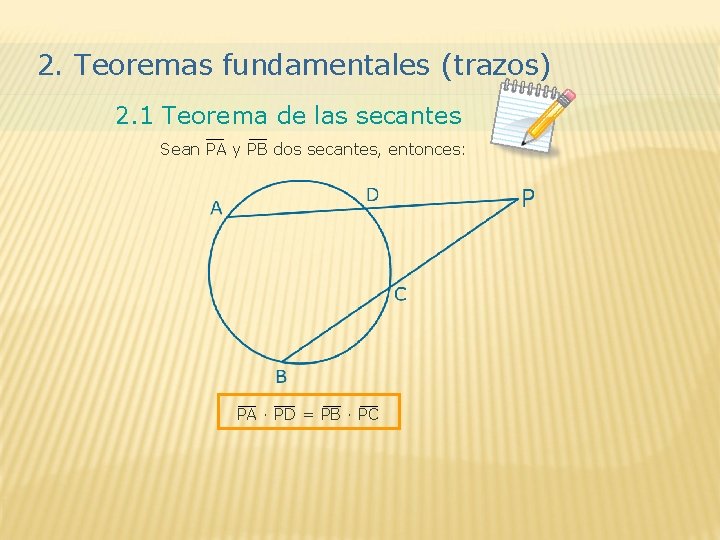
2. Teoremas fundamentales (trazos) 2. 1 Teorema de las secantes Sean PA y PB dos secantes, entonces: PA ∙ PD = PB ∙ PC

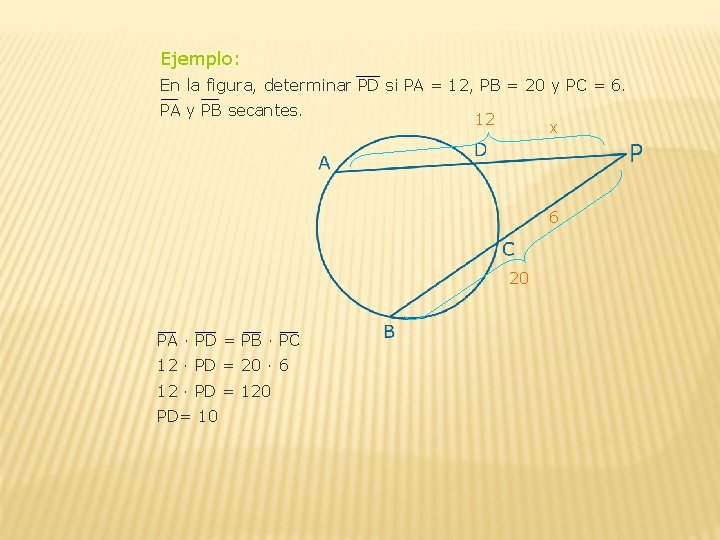
Ejemplo: En la figura, determinar PD si PA = 12, PB = 20 y PC = 6. PA y PB secantes. 12 x 6 20 PA ∙ PD = PB ∙ PC 12 ∙ PD = 20 ∙ 6 12 ∙ PD = 120 PD= 10

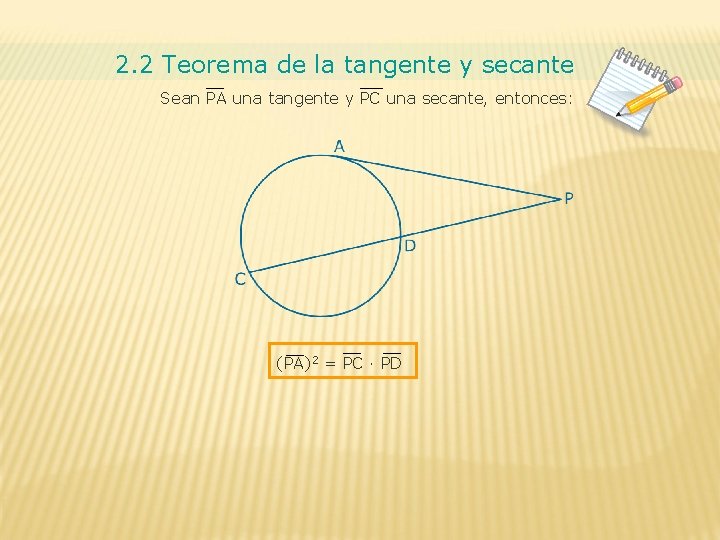
2. 2 Teorema de la tangente y secante Sean PA una tangente y PC una secante, entonces: (PA)2 = PC ∙ PD

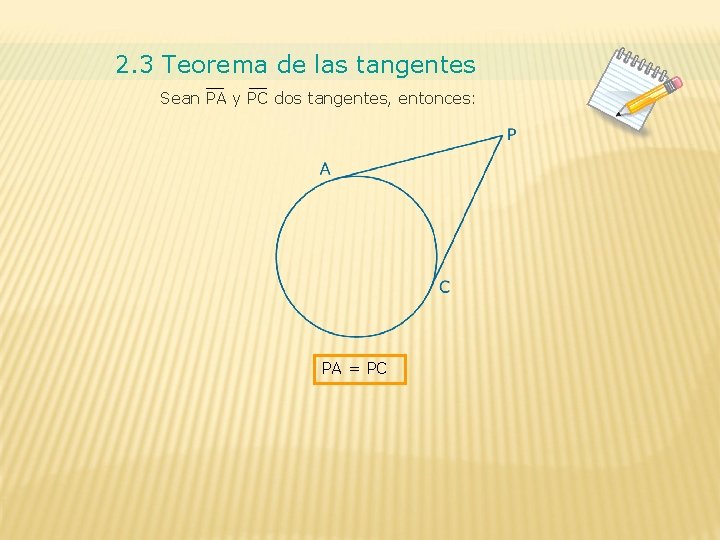
2. 3 Teorema de las tangentes Sean PA y PC dos tangentes, entonces: PA = PC

2. 4 Teorema de las cuerdas Sean AB y CD dos cuerdas, entonces: AP ∙ PB = CP ∙ PD

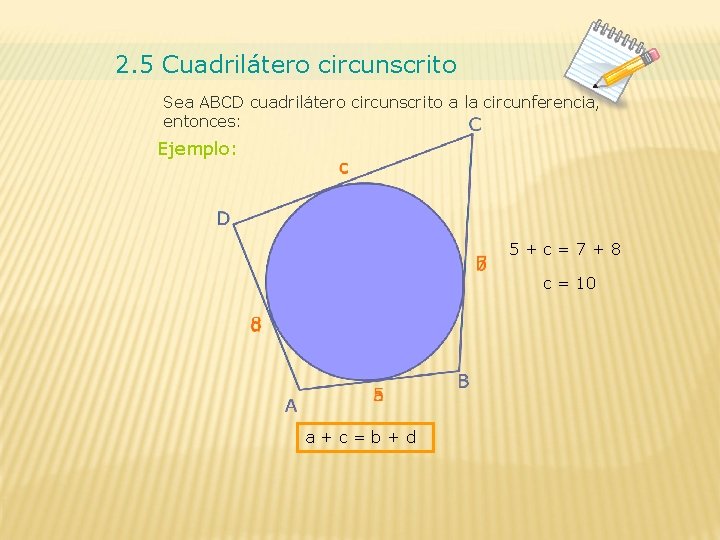
2. 5 Cuadrilátero circunscrito Sea ABCD cuadrilátero circunscrito a la circunferencia, entonces: Ejemplo: 5+c=7+8 c = 10 a+c=b+d

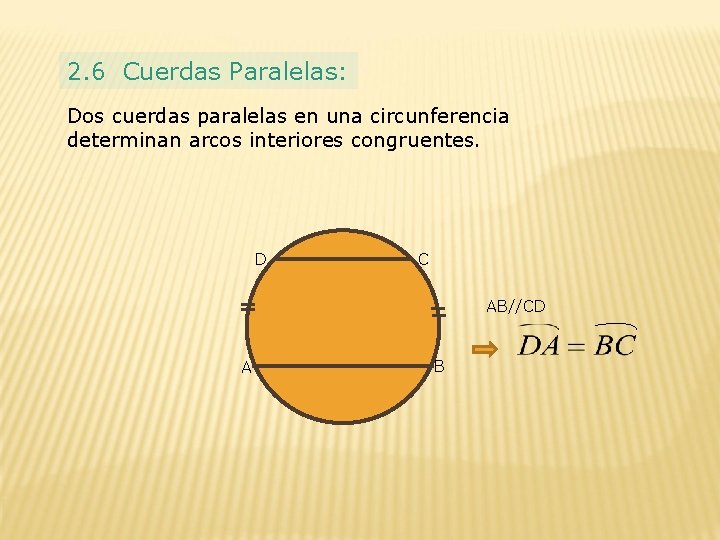
2. 6 Cuerdas Paralelas: Dos cuerdas paralelas en una circunferencia determinan arcos interiores congruentes. D C AB//CD A B



ACTIVIDADES Desarrolla las actividades de las páginas 136, 137, 138, 139, 141, 142, 143, 146 y 147 de tu texto.
 Circunferencias
Circunferencias La circunferencia de un círculo
La circunferencia de un círculo Semiretas
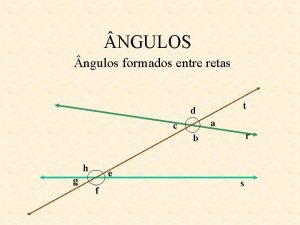
Semiretas Ngulo obtuso
Ngulo obtuso Ngulos
Ngulos Cuántos ángulos de 90 hay en un círculo
Cuántos ángulos de 90 hay en un círculo Ngulos
Ngulos Triangulo congruente
Triangulo congruente Condição de existencia de um triangulo
Condição de existencia de um triangulo Angulo consecutivo e adjacente
Angulo consecutivo e adjacente Retas coplanares
Retas coplanares Julia y maria caminan juntas llegan a un cruce de caminos
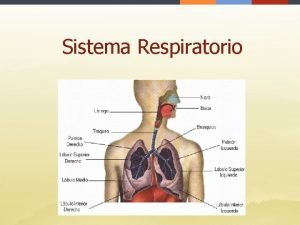
Julia y maria caminan juntas llegan a un cruce de caminos Comisura anterior laringe
Comisura anterior laringe Dcl
Dcl Musculos pectineos
Musculos pectineos Jorge martn
Jorge martn Pliegues vocales
Pliegues vocales Functions of trachea
Functions of trachea Epicardio endocardio y miocardio
Epicardio endocardio y miocardio Bronquios segmentarios
Bronquios segmentarios Familia de instrumentos de cuerda
Familia de instrumentos de cuerda Instrumento pastoril
Instrumento pastoril Cuerdas nudos e izamiento de material
Cuerdas nudos e izamiento de material Cuerdas de rescate vertical
Cuerdas de rescate vertical Musculos que sostienen las cuerdas tendinosas
Musculos que sostienen las cuerdas tendinosas La familia de cuerdas
La familia de cuerdas Teoremas de las circunferencias
Teoremas de las circunferencias Cuantos rectangulos hay
Cuantos rectangulos hay Circulo de mohr
Circulo de mohr Circulo hermeneutico dilthey
Circulo hermeneutico dilthey Area de un trapecio circular
Area de un trapecio circular Falacias argumentativas
Falacias argumentativas Circulo cromatico 12 colores
Circulo cromatico 12 colores Circulo unitario en radianes
Circulo unitario en radianes Circulo de fogo pacifico
Circulo de fogo pacifico Circulo de monteros
Circulo de monteros Paralelos sociales
Paralelos sociales Círculo con banda diametral
Círculo con banda diametral Sistancias acidas
Sistancias acidas Verecumdiam
Verecumdiam Uece suponha que o carbono assinalado com um circulo
Uece suponha que o carbono assinalado com um circulo Circulo vicioso de la desnutricion
Circulo vicioso de la desnutricion Circulo de mohr
Circulo de mohr