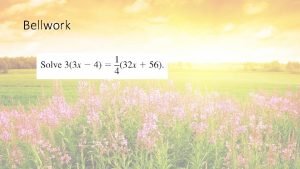Chapter 9 Properties of Transformations Translate Figures and

Chapter 9 Properties of Transformations

Translate Figures and Use Vectors �Translation: � moves every point of a figure the same distance in the same direction �Image: �the new figure formed by the translation �Preimage: �another name for the original figure �Isometry: �a transformation that preserves length and angle measurements

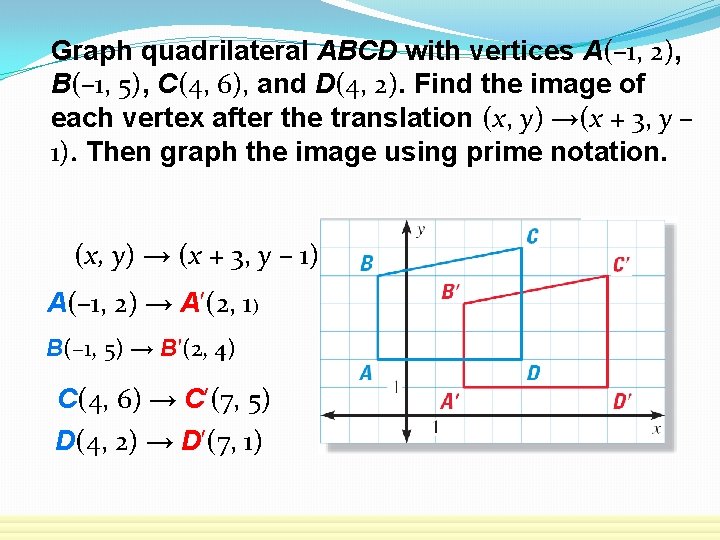
Graph quadrilateral ABCD with vertices A(– 1, 2), B(– 1, 5), C(4, 6), and D(4, 2). Find the image of each vertex after the translation (x, y) →(x + 3, y – 1). Then graph the image using prime notation. SOLUTION First, draw ABCD. Find the translation of each vertex by adding 3 to its x-coordinate and subtracting 1 from its y-coordinate. Then graph the image.

Graph quadrilateral ABCD with vertices A(– 1, 2), B(– 1, 5), C(4, 6), and D(4, 2). Find the image of each vertex after the translation (x, y) →(x + 3, y – 1). Then graph the image using prime notation. (x, y) → (x + 3, y – 1) A(– 1, 2) → A′(2, 1) B(– 1, 5) → B′(2, 4) C(4, 6) → C′(7, 5) D(4, 2) → D′(7, 1)

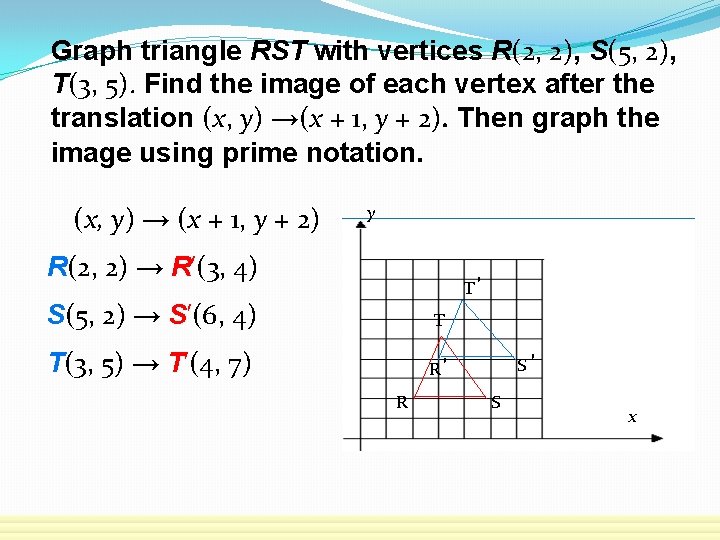
Draw RST with vertices R(2, 2), S(5, 2), and T(3, 5). Find the image of each vertex after the translation (x, y) → (x + 1, y + 2). Graph the image using prime notation. SOLUTION First, draw RST. Find the translation of each vertex by adding 1 to its x-coordinate and adding 2 to its y-coordinate. Then graph the image.

Graph triangle RST with vertices R(2, 2), S(5, 2), T(3, 5). Find the image of each vertex after the translation (x, y) →(x + 1, y + 2). Then graph the image using prime notation. (x, y) → (x + 1, y + 2) y R(2, 2) → R′(3, 4) T′ S(5, 2) → S′(6, 4) T T(3, 5) → T′(4, 7) R′ R S′ S x

The image of (x, y) → (x + 4, y – 7) is P′Q′ with endpoints P′(– 3, 4) and Q′(2, 1). Find the coordinates of the endpoints of the preimage. SOLUTION P'( - 3, 4) → P(– 7, 11) Q'(2, 1) → Q(– 2, 8)

Write a rule for the translation of ABC to A′B′C′. Then verify that the transformation is an isometry.

SOLUTION To go from A to A′, move 4 units left and 1 unit up. So, a rule for the translation is (x, y) →(x – 4, y + 1).

�Vectors: �a quantity that has both direction and magnitude and is represented in the coordinate plane by an arrow drawn from one point to another. �Initial point: �the starting point of the vector �Terminal point: �the ending point of the vector

�Component form: � combines the horizontal and vertical components �Horizontal component goes left to right. �Vertical component goes up and down.

Name the vector and write its component form. SOLUTION The vector is BC. From initial point B to terminal point C, you move 9 units right and 2 units down. So, the component form is 9, – 2.

Name the vector and write its component form. SOLUTION The vector is ST. From initial point S to terminal point T, you move 8 units left and 0 units vertically. The component form is – 8, 0.

Name the vector and write its component form. SOLUTION The vector is TX. From initial point T to terminal point S, you move 0 units horizontally and 3 units up. The component form is 0, 3.

The vertices of ∆LMN are L(2, 2), M(5, 3), and N(9, 1). Translate ∆LMN using the vector – 2, 6. SOLUTION Find the translation of each vertex by subtracting 2 from its x-coordinate and adding 6 to its y-coordinate. (x, y) → (x – 2, y + 6) L(2, 2) → L′(0, 8) M(5, 3) → M′(3, 9) N(9, 1) → N′(7, 7)

Lesson – 9. 3 Perform Reflections Reflection: a transformation that uses a line like a mirror to reflect an image Line of reflection: a line that acts like a mirror to reflect an image.

The vertices of ABC are A(1, 3), B(5, 2), and C(2, 1). Graph the reflection of ABC described. In the line m : y = 1 SOLUTION Point A is 2 units above m, so A′ is 2 units below m at (1, – 1). Also, B′ is 1 unit below m at (5, 0). Because point C is on line m, you know that C = C′.

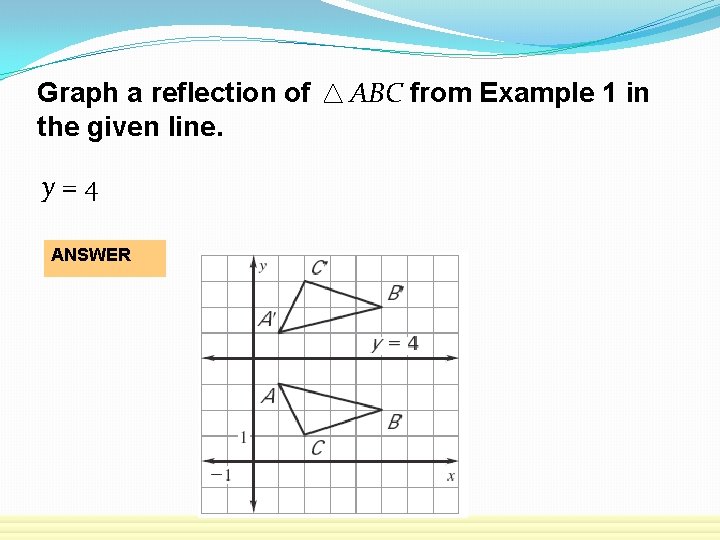
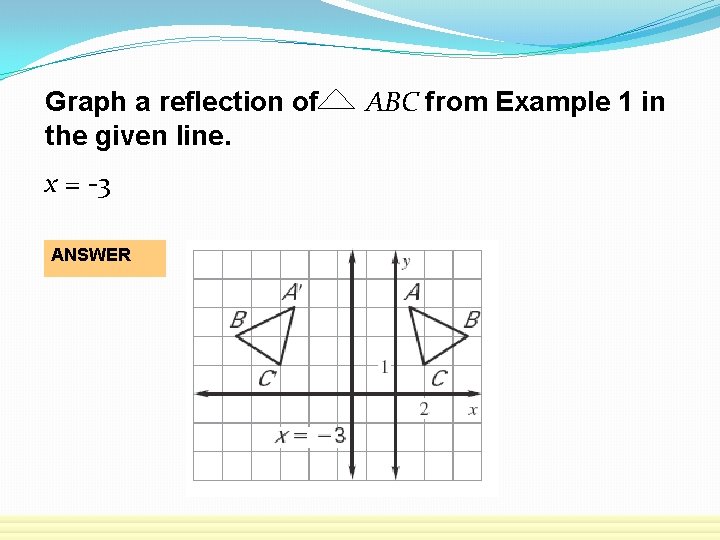
Graph a reflection of the given line. y=4 ANSWER ABC from Example 1 in

Graph a reflection of the given line. x = -3 ANSWER ABC from Example 1 in

Coordinate Rules for Reflections �If (a, b) is reflected in the x-axis, its image is the point � (a, -b). �If (a, b) is reflected in the y-axis, its image is the point � (-a, b). �If (a, b) is reflected in the line y = x, its image is the point �(b, a). �If (a, b) is reflected in the line y = - x, its image is the point �(-b, -a).

The endpoints of FG are F(– 1, 2) and G(1, 2). Reflect the segment in the line y = x. Graph the segment and its image.

SOLUTION The slope of y = x is 1. The segment from F to its image, FF ′ , is perpendicular to the line of reflection y = x, so the slope of FF ′ will be – 1 (because 1(– 1) = – 1). From F, move 1. 5 units right and 1. 5 units down to y = x. From that point, move 1. 5 units right and 1. 5 units down to locate F′(2, – 1). The slope of GG′ will also be – 1. From G, move 0. 5 units right and 0. 5 units down to y = x. Then move 0. 5 units right and 0. 5 units down to locate G′ (2, 1).

Reflect FG from Example 2 in the line y = –x. Graph FG and its image. SOLUTION Use the coordinate rule for reflecting in y = –x. (a, b) (–b, –a) F(– 1, 2) F ′ (– 2, 1) G(1, 2) G ′ (– 2, – 1)

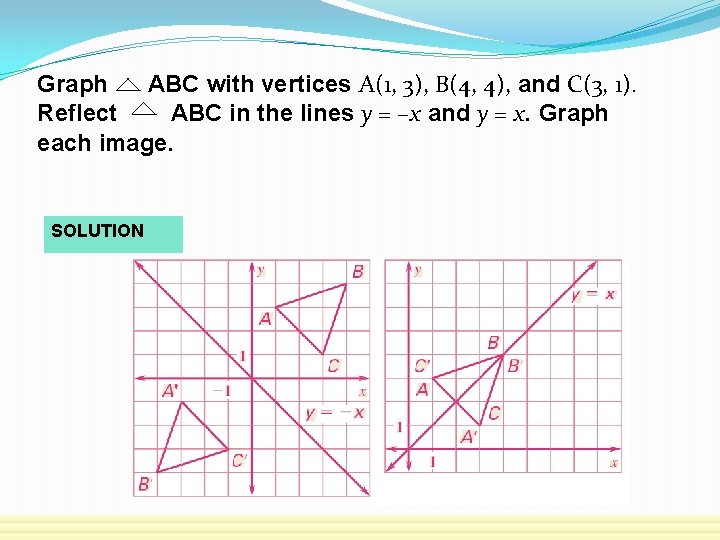
Graph ABC with vertices A(1, 3), B(4, 4), and C(3, 1). Reflect ABC in the lines y = –x and y = x. Graph each image. SOLUTION

� Homework: �p. 593 -595 {1 -12}

Lesson 9. 6 -Identify Symmetry �Line Symmetry: �occurs in a figure in a plane if the figure can be mapped onto itself by a reflection in a line. �Line of Symmetry: �The line of reflection that maps a figure onto itself �Rotational symmetry: a figure that can be mapped onto itself by a rotation of or less about the center of the figure �

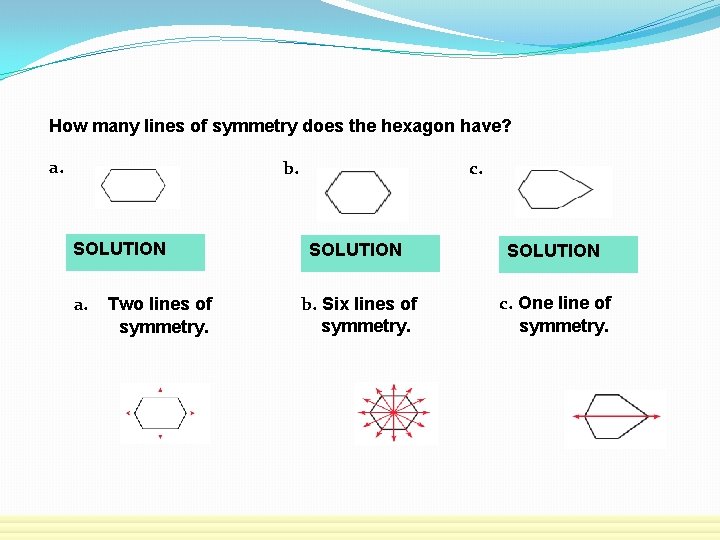
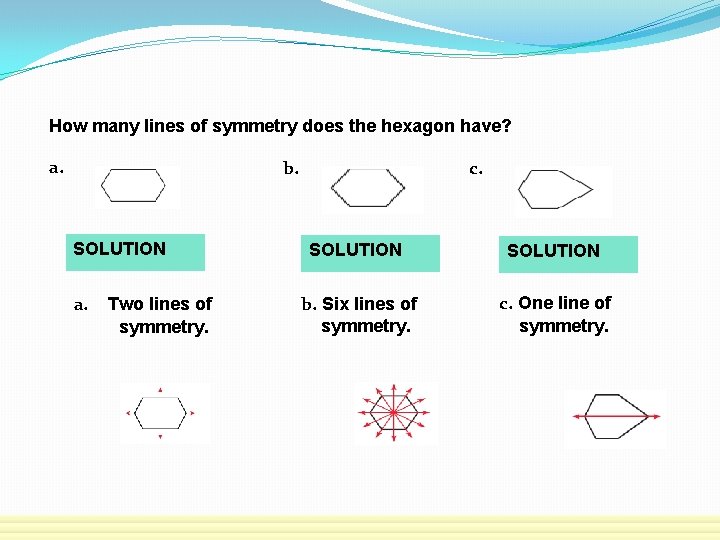
How many lines of symmetry does the hexagon have? a. c. b. SOLUTION a. Two lines of symmetry. SOLUTION b. Six lines of symmetry. c. One line of symmetry.

How many lines of symmetry does the object appear to have? 1. 2. ANSWER 8 3. ANSWER 5 ANSWER 1

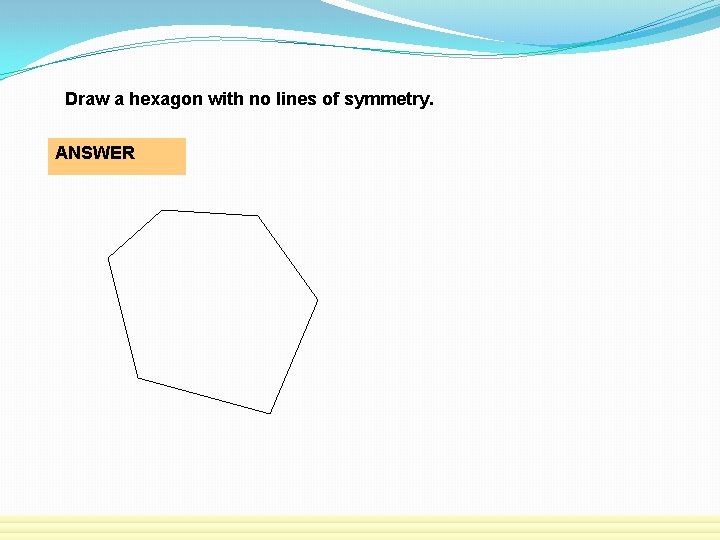
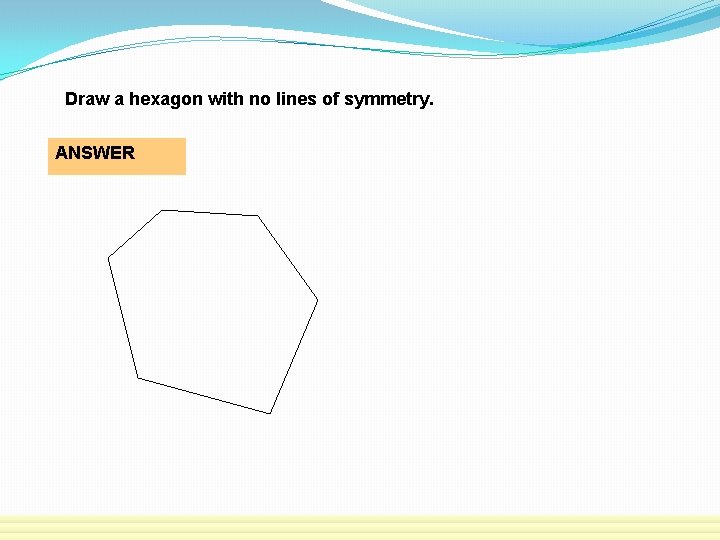
Draw a hexagon with no lines of symmetry. ANSWER

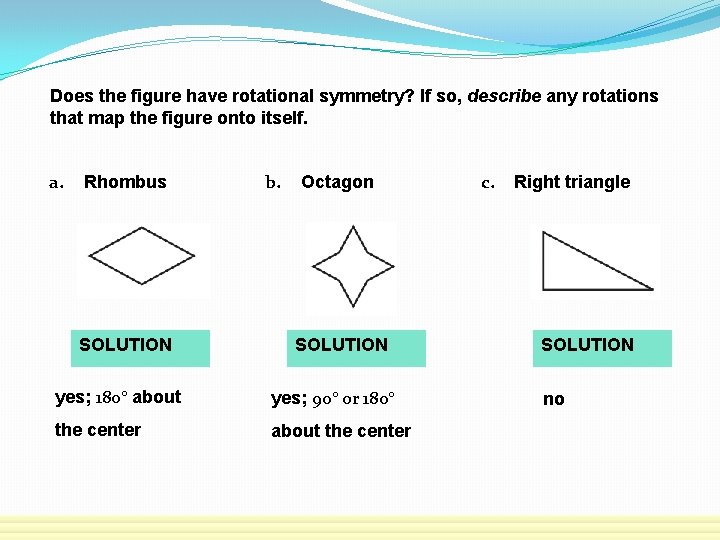
Does the figure have rotational symmetry? If so, describe any rotations that map the figure onto itself. a. Parallelogram SOLUTION a. The parallelogram has rotational symmetry. The center is the intersection of the diagonals. A 180° rotation about the center maps the parallelogram onto itself.

b. Regular octagon SOLUTION b. The regular octagon has rotational symmetry. The center is the intersection of the diagonals. Rotations of 45 , 90 , 135 , or 180° about the center all map the octagon onto itself. o o o

c. Trapezoid SOLUTION c. The trapezoid does not have rotational symmetry because no rotation of 180° or less maps the trapezoid onto itself.

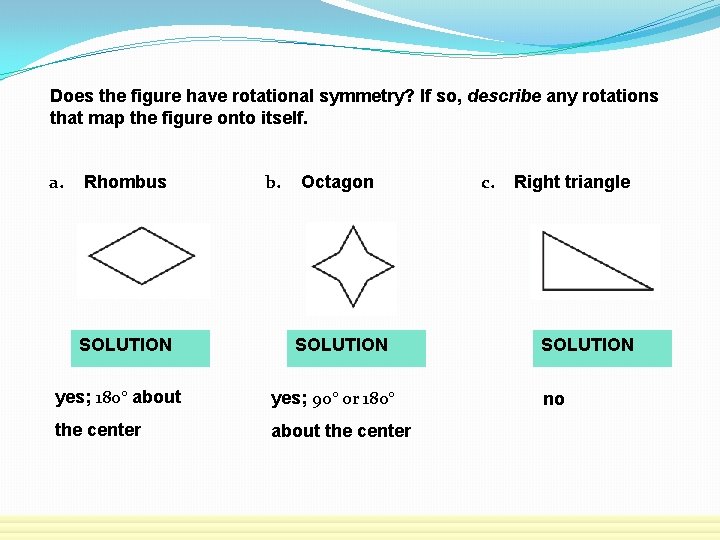
Does the figure have rotational symmetry? If so, describe any rotations that map the figure onto itself. a. Rhombus SOLUTION b. Octagon SOLUTION yes; 180° about yes; 90° or 180° the center about the center c. Right triangle SOLUTION no

Homework: p 621: {3 -5, 6, 13, 14, 17, 18}

Section 9. 4 – Perform Rotations Rotation: a transformation in which a figure is turned about a fixed point Center of Rotation: the fixed point in which a figure is turned about Angle of Rotation: formed from rays drawn from the center of rotation to a point and its image.

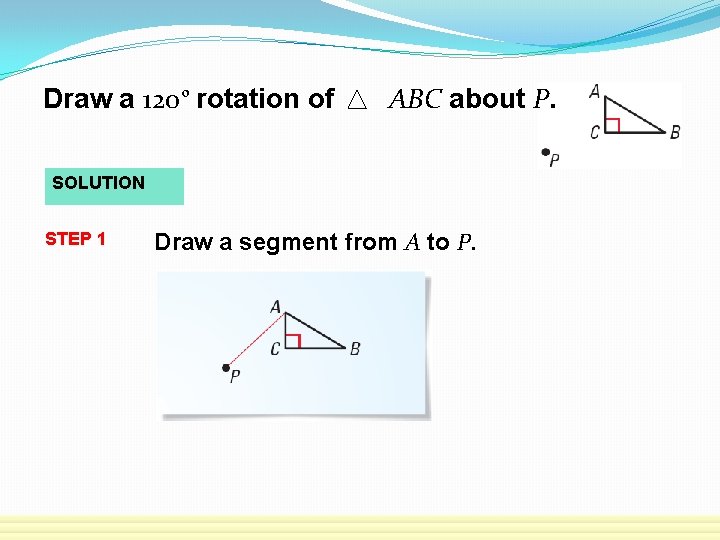
Draw a 120 o rotation of ABC about P. SOLUTION STEP 1 Draw a segment from A to P.

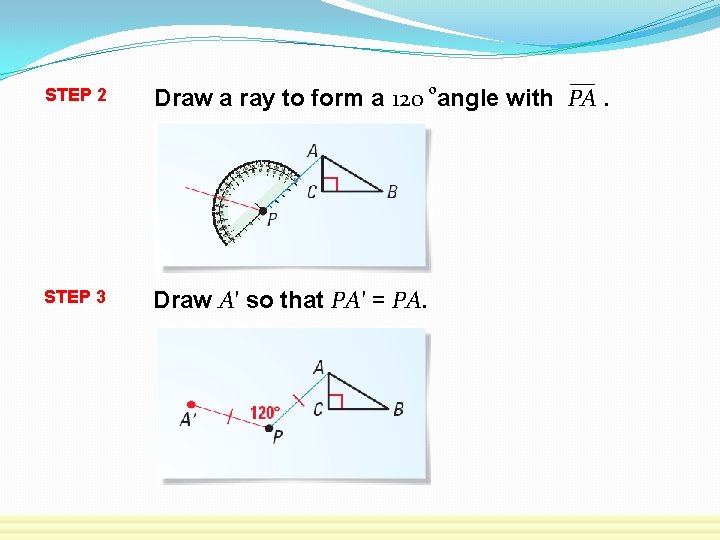
o STEP 2 Draw a ray to form a 120 angle with PA. STEP 3 Draw A′ so that PA′ = PA.

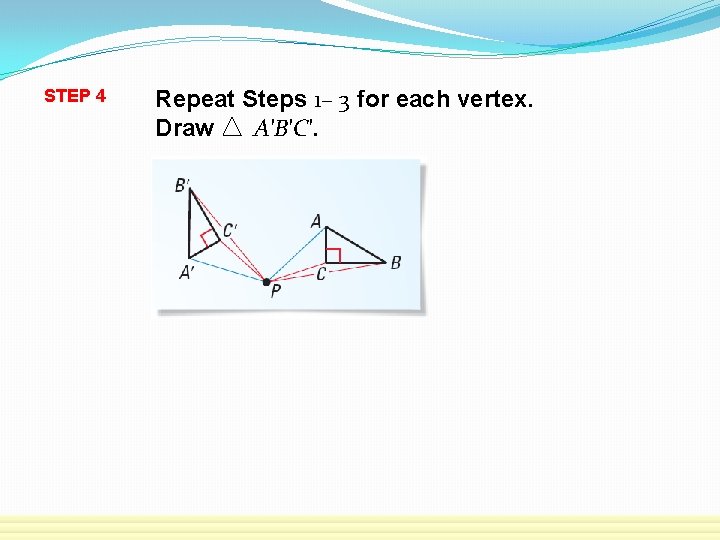
STEP 4 Repeat Steps 1– 3 for each vertex. Draw A′B′C′.

Coordinate Rules for Rotations about the origin �When a point (a, b) is rotated counterclockwise about the origin, the following are true: � 1. For a rotation of 90 , (a, b) becomes (-b, a). � 2. For a rotation of 180 , (a, b) becomes (-a, -b). � 3. For a rotation of 270 , (a, b) becomes (b, -a).

Graph quadrilateral RSTU with vertices R(3, 1), S(5, 1), o T(5, – 3), and U(2, – 1). Then rotate the quadrilateral 270 about the origin. SOLUTION o Graph RSTU. Use the coordinate rule for a 270 rotation to find the images of the vertices. (a, b) (b, –a) R′(1, – 3) R(3, 1) S(5, 1) S′(1, – 5) T(5, – 3) T′(– 3, – 5) U(2, – 1) U′(– 1, – 2) Graph the image R′S′T′U′.

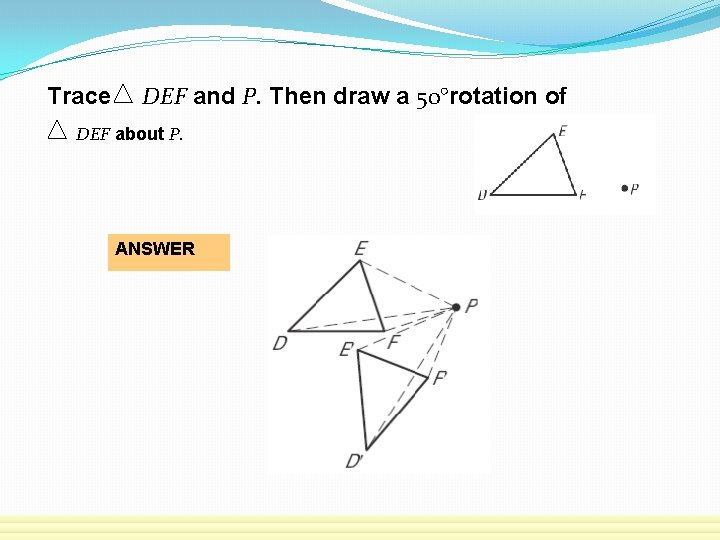
Trace DEF and P. Then draw a 50°rotation of DEF about P. ANSWER

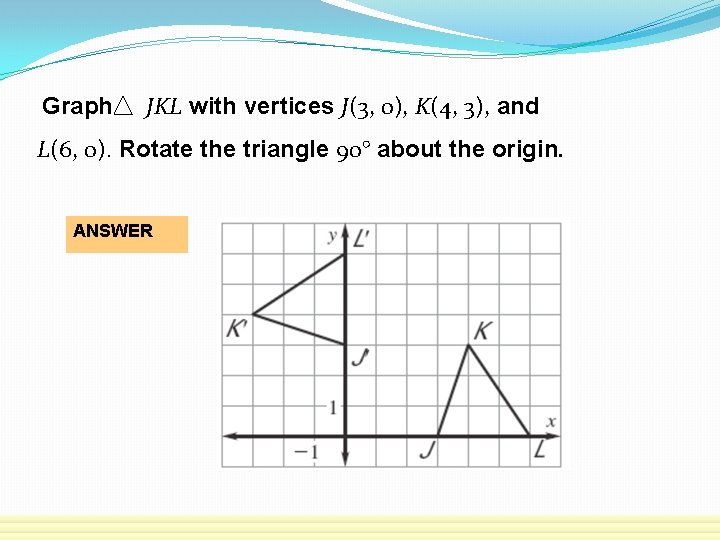
Graph JKL with vertices J(3, 0), K(4, 3), and L(6, 0). Rotate the triangle 90° about the origin. ANSWER

SOLUTION By Theorem 9. 3, the rotation is an isometry, so corresponding side lengths are equal. Then 2 x = 6, so x = 3. Now set up an equation to solve for y. 5 y = 3 x + 1 5 y = 3(3) + 1 y Substitute 3 for x. Corresponding lengths in an isometry are equal. Solve for y. = 2 The correct answer is B.

Find the value of r in the rotation of the triangle. ANSWER The correct answer is B.

HOMEWORK: p. 602 -603 {1, 3 -14, 20, 21, 23

TESSELLATIO NS HOW TO DO IT YOURSELF! SLICE METHOD

�Slice Method - Example 1 �First a very simple one to show the principle. 1. Start with a shape that is known to tessellate - in this case, a square. . .

�Slice Method - Example 1 � 2. Mark out a shape to be cut on one side. . .

�Slice Method - Example 1 � 3. Cut out the slice and place it on the opposite side. . .

�Slice Method - Example 1 � 4. This shape will tessellate like this. . .

�Slice Method - Example 1 � 5. And it's possible to make a simple picture with it. It will still tessellate if the piece is reversed or stuck on the side. It will even do so if a piece is taken from the side and the top together. . . there are several combinations but some will not work.

Slice Method - Example 2 Begin with a shape that will tessellate. This is a hexagon with opposite sides equal. Such a shape is always OK. . .

Slice Method - Example 2 2. Draw a random squiggly line along one side making sure it ends at the corners. . .

Slice Method - Example 2 3. Cut out the slice and paste it along the outside of the opposite side. . .

Slice Method - Example 2 4. Draw a random line on another side. . .

Slice Method - Example 2 5. Cut the slice out and paste it on the opposite side as before. . .

Slice Method - Example 2 6. Repeat for the remaining side. . .

Slice Method - Example 2 7. Look at the resulting shape - any ideas yet?

Slice Method - Example 2 8. To give a clean shape, remove all the bits outside the lines and fill in the corresponding parts inside. What is it?

Slice Method - Example 2 9. This is what I saw! As you see, the shape was arrived at quite by accident but I acknowledge the Disney copyright of my artistic filling in. Will it tessellate?

Slice Method - Example 2 10. Yes, of course! Can we improve it?

Slice Method - Example 2 11. Add a road, wall and pavement and we have a parade!

YOUR TURN! GOOD LUCK!!!

Section 9. 5: Apply Compositions of ransformations Glide Reflection: A transformation in which every point P is mapped to a point P” by the following steps. 1. a translation maps P to P’ 2. a reflection in a line k parallel to the direction of the translation maps P’ to P”

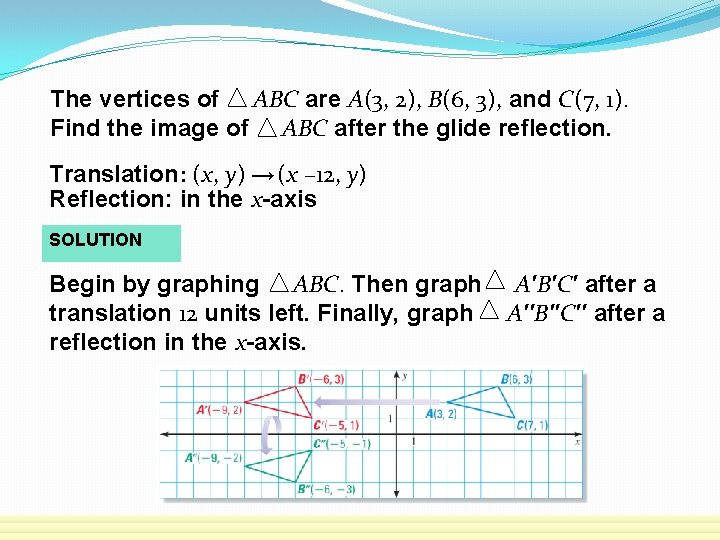
The vertices of ABC are A(3, 2), B(6, 3), and C(7, 1). Find the image of ABC after the glide reflection. Translation: (x, y) → (x – 12, y) Reflection: in the x-axis SOLUTION Begin by graphing ABC. Then graph translation 12 units left. Finally, graph reflection in the x-axis. A′B′C′ after a A′′B′′C′′ after a

Suppose ABC in Example 1 is translated 4 units down, then reflected in the y-axis. What are the coordinates of the vertices of the image? SOLUTION Translation: (x, y) (x , y – 4 ) Reflection: in the y-axis (x, y) → (–a, b) (x, y) (x , y – 4 ) → (–a, b) A(3, 2) → A′(3, – 2) → A"(– 3, – 2) B(6, 3) → B′(6, – 1) → B"(– 6, – 1) C(7, 1) → C′(7, – 3) → C"(– 7, – 3)

In Example 1, describe a glide reflection from A′′B′′C′′ to ABC. SOLUTION Translation: (x, y) → (x +12, y) Reflection: in the x-axis Begin by graphing A′B′C′. Then graph translation 12 units right. Finally, graph reflection in the x-axis. ABC after a

�Composition of Transformations: �the result of two or more transformations that are combined to form a single transformation

The endpoints of RS are R(1, – 3) and S(2, – 6). Graph the image of RS after the composition. Reflection: in the y-axis Rotation: 90° about the origin SOLUTION STEP 1 Graph RS STEP 2 Reflect RS in the y-axis. R′S′ has endpoints R′(– 1, – 3) and S′(– 2, – 6).

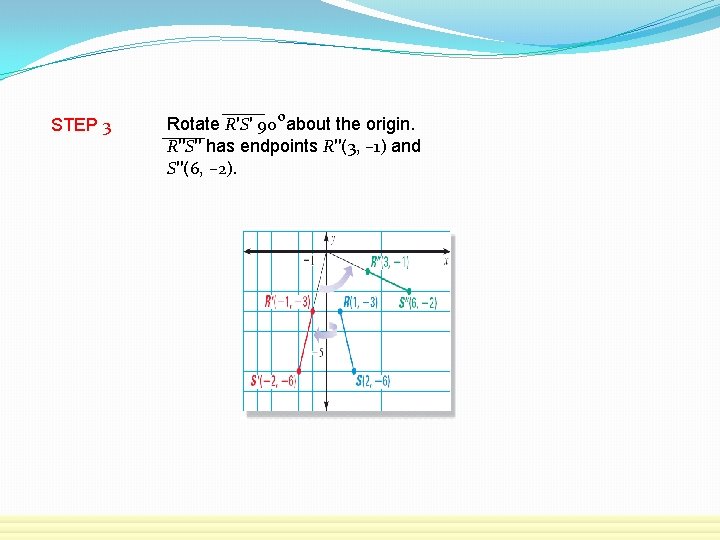
STEP 3 o Rotate R′S′ 90 about the origin. R′′S′′ has endpoints R′′(3, – 1) and S′′(6, – 2).

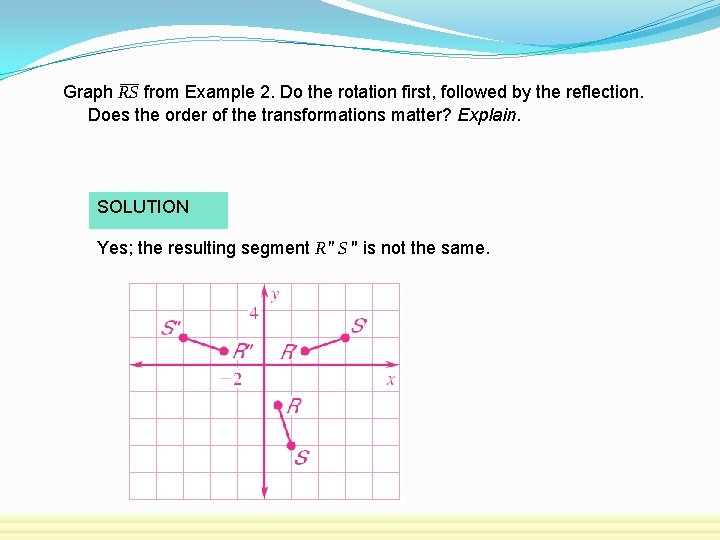
Graph RS from Example 2. Do the rotation first, followed by the reflection. Does the order of the transformations matter? Explain. SOLUTION Yes; the resulting segment R′′ S ′′ is not the same.

HOMEWORK �p. 602 -603 {1 , 3 -14, 20, 21, 23} �p. 611 -612 {1 -4, 7, 9, 11, 13, 14}

Lesson 9. 6 -Identify Symmetry �Line Symmetry occurs in a figure in a plane if the figure can be mapped onto itself by a reflection in a line. �Line of Symmetry: �The line of reflection that maps a figure onto itself �Rotational symmetry: a figure that can be mapped onto itself by a rotation of or less about the center of the figure �

How many lines of symmetry does the hexagon have? a. b. SOLUTION a. Two lines of symmetry. c. SOLUTION b. Six lines of symmetry. c. One line of symmetry.

How many lines of symmetry does the object appear to have? 1. 2. ANSWER 8 3. ANSWER 5 ANSWER 1

Draw a hexagon with no lines of symmetry. ANSWER

Does the figure have rotational symmetry? If so, describe any rotations that map the figure onto itself. a. Parallelogram SOLUTION a. The parallelogram has rotational symmetry. The center is the intersection of the diagonals. A 180° rotation about the center maps the parallelogram onto itself.

b. Regular octagon SOLUTION b. The regular octagon has rotational symmetry. The center is the intersection of the diagonals. Rotations of 45 , 90 , 135 , or 180° about the center all map the octagon onto itself. o o o

c. Trapezoid SOLUTION c. The trapezoid does not have rotational symmetry because no rotation of 180° or less maps the trapezoid onto itself.

Does the figure have rotational symmetry? If so, describe any rotations that map the figure onto itself. a. Rhombus SOLUTION b. Octagon SOLUTION yes; 180° about yes; 90° or 180° the center about the center c. Right triangle SOLUTION no

Homework: p 621: {3 -5, 6, 13, 14, 17, 18}

Lesson 9. 7 Identify and Perform Dilations �Dilation: a transformation that stretches or shrinks a figure to create a similar figure. �Center of Dilation: the fixed point �Scale Factor of a Dilation: the ratio of a side length of the image to the corresponding side length of the original figure.

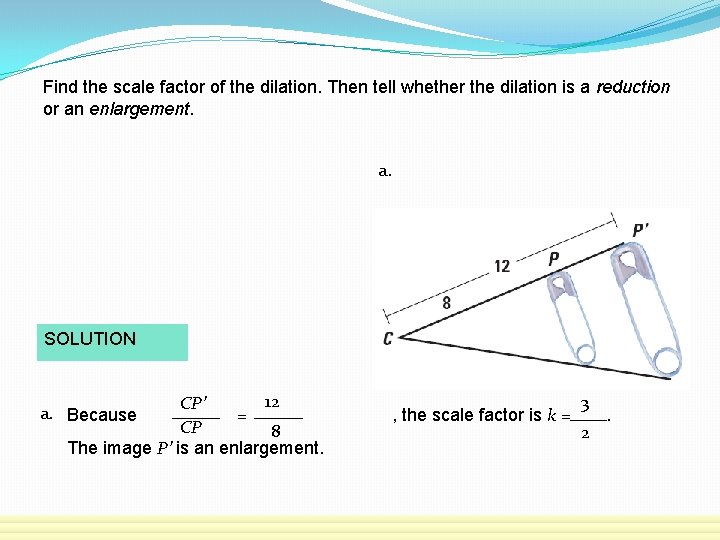
Find the scale factor of the dilation. Then tell whether the dilation is a reduction or an enlargement. a. SOLUTION 12 CP’ = CP 8 The image P’ is an enlargement. a. Because , the scale factor is k = 3 2 .

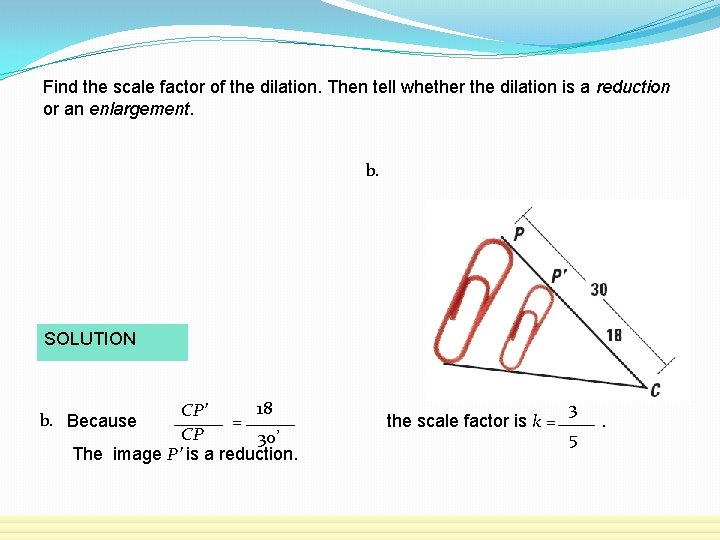
Find the scale factor of the dilation. Then tell whether the dilation is a reduction or an enlargement. b. SOLUTION 18 CP’ = CP 30’ The image P’ is a reduction. b. Because the scale factor is k = 3 5 .

Draw and label DEFG. Then construct a dilation of as the center of dilation and a scale factor of 2. DEFG with point D SOLUTION STEP 1 Draw DEFG. Draw rays from D through vertices E, F, and G.

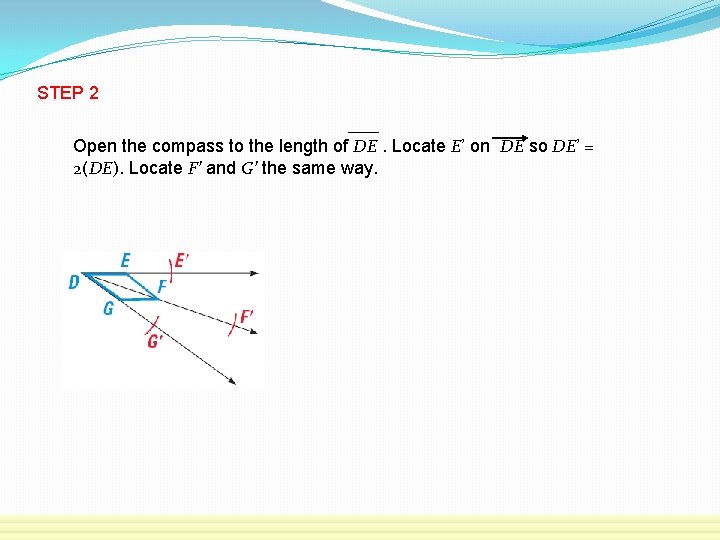
STEP 2 Open the compass to the length of DE. Locate E’ on DE so DE’ = 2(DE). Locate F’ and G’ the same way.

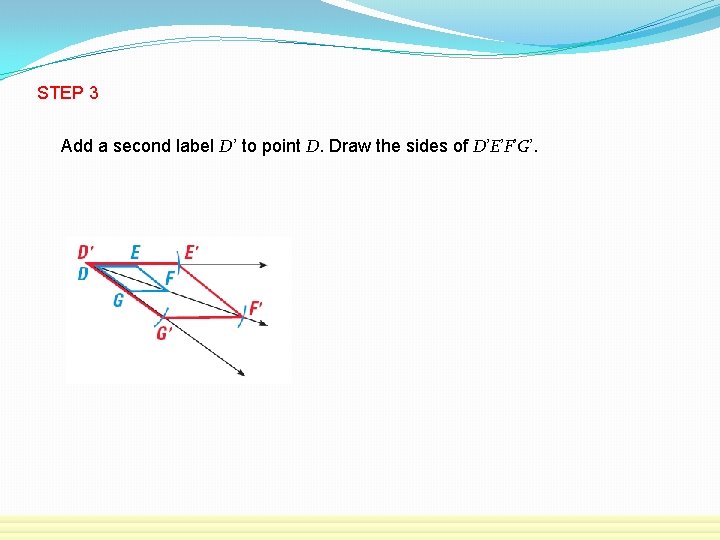
STEP 3 Add a second label D’ to point D. Draw the sides of D’E’F’G’.

In a dilation, CP’ = 3 and CP = 12. Tell whether the dilation is a reduction or an enlargement and find its scale factor. ANSWER 3 CP’ Because = CP 12 The image P’ is a reduction. , the scale factor is k = 1 4 .

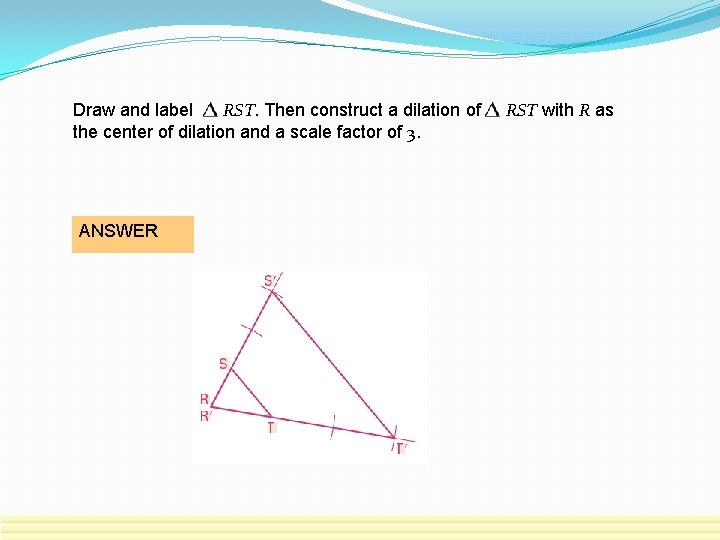
Draw and label RST. Then construct a dilation of the center of dilation and a scale factor of 3. ANSWER RST with R as

Homework: �p. 629 - 630 {3 -5, 7, 11, 13, 21, 22, 23}