Similar and Congruent Figures z Similar figures have

z. The symbol ~ shapes are similar z. The symbol are congruent means that

Congruent Figures F B 12 8 E A C D What is the length

Similar Figures C A F FIGURE 1 G E B Figure 2 D Side

Congruent Triangles z. Congruent triangles have three congruent sides and three congruent angles. z.

The Triangle Congruence Postulates &Theorems FOR ALL TRIANGLES SSS SAS ASA AAS FOR RIGHT

Theorem z. If two angles in one triangle are congruent to two angles in

A closer look. . . z If two triangles have two pairs of angles

Example 30° Why aren’t these triangles congruent? What do we call these triangles?

z. So, how do we prove that two triangles really are congruent?

ASA (Angle, Side, Angle) A C D z. If two angles and the included

AAS (Angle, Side) Special case of ASA z If two angles and a nonincluded

SAS (Side, Angle, Side) A C D z. If in two triangles, two sides

SSS (Side, Side) A C B D F E z. In two triangles, if

HL (Hypotenuse, Leg) z If both hypotenuses and a pair of legs of two

HA (Hypotenuse, Angle) A z If both hypotenuses and a pair of acute angles

LA (Leg, Angle) A z If both hypotenuses and a pair of acute angles

LL (Leg, Leg) A z If both pair of legs of two RIGHT triangles

Example 1 A C B D E F z Given the markings on the

Example 2 A C B D E F z Given the markings on the

Example 3 A C B D z Given the markings on the diagram, is

D Example 4 z Why are the two triangles congruent? SAS F E A

Example 5 A z Why are the two triangles congruent? SSS D B z

Example 6 B C z. Given: A Are the triangles congruent? Why? S S

Example 7 Q P z. Given: T m QSR = m PRS = 90°

Summary: ASA - Pairs of congruent sides contained between two congruent angles AAS –

Summary --for Right Triangles Only: HL – Pair of sides including the Hypotenuse and

Slides: 30

Download presentation

Similar and Congruent Figures z. Similar figures have the same shape, but not the same size. They must have the same ratio of side lengths z. Congruent figures have the same shape and the same size z. Corresponding parts are the sides or angles that have the same position.

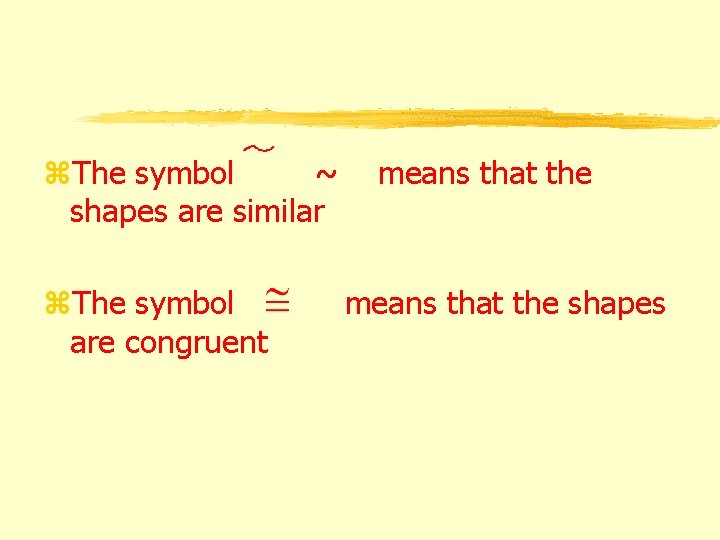
z. The symbol ~ shapes are similar z. The symbol are congruent means that the shapes

Similar Triangles

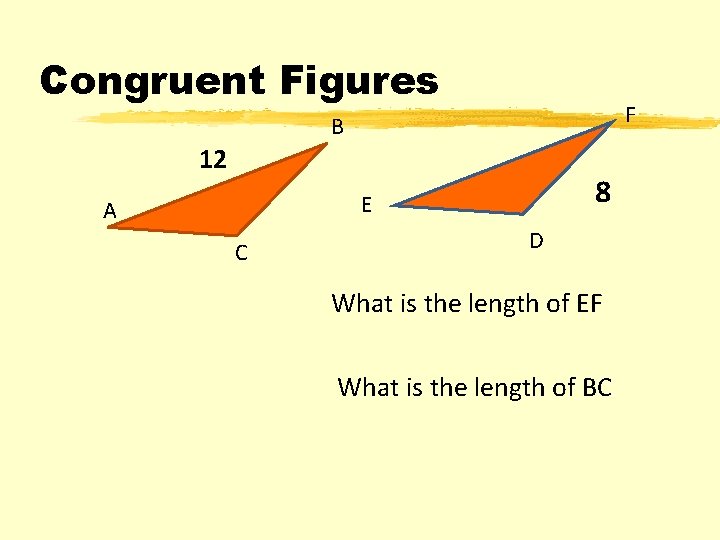
Congruent Figures F B 12 8 E A C D What is the length of EF What is the length of BC

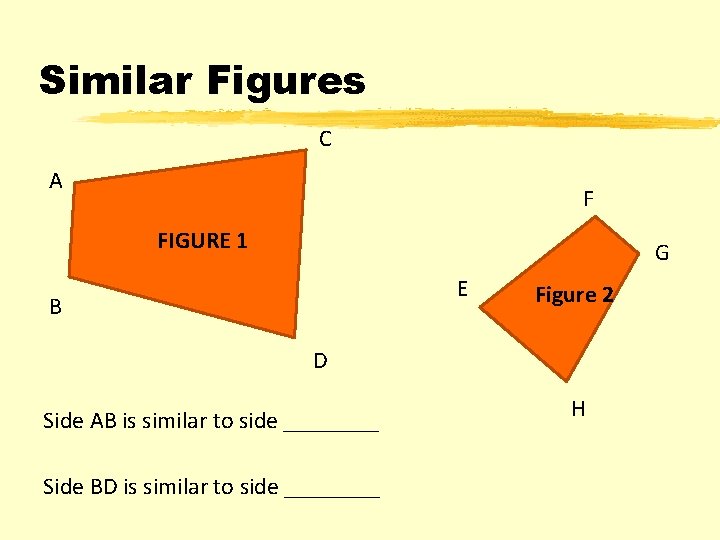
Similar Figures C A F FIGURE 1 G E B Figure 2 D Side AB is similar to side ____ Side BD is similar to side ____ H

Geometry Triangle Congruence Theorems

Congruent Triangles z. Congruent triangles have three congruent sides and three congruent angles. z. However, triangles can be proved congruent without showing 3 pairs of congruent sides and angles.

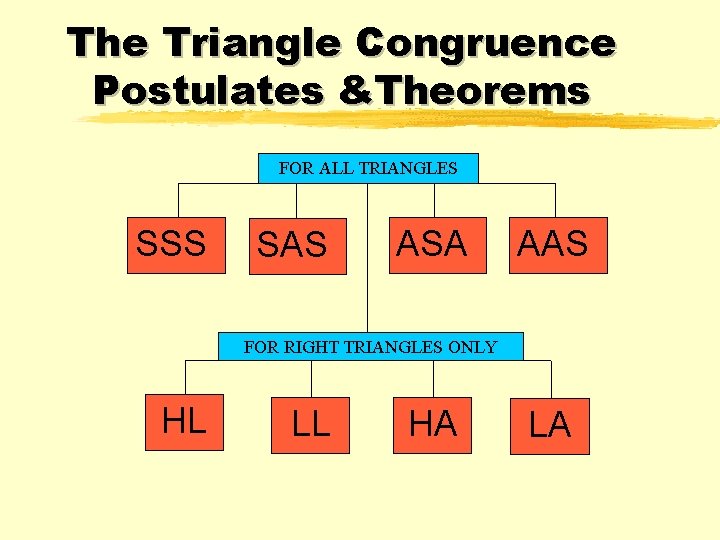
The Triangle Congruence Postulates &Theorems FOR ALL TRIANGLES SSS SAS ASA AAS FOR RIGHT TRIANGLES ONLY HL LL HA LA

Theorem z. If two angles in one triangle are congruent to two angles in another triangle, the third angles must also be congruent. z. Think about it… they have to add up to 180°.

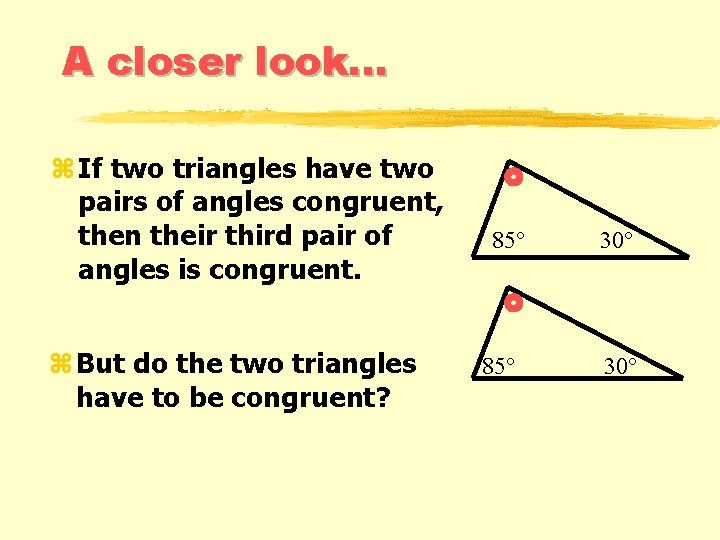
A closer look. . . z If two triangles have two pairs of angles congruent, then their third pair of angles is congruent. z But do the two triangles have to be congruent? 85° 30°

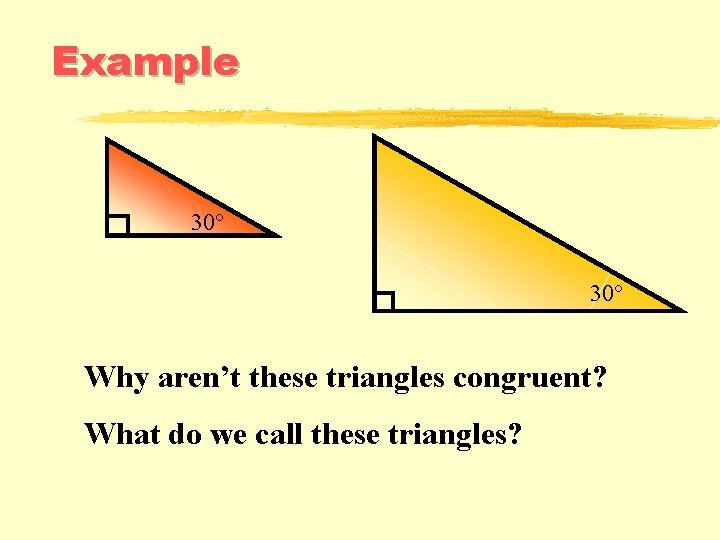
Example 30° Why aren’t these triangles congruent? What do we call these triangles?

z. So, how do we prove that two triangles really are congruent?

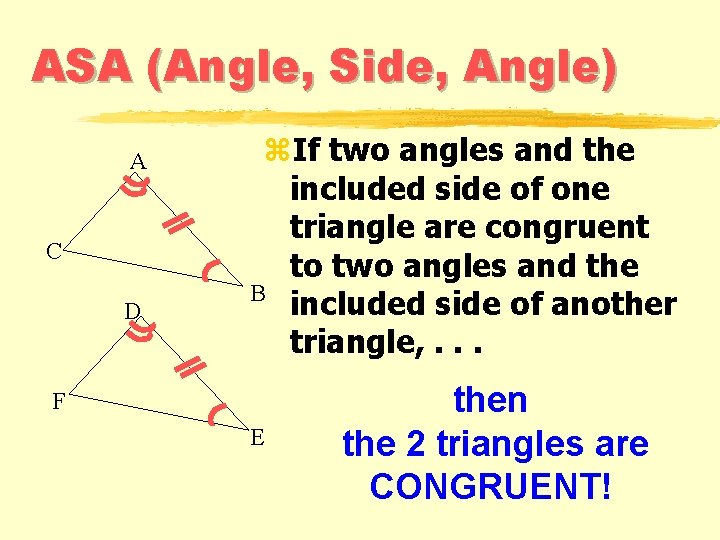
ASA (Angle, Side, Angle) A C D z. If two angles and the included side of one triangle are congruent to two angles and the B included side of another triangle, . . . F E then the 2 triangles are CONGRUENT!

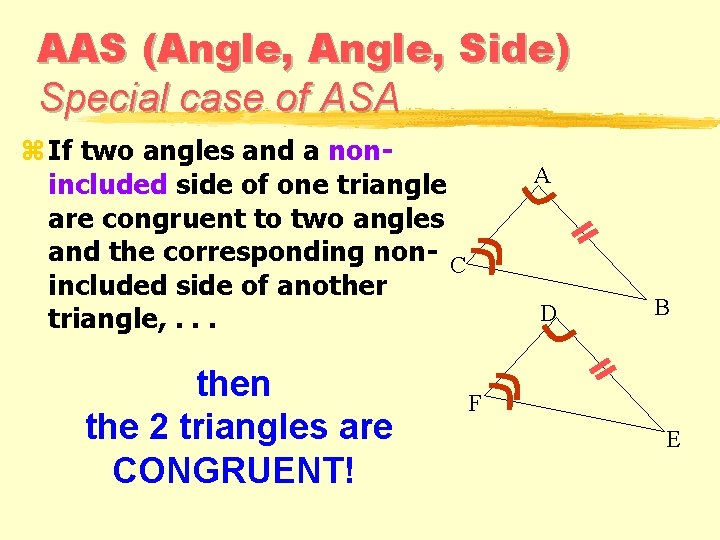
AAS (Angle, Side) Special case of ASA z If two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding non- C included side of another triangle, . . . then the 2 triangles are CONGRUENT! A D B F E

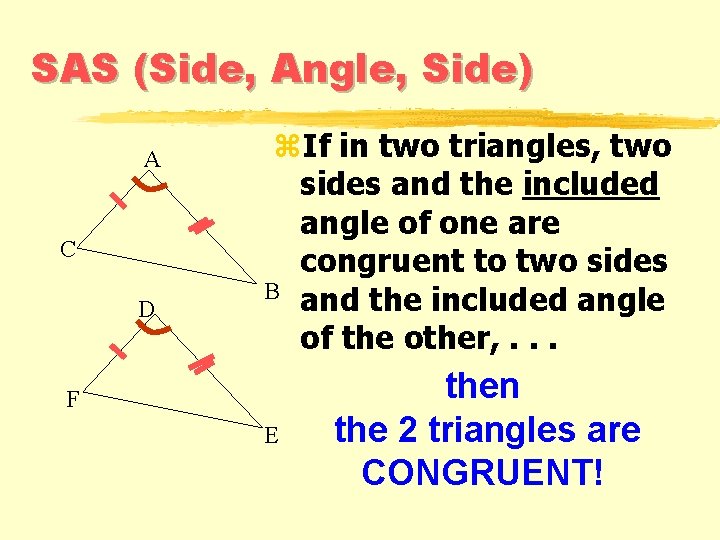
SAS (Side, Angle, Side) A C D z. If in two triangles, two sides and the included angle of one are congruent to two sides B and the included angle of the other, . . . F E then the 2 triangles are CONGRUENT!

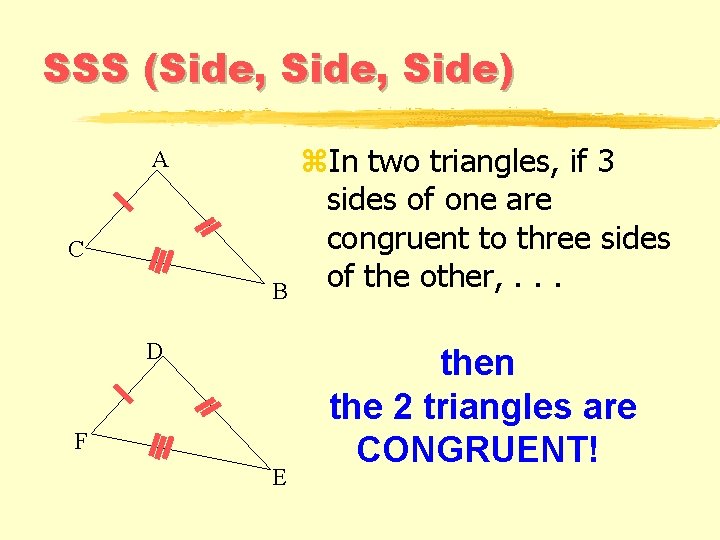
SSS (Side, Side) A C B D F E z. In two triangles, if 3 sides of one are congruent to three sides of the other, . . . then the 2 triangles are CONGRUENT!

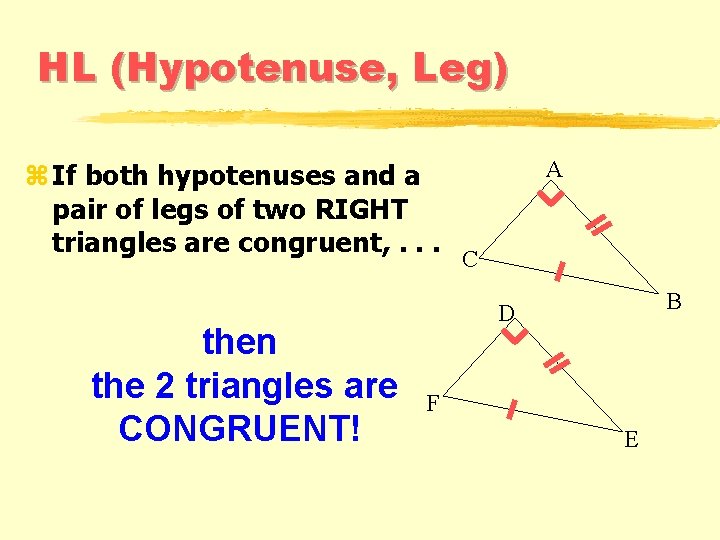
HL (Hypotenuse, Leg) z If both hypotenuses and a pair of legs of two RIGHT triangles are congruent, . . . then the 2 triangles are CONGRUENT! A C B D F E

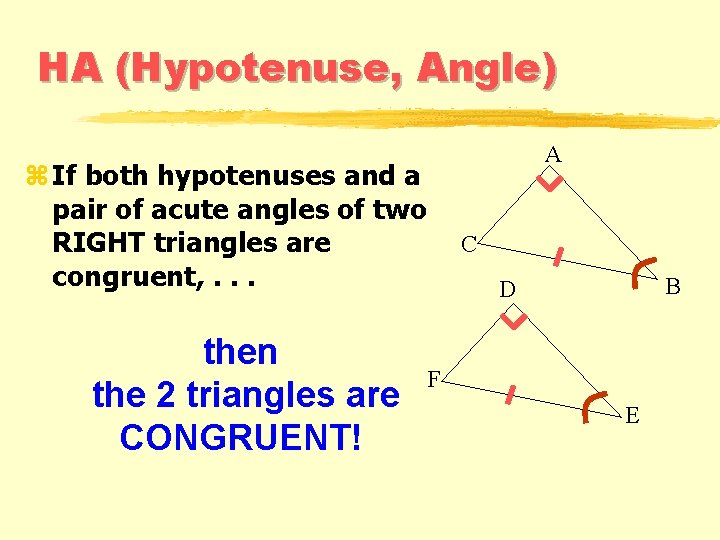
HA (Hypotenuse, Angle) A z If both hypotenuses and a pair of acute angles of two RIGHT triangles are congruent, . . . then the 2 triangles are CONGRUENT! C B D F E

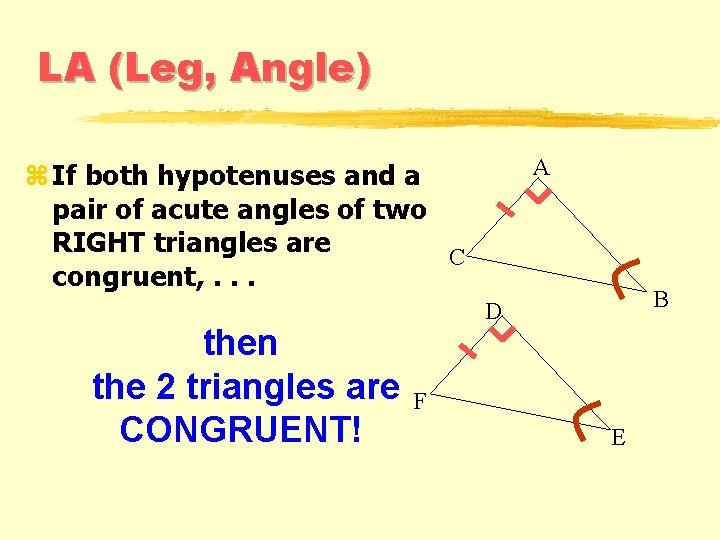
LA (Leg, Angle) A z If both hypotenuses and a pair of acute angles of two RIGHT triangles are C congruent, . . . then the 2 triangles are CONGRUENT! B D F E

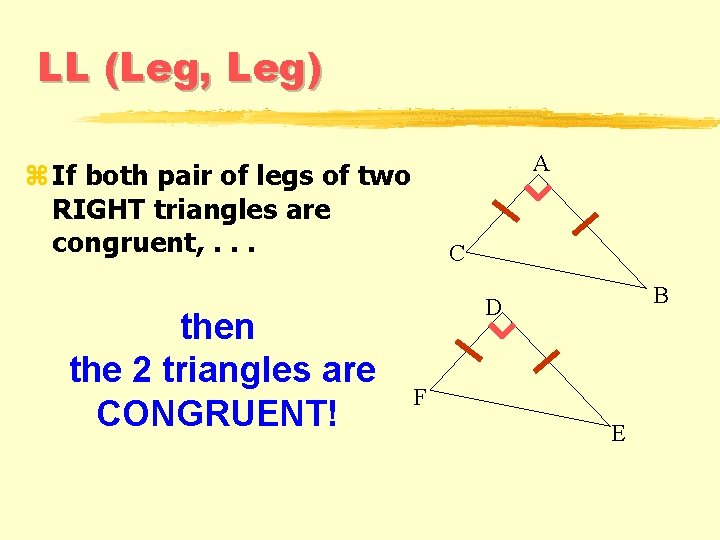
LL (Leg, Leg) A z If both pair of legs of two RIGHT triangles are congruent, . . . then the 2 triangles are CONGRUENT! C B D F E

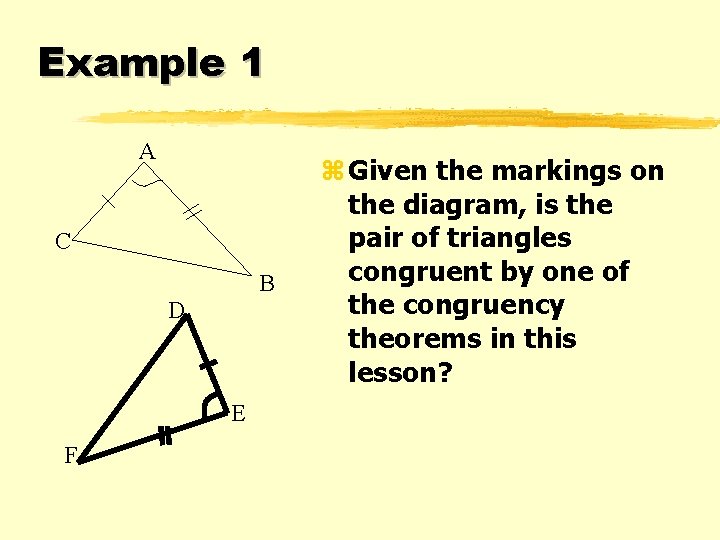
Example 1 A C B D E F z Given the markings on the diagram, is the pair of triangles congruent by one of the congruency theorems in this lesson?

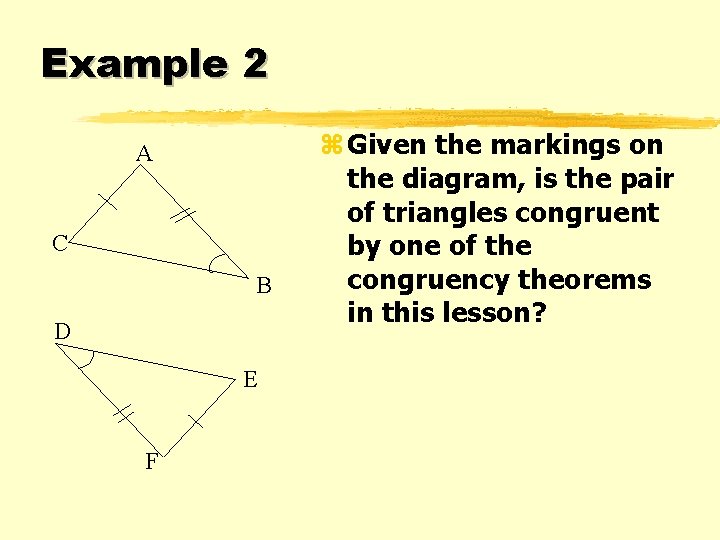
Example 2 A C B D E F z Given the markings on the diagram, is the pair of triangles congruent by one of the congruency theorems in this lesson?

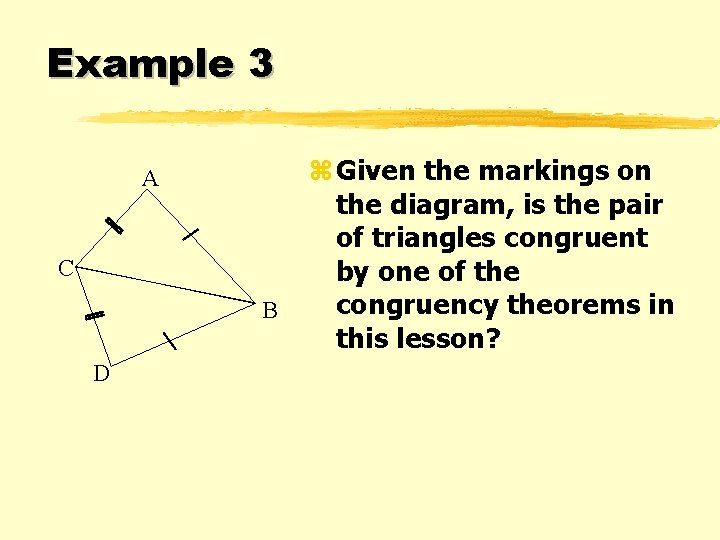
Example 3 A C B D z Given the markings on the diagram, is the pair of triangles congruent by one of the congruency theorems in this lesson?

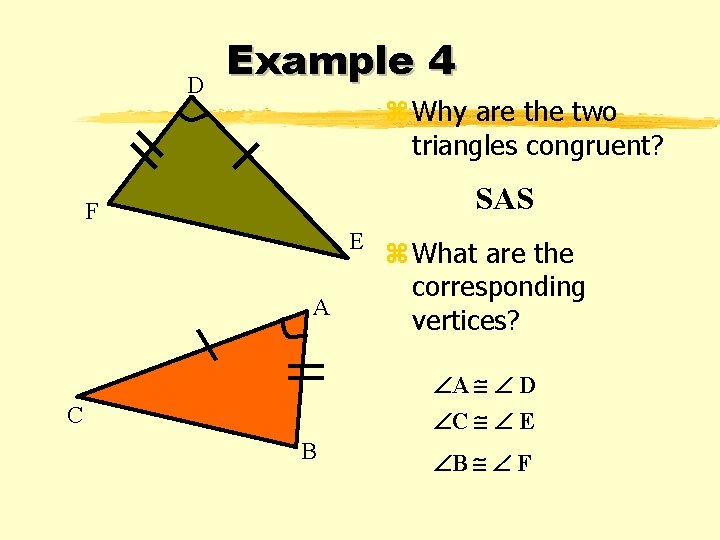
D Example 4 z Why are the two triangles congruent? SAS F E A z What are the corresponding vertices? A D C E C B B F

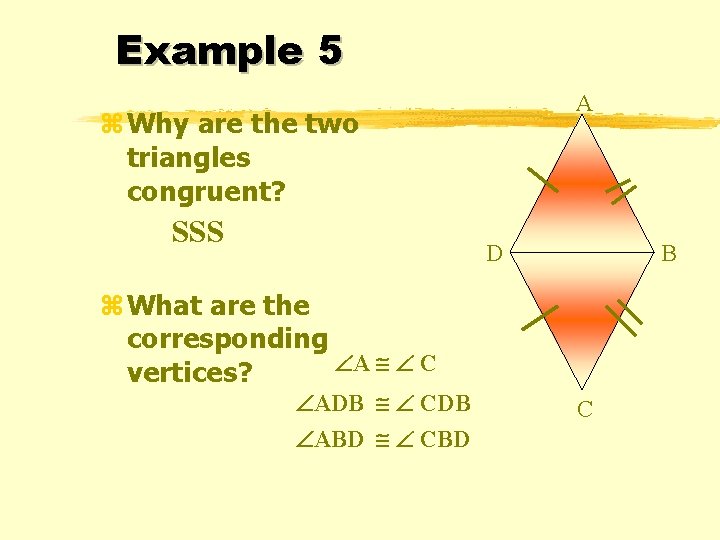
Example 5 A z Why are the two triangles congruent? SSS D B z What are the corresponding A C vertices? ADB CDB ABD C

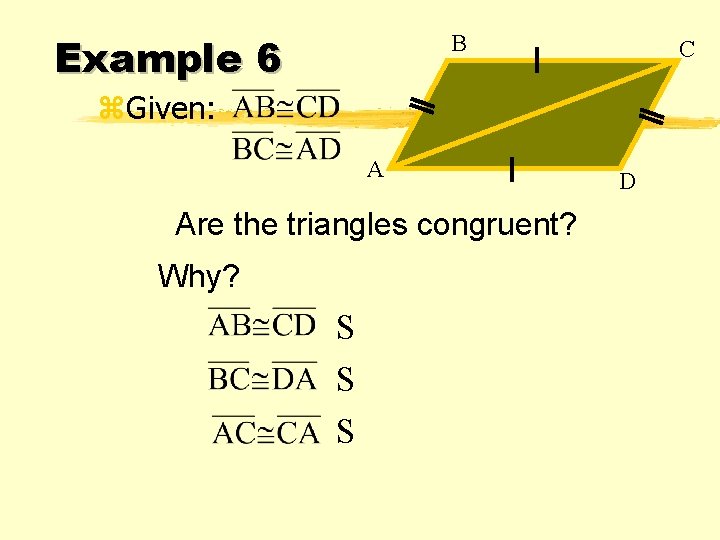
Example 6 B C z. Given: A Are the triangles congruent? Why? S S S D

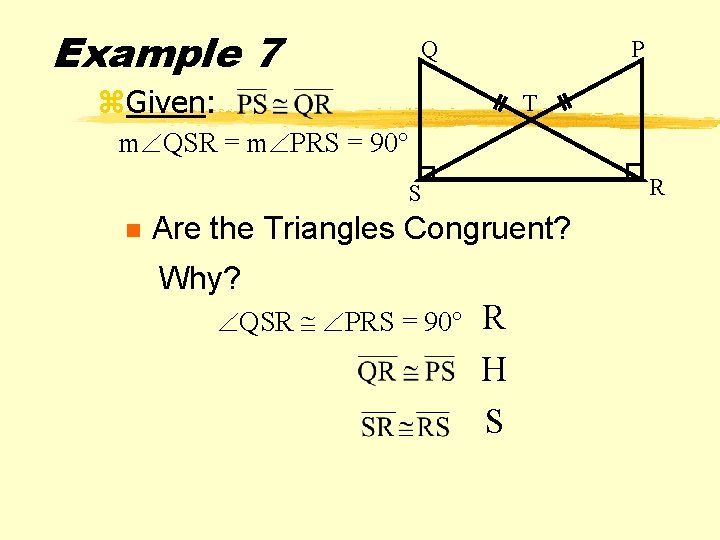
Example 7 Q P z. Given: T m QSR = m PRS = 90° R S n Are the Triangles Congruent? Why? QSR PRS = 90° R H S

Summary: ASA - Pairs of congruent sides contained between two congruent angles AAS – Pairs of congruent angles and the side not contained between them. SAS - Pairs of congruent angles contained between two congruent sides SSS - Three pairs of congruent sides

Summary --for Right Triangles Only: HL – Pair of sides including the Hypotenuse and one Leg HA – Pair of hypotenuses and one acute angle LL – Both pair of legs LA – One pair of legs and one pair of acute angles

THE END!!!