Bi ton 1 V tam gic ABC bit

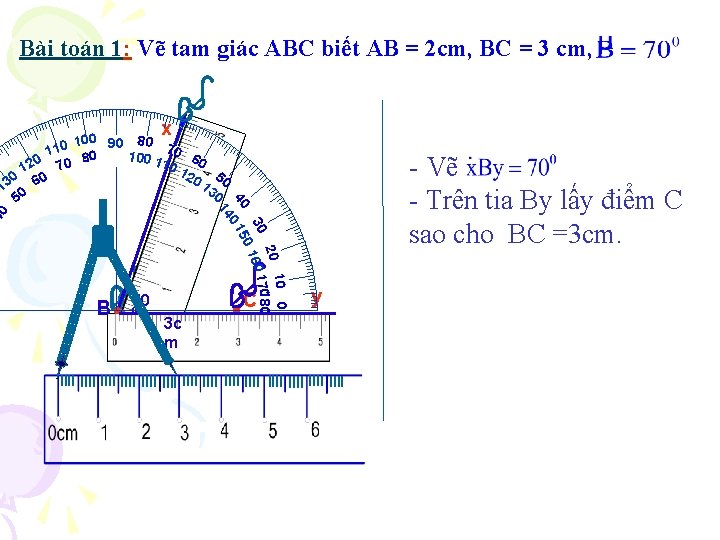
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, x 40 B 70 0 3 c m 10 0 20 180 30 160 170 0 40 0 15 14 100 90 80 77 110 80 100 1 00 60 0 10 70 12 12 0 0 0 1 50 13 0 6 30 5 C - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. y

Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, x A 2 c m B C 70 0 3 c m y - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. - Trên tia Bx lấy điểm A sao cho BA = 2 cm.
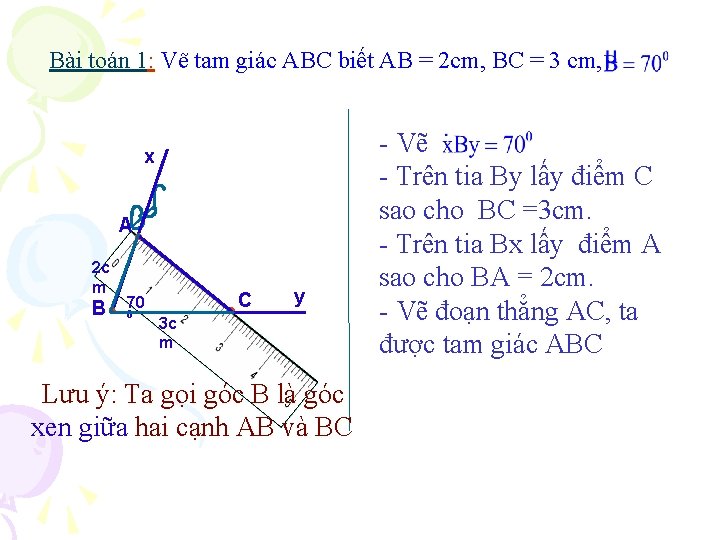
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, x A 2 c m B C 70 0 y 3 c m Lưu ý: Ta gọi góc B là góc xen giữa hai cạnh AB và BC - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. - Trên tia Bx lấy điểm A sao cho BA = 2 cm. - Vẽ đoạn thẳng AC, ta được tam giác ABC
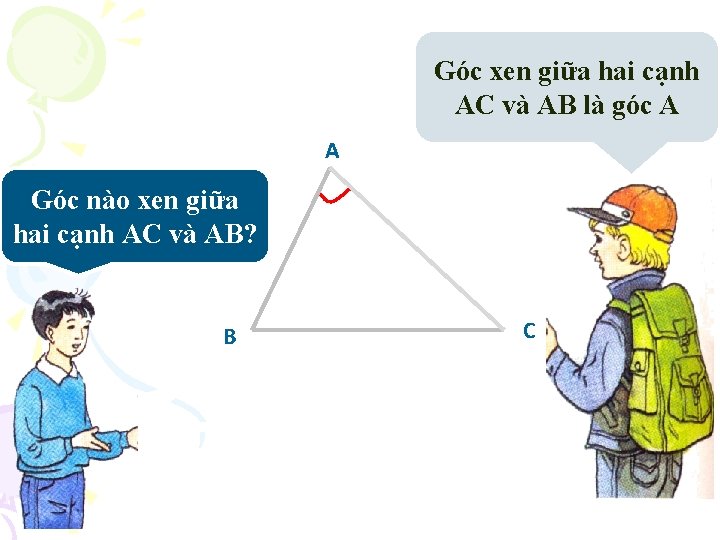
Góc xen giữa hai cạnh AC và AB là góc A A Góc nào xen giữa hai cạnh AC và AB? B C

A Go c C xen giư a hai ca nh CA va CB Góc C xen giữa hai cạnh na o ? B C
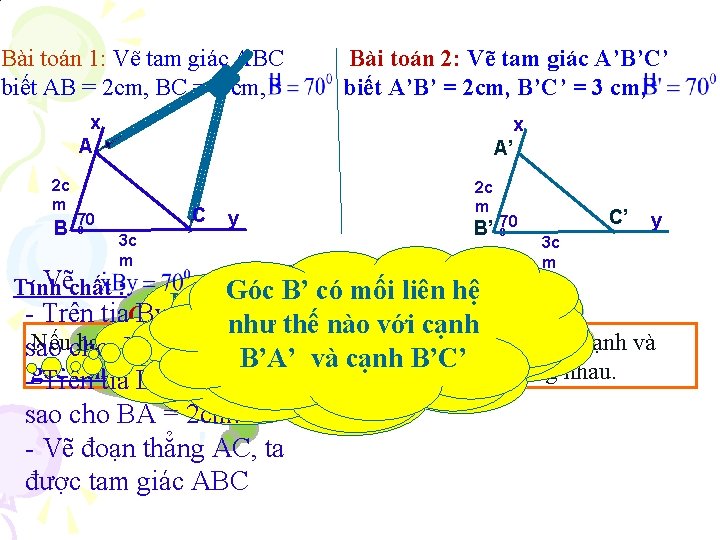
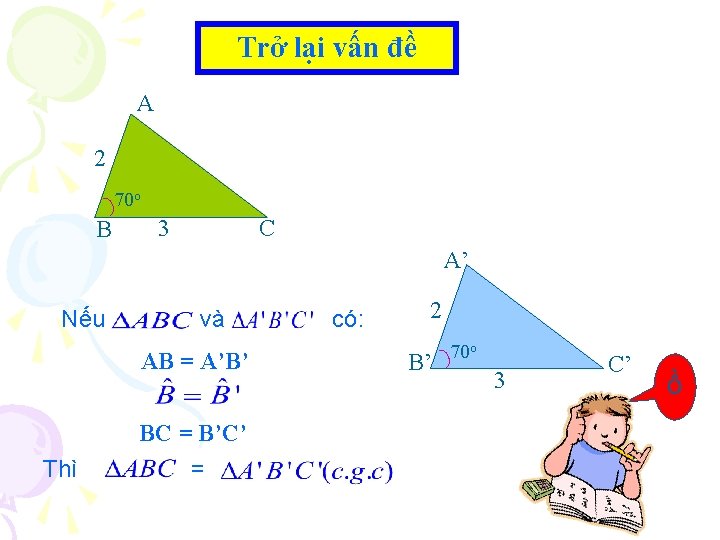
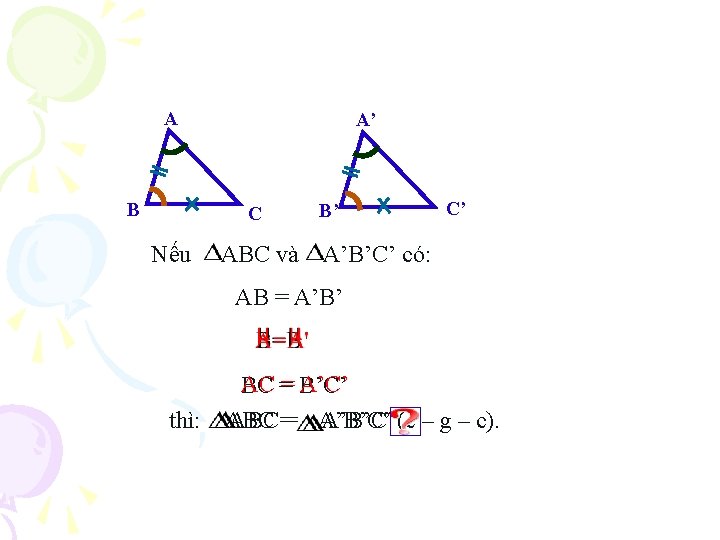
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, Bài toán 2: Vẽ tam giác A’B’C’ biết A’B’ = 2 cm, B’C’ = 3 cm, x A 2 c m B x A’ C 70 0 y 3 c m - Vẽchất : Tính 2 c m B’ C’ 70 0 y 3 c m Góc. BB’ có mối liên hệ Góc có mối liên hệ Ban đầu, tam giác ABC Hãy đo và so nào sánhđểvà AC = A’C’ - Trên tia. Cần By lấy điểm C thêm các điều kiện tam giác như thế nào với cạnh như thế tam giác A’B’C’ có cạnh những ACnào với A’C’ Nếucho hai cạnh xengiác giữa củavới tam giác này bằngtheo hai cạnh và ABC vàgóc tam A’B’C’ bằng nhau sao BC và =3 cm. B’A’ và cạnh B’C’ BA và cạnh BC góc xen giữa của tam giác kia thì hai tam yếu tố nào bằng nhau? các. Acách đã học? giác đó bằng nhau. - Trên tia Bx lấy điểm sao cho BA = 2 cm. - Vẽ đoạn thẳng AC, ta được tam giác ABC
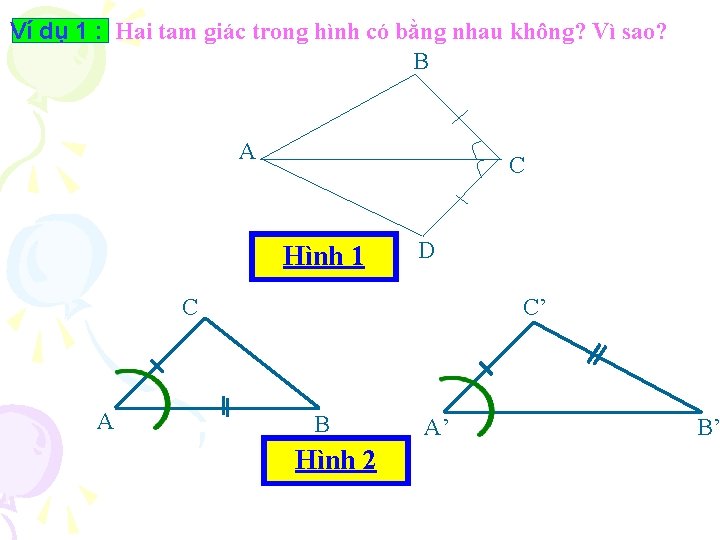
Ví dụ 1 : Hai tam giác trong hình có bằng nhau không? Vì sao? B A C Hình 1 D C A C’ B Hình 2 A’ B’
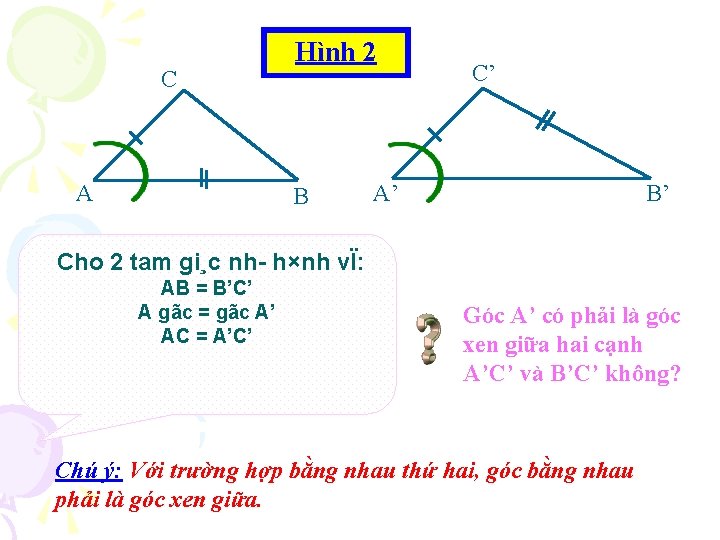
C A Hình 2 B C’ A’ B’ Cho 2 tam gi¸c nh h×nh vÏ: AB = B’C’ A gãc = gãc A’ AC = A’C’ Góc A’ có phải là góc xen giữa hai cạnh A’C’ và B’C’ không? Chú ý: Với trường hợp bằng nhau thứ hai, góc bằng nhau phải là góc xen giữa.
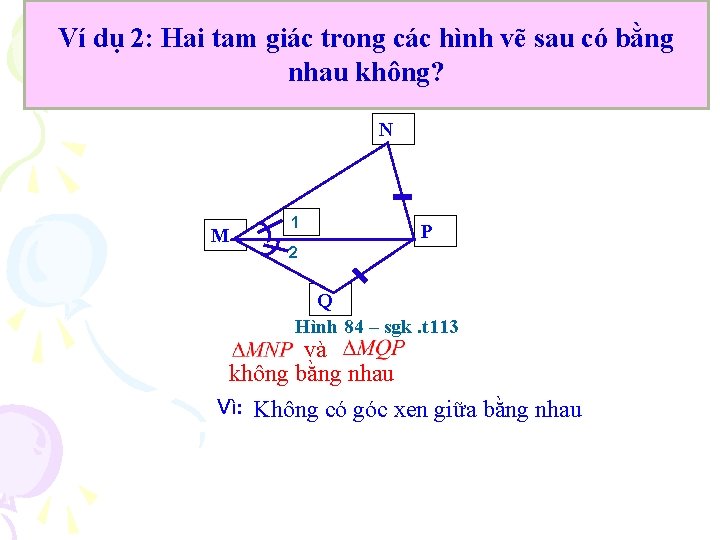
Ví dụ 2: Hai tam giác trong các hình vẽ sau có bằng nhau không? N M 1 P 2 Q Hình 84 – sgk. t 113 và không bằng nhau Vì: Không có góc xen giữa bằng nhau
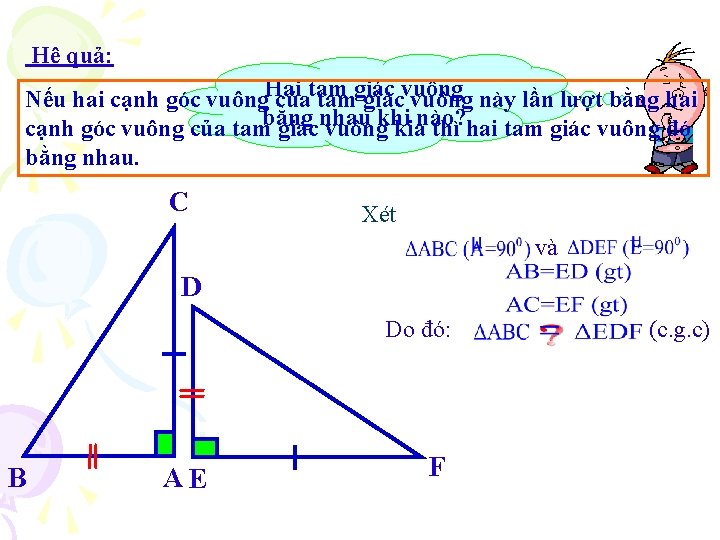
Hệ quả: Nếu hai cạnh góc vuông. Hai củatam tamgiácvuông này lần lượt bằng hai cạnh góc vuông của tambằng giácnhau vuôngkhi kianào? thì hai tam giác vuông đó bằng nhau. C Xét và D Do đó: B AE F (c. g. c)
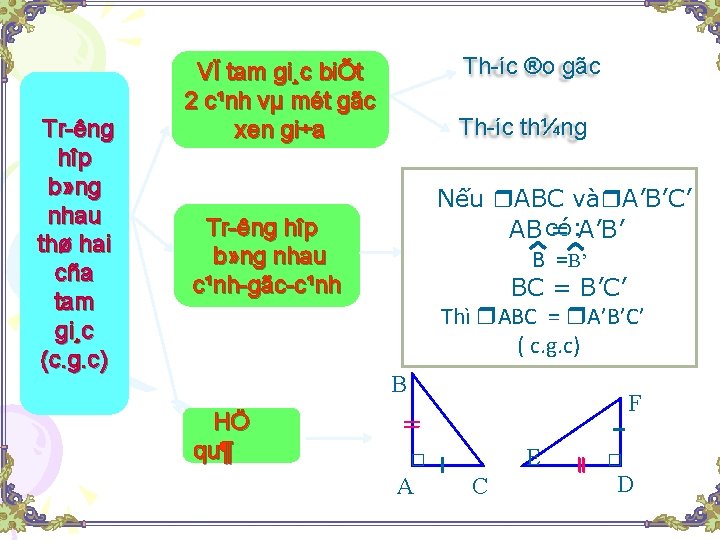
Tr êng hîp b» ng nhau thø hai cña tam gi¸c (c. g. c) Th íc ®o gãc VÏ tam gi¸c biÕt 2 c¹nh vµ mét gãc xen gi÷a Th íc th¼ng Nếu ABC và A’B’C’ AB có: = A’B’ Tr êng hîp b» ng nhau c¹nh gãc c¹nh B =B’ BC = B’C’ Thì ABC = A’B’C’ ( c. g. c) B F HÖ qu¶ E A C D

Bµi tập : Chän c©u tr¶ lêi ®óng: a/ NÕu hai c¹nh vµ một gãc cña tam gi¸c nµy b» ng hai c¹nh vµ một gãc cña tam gi¸c kia th× S hai tam gi¸c ®ã b» ng nhau. b/ NÕu hai c¹nh vµ mét gãc cña tam gi¸c nµy b» ng hai c¹nh vµ mét gãc cña tam gi¸c S kia th× hai tam gi¸c ®ã b» ng nhau. c/ NÕu hai c¹nh vµ gãc xen gi÷a cña tam gi¸c nµy b» ng hai c¹nh vµ gãc xen gi÷a cña § tam gi¸c kia th× hai tam gi¸c ®ã b» ng nhau. d/ C¶ a, b, c ®Òu ®óng. S
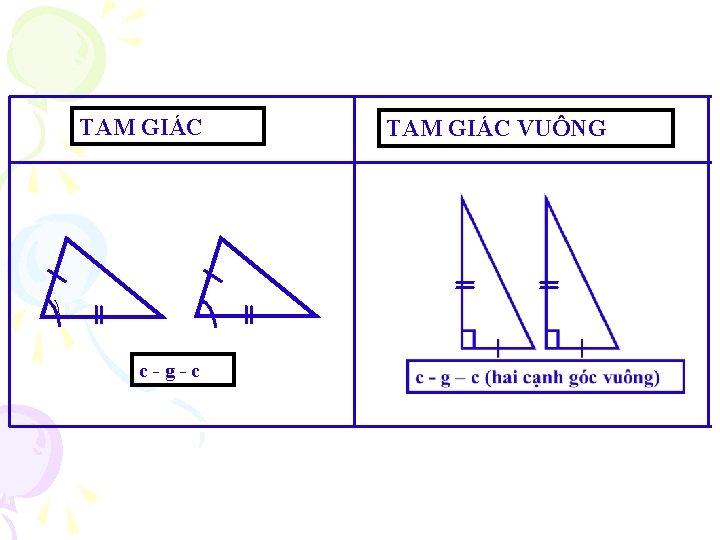
TAM GIÁC c-g-c TAM GIÁC VUÔNG
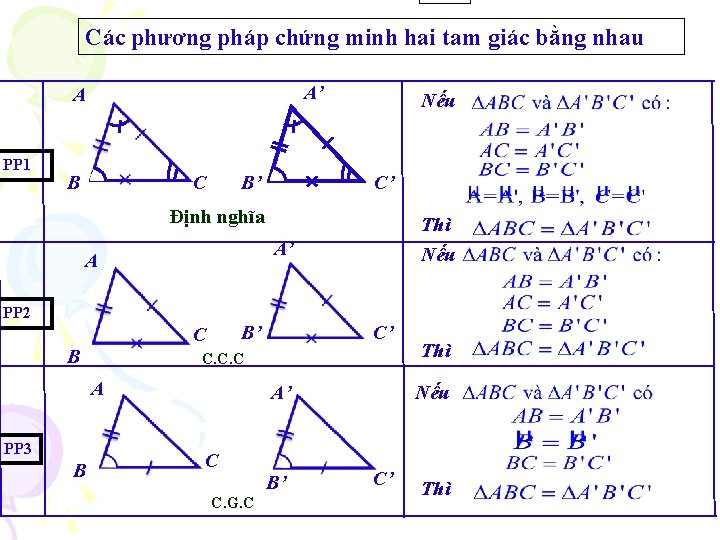
Các phương pháp chứng minh hai tam giác bằng nhau A’ A PP 1 B C B’ Nếu C’ Định nghĩa A’ A PP 2 B’ C B B C’ C. C. C A PP 3 Thì Nếu A’ C B’ C. G. C Thì C’ Thì

øng dông thùc tÕ
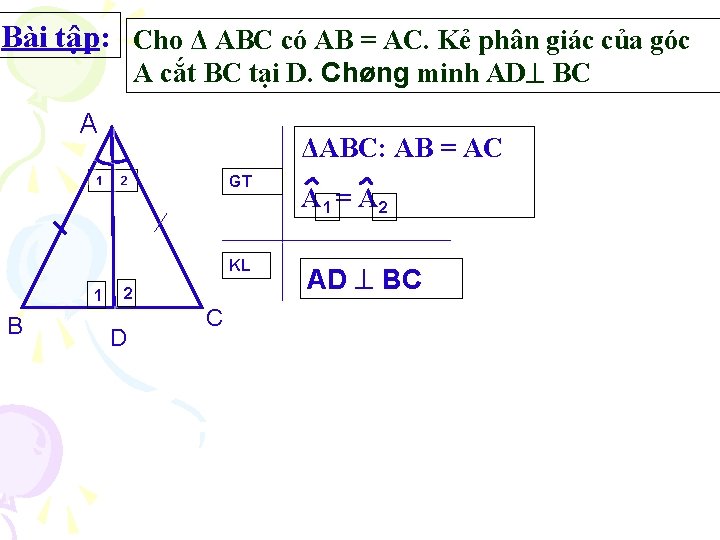
Bài tập: Cho Δ ABC có AB = AC. Kẻ phân giác của góc A cắt BC tại D. Chøng minh AD BC A 1 ΔABC: AB = AC GT 2 KL 1 B 2 D C A 1 = A 2 AD BC

HƯỚNG DẪN VỀ NHÀ - Học thuộc tính chất về trường hợp bằng nhau thứ hai của tam giác và hệ quả trường hợp bằng nhau của hai tam giác vuông. - Làm bài tập 24, 26, 27 sgk/118 -119.

Cám ơn quý thầy cô cùng các em học sinh
- Slides: 21