Bi ging HNH HA V K THUT 1

Bài giảng: HÌNH HỌA & VẼ KỸ THUẬT 1

Bài giảng: HÌNH HỌA&VẼ KỸ THUẬT Biên soạn: Bùi Văn Hảo Năm 2009 BÀI MỞ ĐẦU Hình học họa hình và Vẽ kỹ thuật là các môn kỹ thuật cơ sở được giảng dậy trong các trường đại học ky thuâ t nhằm cung cấp những kiến thức cơ bản về các phương pháp biểu diễn và những kỹ năng cơ bản để thiết lập và đọc các loại bản vẽ kỹ thuật, phục vụ cho nghề nghiệp của các kỹ sư, kỹ thuật viên trong tương lai. Trước mắt để tiềp thu tốt các môn chuyên môn trong quá trình học tập. Môn ho c gô m 2 môn: Hình học Họa hình và Vẽ kỹ thuật. 2

1 -Hình học họa hình: là môn học chuyên nghiên cứu cách biểu diễn không gian hình học(Không gian ơclid) lên trên mặt phẳng nhờ một phép biến đổi đặc biệt gọi là phép chiếu. Hiện có hai phép chiếu là phép chiếu song và phép chiếu xuyên tâm(hay phối cảnh). Người ta còn mở rộng hai phép chiếu này thành những phép chiếu ứng dụng khác như phép chiếu trục đo, có số… 3

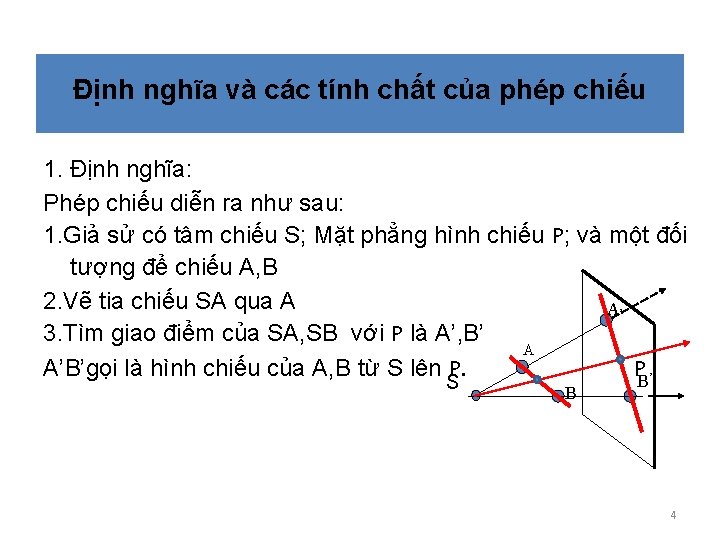
Định nghĩa và các tính chất của phép chiếu 1. Định nghĩa: Phép chiếu diễn ra như sau: 1. Giả sử có tâm chiếu S; Mặt phẳng hình chiếu P; và một đối tượng để chiếu A, B 2. Vẽ tia chiếu SA qua A A, 3. Tìm giao điểm của SA, SB với P là A’, B’ A A’B’gọi là hình chiếu của A, B từ S lên P. PB’ S B 4

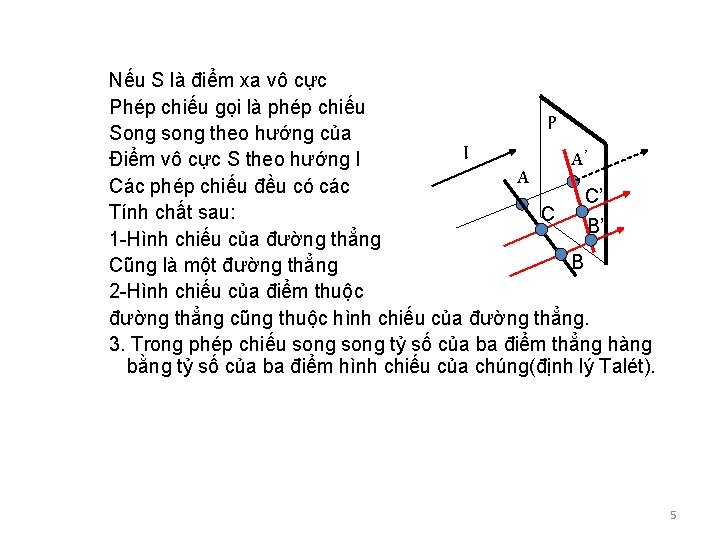
Nếu S là điểm xa vô cực Phép chiếu gọi là phép chiếu P Song song theo hướng của A’ Điểm vô cực S theo hướng l A Các phép chiếu đều có các C’ Tính chất sau: C B’ 1 -Hình chiếu của đường thẳng B Cũng là một đường thẳng 2 -Hình chiếu của điểm thuộc đường thẳng cũng thuộc hình chiếu của đường thẳng. 3. Trong phép chiếu song tỷ số của ba điểm thẳng hàng bằng tỷ số của ba điểm hình chiếu của chúng(định lý Talét). l 5

2. Tính chất của phép chiếu • 1. Bảo tồn tính chất đường thẳng chiếu thành đường thẳng. • 2. Bảo tồn tính liên thuộc giữa điểm và đường thẳng với các yếu tố khác của không gian. • 3. Bảo tồn tỷ số kép của 4 điểm thẳng hàng(trong phép chiếu xuyên tâm) và tỷ số đơn của 3 điểm thẳng hàng(trong phép chiếu song)và các hệ quả của chúng. • 4. Ba o tô n ti nh song cu a hai đươ ng thă ng. 6

Chương 1 PHƯƠNG PHÁP HAI HÌNH CHIẾU THẲNG GÓC (phương pháp của Gaspa Monge 1746 -1818) 2. 1 Biểu diễn các yếu tố hình học cơ bản: Điểm; Đường thẳng; Mặt phẳng 2. 1. 1 Biểu diễn điểm, cách xây dựng hình biểu diễn của điểm bằng phương pháp hai hình chiếu thẳng góc(gọi tắt là Đồ thức) Giả sử chúng ta cần chiếu một điểm A ta làm như sau: 1. Chọn trước hai mặt phẳng P 1 và P 2 và đặt vuông góc nhau lần lượt đặt thẳng đứng và nằm ngang với P 1 gọi là mặt phẳng hình chiếu đứng; P 2 là mặt phẳng hình chiếu bằng. 7

• 2. Lần lượt chiếu điểm A thẳng góc lên P 1 và P 2 có các hình chiếu trên P 1 là A 1 và trên P 2 là A 2. Đặt tên lần lượt là hình chiếu đứng và hình chiếu bằng của điểm A. • 3. Chập P 2 vào P 1 quanh giao tuyến xx (gọi là trục hình chiếu)của P 1 và P 2; Có cặp điểm A 1, A 2 với A 1 A 2 vuông góc với xx (gọi là đường gióng). A 1, A 2 gọi là hình biểu diễn bằng phương pháp hai hình chiếu thẳng góc của A(gọi tắt là đồ thức của điểm A). 8

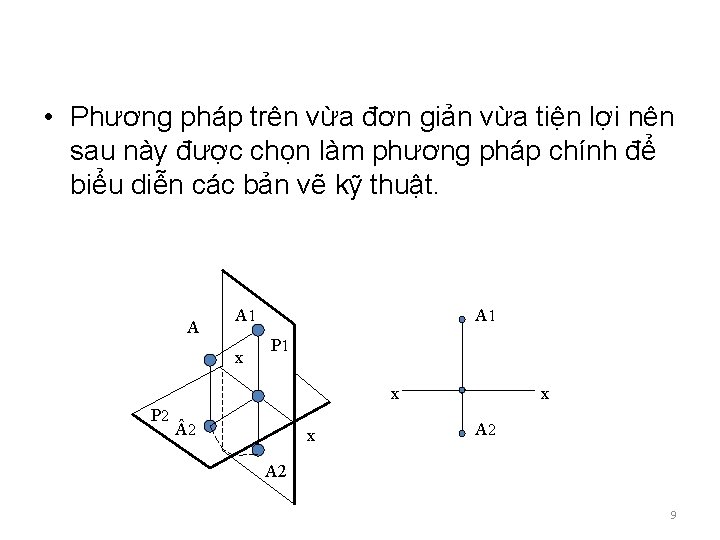
• Phương pháp trên vừa đơn giản vừa tiện lợi nên sau này được chọn làm phương pháp chính để biểu diễn các bản vẽ kỹ thuật. A A 1 x A 1 P 1 x P 2 2 x x A 2 9

2. 1. 2 Biểu diễn đường thẳng • Đường thẳng được xác định bởi hai điểm. Vậy hình biểu diễn của đường thẳng là các hình biểu diễn của hai điểm của đường thẳng đó. (Từ nay về sau ta gọi hình biểu diễn của các yếu tố của không gian là đồ thức) 10

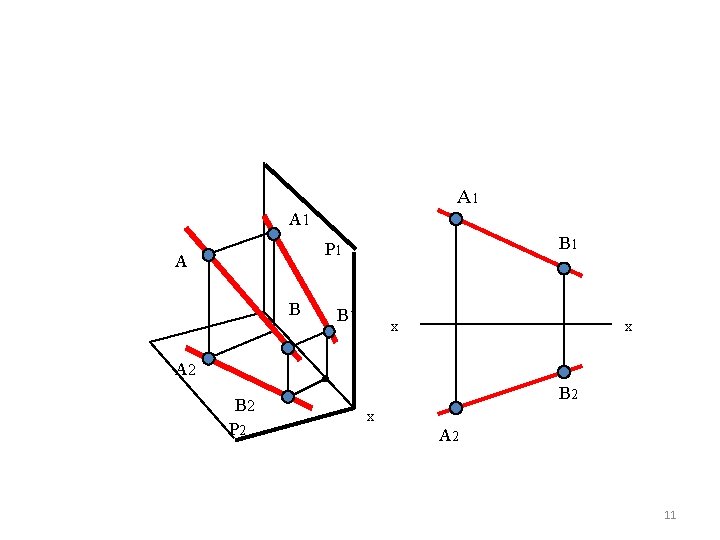
A 1 B 1 P 1 A B B 1 x x A 2 B 2 P 2 B 2 x A 2 11

• Đường thẳng nói trên gọi là đường thẳng có vị trí bất kỳ đối với các mặt phẳng hình chiếu. Ngoài ra đường thẳng trong không gian còn có các đ/th có vị trí vuông góc(gọi là các đ/th chiếuvà các đ/th //với các mặt phẳng hình chiếu gọi là các đ/th đồng mức: //P 1 gọi là đường mặt; // P 2 gọi là đường bằng; // P 3 gọi là đường cạnh. Các tính chất của các đường thẳng này các bạn tự suy ra. Chúng có rất nhiều ứng dụng sau này trong việc giải các bài toán HH cũng như biểu diễn vật thể. 12

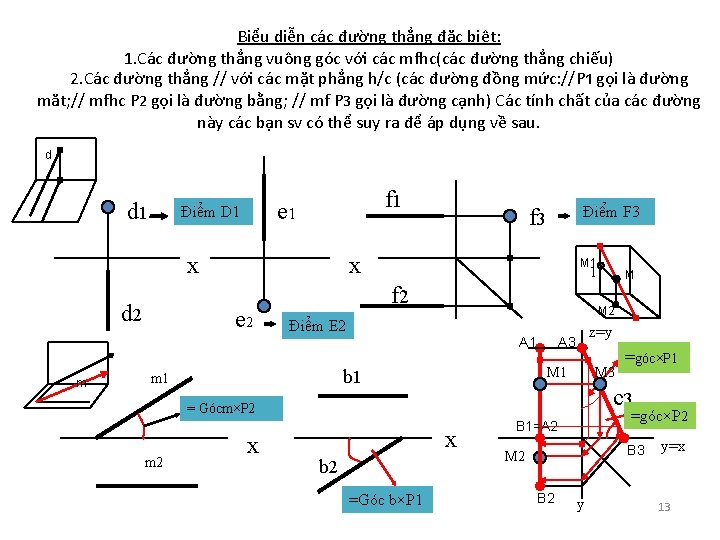
Biểu diễn các đường thẳng đặc biệt: 1. Các đường thẳng vuông góc với các mfhc(các đường thẳng chiếu) 2. Các đường thẳng // với các mặt phẳng h/c (các đường đồng mức: //P 1 gọi là đường măt; // mfhc P 2 gọi là đường bằng; // mf P 3 gọi là đường cạnh) Các tính chất của các đường này các bạn sv có thể suy ra để áp dụng về sau. d d 1 f 1 e 1 Điểm D 1 x d 2 Điê m F 3 f 3 x e 2 M 1 1 f 2 M 2 Điểm E 2 A 1 m z=y A 3 M 1 b 1 m 1 M 3 m 2 x b 2 =Góc b×P 1 =góc×P 1 c 3 = Gócm×P 2 x M =góc×P 2 B 1=A 2 B 3 M 2 B 2 y y=x 13

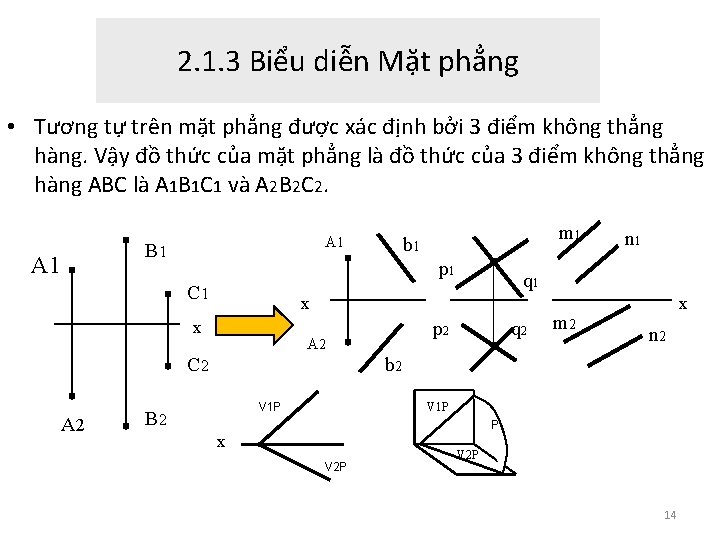
2. 1. 3 Biểu diễn Mặt phẳng • Tương tự trên mặt phẳng được xác định bởi 3 điểm không thẳng hàng. Vậy đồ thức của mặt phẳng là đồ thức của 3 điểm không thẳng hàng ABC là A 1 B 1 C 1 và A 2 B 2 C 2. A 1 B 1 A 1 p 1 C 1 p 2 A 2 C 2 n 1 q 1 x x A 2 m 1 b 1 q 2 m 2 x n 2 b 2 V 1 P B 2 V 1 P P x V 2 P 14

Các mặt phẳng được biểu diễn như trên gọi là các mặt phẳng có vị trí bất kỳ. Ngoài ra mặt phẳng còn có các vị trí vuông góc hay song với các mặt phẳng hình chiếu gọi là các mặt phẳng đặc biệt: chúng có rất nhiều ứng dụng trong việc biểu diễn vật thể trong vẽ kỹ thuật; cũng như giải các bài toán hình hoạ ở các phần tiếp sau. • 1. Vuông góc với mặt phẳng hình chiếu đứng gọi là mặt phẳng chiếu đứng; vuông góc với mặt phẳng hình chiếu bằng gọi là mặt phẳng chiếu bằng; với mặt phẳng hình chiếu cạnh gọi là mặt phẳng chiếu cạnh (haycòn gọi là mặt phẳng song với trục xx). • 2. Song song với mặt phẳng hình(hay co n go i la mă t phă ng đô ng mư c); Nê u // vơ i mă t phă ng hi nh chiếu đứng gọi là mặt phẳng mặt; //vơ i mă t phă ng hi nh chiê u bă ng go i la mă t phă ng bă ng. 15

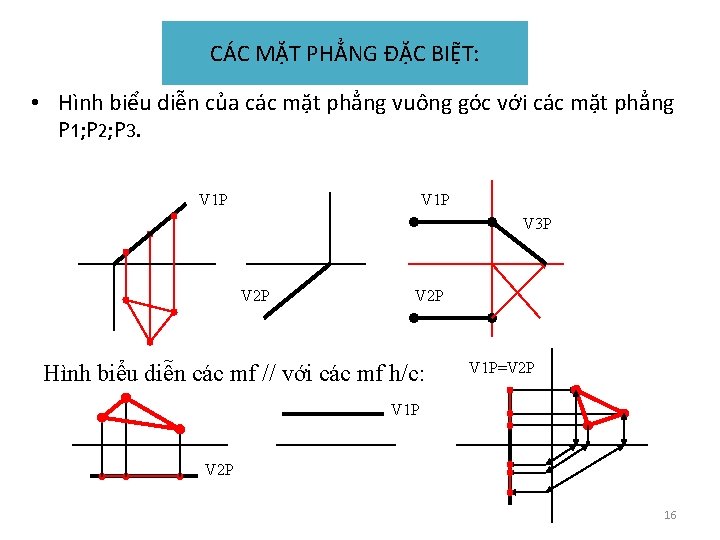
CÁC MẶT PHẲNG ĐẶC BIỆT: • Hình biểu diễn của các mặt phẳng vuông góc với các mặt phẳng P 1; P 2; P 3. V 1 P V 3 P V 2 P Hình biểu diễn các mf // với các mf h/c: V 1 P=V 2 P V 1 P V 2 P 16

2. 2 Đường thẳng, điểm thuộc mặt phẳng. • Hai mệnh đề hi nh ho c sau dễ dàng a p du ng cho các phép chiếu. • 1/ Đường thẳng thuộc mặt phẳng thì phải có hai điểm thuộc mặt phẳng. • 2/ Điểm thuộc mặt phẳng thì nó phải thuộc một đường thẳng của mặt phẳng. • Vì vậy hình chiếu của chúng cũng phải thỏa mãn các tính chất đó. 17

Hai định lý cơ bản trên được phát biểu thành hai bài toán chỉ dẫn cách thực hiện trên đồ thức như sau: • Bài toán 1: Cho đường thẳng AB thuộc mặt phẳng P(được xác định bằng một trong cách trên) mà đã có một hình chiếu của nó tìm hình chiếu thư hai của nó. • Bài toán 2: Cho điểm A thuộc mặt phẳng P mà một hình chiếu của A đã biết. Xác định nốt hình chiếu còn lại. 18

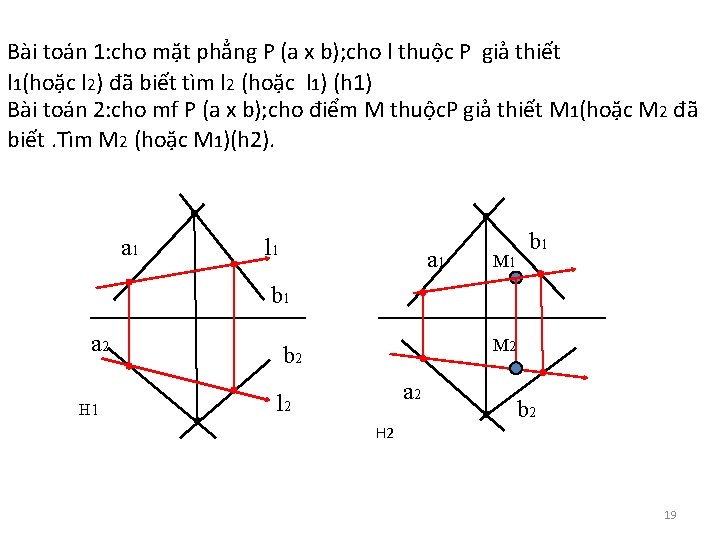
Bài toán 1: cho mặt phẳng P (a x b); cho l thuộc P giả thiết l 1(hoặc l 2) đã biết tìm l 2 (hoặc l 1) (h 1) Bài toán 2: cho mf P (a x b); cho điểm M thuộc. P giả thiết M 1(hoặc M 2 đã biết. Tìm M 2 (hoặc M 1)(h 2). a 1 l 1 a 1 M 1 b 1 a 2 H 1 M 2 b 2 a 2 l 2 b 2 H 2 19

2. 3 Tương quan vị trí giữa các yếu tố Hình học. • Ngoài mối tương quan liên thuộc như đã trình bày các yếu tố hình học ở ngoài nhau chúng còn có các tương quan khác như cắt nhau, song nhau, chéo nhau…Ta xét các tương quan này thể hiện trên đồ thức như thế nào? v 1/ Hai đường thẳng cắt nhau; song, chéo nhau v 2/ Hai mặt phẳng cắt nhau. v 3/ Đường thẳng cắt mặt phẳng. Kể cả trường hợp cắt vuông góc với mặt phẳng. 20

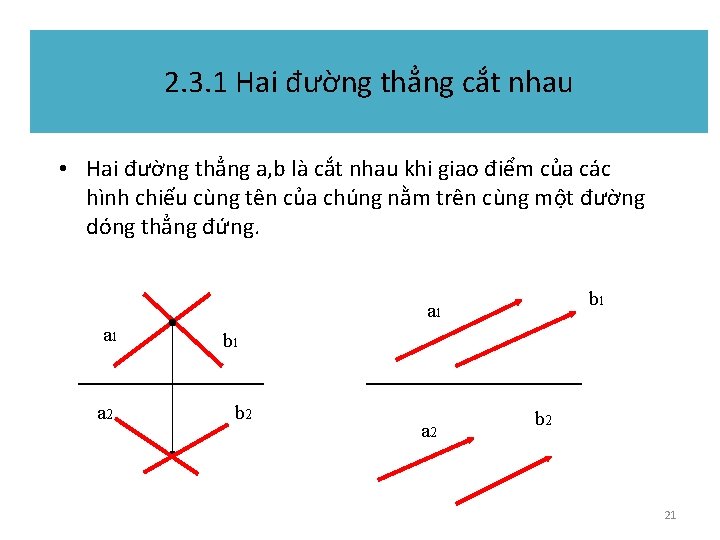
2. 3. 1 Hai đường thẳng cắt nhau • Hai đường thẳng a, b là cắt nhau khi giao điểm của các hình chiếu cùng tên của chúng nằm trên cùng một đường dóng thẳng đứng. b 1 a 1 a 2 b 1 b 2 a 2 b 2 21

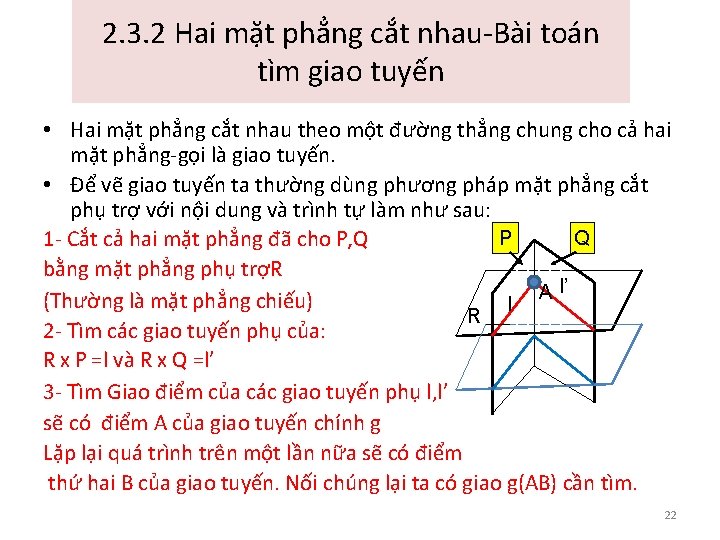
2. 3. 2 Hai mặt phẳng cắt nhau-Bài toán tìm giao tuyến • Hai mặt phẳng cắt nhau theo một đường thẳng chung cho cả hai mặt phẳng-gọi là giao tuyến. • Để vẽ giao tuyến ta thường dùng phương pháp mặt phẳng cắt phụ trợ với nội dung và trình tự làm như sau: P Q 1 - Cắt cả hai mặt phẳng đã cho P, Q bằng mặt phẳng phụ trợR l’ A (Thường là mặt phẳng chiếu) l R 2 - Tìm các giao tuyến phụ của: R x P =l và R x Q =l’ 3 - Tìm Giao điểm của các giao tuyến phụ l, l’ sẽ có điểm A của giao tuyến chính g Lặp lại quá trình trên một lần nữa sẽ có điểm thứ hai B của giao tuyến. Nối chúng lại ta có giao g(AB) cần tìm. 22

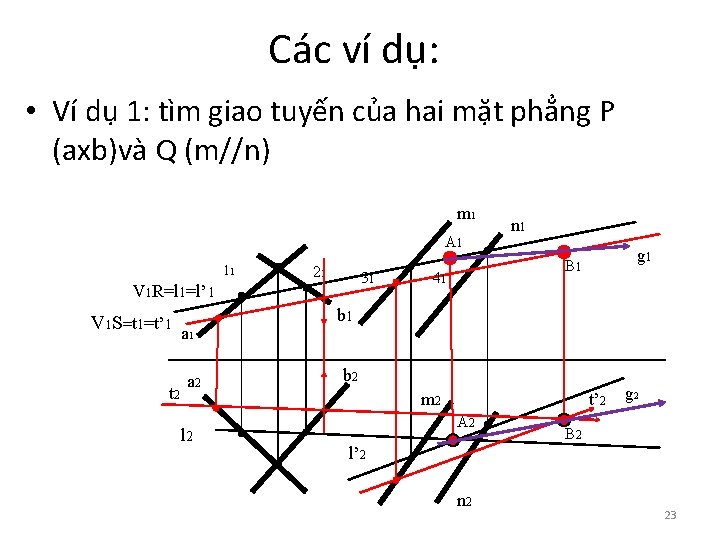
Các ví dụ: • Ví dụ 1: tìm giao tuyến của hai mặt phẳng P (axb)và Q (m//n) m 1 A 1 11 21 31 V 1 R=l 1=l’ 1 V 1 S=t 1=t’ 1 t 2 a 1 a 2 l 2 n 1 g 1 B 1 41 b 2 m 2 t’ 2 A 2 g 2 B 2 l’ 2 n 2 23

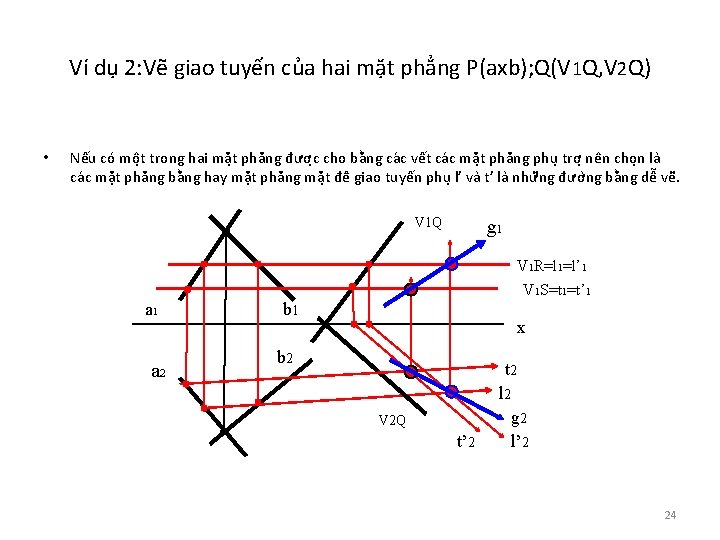
Ví dụ 2: Vẽ giao tuyến của hai mặt phẳng P(axb); Q(V 1 Q, V 2 Q) • Nếu co mô t trong hai mă t phă ng đươ c cho bằng ca c vết ca c mă t phă ng phu trơ nên cho n la ca c mă t phă ng bằng hay mă t phă ng mă t đê giao tuyến phu l’ va t’ la như ng đươ ng bằng dễ ve. V 1 Q g 1 V 1 R=l 1=l’ 1 V 1 S=t 1=t’ 1 a 2 b 1 x b 2 t 2 V 2 Q t’ 2 l 2 g 2 l’ 2 24

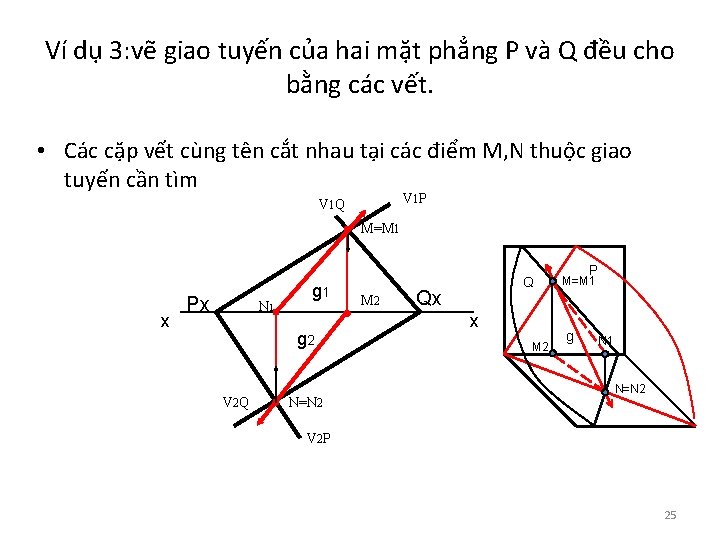
Ví dụ 3: vẽ giao tuyến của hai mặt phẳng P và Q đều cho bằng các vết. • Các cặp vết cùng tên cắt nhau tại các điểm M, N thuộc giao tuyến cần tìm V 1 P V 1 Q M=M 1 x Px N 1 g 2 V 2 Q N=N 2 M 2 Q Qx x M 2 P M=M 1 g N 1 N=N 2 V 2 P 25

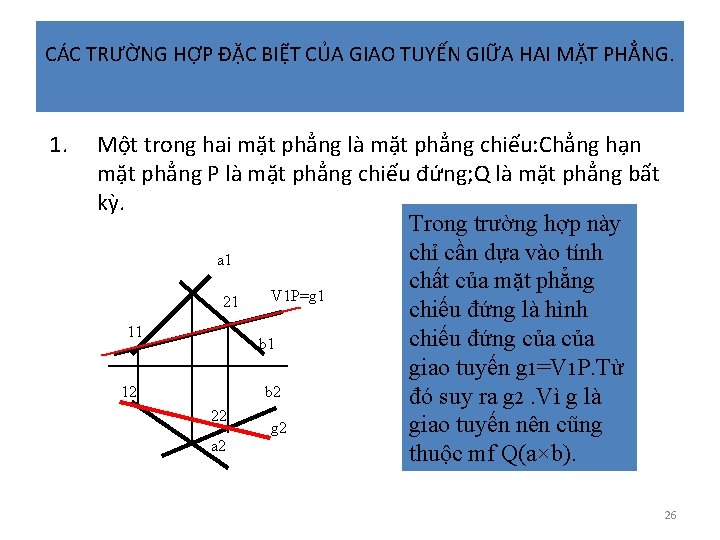
CÁC TRƯỜNG HỢP ĐẶC BIỆT CỦA GIAO TUYẾN GIỮA HAI MẶT PHẲNG. 1. Một trong hai mặt phẳng là mặt phẳng chiếu: Chẳng hạn mặt phẳng P là mặt phẳng chiếu đứng; Q là mặt phẳng bất kỳ. Trong trường hợp này chỉ cần dựa vào tính a 1 chất của mặt phẳng V 1 P=g 1 21 chiếu đứng là hình 11 chiếu đứng của b 1 giao tuyến g 1=V 1 P. Từ 12 b 2 đó suy ra g 2. Vì g là 22 giao tuyến nên cũng g 2 a 2 thuộc mf Q(a×b). 26

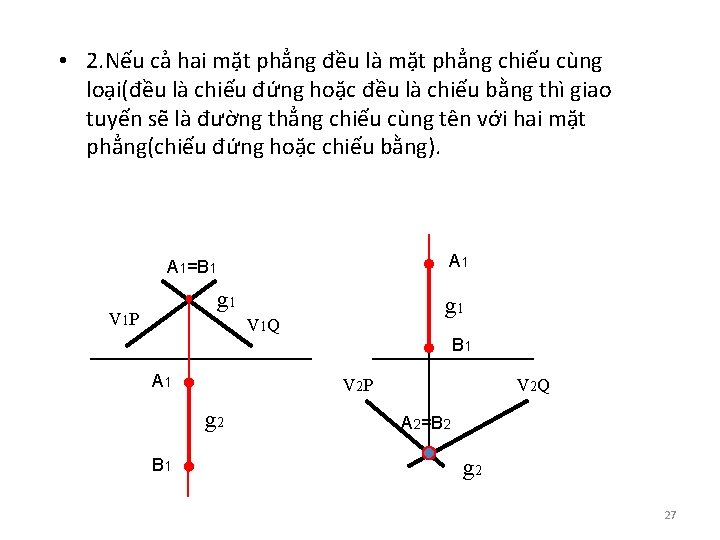
• 2. Nếu cả hai mặt phẳng đều là mặt phẳng chiếu cùng loại(đều là chiếu đứng hoặc đều là chiếu bằng thì giao tuyến sẽ là đường thẳng chiếu cùng tên với hai mặt phẳng(chiếu đứng hoặc chiếu bằng). A 1=B 1 g 1 V 1 P g 1 V 1 Q A 1 V 2 P g 2 B 1 V 2 Q A 2=B 2 g 2 27

3. Nếu hai mặt phẳng P và Q là các mặt phẳng chiếu khác loại nhau. (chẳng hạn P là mf chiếu đứng còn Q là chiếu bằng hoặc ngược lại) lúc đó các hình chiếu của giao tuyến sẽ trùng với hình chiếu cùng tên của mặt phẳng V 1 P=g 1 V 2 Q=g 2 28

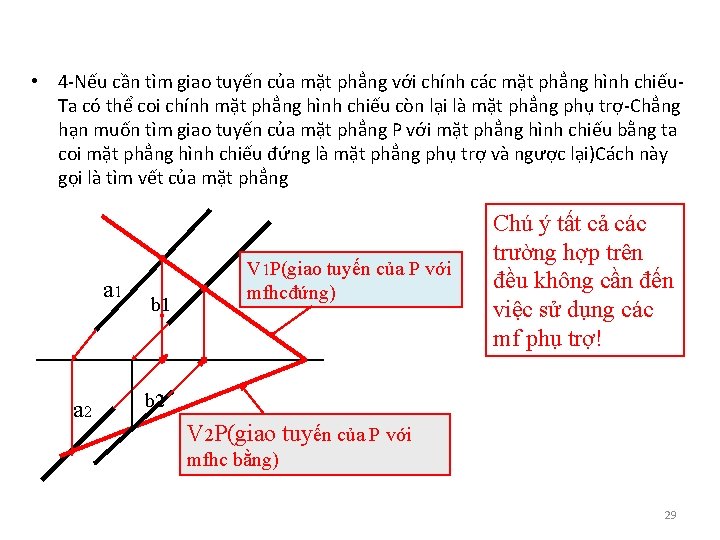
• 4 -Nếu cần tìm giao tuyến của mặt phẳng với chính các mặt phẳng hình chiếu. Ta có thể coi chính mặt phẳng hình chiếu còn lại là mặt phẳng phụ trợ-Chẳng hạn muốn tìm giao tuyến của mặt phẳng P với mặt phẳng hình chiếu bằng ta coi mặt phẳng hình chiếu đứng là mặt phẳng phụ trợ và ngược lại)Cách này gọi là tìm vết của mặt phẳng a 1 a 2 b 1 V 1 P(giao tuyến của P với mfhcđứng) Chú ý tất cả các trường hợp trên đều không cần đến việc sử dụng các mf phụ trợ! b 2 V 2 P(giao tuyến của P với mfhc bằng) 29

2. 3. 3 ĐƯỜNG THẲNG VÀ MẶT PHẲNG • 2. 3. 4 Vị trí của đường thẳng và mặt phẳng-Bài toán giao điểm của đường thẳng và mặt phẳng. • Đường thẳng và mặt phẳng trong không gian có thể trùng nhau (đã xét đến ở trên); Có thể cắt nhau hoặc song nhau. Nếu cắt nhau thì chúng có 1điểm chung thực. Nếu song nhau thì điểm chung là ảo(không thực mà ở xa vô cực) 30

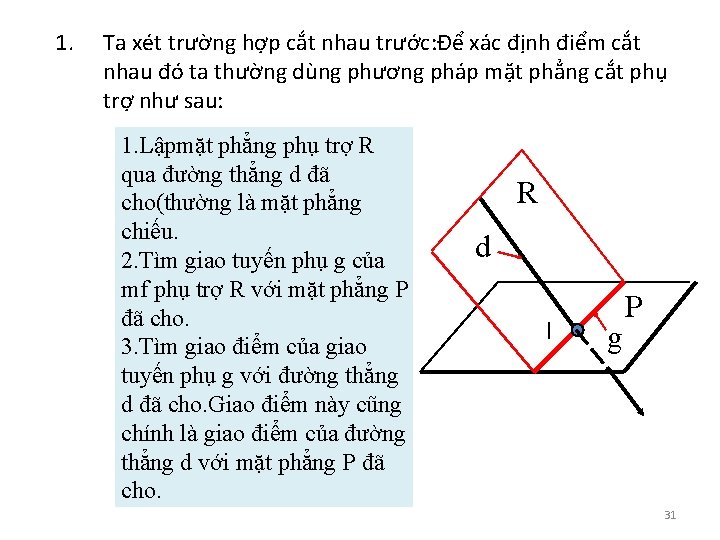
1. Ta xét trường hợp cắt nhau trước: Để xác định điểm cắt nhau đó ta thường dùng phương pháp mặt phẳng cắt phụ trợ như sau: 1. Lậpmặt phẳng phụ trợ R qua đường thẳng d đã cho(thường là mặt phẳng chiếu. 2. Tìm giao tuyến phụ g của mf phụ trợ R với mặt phẳng P đã cho. 3. Tìm giao điểm của giao tuyến phụ g với đường thẳng d đã cho. Giao điểm này cũng chính là giao điểm của đường thẳng d với mặt phẳng P đã cho. R d I g P 31

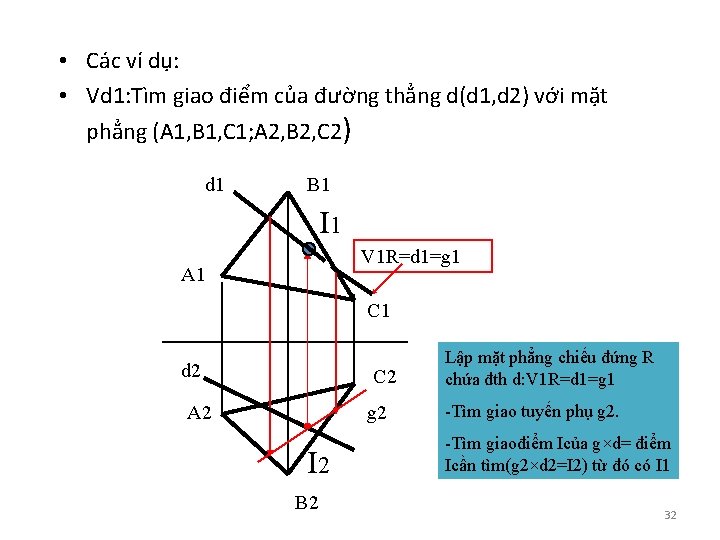
• Các ví dụ: • Vd 1: Tìm giao điểm của đường thẳng d(d 1, d 2) với mặt phẳng (A 1, B 1, C 1; A 2, B 2, C 2) d 1 B 1 I 1 V 1 R=d 1=g 1 A 1 C 1 d 2 C 2 A 2 g 2 I 2 B 2 Lập mặt phẳng chiếu đứng R chứa đth d: V 1 R=d 1=g 1 -Tìm giao tuyến phụ g 2. -Tìm giaođiểm Icủa g×d= điểm Icần tìm(g 2×d 2=I 2) từ đó có I 1 32

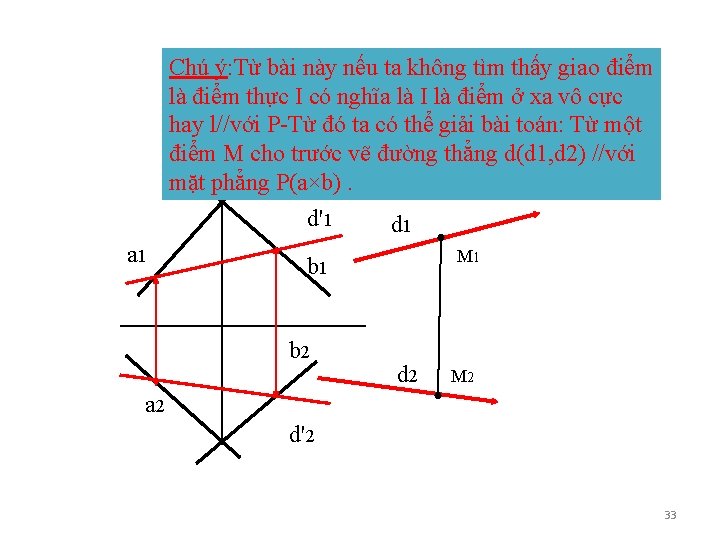
Chú ý: Từ bài này nếu ta không tìm thấy giao điểm là điểm thực I có nghĩa là I là điểm ở xa vô cực hay l//với P-Từ đó ta có thể giải bài toán: Từ một điểm M cho trước vẽ đường thẳng d(d 1, d 2) //với mặt phẳng P(a×b). d'1 a 1 d 1 M 1 b 2 d 2 M 2 a 2 d'2 33

• Nếu đường thẳng d //với mf P hay có thể nói d cắt P tại điểm vô tận. Trước đây ta đã có mệnh đề hình học quen thuộc: Đường thẳng d muốn // với mặt phẳng P thì d phải // với một đường thẳng d' thuộc mặt phẳng P. Dựa vào mệnh đề này dễ dàng biểu diễn được đường thẳng // với mặt phẳng trong phương pháp hai hình chiếu thẳng góc. (hình vẽ trên). 34

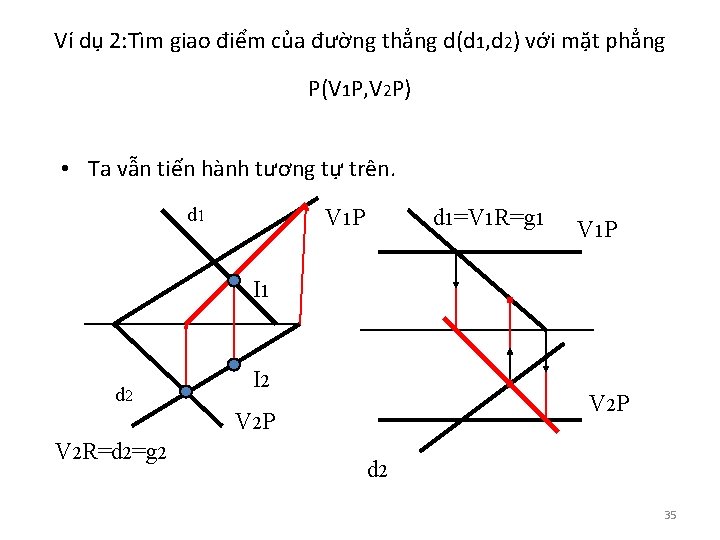
Ví dụ 2: Tìm giao điểm của đường thẳng d(d 1, d 2) với mặt phẳng P(V 1 P, V 2 P) • Ta vẫn tiến hành tương tự trên. d 1 V 1 P d 1=V 1 R=g 1 V 1 P I 1 d 2 I 2 V 2 P V 2 R=d 2=g 2 d 2 35

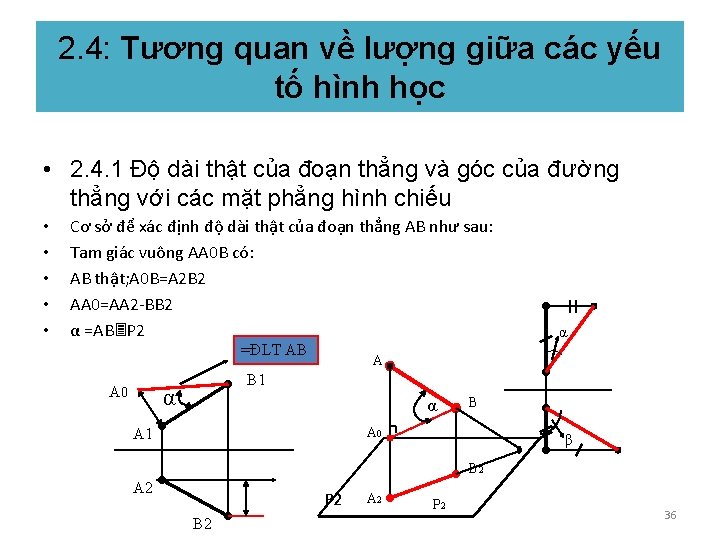
2. 4: Tương quan về lượng giữa các yếu tố hình học • 2. 4. 1 Độ dài thật của đoạn thẳng và góc của đường thẳng với các mặt phẳng hình chiếu • • • Cơ sở để xác định độ dài thật của đoạn thẳng AB như sau: Tam giác vuông AA 0 B có: AB thật; A 0 B=A 2 B 2 AA 0=AA 2 -BB 2 α =AB P 2 =ĐLT AB A 0 α A B 1 α α B A 0 A 1 β B 2 A 2 P 2 36

2. 4. 2 Đường thẳng vuông góc với mặt phẳng-Khoảng cách từ điểm tới mặt phẳng –Từ điểm tới đường thẳng: • Trước khi xét bài toán này ta nhắc lại một số định lý đã biết trong Hình học Không gian: • Định lý 1: Điều kiện cần và đủ để đường thẳng vuông góc với mặt phẳng là đường thẳng đó phải vuông góc với một cặp đường thẳng că t nhau nằm trong mặt phẳng. • Định lý 2: Hình chiếu vuông góc của một góc vuông cũng là một góc vuông khi và chỉ khi góc vuông đó có một cạnh nằm song với mặt phẳng hình chiếu còn cạnh kia không vuông góc với mặt phẳng hình chiếu ấy(định lý này chỉ có trong hình học chiếu). • Kết hợp hai định lý trên trong Hình học Họa hình người ta phát biểu thành định lý sau khi thực hiện trên đồ thư c: • Định lý 3: Đường thẳng h gọi là vuông góc với mặt phẳng P khi h 1 vuông góc với hình chiếu đứng của một đường mặt của mặt phẳng P; và h 2 vuông góc với hình chiếu bằng của một đường bằng của mặt phẳng P. 37

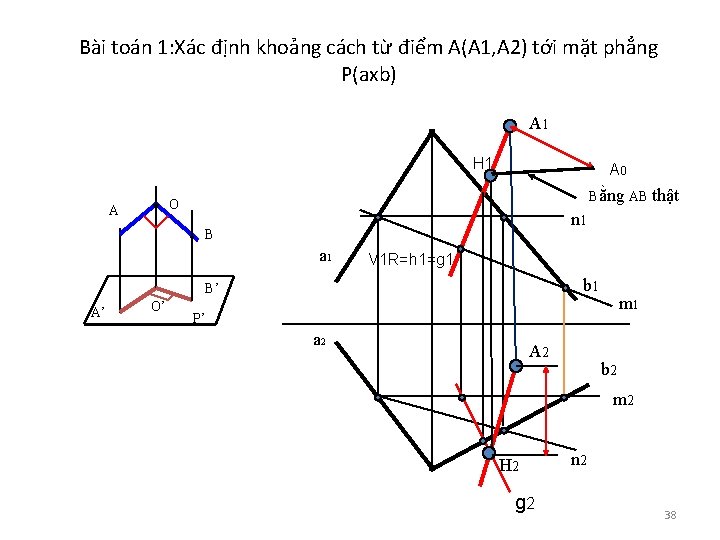
Bài toán 1: Xác định khoảng cách từ điểm A(A 1, A 2) tới mặt phẳng P(axb) A 1 H 1 A 0 Bằng AB thật O A n 1 B a 1 V 1 R=h 1=g 1 b 1 B’ A’ O’ m 1 P’ a 2 A 2 b 2 m 2 H 2 g 2 n 2 38

39

Bài toán 2: Khoảng cách từ điểm tới đường thẳng Như trên ta đã xác định khoảng Cách từ điểm tới mặt phẳng P bằng cách dựng đường thẳng h vuông góc với P. thì ngược lại ta cũng có quyền dựng mặt phẳng P vuông góc với đường thẳng cho trước. Ta xét via dụ sau: Vd: Tìm khoảng cách từ điểm A(A 1, A 2) tới đường thẳng l(l 1, l 2) 40

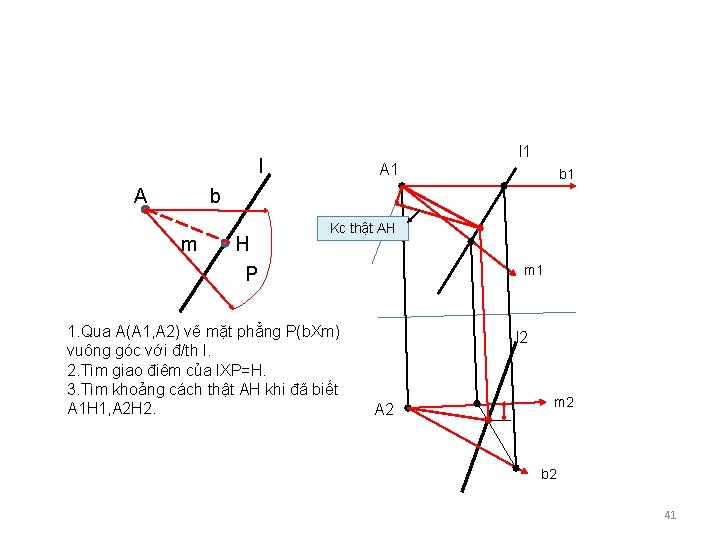
l 1 l A A 1 b m H P Kc thật AH 1. Qua A(A 1, A 2) vẽ mặt phẳng P(b. Xm) vuông góc với đ/th l. 2. Tìm giao điêm của l. XP=H. 3. Tìm khoảng cách thật AH khi đã biết A 1 H 1, A 2 H 2. m 1 l 2 A 2 m 2 b 2 41

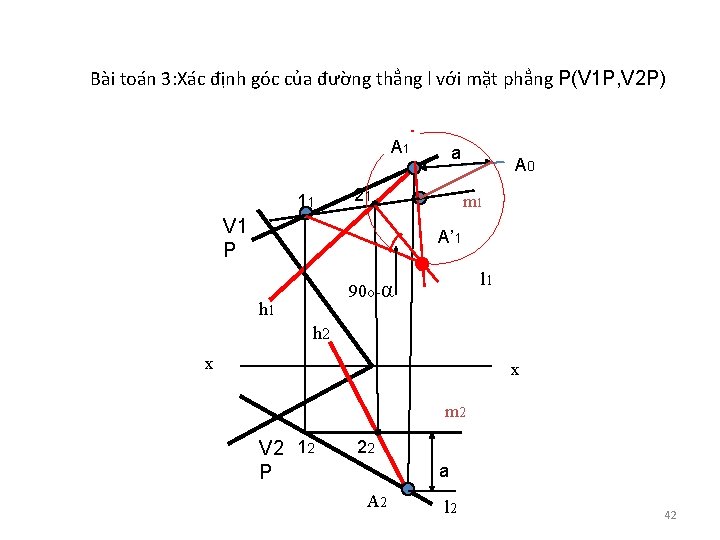
Bài toán 3: Xác định góc của đường thẳng l với mặt phẳng P(V 1 P, V 2 P) A 1 11 a 21 V 1 P A 0 m 1 A’ 1 l 1 90 o-α h 1 h 2 x x m 2 V 2 12 P 22 a A 2 l 2 42

Bài toán 4: Xác định góc của mặt phẳng P với các mặt phẳng hình chiếu. • Giả sử cần xác định góc của mặt phẳng P vơí mặt phẳng hình chiếu bằng P 2. • Cơ sở của phương pháp như sau: • -Trong mặt phẳng P ta vẽ một đường bằng bất kỳ b (Tất nhiên có vô số đường bằng trong mặt phẳng P chúng đều song nhau) • Vẽ đường thẳng d vuông góc với đường bằng b. Hiển nhiên thấy góc của d với P 2 cũng chính là góc của P với mặt phẳng hình chiếu bằng P 2 (d gọi là đường dốc nhất của P với P 2(xem hình vẽ sau) 43

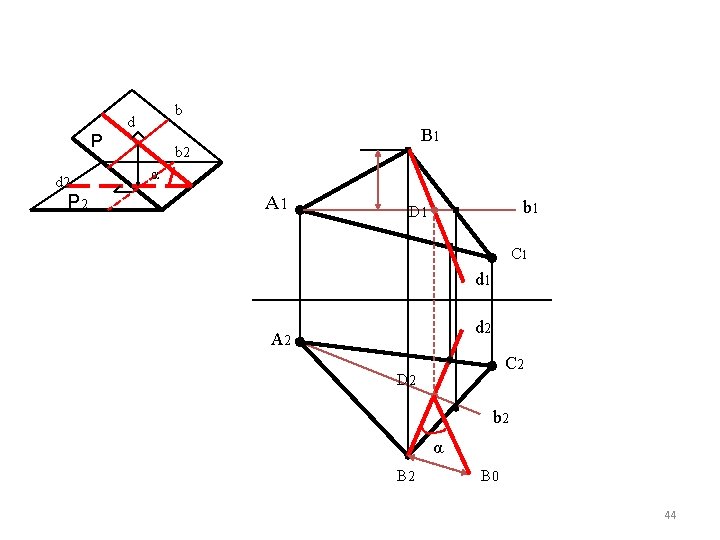
b d P d 2 P 2 B 1 b 2 α A 1 b 1 D 1 C 1 d 2 A 2 C 2 D 2 b 2 α B 2 B 0 44

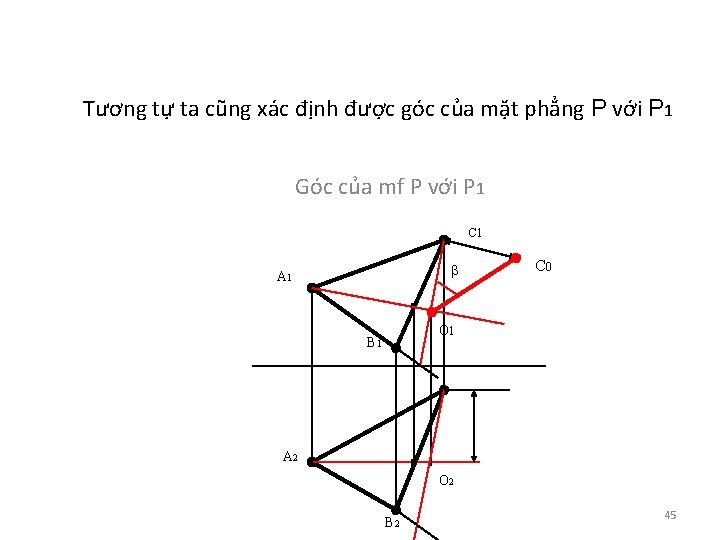
Tương tự ta cũng xác định được góc của mặt phẳng P với P 1 Go c cu a mf P vơ i P 1 C 1 β A 1 C 0 O 1 B 1 A 2 O 2 B 2 45

Chương 2: Biến đổi đồ thức • Trong hình học họa hình thường dùng hai phép biến đổi sau: • 1. Các phép thay mặt phẳng hình chiếu: là các phép biến đổi ta giữ nguyên các đối tượng hình học, chỉ thay đổi vị trí của các mặt phẳng hình chiếu(tất nhiên giữ nguyên các thuộc tính khác của hệ thống). • 2. Các phép dời hình(kể cả những phép dời đặc biệt như quay; gập): Ngược lại giữ nguyên hệ thống mặt phẳng hình chiếu, chỉ thay đổi vị trí các hình 46

2. 1 CÁC PHÉP THAY MẶT PHẲNG HÌNH CHIẾU • Không thể một lúc thay được cả hệ thống hai mặt phẳng hình chiếu, mà phải thay lần lượt từng mặt phẳng một vì khi thay m/f h/c ta phải đảm bảo rằng mặt phẳng h/c bị thay với m/f h/c giữ nguyên vẫn phải vuông góc nhau. • 2. 1. 1 Phép thay mặt phẳng hình chiếu bằng: • Định nghĩa : Thay mặt phẳng hình chiếu bằng là ta tưởng tượng bỏ mặt phẳng hình chiếu bằng cũ , thay bằng mặt phẳng hình chiếu bằng mới ; sao cho mặt phẳng hình chiếu bằng mới vẫn vuông góc với mặt phẳng hình chiếu đứng giữ nguyên. 47

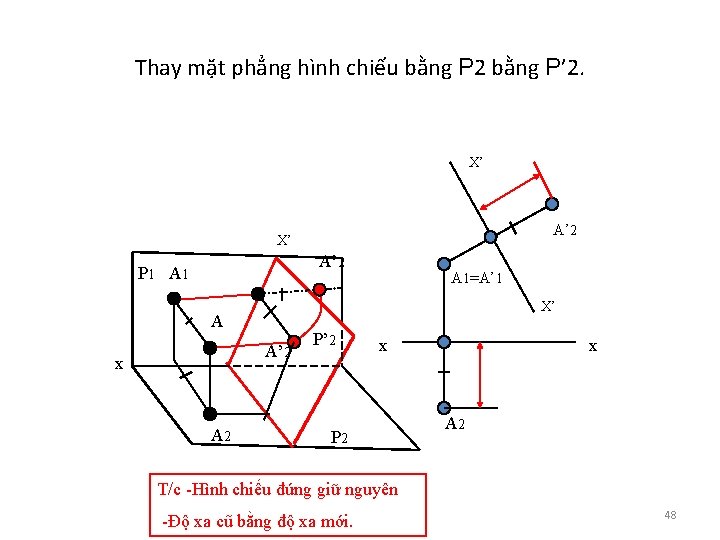
Thay mặt phẳng hình chiếu bằng P 2 bằng P’ 2. X’ A’ 2 P 1 A 1 X’ A A’ 2 x A 2 A 1=A’ 1 P’ 2 x P 2 x A 2 T/c -Hình chiếu đứng giữ nguyên -Độ xa cũ bằng độ xa mới. 48

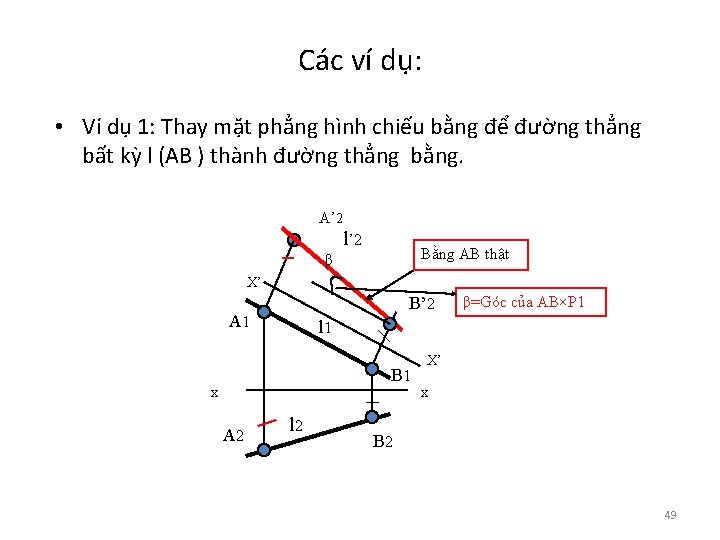
Các ví dụ: • Ví dụ 1: Thay mặt phẳng hình chiếu bằng để đường thẳng bất kỳ l (AB ) thành đường thẳng bằng. A’ 2 l’ 2 Bằng AB thật β X’ B’ 2 A 1 l 1 B 1 x A 2 β=Góc của AB×P 1 l 2 X’ x B 2 49

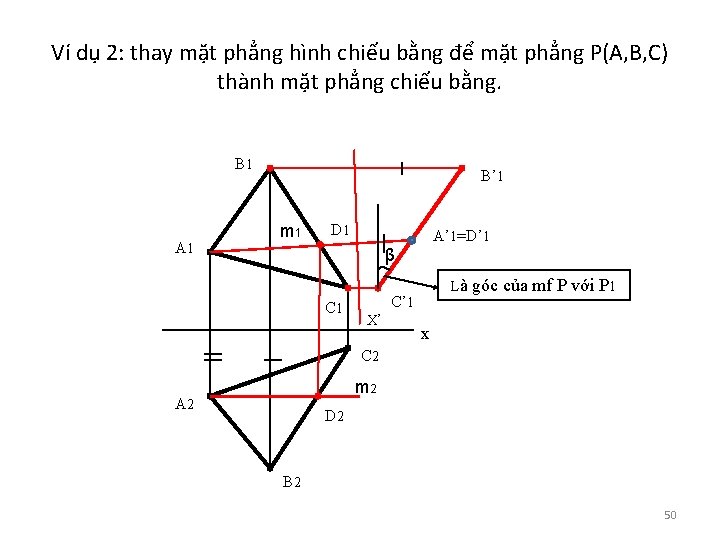
Ví dụ 2: thay mặt phẳng hình chiếu bằng để mặt phẳng P(A, B, C) thành mặt phẳng chiếu bằng. B 1 A 1 B’ 1 m 1 D 1 A’ 1=D’ 1 β C 1 Là C’ 1 X’ góc của mf P với P 1 x C 2 m 2 A 2 D 2 B 2 50

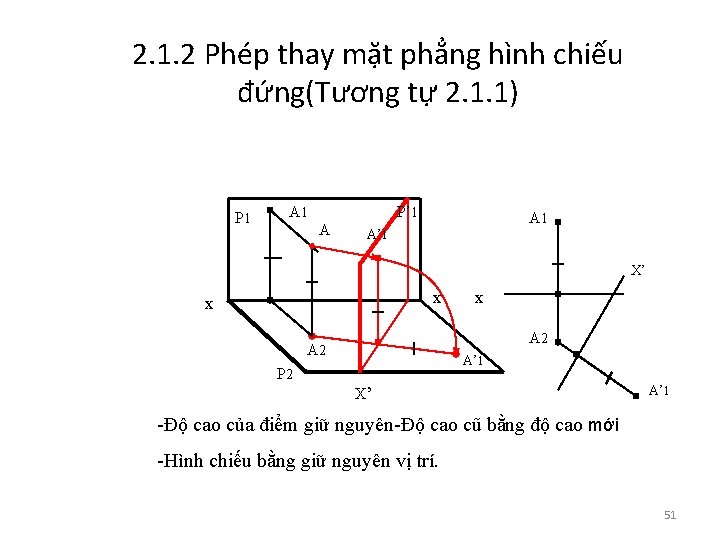
2. 1. 2 Phép thay mặt phẳng hình chiếu đứng(Tương tự 2. 1. 1) P 1 A 1 P’ 1 A A 1 A’ 1 X’ x x x A 2 A’ 1 P 2 X’ A’ 1 -Độ cao của điểm giữ nguyên-Độ cao cũ bằng độ cao mới -Hình chiếu bằng giữ nguyên vị trí. 51

2. 1. 3 Các ví dụ: (cũng tương tự trên) • Ví dụ 1: Thay mặt phẳng hình chiếu đứng để đường thẳng AB bất kỳ thành đường mặt A’ 1 B’ 1=AB (thật) (Hình 1). • Ví dụ 2: Thay mặt phẳng hình chiếu đứng để mặt phẳng P(ABC) thành mặt phẳng chiếu đứng. (Hình 2) 52

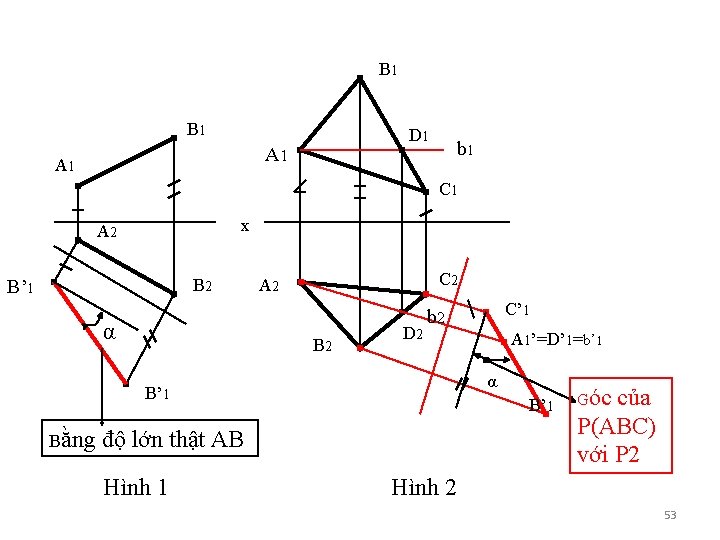
B 1 D 1 A 1 b 1 C 1 x A 2 B’ 1 α C 2 A 2 B 2 D 2 B’ 1 độ lớn thật AB Hình 1 A 1’=D’ 1=b’ 1 α B’ 1 Bằng C’ 1 b 2 Góc của P(ABC) với P 2 Hình 2 53

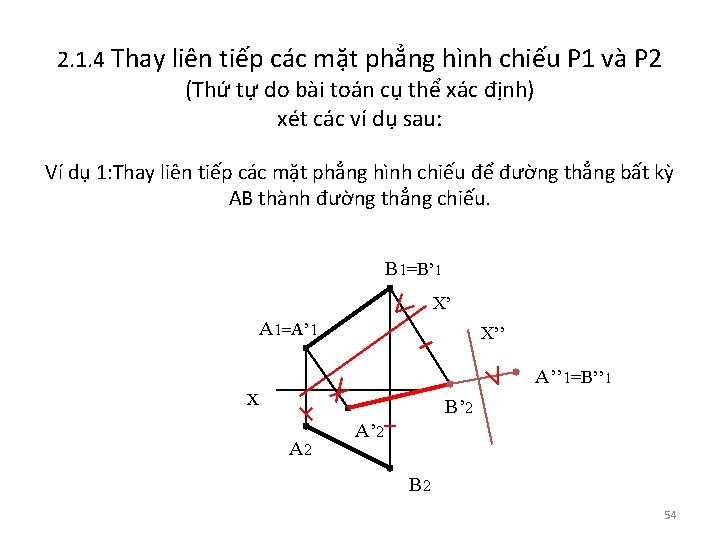
2. 1. 4 Thay liên tiếp các mặt phẳng hình chiếu P 1 và P 2 (Thứ tự do bài toán cụ thể xác định) xét các ví dụ sau: Ví dụ 1: Thay liên tiếp các mặt phẳng hình chiếu để đường thẳng bất kỳ AB thành đường thẳng chiếu. B 1=B’ 1 X’ A 1=A’ 1 X’’ A’’ 1=B’’ 1 x B’ 2 A’ 2 B 2 54

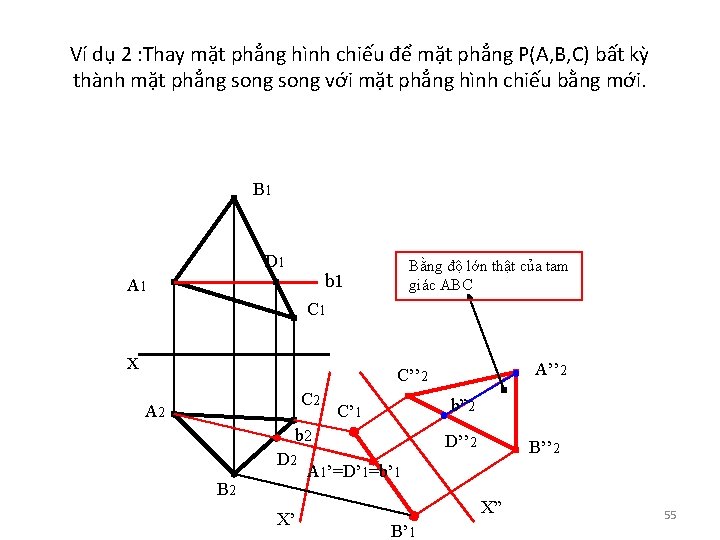
Ví dụ 2 : Thay mặt phẳng hình chiếu để mặt phẳng P(A, B, C) bất kỳ thành mặt phẳng song với mặt phẳng hình chiếu bằng mới. B 1 D 1 Bằng độ lớn thật của tam giác ABC b 1 A 1 C 1 x A’’ 2 C 2 A 2 b” 2 C’ 1 b 2 D 2 B 2 X’ D’’ 2 B’’ 2 A 1’=D’ 1=b’ 1 X” B’ 1 55

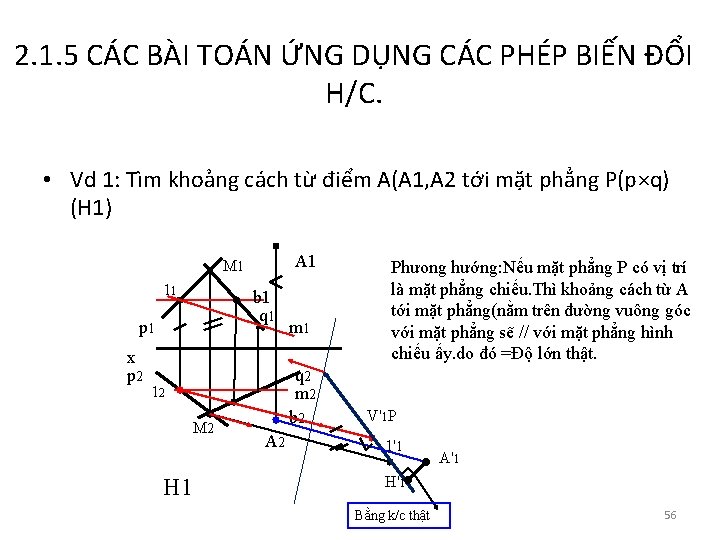
2. 1. 5 CÁC BÀI TOÁN ỨNG DỤNG CÁC PHÉP BIẾN ĐỔI H/C. • Vd 1: Tìm khoảng cách từ điểm A(A 1, A 2 tới mặt phẳng P(p×q) (H 1) A 1 M 1 11 b 1 q 1 p 1 x p 2 q 2 m 2 b 2 12 M 2 H 1 m 1 A 2 Phưong hướng: Nếu mặt phẳng P có vị trí là mặt phẳng chiếu. Thì khoảng cách từ A tới mặt phẳng(nằm trên đường vuông góc với mặt phẳng sẽ // với mặt phẳng hình chiếu ấy. do đó =Độ lớn thật. V'1 P 1'1 A'1 H'1 Bằng k/c thật 56

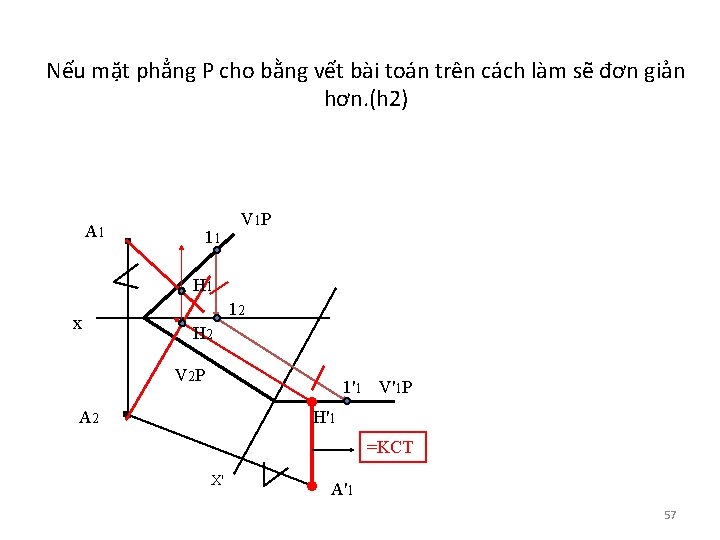
Nếu mặt phẳng P cho bằng vết bài toán trên cách làm sẽ đơn giản hơn. (h 2) A 1 11 V 1 P H 1 x 12 H 2 V 2 P 1'1 V'1 P A 2 H'1 =KCT X' A'1 57

Vd 2: Tìm góc nhị diện của hai mặt phẳng P(ABC) và Q(ABD) (h 3) • Trong mọi trường hợp để tìm góc nhị diện của hai mặt phẳng ta đều phải thực hiện các bước sau: • 1. Tìm giao tuyến g của hai mặt phẳng. • 2. Dựng góc phẳng của nhị diện tại một điểm nào đó trên giao tuyến. (mặt phẳng của nhị diệnvuông góc với giao tuyến. • 3. Xác định các cạnh của góc phẳng. • 4. Nếu góc phẳng này không song với mặt phẳng hình chiếu, thì phải tìm độ lớn thật của góc phẳng đó!Nếu ta dùng các phép biến đổi h/c ta có thể rút ngắn các bước giải trên rất nhiều! 58

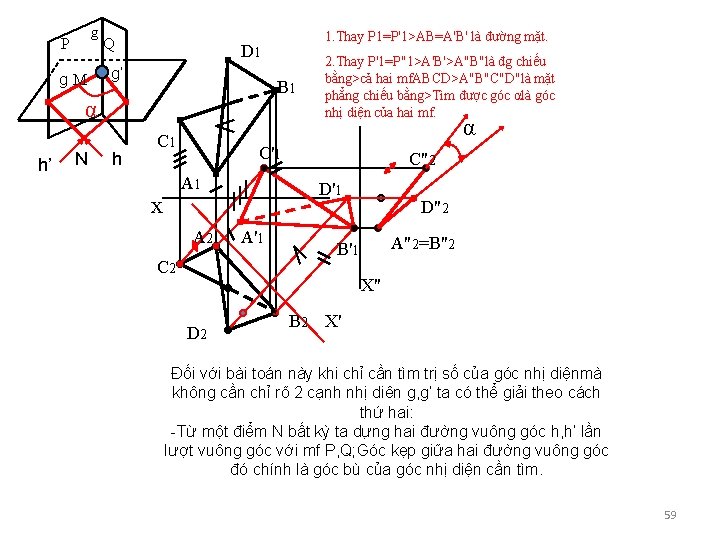
g P g. M Q D 1 g’ B 1 α h’ N h 1. Thay P 1=P'1>AB=A'B' là đường mặt. α C 1 C'1 A 1 x 2. Thay P'1=P"1>A'B'>A"B"là đg chiếu bằng>cả hai mf. ABCD>A"B"C"D"là mặt phẳng chiếu bằng>Tìm được góc αlà góc nhị diện của hai mf. A 2 C"2 D'1 A'1 D"2 A"2=B"2 B'1 X" D 2 B 2 X' Đối với bài toán này khi chỉ cần tìm trị số của góc nhị diệnmà không cần chỉ rõ 2 cạnh nhị diên g, g’ ta có thể giải theo cách thứ hai: -Từ một điểm N bất kỳ ta dựng hai đường vuông góc h, h’ lần lượt vuông góc với mf P, Q; Góc kẹp giữa hai đường vuông góc đó chính là góc bù của góc nhị diện cần tìm. 59

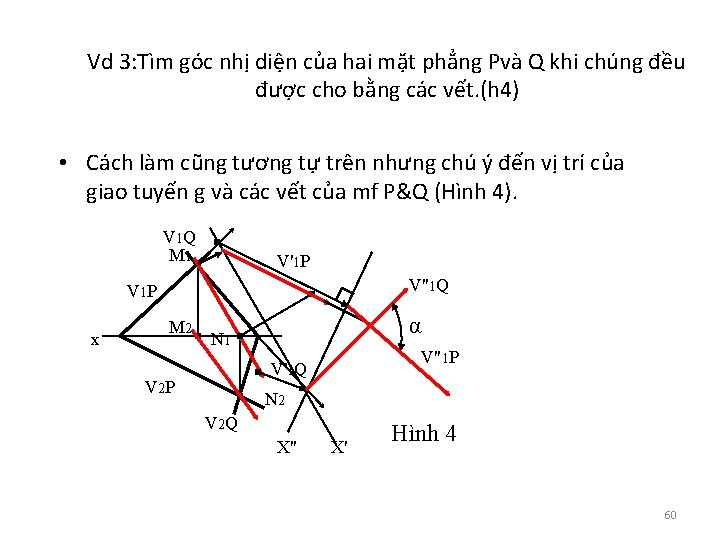
Vd 3: Tìm góc nhị diện của hai mặt phẳng Pvà Q khi chúng đều được cho bằng các vết. (h 4) • Cách làm cũng tương tự trên nhưng chú ý đến vị trí của giao tuyến g và các vết của mf P&Q (Hình 4). V 1 Q M 1 V'1 P V''1 Q V 1 P x M 2 α N 1 V"1 P V'1 Q V 2 P N 2 V 2 Q X" X' Hình 4 60

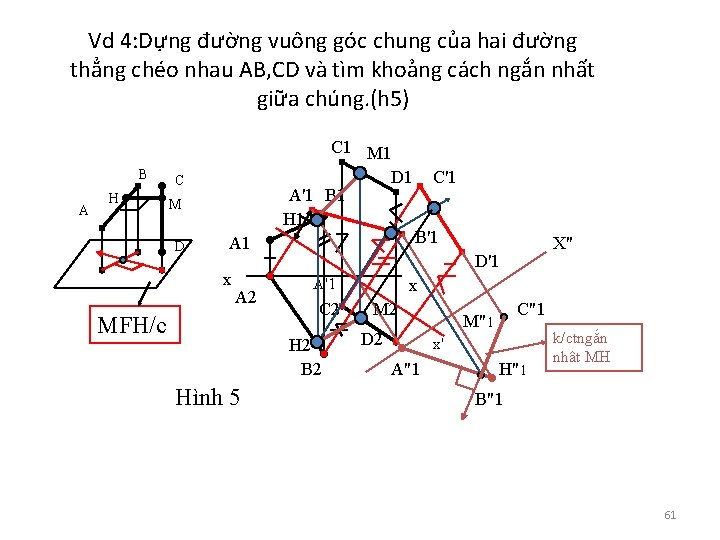
Vd 4: Dựng đường vuông góc chung của hai đường thẳng chéo nhau AB, CD và tìm khoảng cách ngắn nhất giữa chúng. (h 5) B A H C 1 M 1 D 1 A'1 B 1 H 1 C M D A 1 x A 2 MFH/c B'1 X'' D'1 A'1 C 2 H 2 B 2 Hình 5 C'1 x M 2 D 2 C"1 M"1 x' A"1 H"1 k/ctngắn nhât MH B"1 61

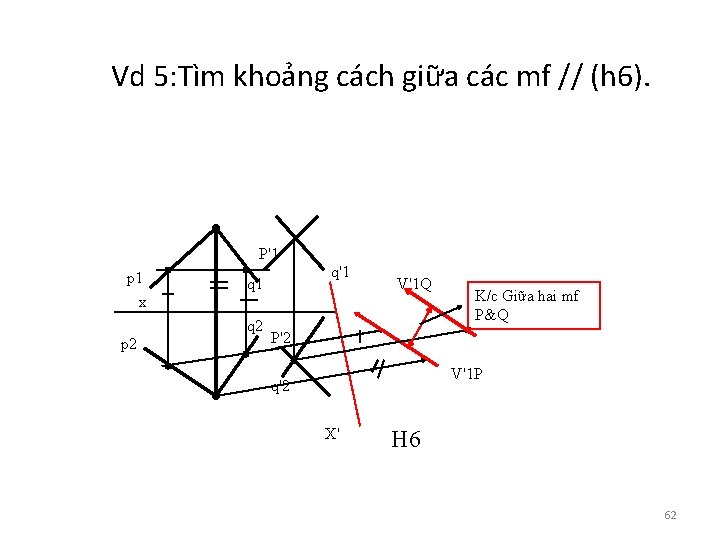
Vd 5: Tìm khoảng cách giữa các mf // (h 6). P'1 p 1 x q 2 p 2 q'1 q 1 V'1 Q K/c Giữa hai mf P&Q P'2 V'1 P q'2 X' H 6 62

2. 2 CÁC PHÉP DỜI HÌNH • Dời một hình là ta di chuyển hình đến vị trí mới mà vẫn giữ nguyên vị trí các mặt phẳng hình chiếu. Trong quá trình dời hình Ø=Ø'. Nên người ta nói rằng: "phép dời bảo tồn khoảng cách giữa các yếu tố của hình" • Ta có định nghĩa như sau: 63

• Dơ i hình Ø đến vị trí Ø' là một phép biến hình 1 -1 sao cho nó bảo tồn khoảng cách giữa hai điểm bất kỳ của Ø và Ø'. • Trong hình học hoạ hình người ta chỉ áp dụng các phép dời mà đường thẳng nối các điểm tương ứng //với các mặt phẳng hi nh chiê u. Gọi là các phép dời hình song phẳng. • . Thường là // với P 1 hoặc P 2. 64

2. 2. 1 Phép dời hình song với P 2: • Đn: là phép dời mà các điểm tương ứng của Ø và Ø' đều // với P 1. A 1 A'1; B 1 B'1…//P 1(có nghĩa là các đường thẳng đó đều là đường mặt). Dễ dàng thấy phép dời này có các t/c sau: 1. A 2 B 2=A'2 B'2(h/c bằng cũ bằng h/c bằng mới) 2. A 1 A'1; B 1, B'1//xx(AA'; B B' là những đường bằng) B B' B 0 B'0 A' A A 2 B'2 A'2 65

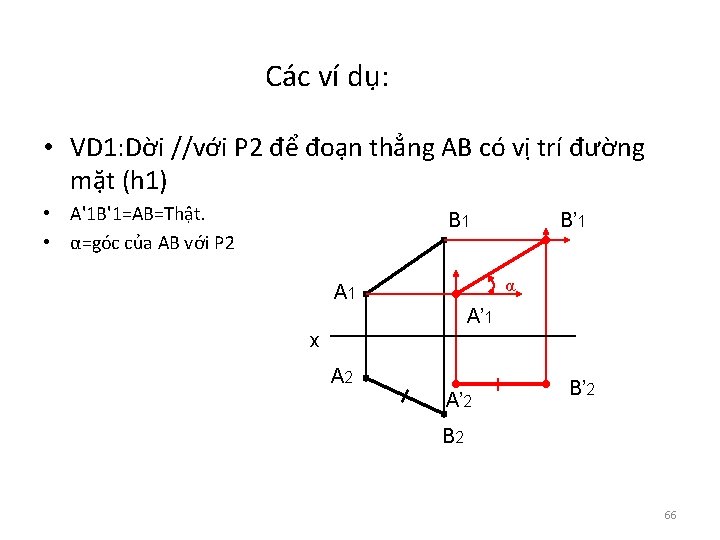
Các ví dụ: • VD 1: Dời //với P 2 để đoạn thẳng AB có vị trí đường mặt (h 1) • A'1 B'1=AB=Thật. • α=góc của AB với P 2 B 1 B’ 1 α A 1 A’ 1 x A 2 A’ 2 B 2 66

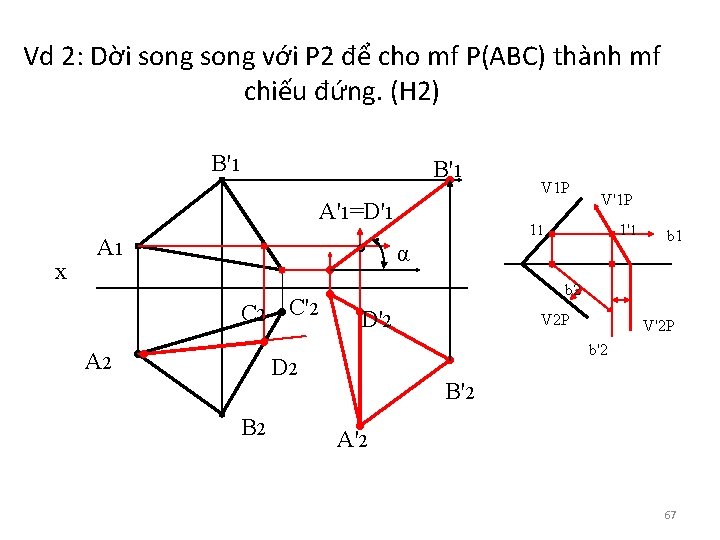
Vd 2: Dời song với P 2 để cho mf P(ABC) thành mf chiếu đứng. (H 2) B'1 A'1=D'1 x A 1 V 1 P V'1 P 11 1'1 α C 2 C'2 A 2 b 2 D'2 V 2 P V'2 P b'2 D 2 B 2 b 1 B'2 A'2 67

• 2. 2. 2 Dời // với P 1: • Là phép dời mà đường thẳng nối các điểm tương ứng đều // với P 1(AA'; BB'…//với P 1(di chuyển theo những đường mặt). • Tc 1: A 1 B 1=A'1 B'1… • Tc 2: A 2 B 2//xx • Và cũng tương tự trên ta có thể dời cho đường thẳng bất kỳ thành đường bằng; mf bất kỳ thành mặt phẳng chiếu bằng. • Sinh viên tự vẽ hình. 68

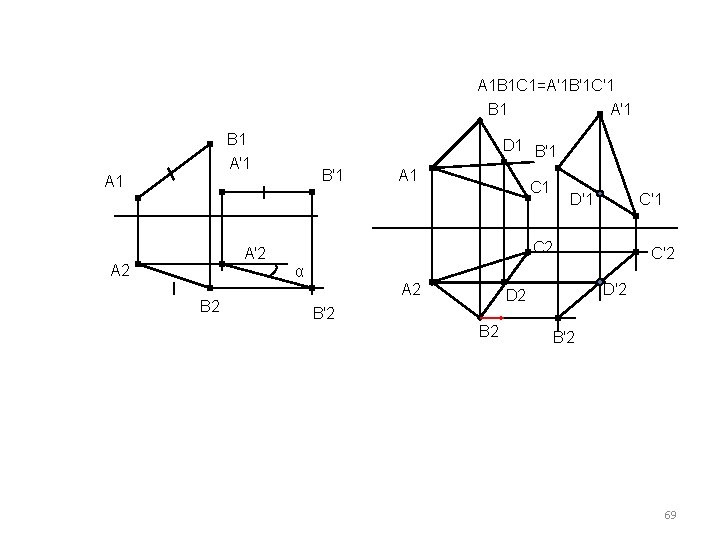
A 1 B 1 C 1=A'1 B'1 C'1 B 1 A'1 D 1 B'1 A 1 C 1 C'1 C 2 A'2 A 2 D'1 C'2 α B 2 A 2 D'2 D 2 B'2 B 2 B'2 69

2. 2. 3 Dời hình liên tiếp //với các mf hc: • Nhiều bài toán hh phức tạp để có kết quả ta cần dời liên tiếp song với nhiều mf h/c. Thứ tự các phép dời do yêu cầu của từng bài toán cụ thể. • Các ví dụ: • Vd 1: Tìm độ lớn thật của tam giác ABC. • Để tìm độ lớn thật của tam giác ABC ta cần thực hiện 2 phép dời liên tiếp: • -Dời cho mf của tg thành mf chiếu. • -Dời tiếp cho mf tg thành mf// với mfhc còn lại. (hình 1). 70

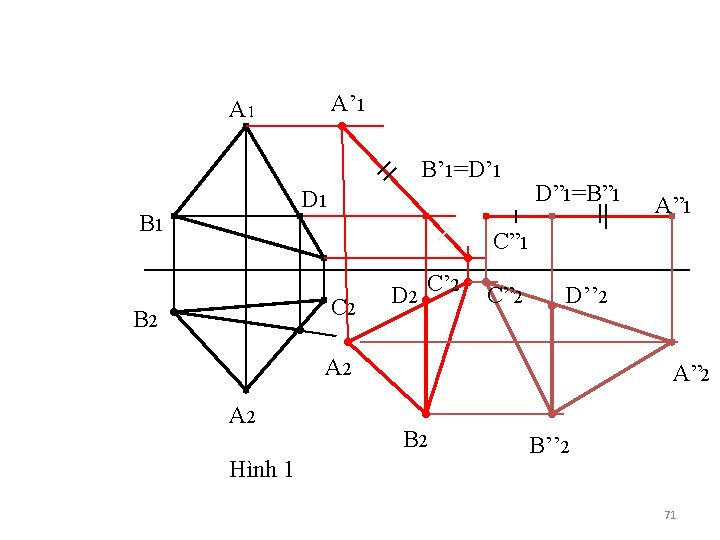
A’ 1 A 1 B’ 1=D’ 1 D 1 B 1 D” 1=B” 1 A” 1 C 2 B 2 D 2 C’ 2 C” 2 D’’ 2 A 2 Hình 1 A” 2 B’’ 2 71

2. 3. CÁC PHÉP QUAY-GẬP • 1. 1 Phép quay quanh một trục: • Các phép quay, gập thực chất chúng chỉ là một trường hợp đặc biệt của các phép dời hình mà thôi khi ta cố định một số yếu tố nào đó của hình. Trở lại phép dời đường thăng AB ở trên. Khi ta cố định điểm A bằng một trục thẳng đứng đi qua A chẳng hạn, để có vị trí nào đó của hình ta chỉ việc quay điểm B đi một góc α. • Tùy theo vị trí trục quay mà ta có • Phép quay khác nhau: • Nếu trục quay là đường thẳng chiếu có phép quay quanh đường thẳng chiếu; Nếu trục quay là các đường đồng mức-có các phép quay các đường đồng mức(đ/bằng, đường mặt); nếu trục quay là các vêt-có các phép quay quanh các vết hay còn gọi là các phép gập mặt phẳng quanh các vết của nó(thực chất vết của mặt phẳng cũng chỉ là các đường bằng hay đường mặt đặc biệt mà thôi-Vì vậy đây cũng chỉ là các phép quay quanh các đường thẳng đồng mức) 72

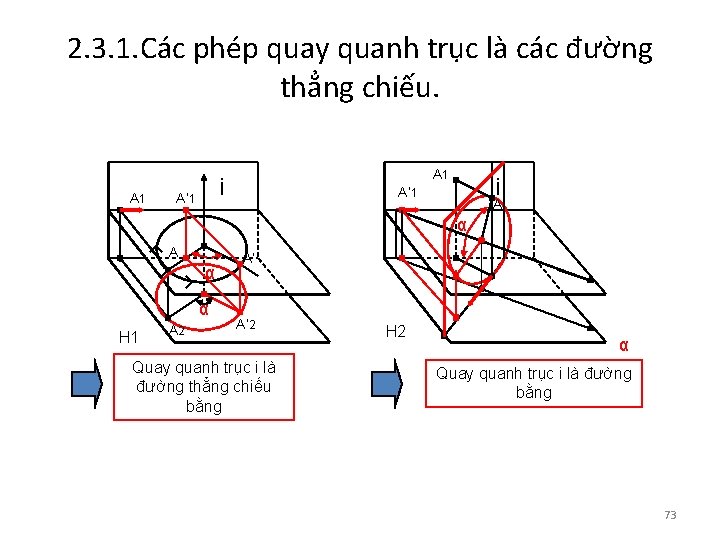
2. 3. 1. Các phép quay quanh trục là các đường thẳng chiếu. A 1 i A’ 1 A α α H 1 A 2 A’ A’ 2 Quay quanh trục i là đường thẳng chiếu bằng H 2 α Quay quanh trục i là đường bằng 73

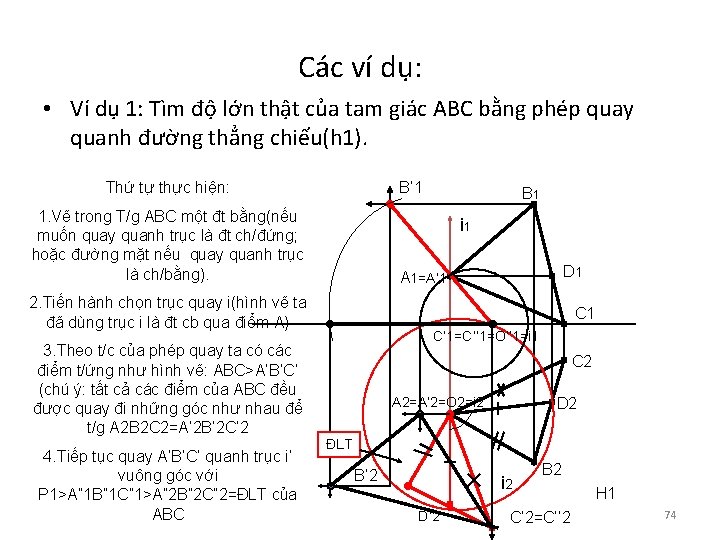
Các ví dụ: • Ví dụ 1: Tìm độ lớn thật của tam giác ABC bằng phép quay quanh đường thẳng chiếu(h 1). Thứ tự thực hiện: B’ 1 1. Vẽ trong T/g ABC một đt bằng(nếu muốn quay quanh trục là đt ch/đứng; hoặc đường mặt nếu quay quanh trục là ch/bằng). i 1 D 1 A 1=A’ 1 2. Tiến hành chọn trục quay i(hình vẽ ta đã dùng trục i là đt cb qua điểm A) C 1 C’ 1=C’’ 1=O’’ 1=i 1 3. Theo t/c của phép quay ta có các điểm t/ứng như hình vẽ: ABC>A’B’C’ (chú ý: tất cả các điểm của ABC đều được quay đi những góc như nhau để t/g A 2 B 2 C 2=A’ 2 B’ 2 C’ 2 4. Tiếp tục quay A’B’C’ quanh trục i’ vuông góc với P 1>A” 1 B” 1 C” 1>A” 2 B” 2 C” 2=ĐLT của ABC B 1 C 2 A 2=A’ 2=O 2=i 2 D 2 ĐLT B’ 2 i 2 D’ 2 B 2 C’ 2=C’’ 2 H 1 74

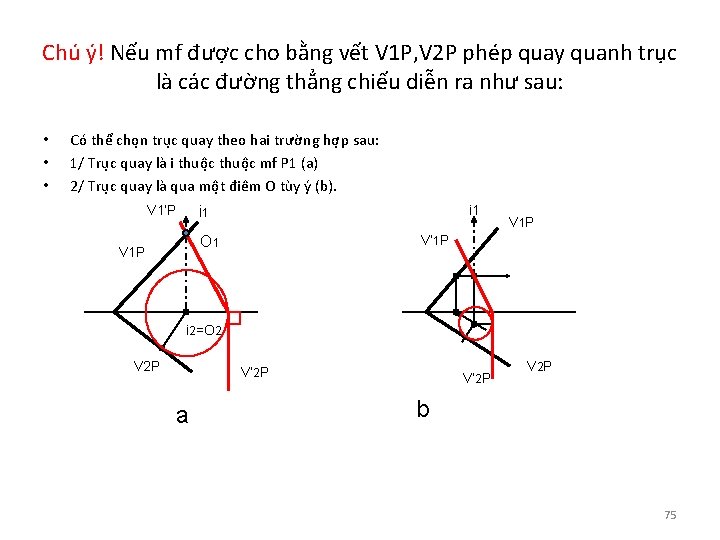
Chú ý! Nếu mf được cho bằng vết V 1 P, V 2 P phép quay quanh trục là các đường thẳng chiếu diễn ra như sau: • • • Có thể chọn trục quay theo hai trường hợp sau: 1/ Trục quay là i thuộc mf P 1 (a) 2/ Trục quay là qua một điêm O tùy ý (b). V 1’P i 1 V’ 1 P O 1 V 1 P i 2=O 2 V 2 P V’ 2 P a V’ 2 P V 2 P b 75

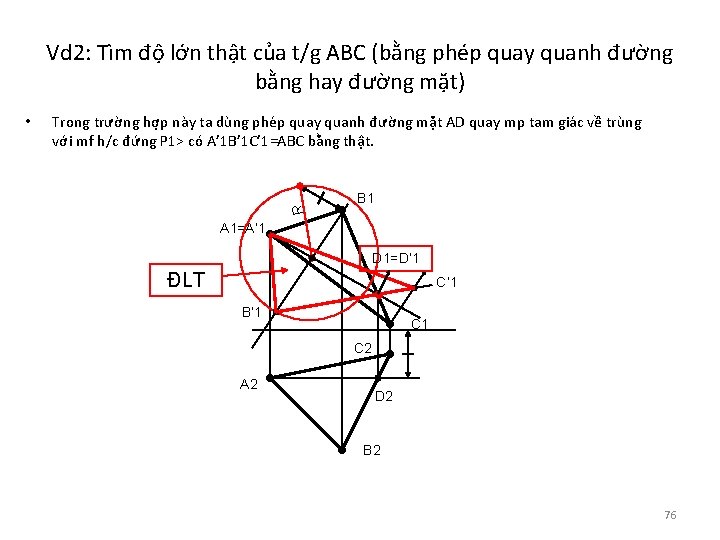
Vd 2: Tìm độ lớn thật của t/g ABC (bằng phép quay quanh đường bằng hay đường mặt) Trong trường hợp này ta dùng phép quay quanh đường mặt AD quay mp tam giác về trùng với mf h/c đứng P 1> có A’ 1 B’ 1 C’ 1=ABC bằng thật. R • B 1 A 1=A’ 1 D 1=D’ 1 ĐLT C’ 1 B’ 1 C 2 A 2 D 2 B 2 76

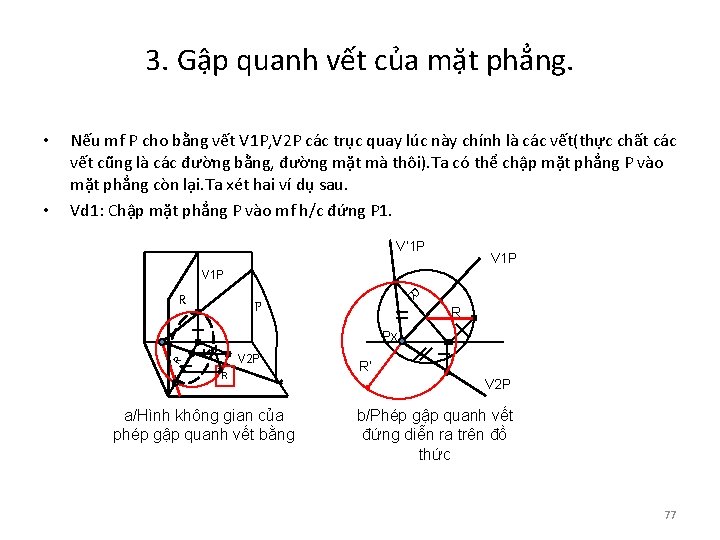
3. Gập quanh vết của mặt phẳng. • Nếu mf P cho bằng vết V 1 P, V 2 P các trục quay lúc này chính là các vết(thực chất các vết cũng là các đường bằng, đường mặt mà thôi). Ta có thể chập mặt phẳng P vào mặt phẳng còn lại. Ta xét hai ví dụ sau. Vd 1: Chập mặt phẳng P vào mf h/c đứng P 1. V’ 1 P V 1 P R R Px V 2 P R • R a/Hình không gian của phép gập quanh vết bằng R’ V 2 P b/Phép gập quanh vết đứng diễn ra trên đồ thức 77

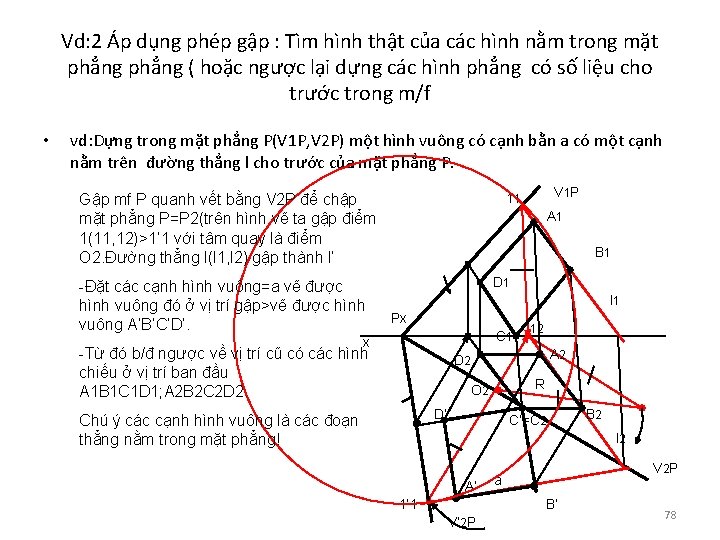
Vd: 2 Áp dụng phép gập : Tìm hình thật của các hình nằm trong mặt phẳng ( hoặc ngược lại dựng các hình phẳng có số liệu cho trước trong m/f • vd: Dựng trong mặt phẳng P(V 1 P, V 2 P) một hình vuông có cạnh bằn a có một cạnh nằm trên đường thẳng l cho trước của mặt phẳng P. -Đặt các cạnh hình vuông=a vẽ được hình vuông đó ở vị trí gập>vẽ được hình vuông A’B’C’D’. V 1 P 11 Gập mf P quanh vết bằng V 2 P để chập mặt phẳng P=P 2(trên hình vẽ ta gập điểm 1(11, 12)>1’ 1 với tâm quay là điểm O 2. Đường thẳng l(l 1, l 2) gập thành l’ A 1 B 1 D 1 l 1 Px C 1 x -Từ đó b/đ ngược về vị trí cũ có các hình chiếu ở vị trí ban đầu A 1 B 1 C 1 D 1; A 2 B 2 C 2 D 2. 12 A 2 D 2 R O 2 D’ Chú ý các cạnh hình vuông là các đoạn thẳng nằm trong mặt phẳng! C’=C 2 B 2 l 2 A’ 1’ 1 V 2 P a B’ V’ 2 P 78

Câu hỏi và bài tập ứng dụng các phép biến đổi đồ thức. • 1. Tại sao nói phép dời hình là tích của hai phép tịnh tiến và phép quay? • 2. Phép dời hình có các tính chất cơ bản gì? • 3. Tại sao người ta không thể thay một lúc cả hai mặt phẳng hình chiếu? • Hãy cho biết tiện ích và phạm vi ứng dụng có lợi nhất mà mỗi phép biến đổi mang lại? • Bài tập: ứng dụng các phép biến đổi h/c: 1. Tìm độ lớn thật của tam giác ABC(A 1 B 1 C 1, A 2 B 2 C 2) Nên dùng phép biến đổi nào là có lợi nhất? 2. Tìm góc của mặt phẳng P cho bất kỳ; và mặt phẳng P cho bởi các vết với các mf hình chiếu. 3. Tìm khoảng cách từ một điểm A(A 1, A 2) tới mặt phẳng P: • a/ Mặt phẳng P cho bằng các yếu tố bất kỳ xác định nó. • b/ Mặt phẳng P cho bởi hai vết của nó. 4. Tìm khoảng cách từ một điểm A(A 1, A 2) bất kỳ đến đ/thẳng l(l 1, l 2) cho trước. 5. Tìm k/c ngắn nhất giữa hai đ/thẳng song nhau a, b cho trước 6. Tìm khoảng cách ngắn nhất giữa hai đường thẳng chéo nhau a, b. 7. Tìm khoảng cách giữa hai mf P(axb) và Q(cxd) kể cả trường hợp một trong hai mặt phẳng đều cho bằng các vết của chúng. 8. Tìm góc của đường thẳng l đã cho với mặt phẳng P bất kỳ và mặt phẳng P cho bởi các vết. 9. Tìm góc nhị diện của hai mặt phẳng bất kỳ P, Q kể cả trường hợp hai mặt phẳng P, Q đều cho bằng các vết. 10. Vẽ đường vuông góc chung của hai đường thẳng chéo nhau AB, CD cho trước và tìm khoảng cách ngắn nhất giữa chúng. 11. Dựng một hình nón tròn xoay có đáy là vòng tròn thuộc bán kính bằng R cho trước có tâm là điểm O cho trước nằm trong mf P(V 1 P, V 2 P), có chiều cao bằng h cho trước. Hết 79

80

81

82

83

84

85

86

cong họ xycloid… 87

88