Ton Hnh tam gic a Hnh tam gic

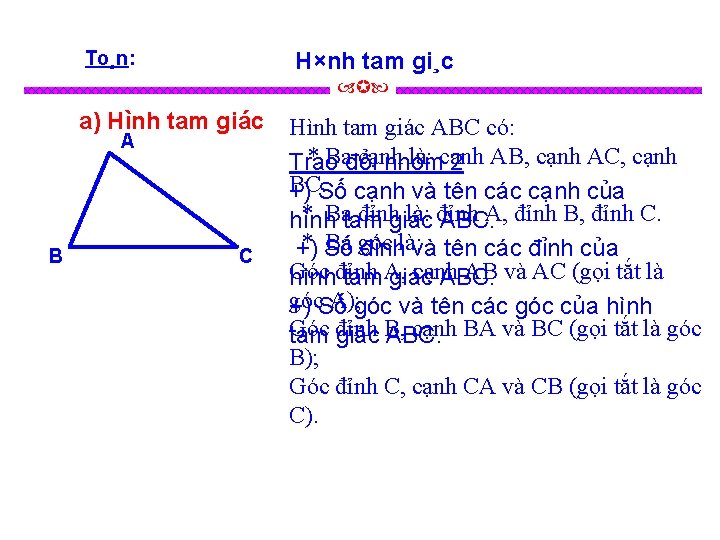
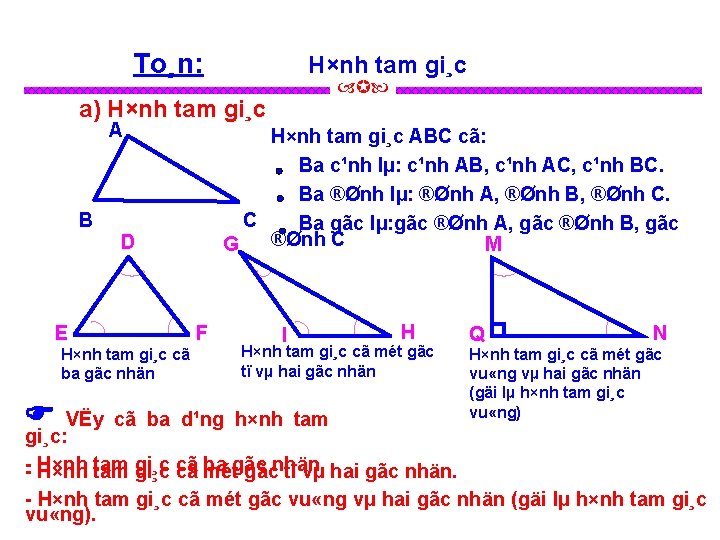
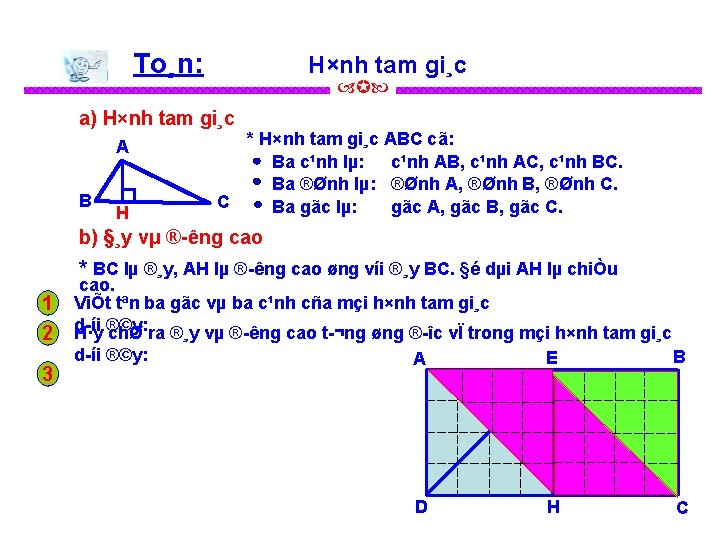
To¸n: H×nh tam gi¸c a) Hình tam giác A B C Hình tam giác ABC có: * Bađổi cạnh là: cạnh Trao nhóm 2 AB, cạnh AC, cạnh BC. +) Số cạnh và tên các cạnh của * Batam đỉnhgiác là: đỉnh hình ABC. A, đỉnh B, đỉnh C. * Số Ba góc +) đỉnhlà: và tên các đỉnh của Góc cạnh AB và AC (gọi tắt là hìnhđỉnh tam A, giác ABC. góc A); góc và tên các góc của hình +) Số Góc cạnh BA và BC (gọi tắt là góc tam đỉnh giác B, ABC. B); Góc đỉnh C, cạnh CA và CB (gọi tắt là góc C).

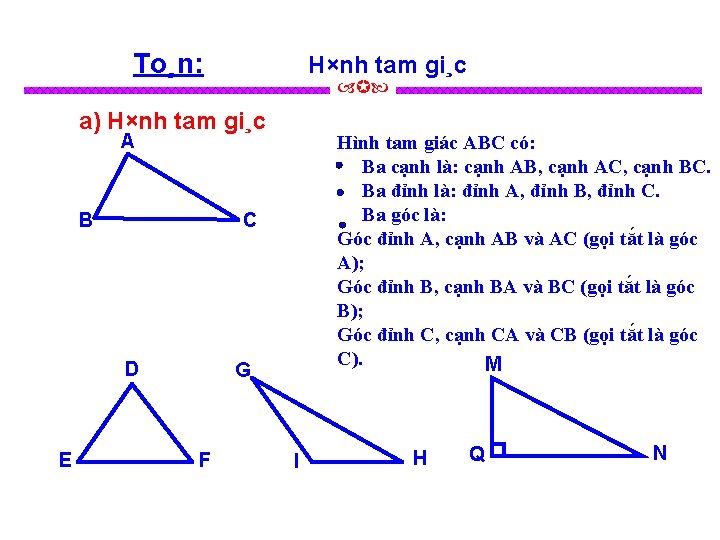
To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A B C D E Hình tam giác ABC có: Ba cạnh là: cạnh AB, cạnh AC, cạnh BC. Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C. Ba góc là: Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A); Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B); Góc đỉnh C, cạnh CA và CB (gọi tắt là góc C). M G F I H Q N

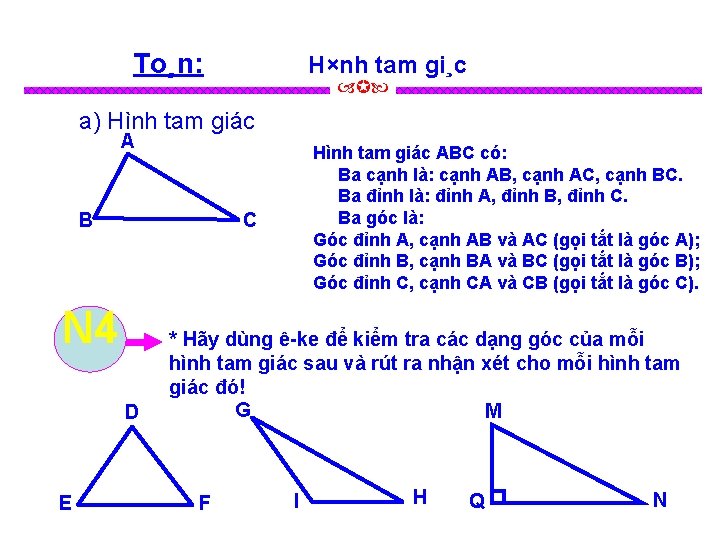
To¸n: H×nh tam gi¸c a) Hình tam giác A B C N 4 D E Hình tam giác ABC có: Ba cạnh là: cạnh AB, cạnh AC, cạnh BC. Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C. Ba góc là: Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A); Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B); Góc đỉnh C, cạnh CA và CB (gọi tắt là góc C). * Hãy dùng ê ke để kiểm tra các dạng góc của mỗi hình tam giác sau và rút ra nhận xét cho mỗi hình tam giác đó! G M F I H Q N

To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A B D E H×nh tam gi¸c cã ba gãc nhän H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc ®Ønh A, gãc ®Ønh B, gãc ®Ønh C G M F I H H×nh tam gi¸c cã mét gãc tï vµ hai gãc nhän VËy cã ba d¹ng h×nh tam gi¸c: H×nh tam gi¸c cã cã ba métgãc gãcnhän. tï vµ hai gãc nhän. Q N H×nh tam gi¸c cã mét gãc vu «ng vµ hai gãc nhän (gäi lµ h×nh tam gi¸c vu «ng).

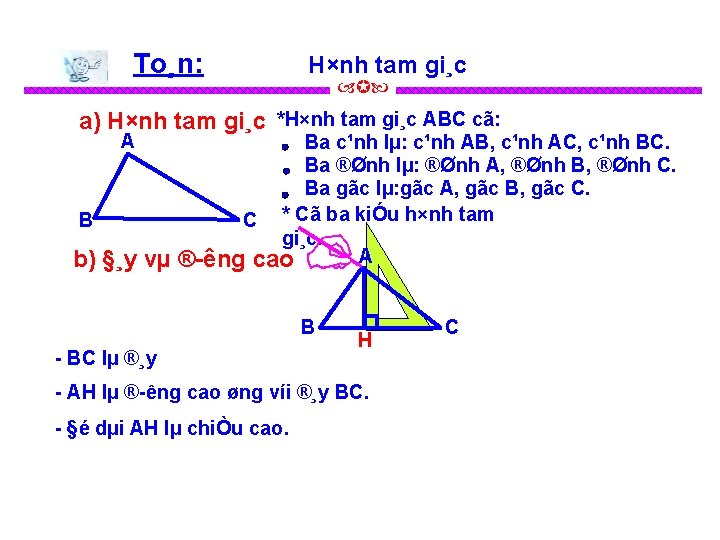
To¸n: H×nh tam gi¸c a) H×nh tam gi¸c *H×nh tam gi¸c ABC cã: A B b) §¸y vµ Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. Ba gãc lµ: gãc A, gãc B, gãc C. C * Cã ba kiÓu h×nh tam gi¸c. A ® êng cao B BC lµ ®¸y H AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu cao. C

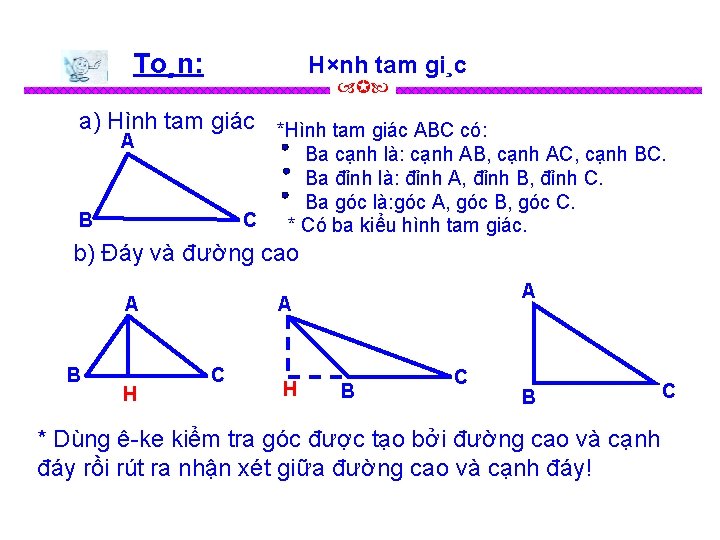
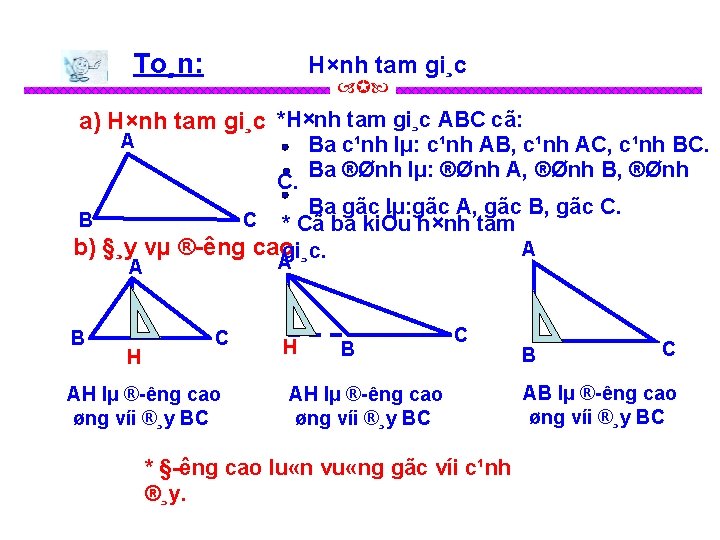
To¸n: H×nh tam gi¸c a) Hình tam giác *Hình tam giác ABC có: A B C Ba cạnh là: cạnh AB, cạnh AC, cạnh BC. Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C. Ba góc là: góc A, góc B, góc C. * Có ba kiểu hình tam giác. b) Đáy và đường cao B H A A A C H B C B * Dùng ê-ke kiểm tra góc được tạo bởi đường cao và cạnh đáy rồi rút ra nhận xét giữa đường cao và cạnh đáy! C

To¸n: H×nh tam gi¸c a) H×nh tam gi¸c *H×nh tam gi¸c ABC cã: A C. Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh Ba gãc lµ: gãc A, gãc B, gãc C. * Cã ba kiÓu h×nh tam b) §¸y vµ ® êng caogi¸c. A B C A A B H C AH lµ ® êng cao øng víi ®¸y BC H B C AH lµ ® êng cao øng víi ®¸y BC * § êng cao lu «n vu «ng gãc víi c¹nh ®¸y. B C AB lµ ® êng cao øng víi ®¸y BC

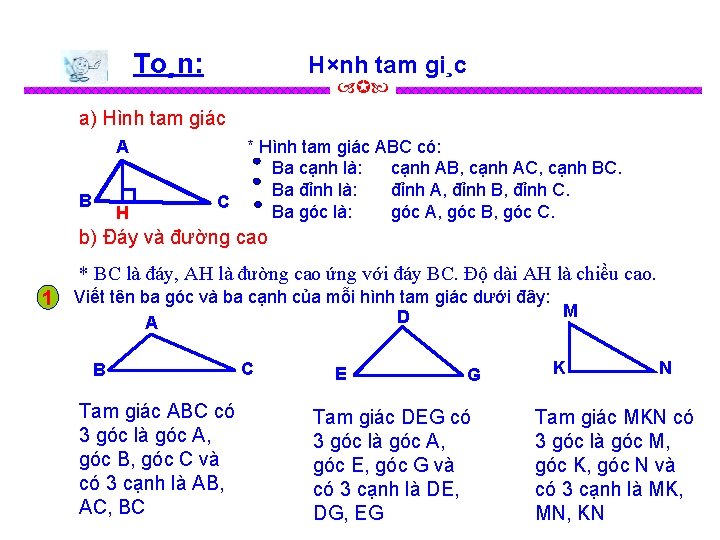
To¸n: H×nh tam gi¸c a) Hình tam giác A B H * Hình tam giác ABC có: Ba cạnh là: cạnh AB, cạnh AC, cạnh BC. Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C. C Ba góc là: góc A, góc B, góc C. b) Đáy và đường cao * BC là đáy, AH là đường cao ứng với đáy BC. Độ dài AH là chiều cao. 1 Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây: M D A B Tam giác ABC có 3 góc là góc A, góc B, góc C và có 3 cạnh là AB, AC, BC C E G Tam giác DEG có 3 góc là góc A, góc E, góc G và có 3 cạnh là DE, DG, EG K N Tam giác MKN có 3 góc là góc M, góc K, góc N và có 3 cạnh là MK, MN, KN

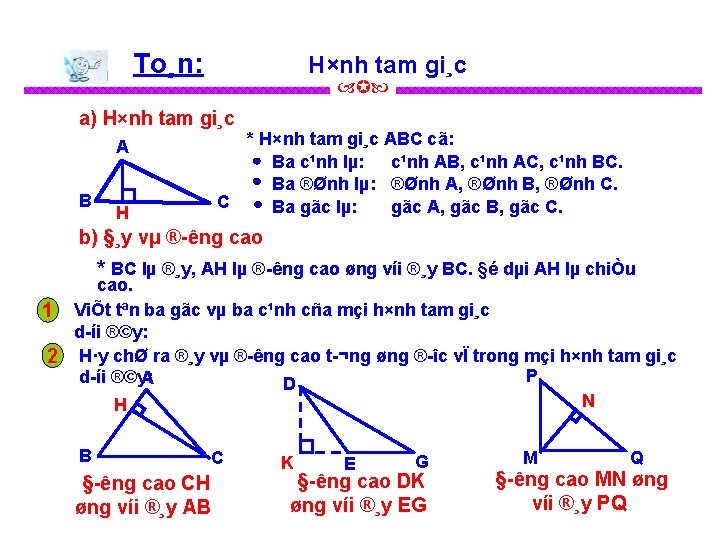
To¸n: H×nh tam gi¸c a) H×nh tam gi¸c * H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc A, gãc B, gãc C. A B H b) §¸y vµ ® êng cao * BC lµ ®¸y, AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu cao. 1 ViÕt tªn ba gãc vµ ba c¹nh cña mçi h×nh tam gi¸c d íi ®©y: 2 H·y chØ ra ®¸y vµ ® êng cao t ¬ng øng ® îc vÏ trong mçi h×nh tam gi¸c P d íi ®©y: A D N H B C § êng cao CH øng víi ®¸y AB K E G § êng cao DK øng víi ®¸y EG M Q § êng cao MN øng víi ®¸y PQ

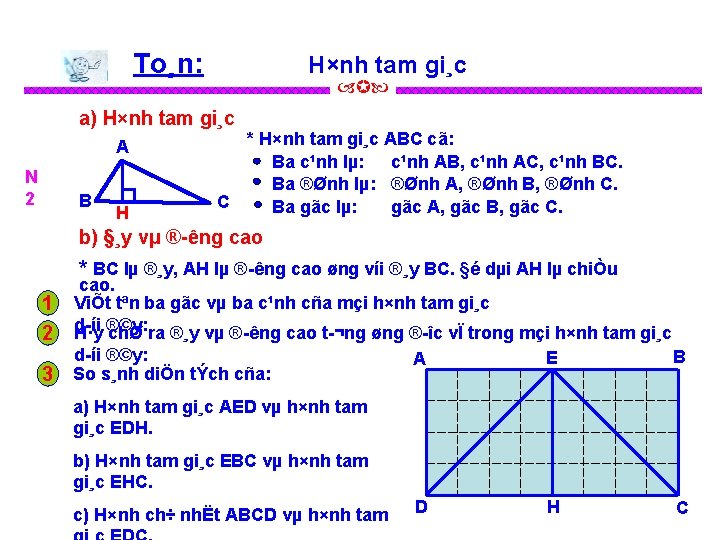
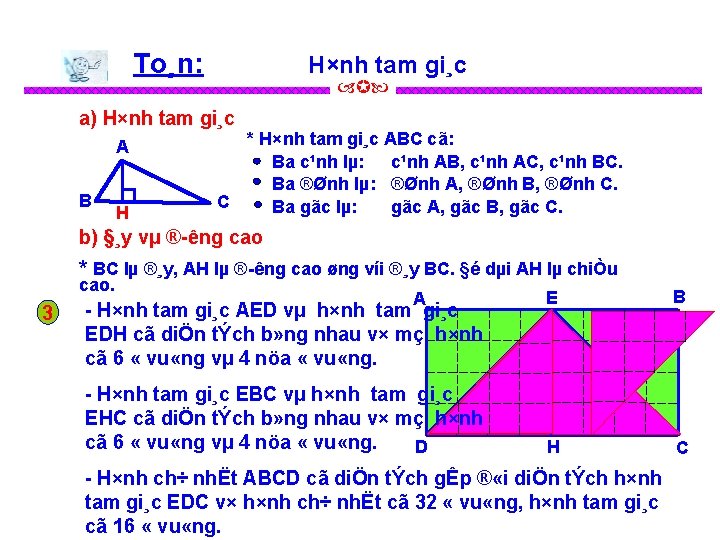
To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A N 2 B H * H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc A, gãc B, gãc C. b) §¸y vµ ® êng cao * BC lµ ®¸y, AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu 1 2 3 cao. ViÕt tªn ba gãc vµ ba c¹nh cña mçi h×nh tam gi¸c d íi ®©y: H·y chØ ra ®¸y vµ ® êng cao t ¬ng øng ® îc vÏ trong mçi h×nh tam gi¸c d íi ®©y: So s¸nh diÖn tÝch cña: A E B D H C a) H×nh tam gi¸c AED vµ h×nh tam gi¸c EDH. b) H×nh tam gi¸c EBC vµ h×nh tam gi¸c EHC. c) H×nh ch÷ nhËt ABCD vµ h×nh tam

To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A B H * H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc A, gãc B, gãc C. b) §¸y vµ ® êng cao * BC lµ ®¸y, AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu 1 2 3 cao. ViÕt tªn ba gãc vµ ba c¹nh cña mçi h×nh tam gi¸c d íi ®©y: H·y chØ ra ®¸y vµ ® êng cao t ¬ng øng ® îc vÏ trong mçi h×nh tam gi¸c d íi ®©y: A E B D H C

To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A B H * H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc A, gãc B, gãc C. b) §¸y vµ ® êng cao * BC lµ ®¸y, AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu 1 2 3 cao. ViÕt tªn ba gãc vµ ba c¹nh cña mçi h×nh tam gi¸c d íi ®©y: H·y chØ ra ®¸y vµ ® êng cao t ¬ng øng ® îc vÏ trong mçi h×nh tam gi¸c d íi ®©y: A E B D H C

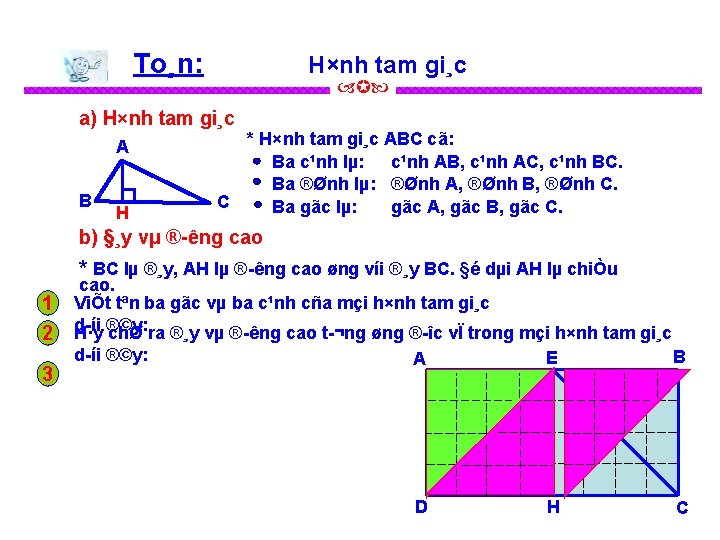
To¸n: H×nh tam gi¸c a) H×nh tam gi¸c A B H * H×nh tam gi¸c ABC cã: Ba c¹nh lµ: c¹nh AB, c¹nh AC, c¹nh BC. Ba ®Ønh lµ: ®Ønh A, ®Ønh B, ®Ønh C. C Ba gãc lµ: gãc A, gãc B, gãc C. b) §¸y vµ ® êng cao * BC lµ ®¸y, AH lµ ® êng cao øng víi ®¸y BC. §é dµi AH lµ chiÒu cao. 3 A H×nh tam gi¸c AED vµ h×nh tam gi¸c EDH cã diÖn tÝch b» ng nhau v× mçi h×nh cã 6 « vu «ng vµ 4 nöa « vu «ng. H×nh tam gi¸c EBC vµ h×nh tam gi¸c EHC cã diÖn tÝch b» ng nhau v× mçi h×nh cã 6 « vu «ng vµ 4 nöa « vu «ng. D E B H C H×nh ch÷ nhËt ABCD cã diÖn tÝch gÊp ® «i diÖn tÝch h×nh tam gi¸c EDC v× h×nh ch÷ nhËt cã 32 « vu «ng, h×nh tam gi¸c cã 16 « vu «ng.

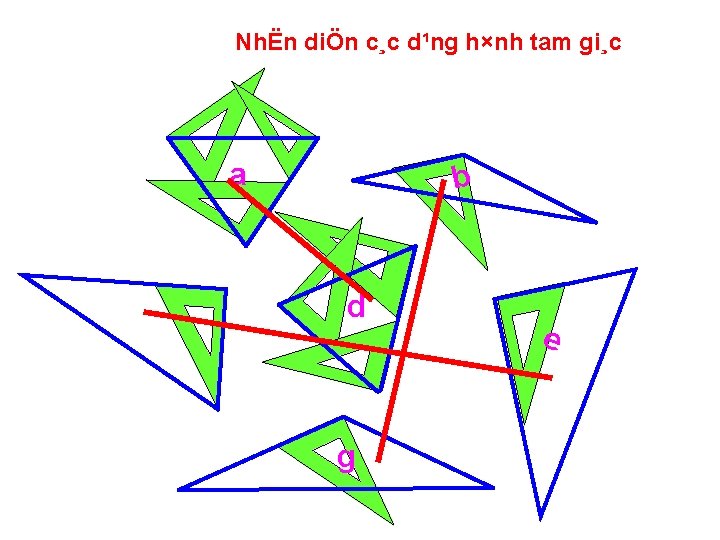
NhËn diÖn c¸c d¹ng h×nh tam gi¸c a c b d g e