2 Bi ton Cho hai tam gic ABC



2) Bài toán: Cho hai tam giác ABC và A’B’C’ có: Đặt trên tia AB đoạn thẳng AM = A’B’. A 1 B AMN N ABC ( 1 ) Ta có: C B’ C’ M 1= B ( đồng vị ) M 1= B’ B = B’ ( gt ) và có: A = A’ GT B = B’ Xét AMN và A’B’C’ có A = A’ ( gt ) AM = A’B’ ( cách dựng ) S KL S Qua M kẻ MN//BC ( N AC ) A’ M B = B’ (hình vẽ) S CM: A = A’ 2) Chứng minh AMN => ABC A’B’C’ = Từ (1) và (2) ( g. c. g )( 2) S ABC S || 1) Dựng AMN S Hai bước chứng minh:

1. Định lí Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau A B 2. Áp dụng C B’ C’ KL S và có: A = A’ GT B = B’ A’
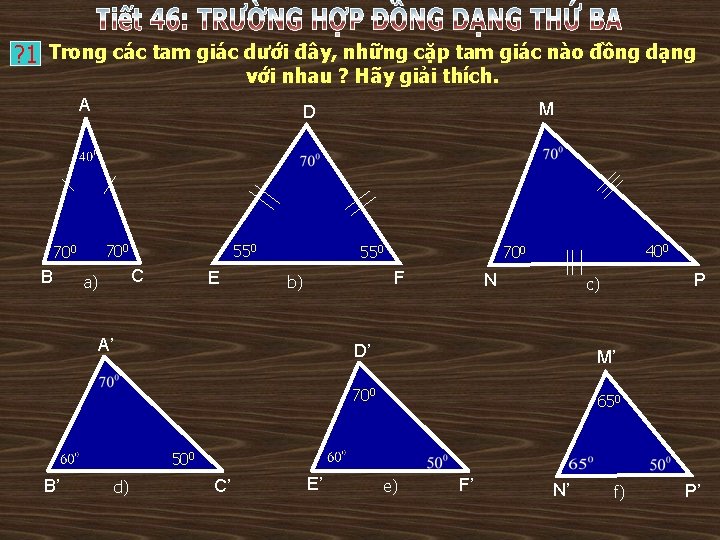
? 1 Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích. A 550 700 B M D C a) E 550 F b) A’ 400 700 N P c) D’ M’ 700 650 500 B’ d) C’ E’ e) F’ N’ f) P’
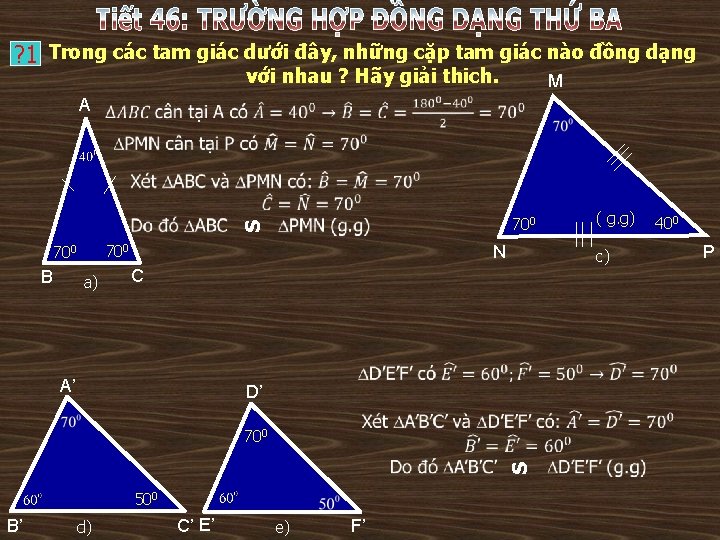
? 1 Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thich. M A S 700 700 B a) N c) C A’ D’ S 700 500 B’ d) C’ E’ e) F’ ( g. g) 400 P

? 2 a). Trong hình vẽ có bao nhiêu tam giác? Có cặp tam giác nào đồng dạng với nhau không? b). Hãy tính các độ dài x và y ( AD = x ; DC = y ) A x Giải 3 a) Trong hình vẽ có ba tam giác đó là: * ABC; ADB; BDC b) Ta có ABC S B 1 = C (gt) ABC ADB S Có: A chung ADB ( g. g ) ( c/m trên ) hay ( cm ) y 1 B * Xét ABC và ADB D 4, 5 C
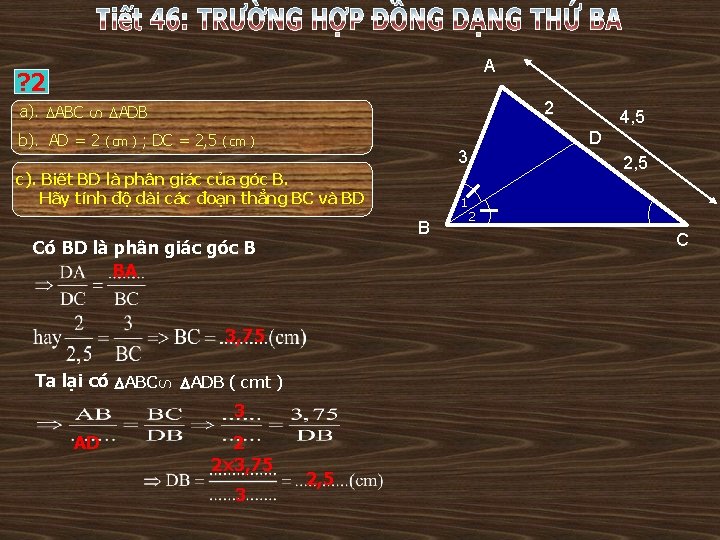
A a). ABC S ? 2 b). AD = 2 2 ADB ( cm ) ; DC = 2, 5 ( cm ) 3, 75 S ADB ( cmt ) 3 AD 2 2 x 3, 75 3 1 B Có BD là phân giác góc B BA Ta lại có ABC D 3 c). Biết BD là phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD 2, 5 4, 5 2 C
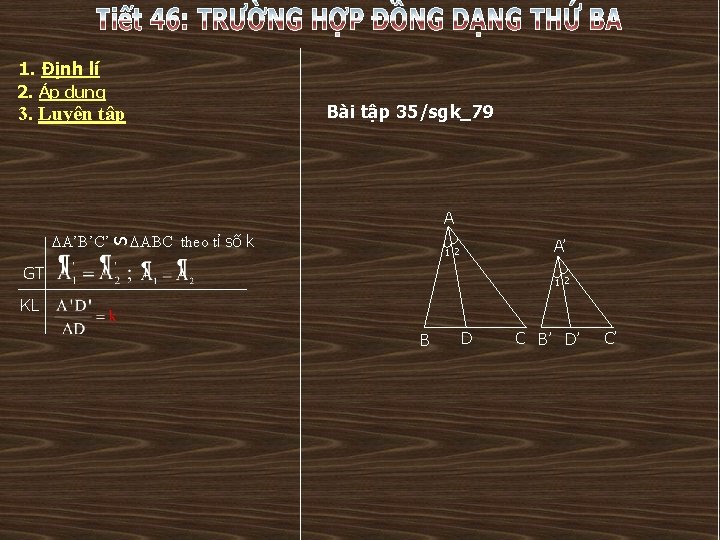
1. Định lí 2. Áp dụng Bài tập 35/sgk_79 3. Luyện tập A ABC theo tỉ số k S A’B’C’ A’ 1 2 GT 1 2 KL B D C B’ D’ C’

1. Định lí 2. Áp dụng Bài tập 35/sgk_79 Chứng minh: S A’B’C’ ABC theo tỉ số k A’B’C’ S 3. Luyện tập ABC theo tỉ số k, vậy nên ta có: GT và KL A 1 2 ( cmt ) B D C B’ D’ A’B’D’ S Xét A’B’D’ và ABD có: A’ 1 2 ABD ( g. g ) C’ Khi hai tam giác đồng dạng với nhau thì tỉ số hai đường phân giác tương ứng và tỉ số đồng dạng của chúng như thế nào ?
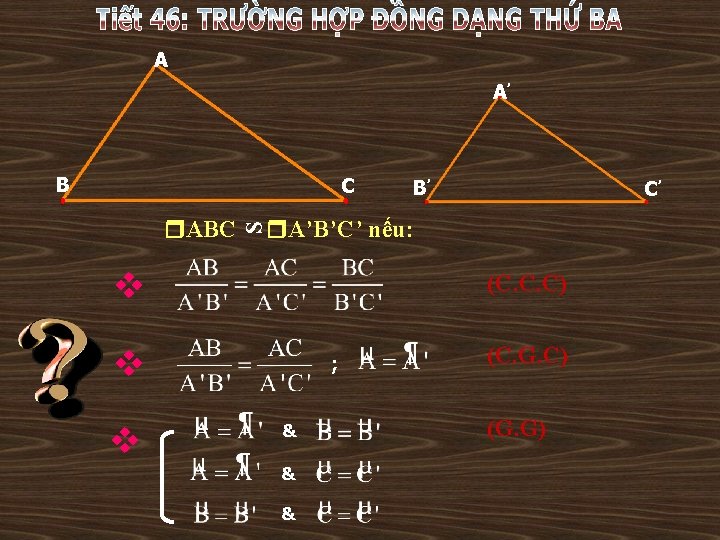

1. Định lí A Học thuộc, nắm vững các định lí về ba trường hợp đồng dạng của hai tam giác. A’ So sánh với ba trường hợp bằng nhau của hai tam giác. B C B’ KL S và có: A = A’ GT B = B’ 2. Áp dụng C’ Bài tập về nhà: Bài 36; 37; 38 ( SGK ) Bài 39; 40; 41 ( SBT )

- Slides: 13