Cho tam gic ABC vung ti A c

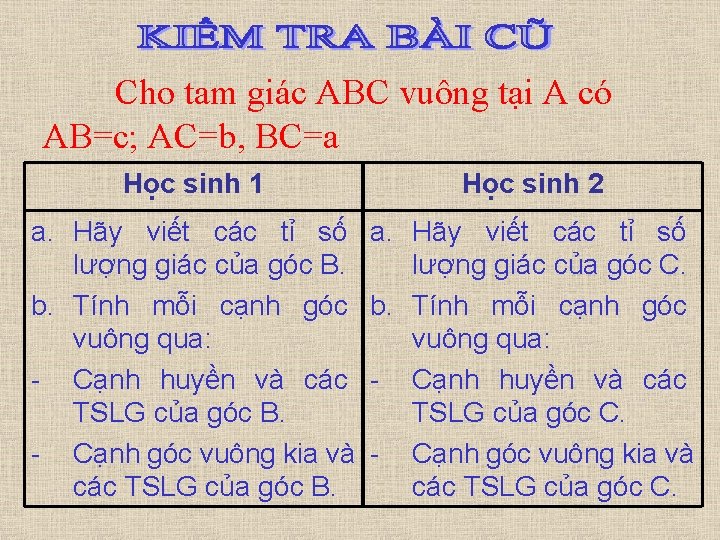
Cho tam giác ABC vuông tại A có AB=c; AC=b, BC=a Học sinh 1 Học sinh 2 a. Hãy viết các tỉ số lượng giác của góc B. b. Tính mỗi cạnh góc vuông qua: - Cạnh huyền và các TSLG của góc B. - Cạnh góc vuông kia và các TSLG của góc B. a. Hãy viết các tỉ số lượng giác của góc C. b. Tính mỗi cạnh góc vuông qua: - Cạnh huyền và các TSLG của góc C. - Cạnh góc vuông kia và các TSLG của góc C.
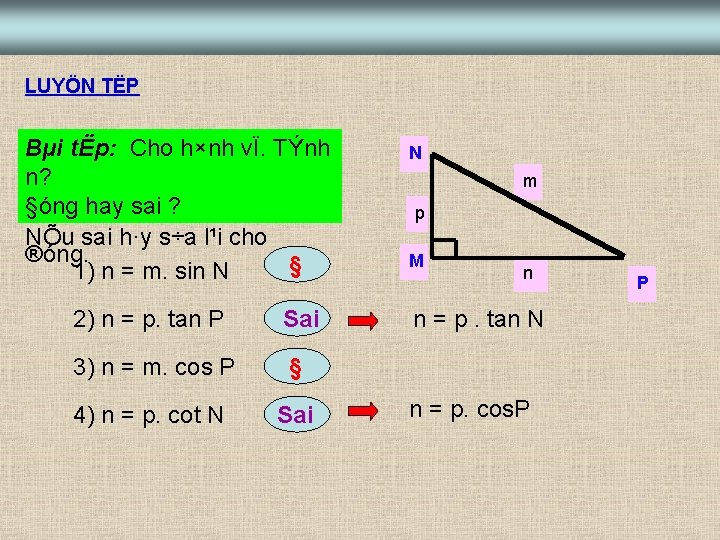
LUYÖN TËP Bµi tËp: Cho h×nh vÏ. TÝnh n? §óng hay sai ? NÕu sai h·y s÷a l¹i cho ®óng. § 1) n = m. sin N 2) n = p. tan P Sai 3) n = m. cos P § 4) n = p. cot N Sai N m p M n n = p. tan N n = p. cos. P P
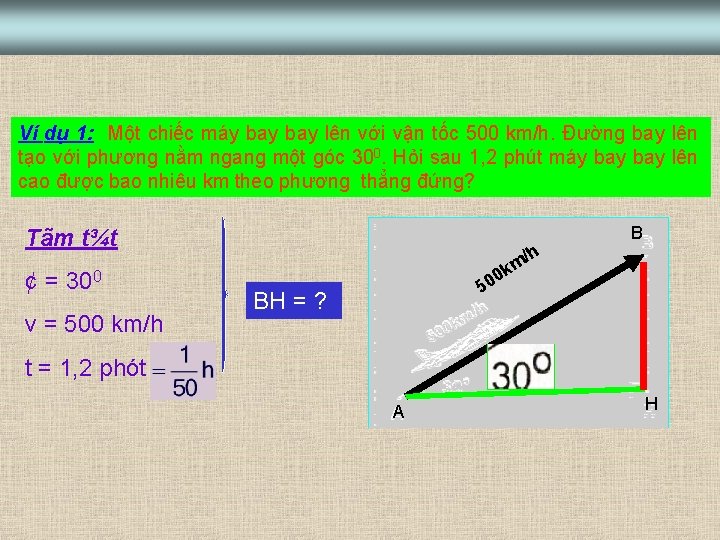
Ví dụ 1: Một chiếc máy bay lên với vận tốc 500 km/h. Đường bay lên tạo với phương nằm ngang một góc 300. Hỏi sau 1, 2 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng? B Tãm t¾t ¢ = 300 v = 500 km/h h / m k 0 50 BH = ? t = 1, 2 phót A H


Ví dụ 3: Cho tam giác ABC vuông tại A, biết AB= 4, AC=6. Tính các cạnh và các góc còn lại của tam giác vuông.

gt AB=4; AC=6. BC= ? kl C Tam giác ABC (góc A= 900) 6 góc B=? góc C=? A 4 B Áp dụng định lý pitago vào tam giác vuông ABC ta có: Ta có: Tam giác ABC có
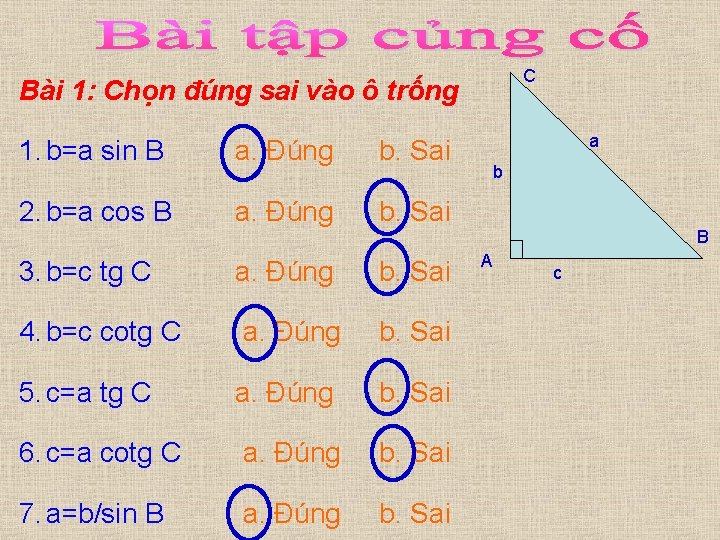
C Bài 1: Chọn đúng sai vào ô trống 1. b=a sin B a. Đúng b. Sai 2. b=a cos B a. Đúng b. Sai a b B 3. b=c tg C a. Đúng b. Sai 4. b=c cotg C a. Đúng b. Sai 5. c=a tg C a. Đúng b. Sai 6. c=a cotg C a. Đúng b. Sai 7. a=b/sin B a. Đúng b. Sai A c


H íngdÉn häc ë nhµ Häc thuéc néi dung ®Þnh lÝ vµ n¾m ch¾c c¸c hÖ thøc trªn Xem l¹i ph ¬ng ph¸p gi¶i c¸c vÝ dô vµ bµi tËp ®· gi¶i, t×m thªm c¸ch gi¶i kh¸c (nÕu cã) C¸c b¹n kh¸, giái lµm thªm bµi 57, 58(SBT) H «m sau c¸c em häc tiÕp bµi 4, môc 2 VËn dông ®Ó lµm c¸c bµi tËp 27, 29(SGK) 53, 54, 56(SBT)

CAÙM ÔN THAÀY CO VAØ CAÙC EM HOÏC SINH ÑAÕ THAM DÖÏ TIEÁT HOÏC
- Slides: 11