Kim tra bi c Cho tam gic ABC

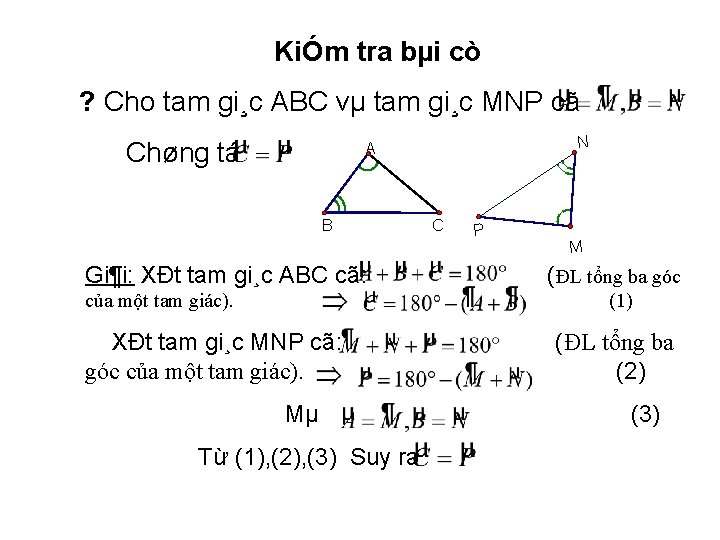
KiÓm tra bµi cò ? Cho tam gi¸c ABC vµ tam gi¸c MNP cã Chøng tá N A B Gi¶i: XÐt tam gi¸c ABC cã: của một tam giác). C P M ( ĐL tổng ba góc (1) XÐt tam gi¸c MNP cã: góc của một tam giác). Mµ Từ (1), (2), (3) Suy ra (ĐL tổng ba (2) (3)
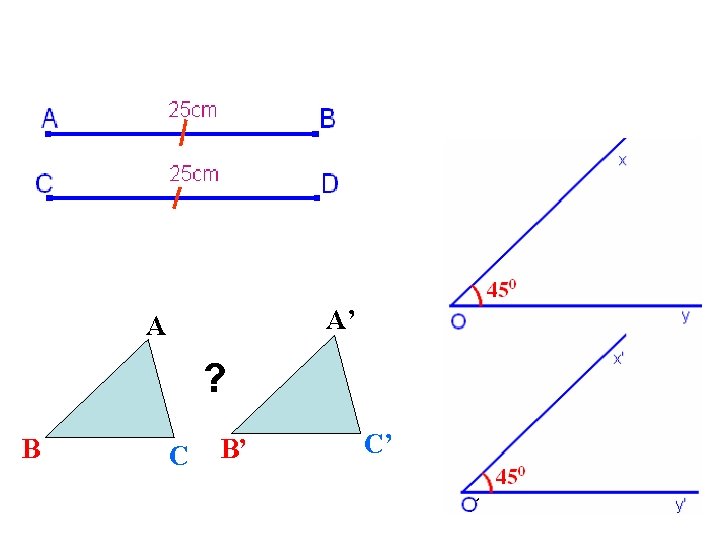
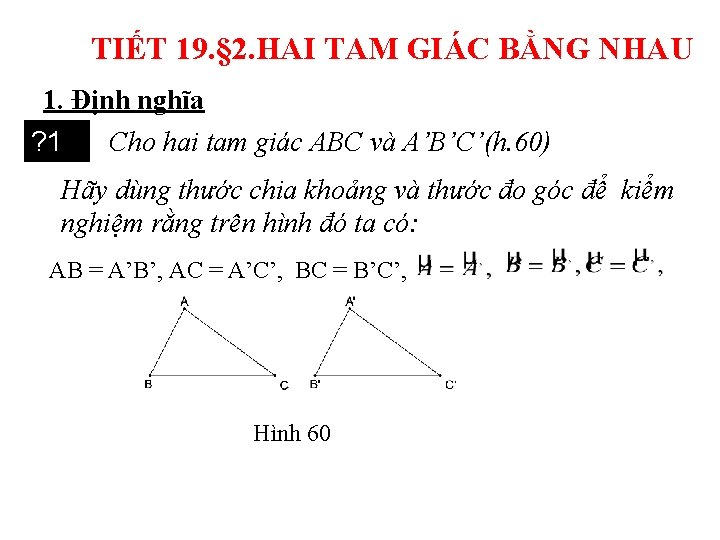
TIẾT 19. § 2. HAI TAM GIÁC BẰNG NHAU 1. Định nghĩa Cho hai tam giác ABC và A’B’C’(h. 60) ? 1 Hãy dùng thước chia khoảng và thước đo góc để kiểm nghiệm rằng trên hình đó ta có: AB = A’B’, AC = A’C’, BC = B’C’, Hình 60
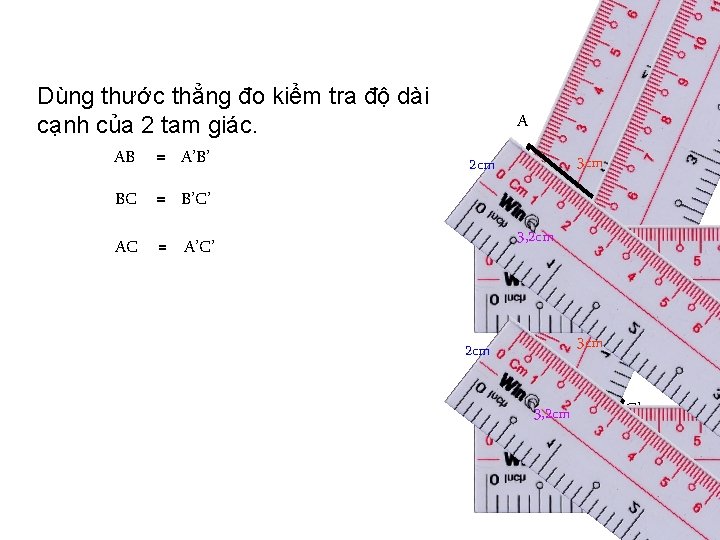
Dùng thước thẳng đo kiểm tra độ dài cạnh của 2 tam giác. AB = A’B’ BC = B’C’ AC = A’C’ A 3 cm 2 cm B C 3, 2 cm A’ 3 cm 2 cm B’ 3, 2 cm C’
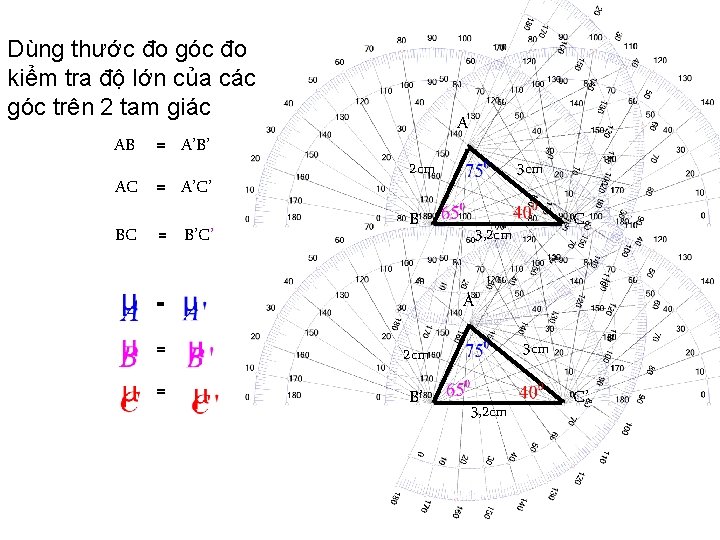
Dùng thước đo góc đo kiểm tra độ lớn của các góc trên 2 tam giác AB = A’B’ AC = A’C’ BC = B’C’ A 2 cm B 3 cm C 3, 2 cm A’ = = 2 cm = B’ 3 cm 3, 2 cm C’

TIẾT 19. § 2. HAI TAM GIÁC BẰNG NHAU 1. Định nghĩa A A’ ? 1 ABC và A’B’C’ có: B AB = A’B’, AC = A’C’, BC = B’C’, C B’ Hai tam giác ABC và A’B’C’ được gọi là hai tam giác bằng nhau. Hai *Haiđỉnh. AAvàvàA’ A’gọi (Blàvàhai B’, đỉnh C vàtương C’) gọi ứng. . là hai Tìmđỉnh 2 đỉnh tương ứng khác? *Hai Haigóc góc. AAvà vàA’ A’gọi (B là vàhai B’, góc C vàtương C’) gọi ứng. là Tìm hai góc 2 góc tương ứng khác? Hai cạnh AB và A’B’ gọi là hai cạnh tương ứng. Tìm 2 cạnh tương ứng khác? *Hai cạnh AB và A’B’ (BC và B’C’, AC và A’ C’) gọi là hai cạnh tương ứng. Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau. C’

TIẾT 19. § 2. HAI TAM GIÁC BẰNG NHAU 1. Định nghĩa 2. Kí hiệu Hai tam giác ABC và tam giác A’B’C’ bằng nhau , ta viết: ***Qui ước: Khi viết hai tam giác bằng nhau ta viết tên các đỉnh tương ứng theo cùng một thứ tự

? 2 N A Giải: a)XÐt tam gi¸c ABC cã: (®Þnh P B C M a) Hai tam giác ABC và MNP có bằng nhau hay không? ( các cạnh hoặc các góc bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Nếu có hãy viết kí hiệu về sự bằng nhau của hai tam giác đó. b) Hãy tìm : Đỉnh tương ứng với đỉnh A, góc tương ứng với góc N, cạnh tương ứng với cạnh AC? c) Điền vào chỗ trống (. . . ): ACB = B =. . . …. , AC =. . . , lÝ…) (1) XÐt tam gi¸c MNP cã: (®Þnh lÝ …) (2) Mµ (3 Vậy: Từ (1), (2), (3) Suy ra b) Đỉnh M tương ứng với đỉnh A Góc B tương ứng với góc N Cạnh MP tương ứng với cạnh AC
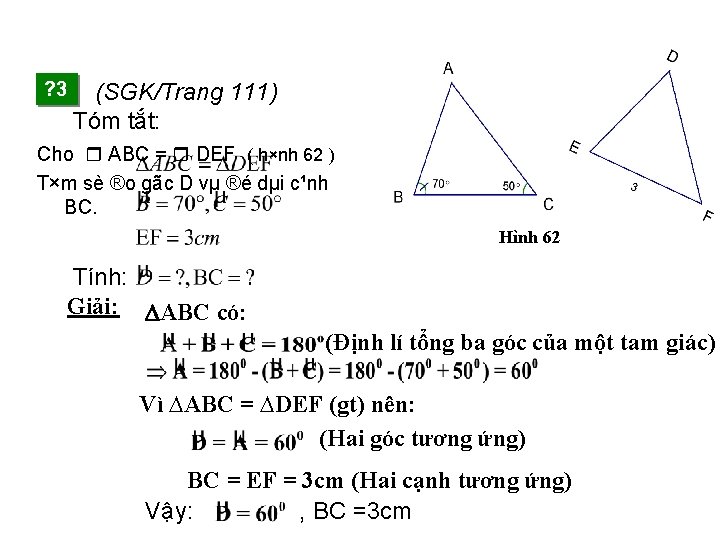
? 3 (SGK/Trang 111) Tóm tắt: Cho ABC = DEF ( h×nh 62 ) T×m sè ®o gãc D vµ ®é dµi c¹nh BC. Hình 62 Tính: Giải: ABC có: (Định lí tổng ba góc của một tam giác) Vì ∆ABC = ∆DEF (gt) nên: (Hai góc tương ứng) BC = EF = 3 cm (Hai cạnh tương ứng) Vậy: , BC =3 cm
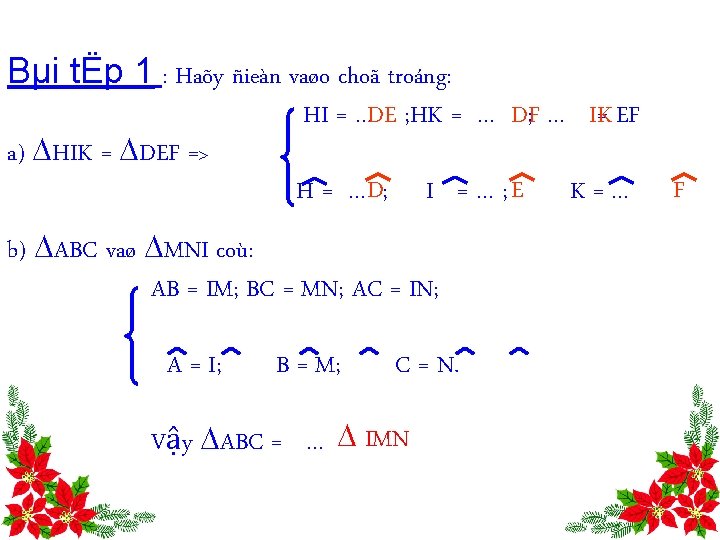
Bµi tËp 1 : Haõy ñieàn vaøo choã troáng: a) HIK = DEF => HI = …DE ; HK = … DF; … IK= EF H = …D; I = … ; E b) ABC vaø MNI coù: AB = IM; BC = MN; AC = IN; A = I; B = M; C = N. Vậy ABC = … IMN K=… F
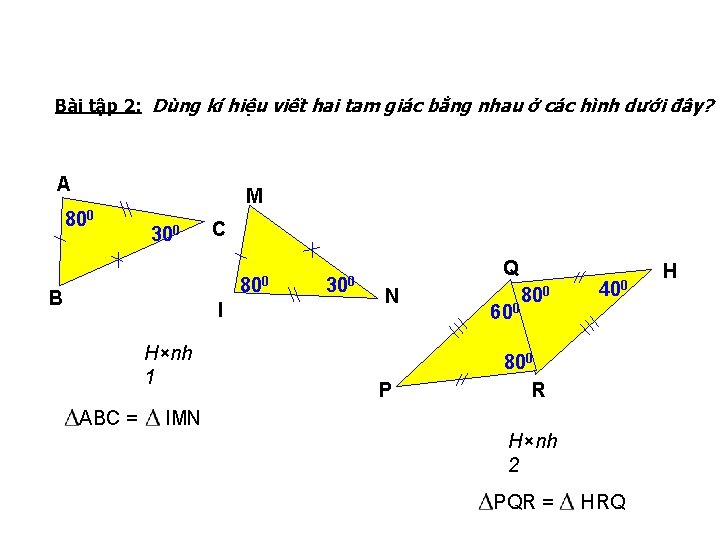
Bài tập 2: Dùng kí hiệu viết hai tam giác bằng nhau ở các hình dưới đây? A M 800 300 C 800 B I H×nh 1 ABC = 300 Q N P 600 800 400 800 R IMN H×nh 2 PQR = HRQ H

H íng dÉn vÒ nhµ Häc thuéc ®Þnh nghÜa: Hai tam gi¸c b» ng nhau, kÝ hiÖu hai tam gi¸c b» ng nhau. BT 11, 12, 13, 14 SGK Đọc trước bài “Trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh(c. c. c)
- Slides: 13