ASLevel Maths Mechanics 2 for Edexcel M 2

AS-Level Maths: Mechanics 2 for Edexcel M 2. 3 Centres of Mass These icons indicate that teacher’s notes or useful web addresses are available in the Notes Page. This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 36 © Boardworks Ltd 2006

Centres of mass Contents Centres of mass Two dimensions Equilibrium Examination-style questions 2 of 36 © Boardworks Ltd 2006

Centres of mass The centre of mass of a body is the point at which the weight acts. This point can be located for one, two and three dimensional objects and composite bodies. Sometimes the centre of mass of a uniform body can be found by symmetry. In general, we use moments to determine the position of the centre of mass. The positions of the centres of mass of certain bodies are given as formulae, which can be applied without working. 3 of 36 © Boardworks Ltd 2006

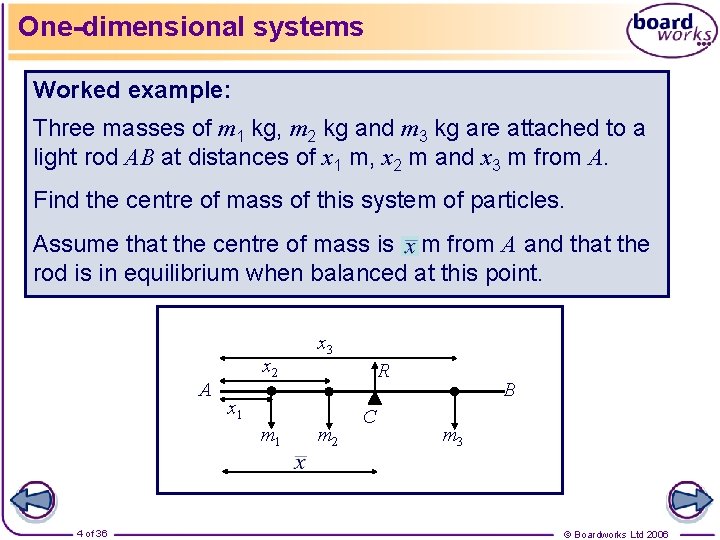
One-dimensional systems Worked example: Three masses of m 1 kg, m 2 kg and m 3 kg are attached to a light rod AB at distances of x 1 m, x 2 m and x 3 m from A. Find the centre of mass of this system of particles. Assume that the centre of mass is m from A and that the rod is in equilibrium when balanced at this point. A x 2 R x 1 m 1 4 of 36 x 3 m 2 C B m 3 © Boardworks Ltd 2006

One-dimensional systems The forces can be resolved vertically: R = m 1 g + m 2 g + m 3 g Taking moments about A: m 1 gx 1 + m 2 gx 2 + m 3 gx 3 = R m 1 gx 1 + m 2 gx 2 + m 3 gx 3 = (m 1 g + m 2 g + m 3 g) Therefore, 5 of 36 © Boardworks Ltd 2006

The weighted mean The previous result can be extended to the general case. is called the weighted mean and enables us to calculate the position of the centre of mass for a 1 -D system. The formula for the weighted mean is usually written: 6 of 36 © Boardworks Ltd 2006

One-dimensional systems Example: Four particles of mass 1 kg, 2. 5 kg and 3 kg are attached to a light, rigid, horizontal rod AB of length 2 m. The particles are attached to the rod as shown in the diagram. Find the distance of the system’s centre of mass from A. A 0. 4 1 g 3 g 0. 6 1 2. 5 g B 2 g Find the weighted mean: Therefore the centre of mass of the system is 0. 906 m (3 s. f. ) from A. 7 of 36 © Boardworks Ltd 2006

One-dimensional systems A three-sectioned telescopic aerial is extended horizontally. The first section is 20 cm in length and has a mass of 100 g, the second section is 15 cm in length and has a mass of 70 g and the third section is 10 cm in length with a mass of 40 g. By modelling each section of the aerial as a uniform rod, find the centre of mass of this system. 8 of 36 © Boardworks Ltd 2006

One-dimensional systems Since each section of aerial is modelled as a uniform rod, the weight is taken to act at the centre of each section. A 10 10 0. 1 g 7. 5 0. 07 g 5 5 B 0. 04 g Using the weighted mean: Therefore the centre of mass of the aerial is 21. 5 cm (3 s. f) from A. 9 of 36 © Boardworks Ltd 2006

Two dimensions Contents Centres of mass Two dimensions Equilibrium Examination-style questions 10 of 36 © Boardworks Ltd 2006

Two dimensions A composite body can be made up of a series of rods or a series of laminas. Sometimes the particles of a system are not in a straight line. In these cases we can find the centre of mass in terms of x - and y-coordinates relative to some fixed axes. The weighted mean is extended to 2 -dimensions to give the coordinates of the centre of mass. 11 of 36 © Boardworks Ltd 2006

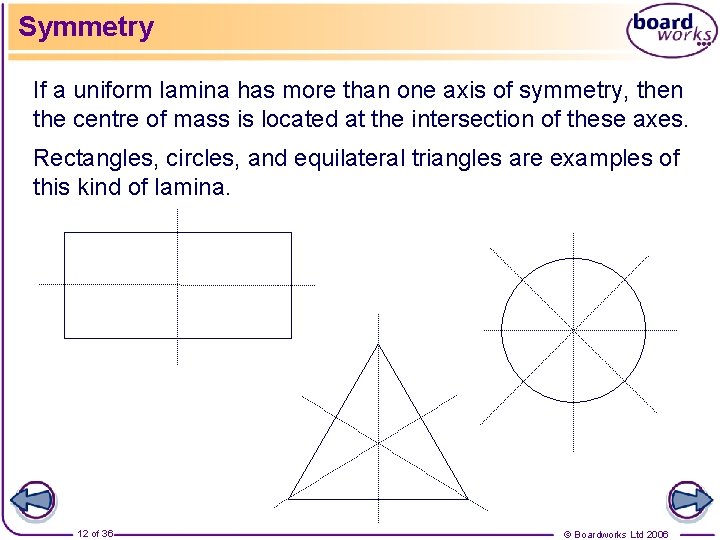
Symmetry If a uniform lamina has more than one axis of symmetry, then the centre of mass is located at the intersection of these axes. Rectangles, circles, and equilateral triangles are examples of this kind of lamina. 12 of 36 © Boardworks Ltd 2006

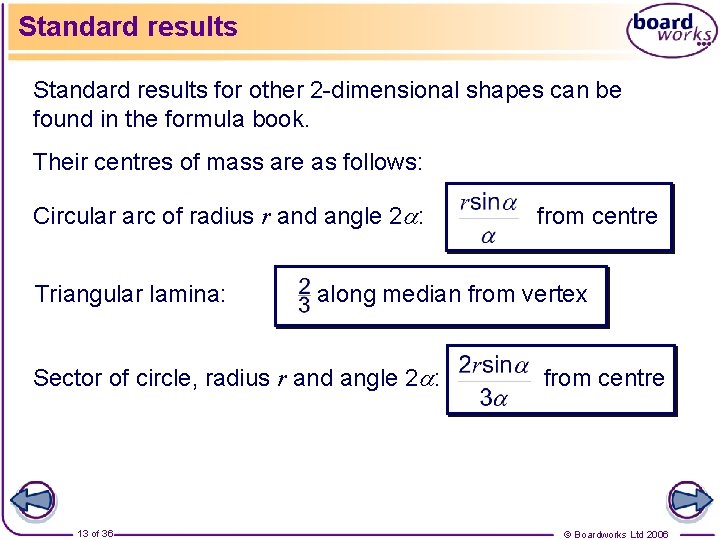
Standard results for other 2 -dimensional shapes can be found in the formula book. Their centres of mass are as follows: Circular arc of radius r and angle 2 : Triangular lamina: along median from vertex Sector of circle, radius r and angle 2 : 13 of 36 from centre © Boardworks Ltd 2006

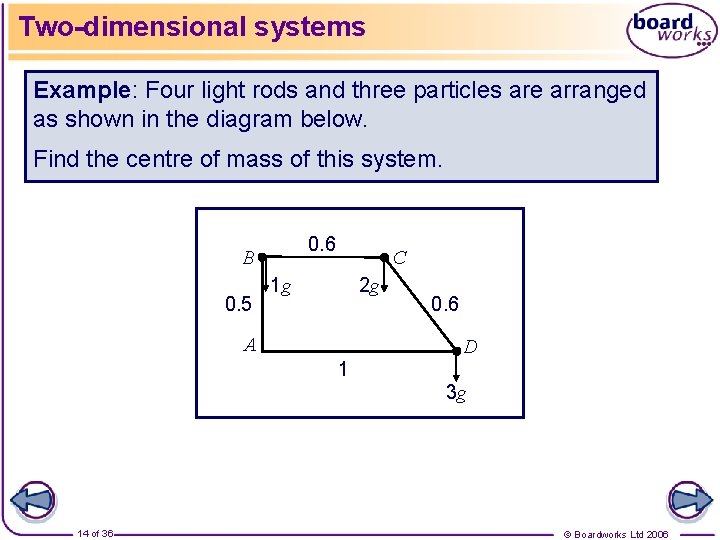
Two-dimensional systems Example: Four light rods and three particles are arranged as shown in the diagram below. Find the centre of mass of this system. 0. 6 B 0. 5 C 1 g 2 g A 0. 6 D 1 3 g 14 of 36 © Boardworks Ltd 2006

Two-dimensional systems When working in 2 -D, it is often helpful to tabulate the information needed before calculating the weighted means. The point A is taken to be the origin. The x-coordinates represent the horizontal distance from A, while the y -coordinates represent the vertical distance from A. mass 1 2 3 x 0 0. 6 1 y 0. 5 0 Therefore the centre of mass of the system is 0. 7 m from AB and 0. 25 m from AD. 15 of 36 © Boardworks Ltd 2006

Two-dimensional systems Example: A uniform lamina is in the shape of the letter ‘L’, with dimensions as shown in the diagram. Find the centre of mass of this lamina. 0. 2 1 0. 2 0. 5 16 of 36 © Boardworks Ltd 2006

Two-dimensional systems The lamina should be split into two rectangles enabling each centre of mass to be found by symmetry. Since the lamina is uniform the mass of each rectangle mass 0. 2 0. 06 will be proportional x 0. 1 0. 35 to its area. y 0. 5 0. 1 C 1 0. 2 0. 8 0. 3 0. 2 A 0. 5 B Therefore the centre of mass of the ‘L’ shape lamina is 0. 158 m (3 s. f. ) from AC and 0. 408 m (3 s. f. ) from AB. 17 of 36 © Boardworks Ltd 2006

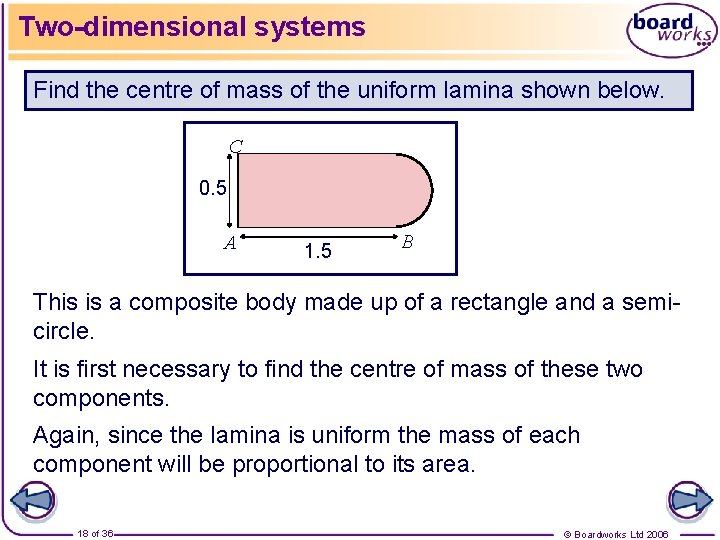
Two-dimensional systems Find the centre of mass of the uniform lamina shown below. C 0. 5 A 1. 5 B This is a composite body made up of a rectangle and a semicircle. It is first necessary to find the centre of mass of these two components. Again, since the lamina is uniform the mass of each component will be proportional to its area. 18 of 36 © Boardworks Ltd 2006

Two-dimensional systems The centre of mass of the rectangular component, by symmetry, is 0. 75 m from AC and 0. 25 m from AB. The centre of mass of the semi-circular component is found from the standard result for the centre of mass of a sector of a circle. For a sector of radius r and angle 2 : from the centre. Here, r = 0. 25 m and 2 = . The centre of mass = 19 of 36 © Boardworks Ltd 2006

Two-dimensional systems Area of rectangle = 0. 5 × 1. 5 = 0. 75 Area of semi-circle = ½ × × 0. 252 = 0. 03125 mass 0. 75 x 0. 75 y 0. 25 0. 03125 1. 5 + 0. 25 = 0. 849 (3 s. f. ) = 0. 25 Therefore the centre of mass of the lamina is 0. 849 m (3 s. f. ) from AC and 0. 25 m from AB. 20 of 36 © Boardworks Ltd 2006

Equilibrium Contents Centres of mass Two dimensions Equilibrium Examination-style questions 21 of 36 © Boardworks Ltd 2006

Equilibrium A lamina suspended from a point is in equilibrium if its centre of mass is directly below the point from which it is suspended. 22 of 36 © Boardworks Ltd 2006

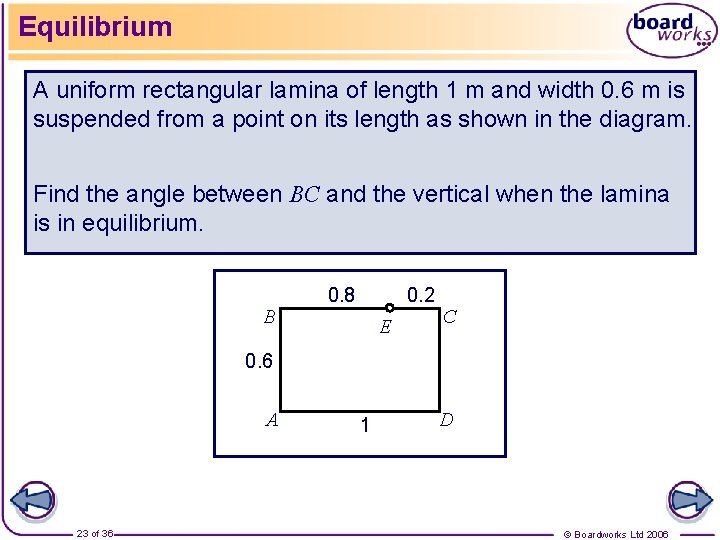
Equilibrium A uniform rectangular lamina of length 1 m and width 0. 6 m is suspended from a point on its length as shown in the diagram. Find the angle between BC and the vertical when the lamina is in equilibrium. B 0. 8 0. 2 E C 0. 6 A 23 of 36 1 D © Boardworks Ltd 2006

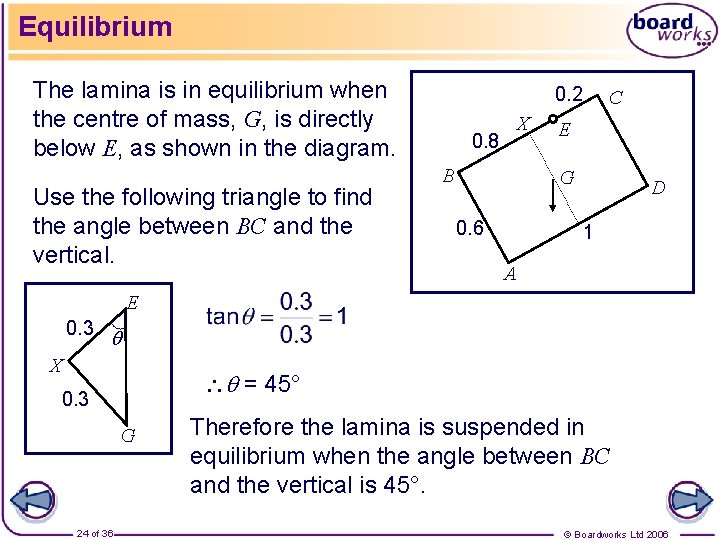
Equilibrium The lamina is in equilibrium when the centre of mass, G, is directly below E, as shown in the diagram. Use the following triangle to find the angle between BC and the vertical. 0. 2 0. 8 X B C E G 0. 6 D 1 A E 0. 3 X = 45° 0. 3 G 24 of 36 Therefore the lamina is suspended in equilibrium when the angle between BC and the vertical is 45°. © Boardworks Ltd 2006

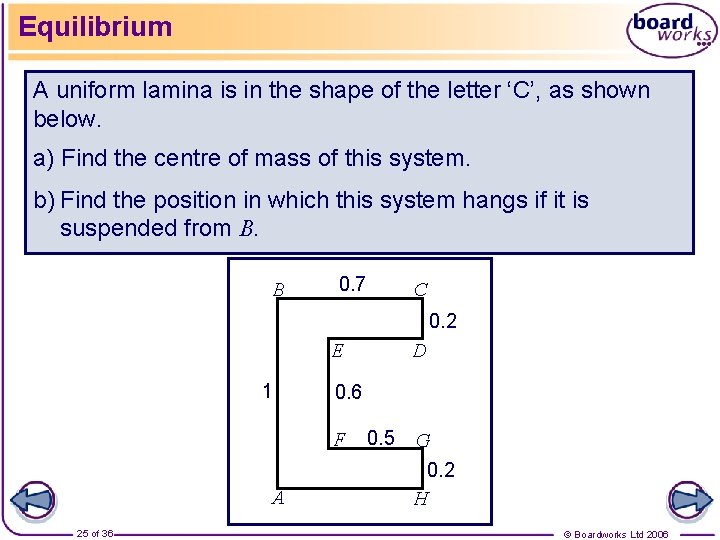
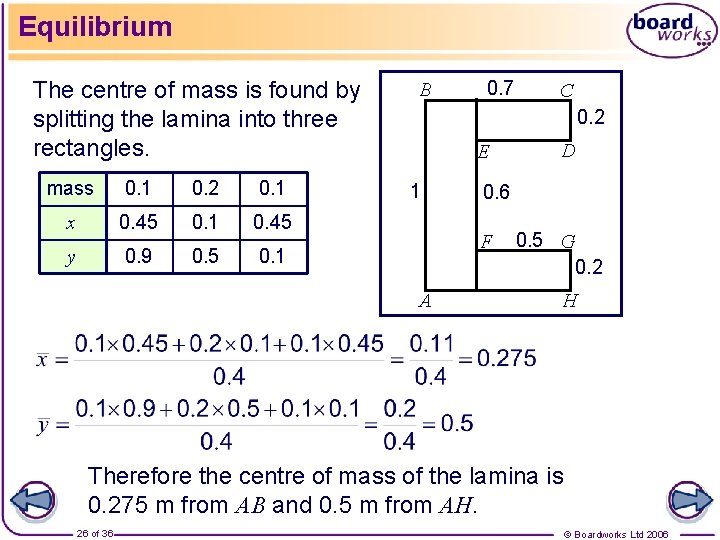
Equilibrium A uniform lamina is in the shape of the letter ‘C’, as shown below. a) Find the centre of mass of this system. b) Find the position in which this system hangs if it is suspended from B. B 0. 7 C 0. 2 D E 1 0. 6 F A 25 of 36 0. 5 G 0. 2 H © Boardworks Ltd 2006

Equilibrium The centre of mass is found by splitting the lamina into three rectangles. mass 0. 1 0. 2 0. 1 x 0. 45 0. 1 0. 45 y 0. 9 0. 5 0. 1 B 0. 7 C 0. 2 E 1 0. 6 F A D 0. 5 G 0. 2 H Therefore the centre of mass of the lamina is 0. 275 m from AB and 0. 5 m from AH. 26 of 36 © Boardworks Ltd 2006

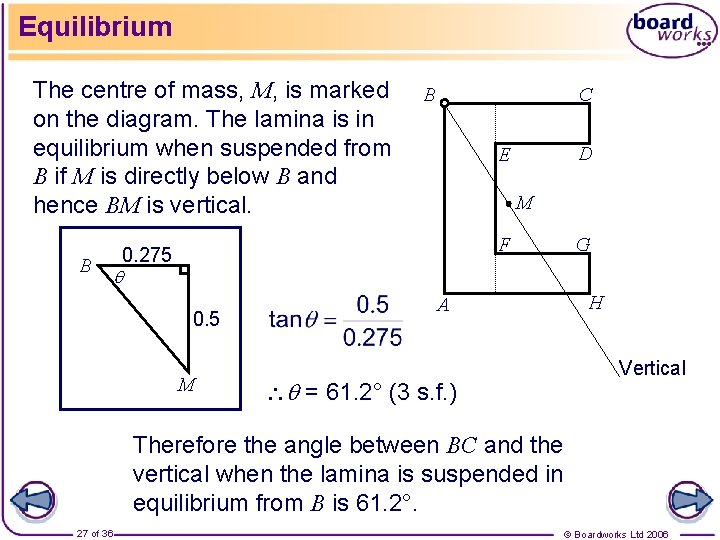
Equilibrium The centre of mass, M, is marked on the diagram. The lamina is in equilibrium when suspended from B if M is directly below B and hence BM is vertical. B B C D E M F 0. 275 0. 5 M A = 61. 2° (3 s. f. ) G H Vertical Therefore the angle between BC and the vertical when the lamina is suspended in equilibrium from B is 61. 2°. 27 of 36 © Boardworks Ltd 2006

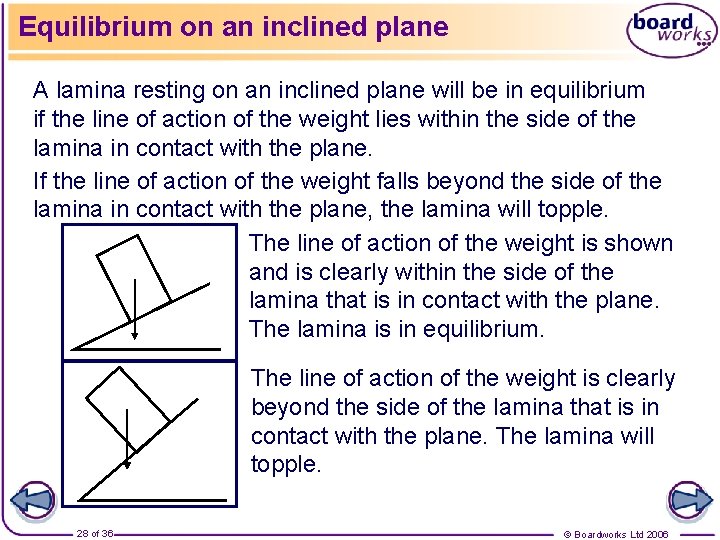
Equilibrium on an inclined plane A lamina resting on an inclined plane will be in equilibrium if the line of action of the weight lies within the side of the lamina in contact with the plane. If the line of action of the weight falls beyond the side of the lamina in contact with the plane, the lamina will topple. The line of action of the weight is shown and is clearly within the side of the lamina that is in contact with the plane. The lamina is in equilibrium. The line of action of the weight is clearly beyond the side of the lamina that is in contact with the plane. The lamina will topple. 28 of 36 © Boardworks Ltd 2006

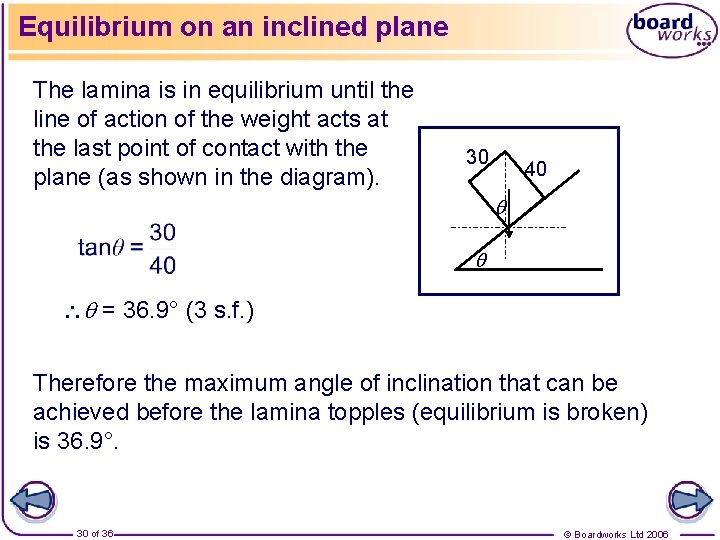
Equilibrium on an inclined plane A rectangular lamina ABCD has AB = 40 cm and AD = 30 cm. The lamina is resting on its shorter side on a plane inclined at an angle of ° to the horizontal. What is the maximum value of for which the lamina will remain in equilibrium? 29 of 36 © Boardworks Ltd 2006

Equilibrium on an inclined plane The lamina is in equilibrium until the line of action of the weight acts at the last point of contact with the plane (as shown in the diagram). 30 40 = 36. 9° (3 s. f. ) Therefore the maximum angle of inclination that can be achieved before the lamina topples (equilibrium is broken) is 36. 9°. 30 of 36 © Boardworks Ltd 2006

Examination-style questions Contents Centres of mass Two dimensions Equilibrium Examination-style questions 31 of 36 © Boardworks Ltd 2006

Exam question 1 A uniform plane lamina is in the shape of a square next to a rectangle. The length of a side of the square is x cm and the rectangle is cm by 2 x cm. Find the distance of the centre of mass of this lamina from A in terms of x. x A 32 of 36 x 2 x © Boardworks Ltd 2006

Exam question 1 Area of square = x 2 Area of rectangle = x 2 The centre of mass of both the square and the rectangle are found by symmetry. mass x x 2 2 x y 33 of 36 © Boardworks Ltd 2006

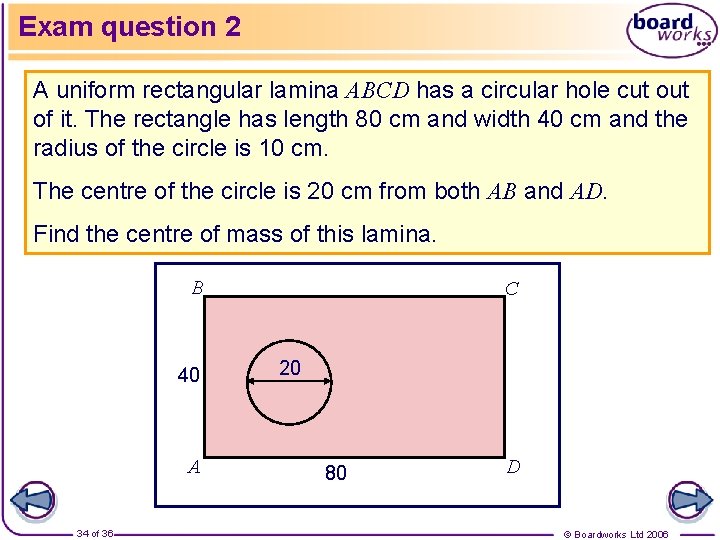
Exam question 2 A uniform rectangular lamina ABCD has a circular hole cut of it. The rectangle has length 80 cm and width 40 cm and the radius of the circle is 10 cm. The centre of the circle is 20 cm from both AB and AD. Find the centre of mass of this lamina. B 40 A 34 of 36 C 20 80 D © Boardworks Ltd 2006

Exam question 2 To find the centre of mass of this lamina consider the circle, the rectangle and the given lamina separately. Area of rectangle = 3200 cm 2 Area of circle = 100 cm 2 Area of lamina = 3200 – 100 cm 2 The centre of mass of the rectangle is 40 cm from AB and 20 cm from AD. The centre of mass of the circle is 20 cm from both AB and AD. 35 of 36 circle lamina rectangle mass 100 3200– 100 3200 x 20 40 y 20 20 © Boardworks Ltd 2006

Exam question 2 Forming an equation for : = 42. 177 (5 s. f. ) Forming an equation for : = 20 Therefore the centre of mass of the lamina is 42. 2 cm from AB and 20 cm from AD. 36 of 36 © Boardworks Ltd 2006