ASLevel Maths Core 1 for Edexcel C 1
































- Slides: 38

AS-Level Maths: Core 1 for Edexcel C 1. 1 Algebra and functions 1 This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 38 © Boardworks Ltd 2005

Using and manipulating surds Contents Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 2 of 38 © Boardworks Ltd 2005

Types of number We can classify numbers into the following sets: The set of natural numbers, : Positive whole numbers {0, 1, 2, 3, 4 …} The set of integers, : Positive and negative whole numbers {0, ± 1, ± 2, ± 3 …} The set of rational numbers, : Numbers that can be expressed in the form , where n and m are integers. All fractions and all terminating and recurring decimals are rational numbers; for example, ¾, – 0. 63, 0. 2. The set of real numbers, : All numbers including irrational numbers; that is, numbers that cannot be expressed in the form , where n and m are integers. For example, and. 3 of 38 © Boardworks Ltd 2005

Introducing surds When the square root of a number, for example √ 2, √ 3 or √ 5, is irrational, it is often preferable to write it with the root sign. Numbers written in this form are called surds. Can you explain why √ 1. 69 is not a surd? √ 1. 69 is not a surd because it is not irrational. This uses the fact that = 1. 3 4 of 38 © Boardworks Ltd 2005

Manipulating surds When working with surds it is important to remember the following two rules: and Also: You should also remember that, by definition, √a means the positive square root of a. 5 of 38 © Boardworks Ltd 2005

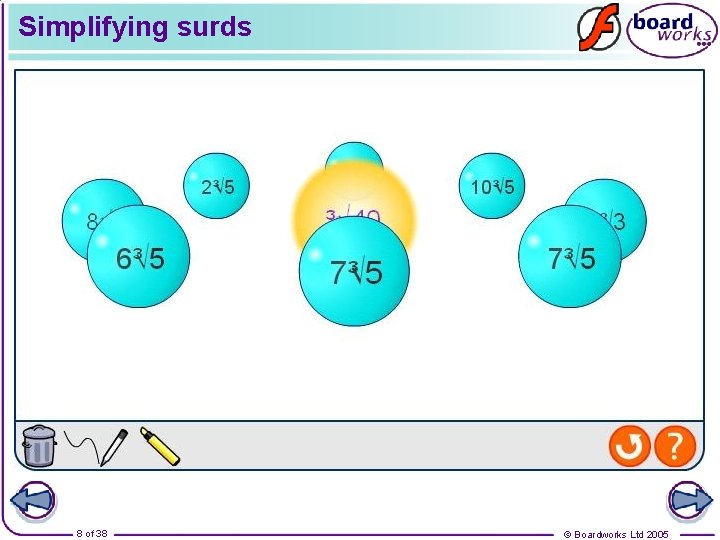
Simplifying surds We are often required to simplify surds by writing them in the form We can do this using the fact that For example: Simplify by writing it in the form Start by finding the largest square number that divides into 50. This is 25. We can use this to write: 6 of 38 © Boardworks Ltd 2005

Simplifying surds Simplify the following surds by writing them in the form a√b. 7 of 38 © Boardworks Ltd 2005

Simplifying surds 8 of 38 © Boardworks Ltd 2005

Adding and subtracting surds Surds can be added or subtracted if the number under the square root sign is the same. For example: Start by writing 9 of 38 and in their simplest forms. © Boardworks Ltd 2005

Expanding brackets containing surds Simplify the following: Problem 2) demonstrates the fact that (a – b)(a + b) = a 2 – b 2. In general: 10 of 38 © Boardworks Ltd 2005

Rationalizing the denominator Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 11 of 38 © Boardworks Ltd 2005

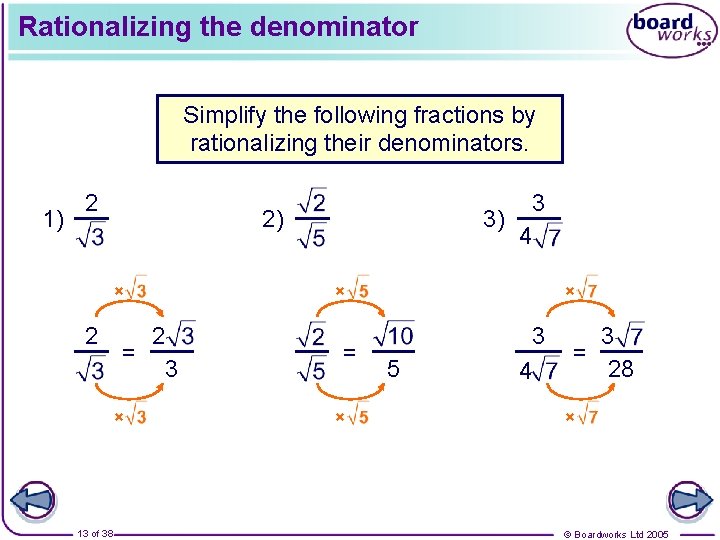
Rationalizing the denominator When a fraction contains a surd as the denominator we usually rewrite it so that the denominator is a rational number. This is called rationalizing the denominator. For example: Simplify the fraction . In this example we rationalize the denominator by multiplying the numerator and the denominator by × 5 5 = 2 × 12 of 38 © Boardworks Ltd 2005

Rationalizing the denominator Simplify the following fractions by rationalizing their denominators. 1) 2 2) × 2 2 = 3 × 13 of 38 3 3) 4 × = × × 5 3 4 3 = 28 × © Boardworks Ltd 2005

Rationalizing the denominator When the denominator involves sums of differences between surds we can use the fact that (a – b)(a + b) = a 2 – b 2 to rationalize the denominator. For example: Simplify 14 of 38 © Boardworks Ltd 2005

Rationalizing the denominator More difficult examples may include surds in both the numerator and the denominator. For example: Simplify Working: =6 15 of 38 +1 © Boardworks Ltd 2005

The index laws Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 16 of 38 © Boardworks Ltd 2005

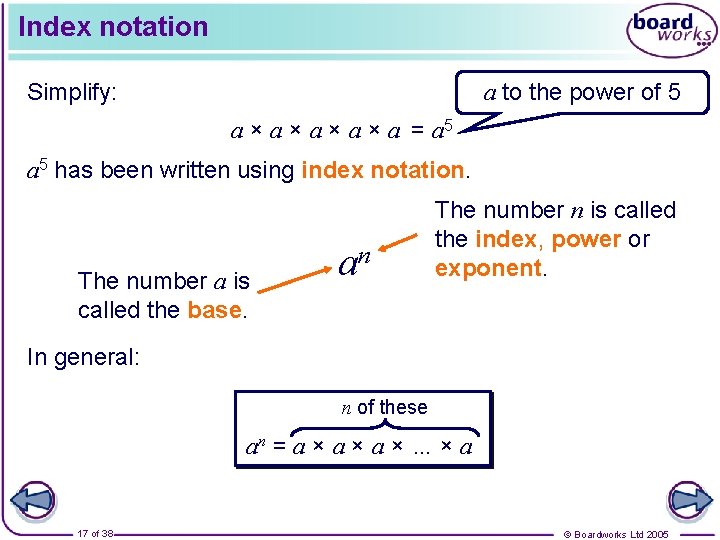
Index notation Simplify: a to the power of 5 a × a × a = a 5 has been written using index notation. The number a is called the base. an The number n is called the index, power or exponent. In general: n of these an = a × a × … × a 17 of 38 © Boardworks Ltd 2005

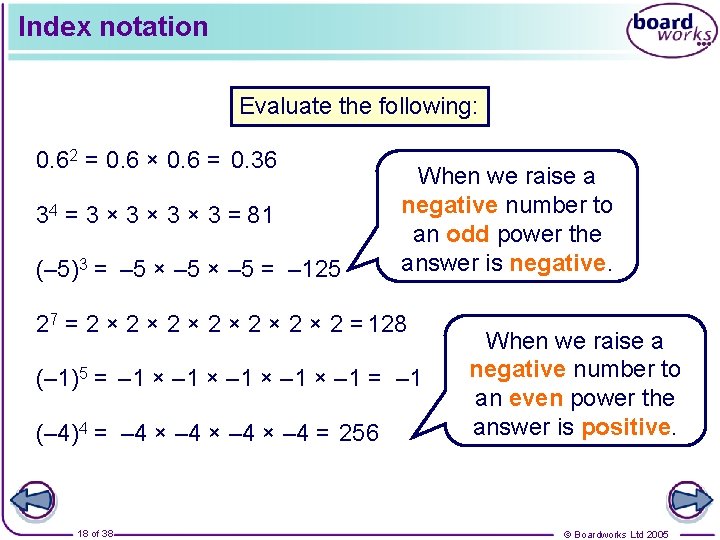
Index notation Evaluate the following: 0. 62 = 0. 6 × 0. 6 = 0. 36 34 = 3 × 3 × 3 = 81 (– 5)3 = – 5 × – 5 = – 125 When we raise a negative number to an odd power the answer is negative. 27 = 2 × 2 × 2 × 2 = 128 (– 1)5 = – 1 × – 1 = – 1 (– 4)4 = – 4 × – 4 = 256 18 of 38 When we raise a negative number to an even power the answer is positive. © Boardworks Ltd 2005

The multiplication rule When we multiply two terms with the same base the indices are added. For example: a 4 × a 2 = (a × a × a) × (a × a) =a×a×a×a = a 6 = a (4 + 2) In general: am × an = a(m + n) 19 of 38 © Boardworks Ltd 2005

The division rule When we divide two terms with the same base the indices are subtracted. For example: a 5 ÷ a 2 a×a×a = a 3 = a (5 – 2) 2 4 p 6 ÷ 2 p 4 4×p×p×p = = 2 p 2 = 2 p(6 – 4) 2×p×p In general: am ÷ an = a(m – n) 20 of 38 © Boardworks Ltd 2005

The power rule When a term is raised to a power and the result raised to another power, the powers are multiplied. For example: (y 3)2 = y 3 × y 3 (pq 2)4 = pq 2 × pq 2 = (y × y) × (y × y) = p 4 × q (2 + 2 + 2) = y 6 = y 3× 2 = p 4 × q 8 = p 4 q 8 = p 1× 4 q 2× 4 In general: (am)n = amn 21 of 38 © Boardworks Ltd 2005

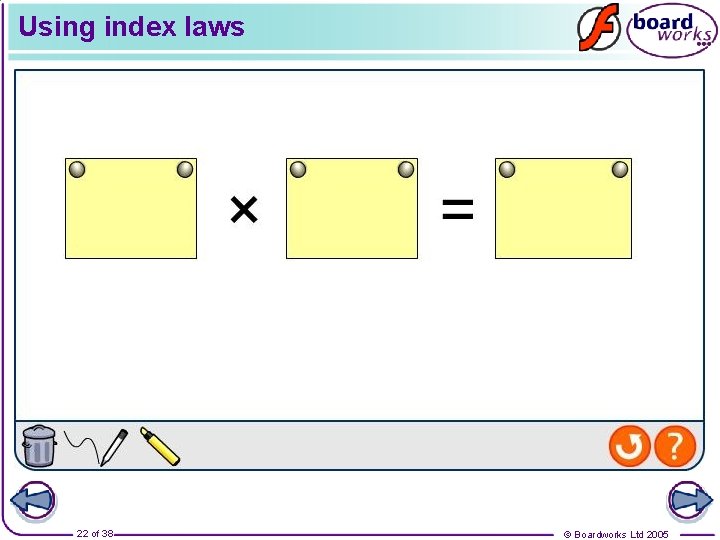
Using index laws 22 of 38 © Boardworks Ltd 2005

Zero and negative indices Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 23 of 38 © Boardworks Ltd 2005

The zero index Any number or term divided by itself is equal to 1. Look at the following division: y 4 ÷ y 4 = 1 But using the rule that xm ÷ xn = x(m – n) y 4 ÷ y 4 = y(4 – 4) = y 0 That means that y 0 = 1 In general: a 0 = 1 24 of 38 (for all a ≠ 0) © Boardworks Ltd 2005

Negative indices Look at the following division: b 2 ÷ b 4 = b×b×b×b 1 1 = = 2 b×b b But using the rule that am ÷ an = a(m – n) b 2 ÷ b 4 = b(2 – 4) = b– 2 That means that b– 2 = 1 b 2 In general: a–n = 25 of 38 1 an © Boardworks Ltd 2005

Negative indices Write the following using fraction notation: 1) u– 1 = This is the reciprocal of u. 2) 2 n– 4 = 3) x 2 y– 3 = 4) 5 a(3 – b)– 2 = 26 of 38 © Boardworks Ltd 2005

Negative indices Write the following using negative indices: 2 a– 1 x 3 y– 4 p 2(q + 2)– 1 3 m(n 2 – 5)– 3 27 of 38 © Boardworks Ltd 2005

Fractional indices Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 28 of 38 © Boardworks Ltd 2005

Fractional indices Indices can also be fractional. For example: What is the meaning of ? Using the multiplication rule: = a 1 =a But is the square root of a. So 29 of 38 © Boardworks Ltd 2005

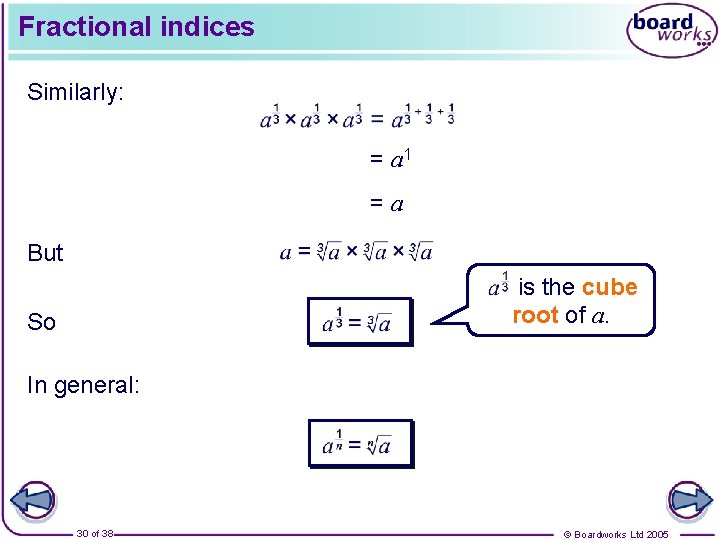
Fractional indices Similarly: = a 1 =a But is the cube root of a. So In general: 30 of 38 © Boardworks Ltd 2005

Fractional indices What is the meaning of ? We can write Using the rule that (am)n = amn, we can write We can also write In general: or 31 of 38 © Boardworks Ltd 2005

Fractional indices Evaluate the following: 32 of 38 © Boardworks Ltd 2005

Summary of the index laws Here is a summary of the index laws for all rational exponents: 33 of 38 © Boardworks Ltd 2005

Solving equations involving indices Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 34 of 38 © Boardworks Ltd 2005

Solving equations involving indices We can use the index laws to solve certain types of equation involving indices. For example: Solve the equation 25 x = 1255 – x (52)x = (53)5 – x 52 x = 53(5 – x) 2 x = 15 – 3 x 5 x = 15 x=3 35 of 38 © Boardworks Ltd 2005

Examination-style questions Contents Using and manipulating surds Rationalizing the denominator The index laws Zero and negative indices Fractional indices Solving equations involving indices Examination-style questions 36 of 38 © Boardworks Ltd 2005

Examination-style question 1 a and b are integers. Hence find the values of a and b. Multiplying top and bottom by So 37 of 38 a = 3 and gives b=2 © Boardworks Ltd 2005

Examination-style question 2 a) Express 32 x in the form 2 ax where a is an integer to be determined. b) Use your answer to part a) to solve the equation a) 32 = 25 So 32 x = (25)x Using the rule that (am)n = amn 32 x = 25 x b) Using the answer from part a) this equation can be written as 5 x = x 2 5 x – x 2 = 0 x (5 – x) = 0 x = 0 or x = 5 38 of 38 © Boardworks Ltd 2005
 Hypothesis testing a level maths
Hypothesis testing a level maths Pie charts questions
Pie charts questions Fermi estimation core maths
Fermi estimation core maths Core 4 maths
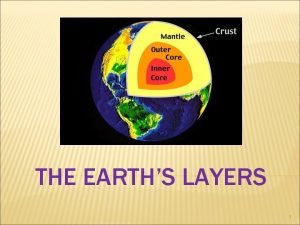
Core 4 maths Compare and contrast the crust mantle and core
Compare and contrast the crust mantle and core Crust outer core inner core mantle
Crust outer core inner core mantle Core rigidity
Core rigidity Inner core and outer core
Inner core and outer core Shingelfrisyren
Shingelfrisyren Byggprocessen steg för steg
Byggprocessen steg för steg Karttecken brant
Karttecken brant Biologiska arvet
Biologiska arvet Rådet för byggkompetens
Rådet för byggkompetens Vätsketryck formel
Vätsketryck formel Elektronik för barn
Elektronik för barn Vad är densitet
Vad är densitet Tack för att ni har lyssnat
Tack för att ni har lyssnat Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Jiddisch
Jiddisch Typiska novell drag
Typiska novell drag Mjälthilus
Mjälthilus Frgar
Frgar Större och mindre tecken
Större och mindre tecken Magnetsjukhus
Magnetsjukhus Indikation för kejsarsnitt på moderns önskan
Indikation för kejsarsnitt på moderns önskan Toppslätskivling effekt
Toppslätskivling effekt Redogör för vad psykologi är
Redogör för vad psykologi är Borra hål för knoppar
Borra hål för knoppar En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Bra mat för unga idrottare
Bra mat för unga idrottare Lek med former i förskolan
Lek med former i förskolan Bris för vuxna
Bris för vuxna Ledarskapsteorier
Ledarskapsteorier Svenskt ramverk för digital samverkan
Svenskt ramverk för digital samverkan Antika plagg
Antika plagg Datorkunskap för nybörjare
Datorkunskap för nybörjare Rita perspektiv
Rita perspektiv Ministerstyre för och nackdelar
Ministerstyre för och nackdelar Sju principer för tillitsbaserad styrning
Sju principer för tillitsbaserad styrning