ASLevel Maths Mechanics 1 for Edexcel M 1

AS-Level Maths: Mechanics 1 for Edexcel M 1. 3 Kinematics These icons indicate that teacher’s notes or useful web addresses are available in the Notes Page. This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 37 © Boardworks Ltd 2005

Contents Motion graphs Formulae for constant acceleration Examination-style questions 2 of 37 © Boardworks Ltd 2005

Kinematics involves the study of how things move. It is only concerned with the motion itself, not the forces that cause this motion. The kinematics of an object is described in terms of its distance, displacement, speed, velocity, acceleration. 3 of 37 © Boardworks Ltd 2005

Distance and displacement Distance is a scalar quantity. The distance a body has travelled is literally the amount of ‘ground’ it has covered during its motion. Displacement is a vector quantity. Displacement describes how far a body is from its starting point and in what direction. Distance and displacement are measured in metres, m. 4 of 37 © Boardworks Ltd 2005

Speed, velocity and acceleration Speed is a scalar quantity. The speed of a body relates to how fast the body is travelling. Velocity is a vector quantity. The velocity of a body relates to how fast the body is travelling and in what direction. It is the rate at which a body changes its position. Speed and velocity are measured in metres per second, ms– 1. Acceleration can be a scalar or a vector quantity. Acceleration is the rate of change of speed or velocity. It is measured in metres per second, ms– 2. Negative acceleration is often called deceleration or retardation. 5 of 37 © Boardworks Ltd 2005

Motion graphs The kinematics of a body can be represented graphically. The most common graphs are position-time, speed-time, velocity-time and acceleration-time graphs. The gradient of a distance-time graph gives speed. The gradient of a displacement-time graph gives velocity. The gradient of a velocity-time graph gives acceleration. The area under a speed-time graph gives the distance travelled. The area under a velocity-time graph gives the change in displacement. The area under an acceleration-time graph gives the change in velocity. 6 of 37 © Boardworks Ltd 2005

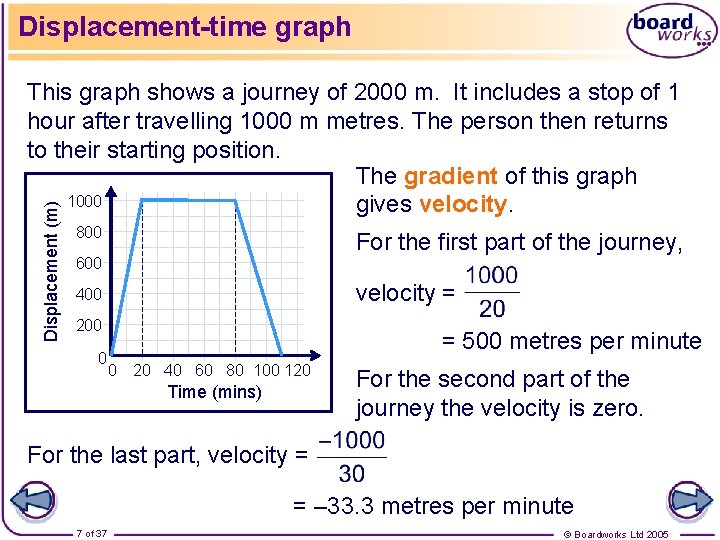
Displacement-time graph Displacement (m) This graph shows a journey of 2000 m. It includes a stop of 1 hour after travelling 1000 m metres. The person then returns to their starting position. The gradient of this graph 1000 gives velocity. 800 For the first part of the journey, 600 velocity = 400 200 0 = 500 metres per minute 0 20 40 60 80 100 120 Time (mins) For the second part of the journey the velocity is zero. For the last part, velocity = = – 33. 3 metres per minute 7 of 37 © Boardworks Ltd 2005

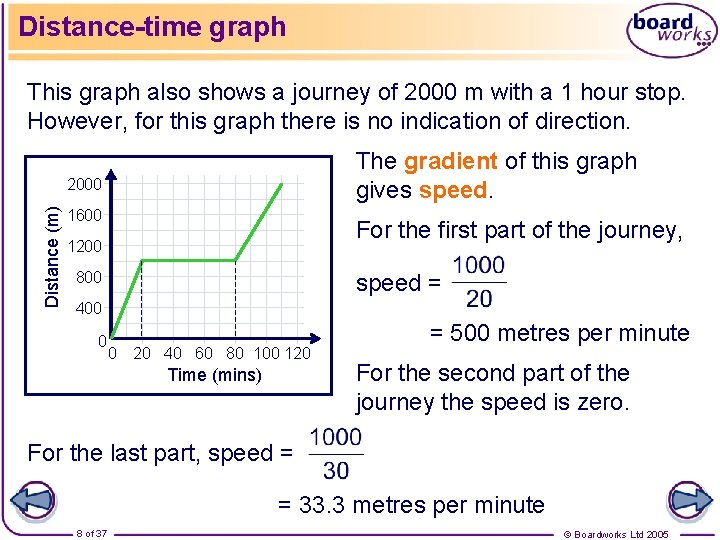
Distance-time graph This graph also shows a journey of 2000 m with a 1 hour stop. However, for this graph there is no indication of direction. The gradient of this graph gives speed. Distance (m) 2000 1600 For the first part of the journey, 1200 800 speed = 400 0 0 20 40 60 80 100 120 Time (mins) = 500 metres per minute For the second part of the journey the speed is zero. For the last part, speed = = 33. 3 metres per minute 8 of 37 © Boardworks Ltd 2005

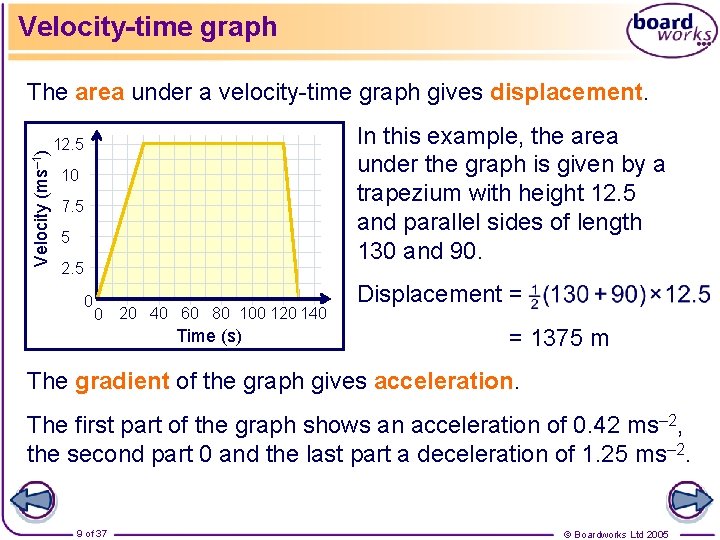
Velocity-time graph Velocity (ms– 1) The area under a velocity-time graph gives displacement. In this example, the area under the graph is given by a trapezium with height 12. 5 and parallel sides of length 130 and 90. 12. 5 10 7. 5 5 2. 5 0 0 20 40 60 80 100 120 140 Time (s) Displacement = = 1375 m The gradient of the graph gives acceleration. The first part of the graph shows an acceleration of 0. 42 ms– 2, the second part 0 and the last part a deceleration of 1. 25 ms– 2. 9 of 37 © Boardworks Ltd 2005

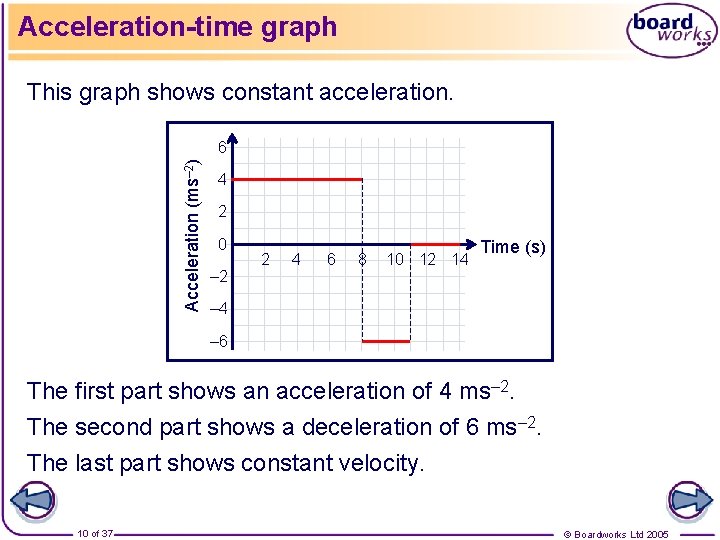
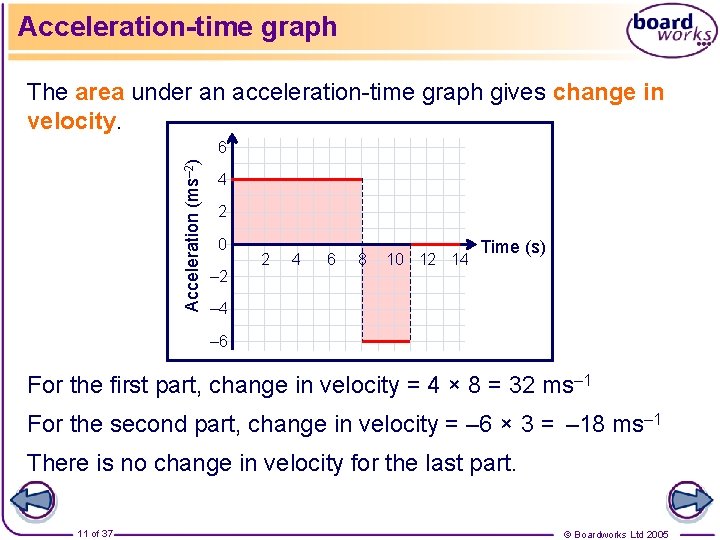
Acceleration-time graph This graph shows constant acceleration. Acceleration (ms– 2) 6 4 2 0 – 2 2 4 6 8 10 12 14 Time (s) – 4 – 6 The first part shows an acceleration of 4 ms– 2. The second part shows a deceleration of 6 ms– 2. The last part shows constant velocity. 10 of 37 © Boardworks Ltd 2005

Acceleration-time graph The area under an acceleration-time graph gives change in velocity. Acceleration (ms– 2) 6 4 2 0 – 2 2 4 6 8 10 12 14 Time (s) – 4 – 6 For the first part, change in velocity = 4 × 8 = 32 ms– 1 For the second part, change in velocity = – 6 × 3 = – 18 ms– 1 There is no change in velocity for the last part. 11 of 37 © Boardworks Ltd 2005

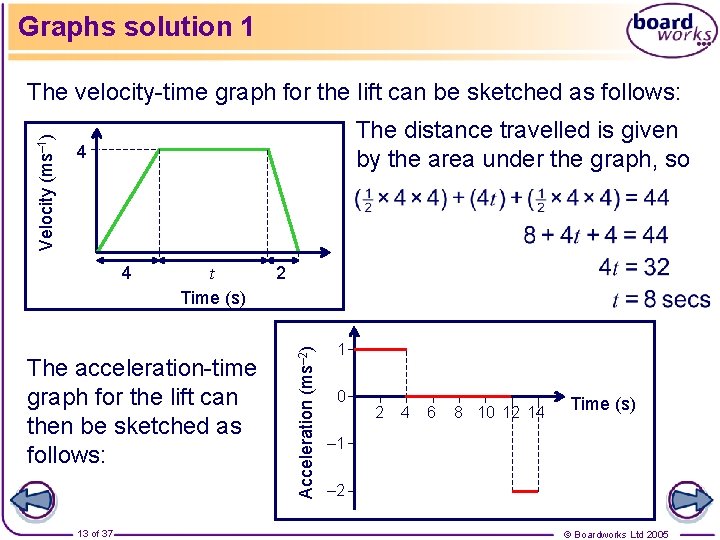
Graphs example 1 A man travels in a lift from the top floor of a hotel to reception on the ground floor. The lift accelerates with a constant acceleration of 1 ms– 2 until it reaches a constant velocity of 4 ms– 1. It then travels at this constant velocity for t seconds before decelerating with a constant deceleration of 2 ms– 2 until it reaches the ground floor. Given that the man has descended 44 m, a) sketch the velocity-time graph of the lift and use it to find t b) sketch the acceleration-time graph of the lift. 12 of 37 © Boardworks Ltd 2005

Graphs solution 1 The distance travelled is given by the area under the graph, so 4 4 t Time (s) The acceleration-time graph for the lift can then be sketched as follows: 13 of 37 2 Acceleration (ms– 2) Velocity (ms– 1) The velocity-time graph for the lift can be sketched as follows: 1 0 2 4 6 8 10 12 14 Time (s) – 1 – 2 © Boardworks Ltd 2005

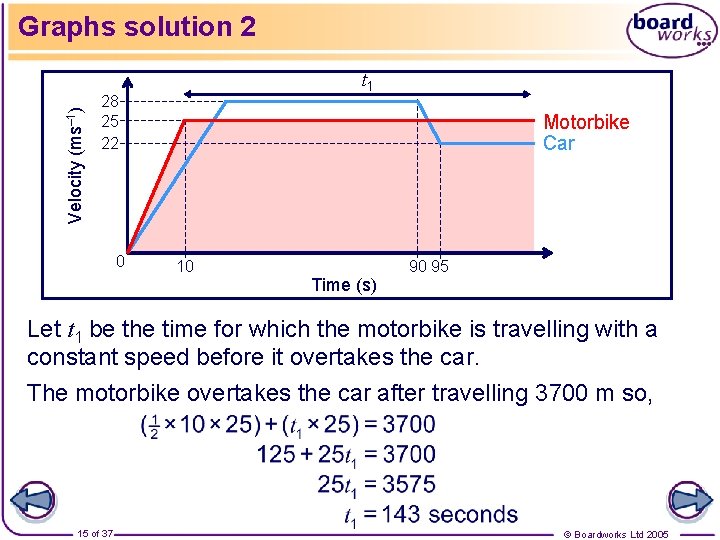
Graphs example 2 A car and a motorcycle are travelling along a straight road. The car accelerates from rest to a constant speed of 28 ms– 1. The motorcycle accelerates from rest to a constant speed of 25 ms– 1 in 10 seconds. After travelling for 90 seconds the car hits traffic and decelerates to a constant speed of 22 ms– 1 in 5 seconds. The motorcycle is unaffected by the traffic and maintains his speed. The motorcycle overtakes the car after they have both travelled 3700 m. Draw a speed-time graph and use it to find the time when the motorcycle overtakes the car and how long the car was initially accelerating for. 14 of 37 © Boardworks Ltd 2005

Velocity (ms– 1) Graphs solution 2 t 1 28 25 22 0 Motorbike Car 10 Time (s) 90 95 Let t 1 be the time for which the motorbike is travelling with a constant speed before it overtakes the car. The motorbike overtakes the car after travelling 3700 m so, 15 of 37 © Boardworks Ltd 2005

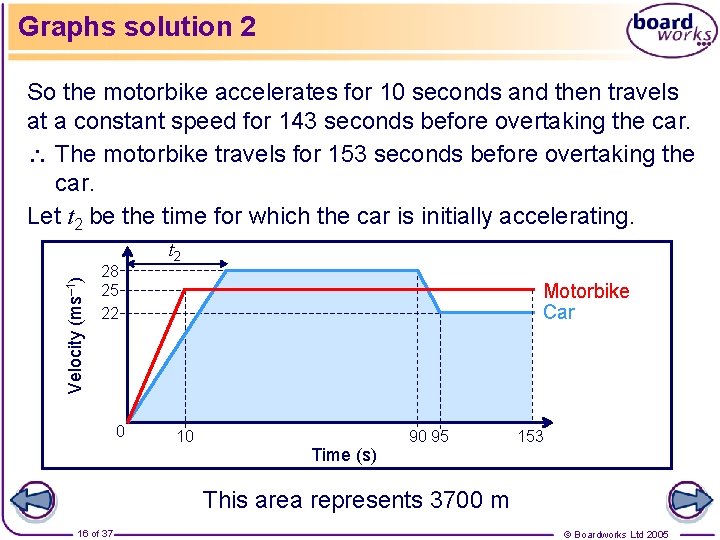
Graphs solution 2 Velocity (ms– 1) So the motorbike accelerates for 10 seconds and then travels at a constant speed for 143 seconds before overtaking the car. The motorbike travels for 153 seconds before overtaking the car. Let t 2 be the time for which the car is initially accelerating. 28 25 22 0 t 2 Motorbike Car 10 Time (s) 90 95 153 This area represents 3700 m 16 of 37 © Boardworks Ltd 2005

Graphs solution 2 Since the area under the graph for the car between 0 and 153 seconds is equal to 3700 so we can write, 14 t 2 + 2520 – 28 t 2 + 125 + 1276 = 3700 14 t 2 = 221 t 2 = 15. 8 (to 3 sf) Therefore the car was initially accelerating for 15. 8 s (to 3 s. f. ) 17 of 37 © Boardworks Ltd 2005

Contents Formulae for constant acceleration Motion graphs Formulae for constant acceleration Examination-style questions 18 of 37 © Boardworks Ltd 2005

Formulae for constant acceleration If a particle is moving in a straight line with a constant acceleration there are five equations of motion that can be used to determine missing quantities. Where s = displacement in metres u = initial velocity in ms– 1 v = final velocity in ms– 1 a = acceleration in ms– 2 t = time taken in seconds These are sometimes called the suvat formulae. For vertical motion acceleration due to gravity is g, 9. 8 ms– 2. 19 of 37 © Boardworks Ltd 2005

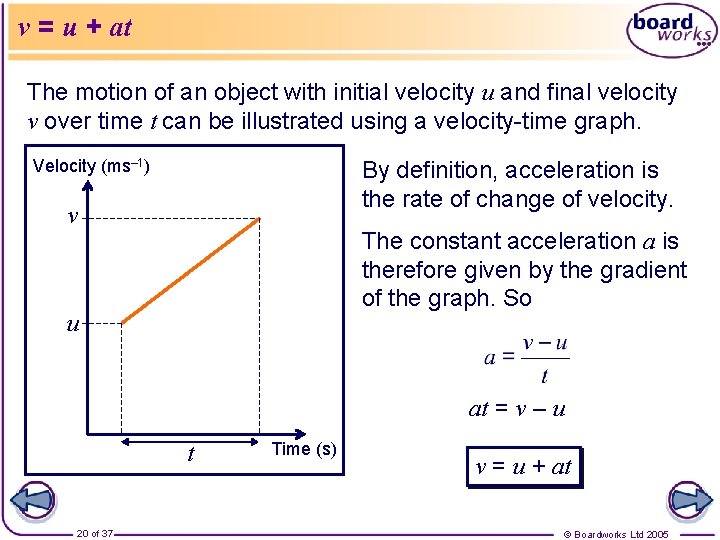
v = u + at The motion of an object with initial velocity u and final velocity v over time t can be illustrated using a velocity-time graph. Velocity (ms– 1) By definition, acceleration is the rate of change of velocity. v The constant acceleration a is therefore given by the gradient of the graph. So u at = v – u t 20 of 37 Time (s) v = u + at © Boardworks Ltd 2005

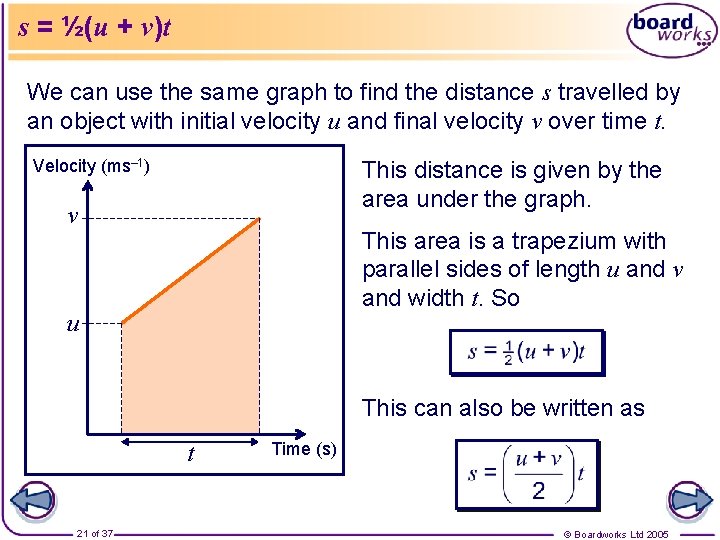
s = ½(u + v)t We can use the same graph to find the distance s travelled by an object with initial velocity u and final velocity v over time t. Velocity (ms– 1) This distance is given by the area under the graph. v This area is a trapezium with parallel sides of length u and v and width t. So u This can also be written as t 21 of 37 Time (s) © Boardworks Ltd 2005

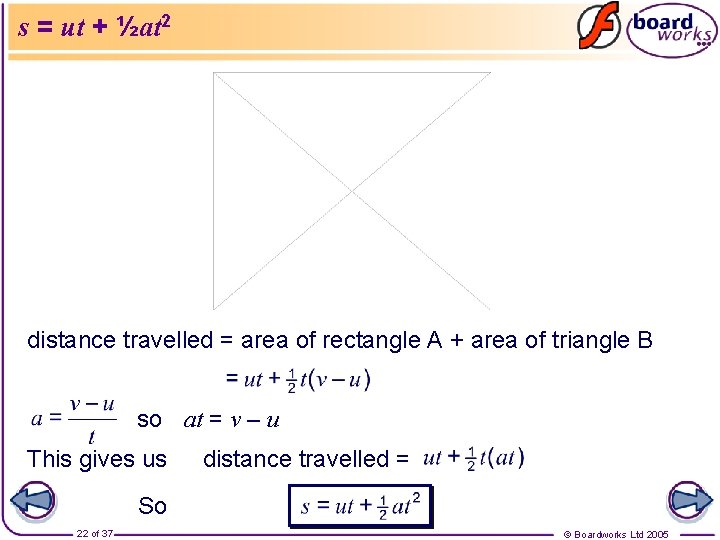
s = ut + ½at 2 distance travelled = area of rectangle A + area of triangle B so at = v – u This gives us distance travelled = So 22 of 37 © Boardworks Ltd 2005

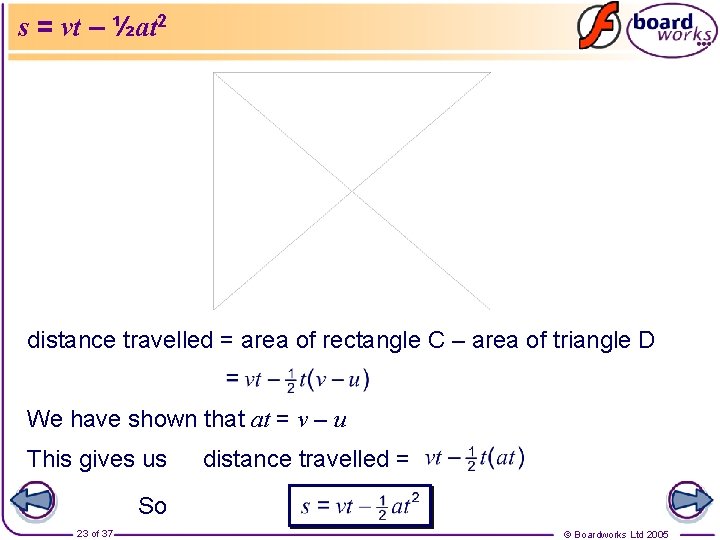
s = vt – ½at 2 distance travelled = area of rectangle C – area of triangle D We have shown that at = v – u This gives us distance travelled = So 23 of 37 © Boardworks Ltd 2005

v 2 = u 2 + 2 as We can show that v 2 = u 2 + 2 as as using v = u + at 1 2 Rearranging equation 1 to make t the subject gives Substituting this into equation 2 So 24 of 37 © Boardworks Ltd 2005

Constant acceleration example 1 A stone is thrown vertically upwards with a speed of 10 ms– 1 from a point 15 m above the ground. Find the maximum height above the ground that the stone reaches and find the time taken for the stone to reach the ground. Taking to be positive, the information given in the question is: u = 10 a = –g (Take g to be 9. 8) The question is asking for s when v = 0, and for t when s = – 15. 25 of 37 © Boardworks Ltd 2005

Constant acceleration solution 1 To calculate s when v = 0, given u and a requires the use of v 2 = u 2 + 2 as. 02 = 102 + 2(– 9. 8)(s) 0 = 100 – 19. 6 s = 100 s = 5. 10 (to 3 s. f. ) Therefore, the maximum height above the ground that the stone reaches is 20. 1 m (to 3 s. f. ). 26 of 37 © Boardworks Ltd 2005

Constant acceleration solution 1 To calculate t when s = – 15, given u and a requires the use of s = ut + at 2. – 15 = 10 t + (– 9. 8)t 2 – 15 = 10 t – 4. 9 t 2 Arranging all the terms on the left gives us the following quadratic equation 4. 9 t 2 – 10 t – 15 = 0 Using gives the solution t = 3. 05 or t = – 1. 01 (to 3 s. f. ) Therefore the stone reaches the ground after 3. 05 s (to 3 s. f. ). 27 of 37 © Boardworks Ltd 2005

Constant acceleration example 2 A particle moves in a horizontal line from a point A to a point C, via point B. It has a constant acceleration of 1 ms– 2 and passes point B after 6 seconds and point C after a further 4 seconds. Its velocity at C is 50 ms– 1. Calculate the velocity at A and the distances AB and BC. We can sketch the situation as follows A B t=6 C t = 10 v = 50 Taking to be positive the question firstly asks for u when a = 1, t = 10 and v = 50. This requires the use of v = u + at. 28 of 37 © Boardworks Ltd 2005

Constant acceleration example 2 v = u + at 50 = u + (1)(10) 50 = u + 10 u = 40 Therefore the particle passes A with a velocity of 40 ms– 1. The next part of the question asks for s when u = 40, a = 1 and t = 6, requiring the use of s = ut + at 2 s = 40(6) + (1)(6)2 s = 240 + 18 = 258 Therefore AB is 258 m. 29 of 37 © Boardworks Ltd 2005

Constant acceleration example 2 The final part of the question asks for s when u = 40, a = 1 and t = 10, again requiring the use of s = ut + at 2 s = 40(10) + (1)(10)2 s = 400 + 50 = 450 Therefore AC is 450 m and so BC is 192 m. 30 of 37 © Boardworks Ltd 2005

Constant acceleration example 3 A ball falls off a cliff and lands on the beach 3. 2 seconds later. How high is the cliff? Taking to be positive the information given in the question is a = 9. 8 t = 3. 2 u=0 To calculate s requires the use of the formula s = ut + at 2 s = (0)(3. 2) + (9. 8)(3. 2)2 s = 50. 2 (to 3 s. f ) Therefore the height of the cliff is 50. 2 m (to 3 s. f. ) 31 of 37 © Boardworks Ltd 2005

Contents Examination-style questions Motion graphs Formulae for constant acceleration Examination-style questions 32 of 37 © Boardworks Ltd 2005

Examination-style question 1 A ball is thrown vertically upwards with an initial velocity of ms– 1 from a point 1. 2 m above the ground. It reaches a maximum height of 23 m above the ground. Calculate a) the initial velocity b) the velocity with which the ball strikes the ground c) the total time the ball is in the air. 33 of 37 © Boardworks Ltd 2005 u

Solution 1 a) Taking as positive, v = 0, s = 21. 8, a = – 9. 8 v 2 = u 2 + 2 as 0 = u 2 + 2(-9. 8)(21. 8) 0 = u 2 – 427. 28 u = ± 427. 28 (to 3 s. f. ) initial velocity is 20. 7 ms– 1 (to 3 s. f. ) b) Method 1 - Using downward motion only Taking to be positive, u = 0, a = 9. 8, s = 23 v 2 = u 2 + 2 as v 2 = 02 + 2(9. 8)(23) v 2 = 450. 8 v = ± 21. 2 (to 3 s. f. ) 34 of 37 The ball hits ground with a velocity of 21. 2 ms– 1 (to 3 s. f. ) © Boardworks Ltd 2005

Solution 1 b) Method 2 – Using whole motion Taking to be positive, u = – 427. 28, a = 9. 8, s = 1. 2 v 2 = u 2 + 2 as v 2 = 427. 28 + 2(9. 8)(1. 2) v 2 = 450. 8 v = 21. 2 (to 3 s. f. ) ball strikes ground with a velocity of 21. 2 ms-1 (to 3 s. f. ) c) Taking as positive, u = – 427. 28, v = 450. 8, a = 9. 8 v = u + at t = 4. 28 (to 3 s. f. ) ball is in the air for 4. 28 s (to 3 s. f. ) 35 of 37 © Boardworks Ltd 2005

Examination-style question 2 A car is travelling with a uniform acceleration along a straight road. It passes a point A with a velocity of 8 ms– 1 and 5 seconds later it passes a point B with velocity 25 ms– 1. Find the velocity with which the car passes the mid-point of AB. The distance AB needs to be found first: u = 8, v = 25, t = 5 s = (u + v)t s = (8 + 33)(5) s = 82. 5 the distance AB is 82. 5 m and so the mid-point of AB is at a distance of 41. 25 m from A. 36 of 37 © Boardworks Ltd 2005

Solution 2 Acceleration now needs to be found: u = 8, v = 25, t = 5 v = u + at a = 3. 4 the acceleration of the car is 3. 4 ms– 2. The velocity of the car as it passes the mid-point of AB can now be found: u = 8, a = 3. 4, s = 41. 25 v 2 = u 2 + 2 as v 2 = 82 + 2(3. 4)(41. 25) = 344. 5 v = ± 344. 5 the car passes the mid-point of AB with a velocity of 18. 6 ms– 1 (to 3 s. f. ) 37 of 37 © Boardworks Ltd 2005