1 12 1 Rounding Modes 2 Rounding the

1

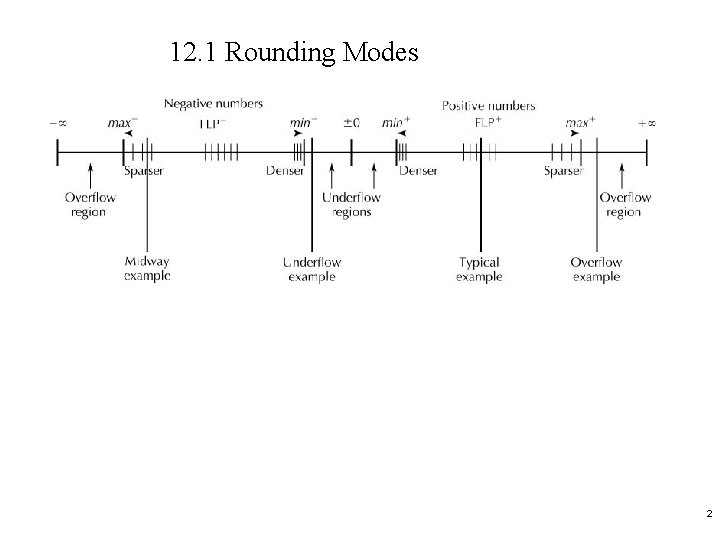
12. 1 Rounding Modes 2

Rounding: the process to obtain the best possible floating-point representation for a given real value. ANSI/IEEE standard: round to floating number whose significand has an LSB of 0 (of two adjacent floatingpoint number, the significand of one must end in 0, and the other one in 1). This is called round-to-neareven. For example, 3. 5 and 4. 5 are both rounded to 4, the closet even number, based on round-to-near-even. 3

• Other rounding methods – Round inward (toward 0): choose the nearest value in the same direction as 0. – Round upward (toward +∞): choose the larger of the two possible values. – Round downward (toward -∞): choose the smaller of the two possible vavlues. • 4

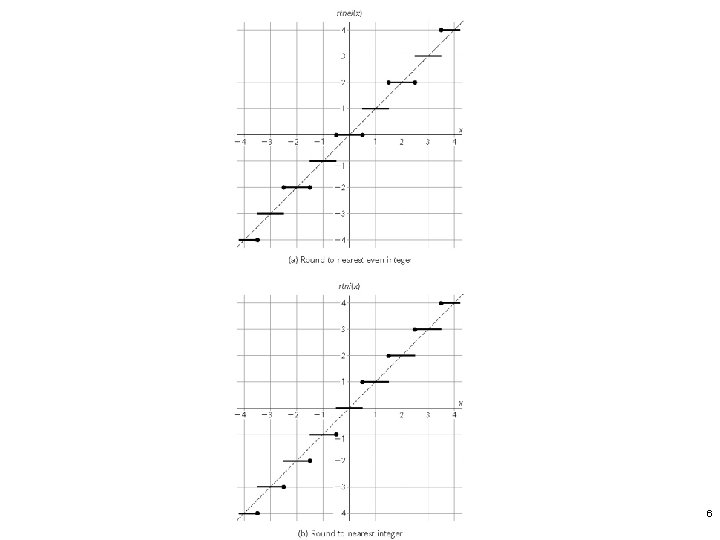
Example 12. 1 Rounding to the nearest integer a. Consider the rounded even integer corresponding to a real signed-magnitude number x a rtnei(x). Plot this round-tonearest-even-integer for x in the range [-4, 4]. b. Repeat part a for the function rtni(x), that is, round-to-nearest-integer function, where the midway values are always rounded up 5

6

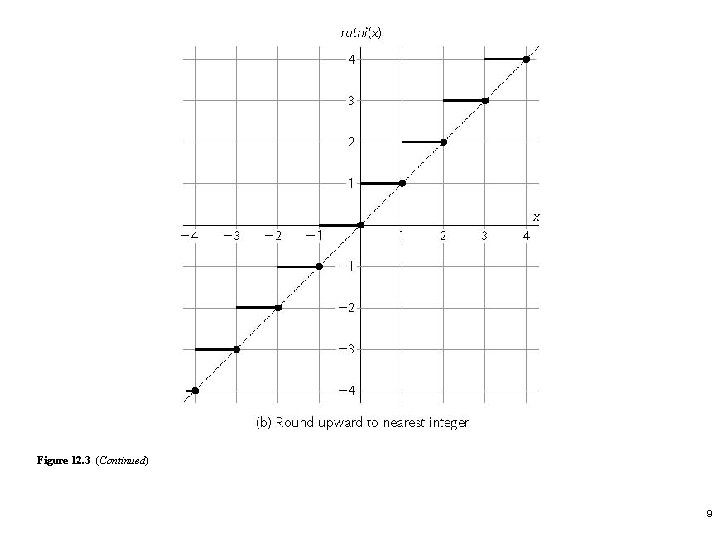
Example 12. 2 Directed rounding a. Consider the inward-directed round corresponding to a real signed-magnitude number x as a function ritni(x). Plot this round-inward-to-nearest-integer function for x in the range [-4, 4]. b. Repeat part a for the round-upward-to-nearest -integer rutni(x). 7

Figure 12. 3 Two directed round-to-nearest-integer functions for x in [– 4, 4]. 8

Figure 12. 3 (Continued) 9

12. 2 Special Values and Execeptions • Five special values in ANSI/IEEE floating-point standard – ± 0 Biased exponent=0, significand=0 (no hidden 1) –±∞ Biased exponent=255 (short), or 2047 (long), significand=0 – Na. N Biased exponent=255 (short), or 2047 (long), significand≠ 0 10

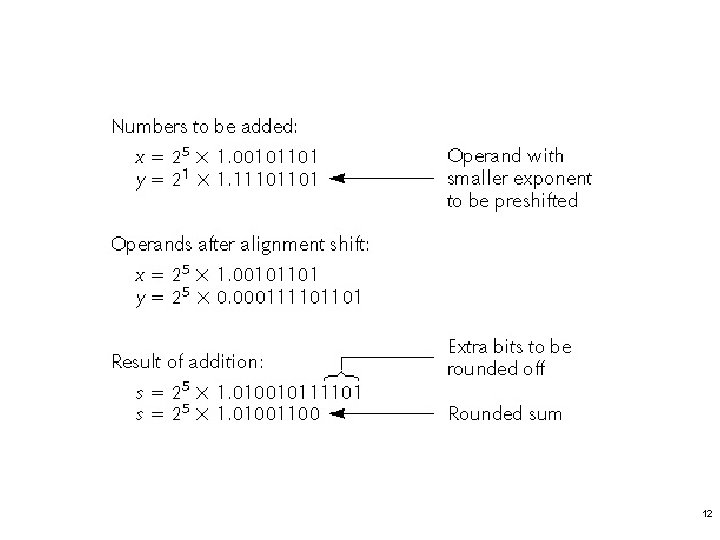
12. 3 Floating-Point Addition Consider the addition of ± 2 e 1 s 1 and ± 2 e 2 s 2, where e 1 > e 2 (± 2 e 1 s 1) +(± 2 e 2 s 2)=± 2 e 1(s 1±s 2/2 e 1 -e 2) 11

12

Figure 12. 6 Simplified schematic of a floating-point adder 13

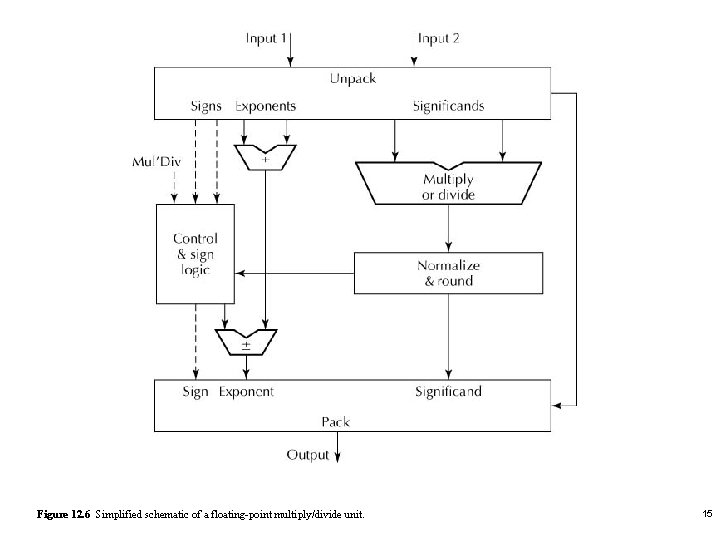
12. 4 Other Floating-point Operations Multiplication of ± 2 e 1 s 1 and ± 2 e 2 s 2 (± 2 e 1 s 1)×(± 2 e 2 s 2)=± 2 e 1+e 2(s 1×s 2/2 e 1 -e 2) Division of ± 2 e 1 s 1 and ± 2 e 2 s 2 (± 2 e 1 s 1)/(± 2 e 2 s 2)=± 2 e 1 -e 2(s 1/s 2) 14

Figure 12. 6 Simplified schematic of a floating-point multiply/divide unit. 15

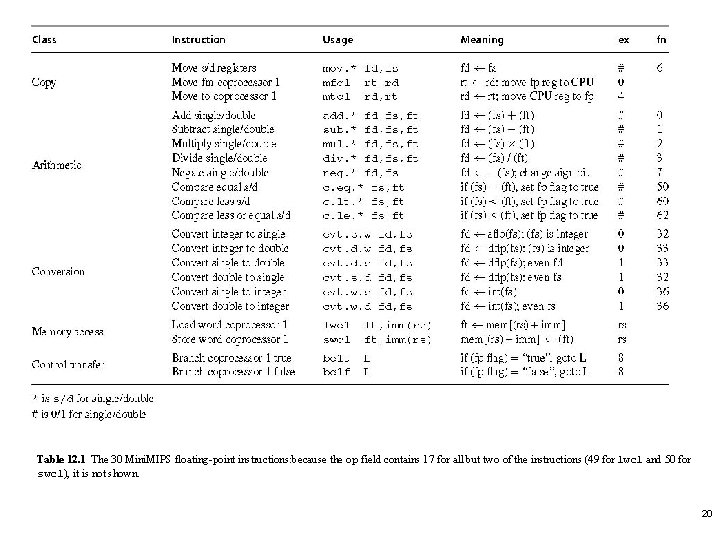
12. 5 Floating-Point Instructions 10 floating-point arithmetic instructions (5 different operations: add, sub, multiply, divide, negate) add. s $f 0, $f 8, $f 10 # set $f 0 to ($f 8)+($f 10) add. d $f 0, $f 8, $f 10 # set $f 0 $f 1 to ($f 8$f 9)+($f 10$f 11) Single operands can be in any of the floating registers. Double operands must be in specified to be in even numbered registers Figure 12. 7 The common floating-point instruction format for Mini. MIPS and components for arithmetic instructions. The extension (ex) field distinguishes single (* = s) from double (* = d) operands. 16

6 format conversion instructions: integer to single/double, single to double, double to single, and single/double to integer cvt. s. w $f 0, $f 8 cvt. d. s $f 0, $f 8 cvt. s. d $f 0, $f 8 cvt. w. s $f 0, $f 8 cvt. w. d $f 0, $f 8 # set $f 0 to single (integer $f 8) # set $f 0 to double ($f 8) # set $f 0 to single ( $f 8, $f 9, ) # set $f 0 to integer ($f 8, $f 9) Figure 12. 8 Floating-point instructions format conversion in Mini. MIPS. 17

6 data transfer instructions: load/store word to/from coprocessor 1, move single/double from one FP register to another, move (copy) between FP registers and CPU general registers. lwcl $f 8, 40($3) # load mem[40+($s 3)] into $f 8 swc 1 $f 8, A($3) # store mem[A+($s 3)] into $f 8 mv. s $f 0, $f 8 # load $f 0 with ($f 8) mv. d $f 0, $f 8 # load $f 0, $f 1 with ( $f 8, $f 9, ) mfc 1 $t 0, $f 12 # load $t 0 with ($f 12) mtc 1 $f 8, $t 4 # load $f 8 with ($t 4) Figure 12. 9 Instructions for floating-point data movement in Mini. MIPS. 18

2 branch and 6 comparison instructions. The FP unit has a flag that is set to T or F based on 6 comparisons (equal, less than, or less or equal for single/double data type) bc 1 t L # branch on FP flag true bc 1 f L # branch on FP flag false c. eq. * $f 0, $f 8 # if ($f 0)=($f 8), set flag to true c. lt. * $f 0, $f 8 # if ($f 0)<($f 8), set flag to true c. lw. * $f 0, $f 8 # if ($f 0)≤($f 8), set flag to true Figure 12. 10 Floating-point branch and comparison instructions in Mini. MIPS. 19

Table 12. 1 The 30 Mini. MIPS floating-point instructions: because the op field contains 17 for all but two of the instructions (49 for lwc 1 and 50 for swc 1), it is not shown. 20

12. 6 Result Precision and Errors • FP arithmetic can be quite dangerous and must be used with proper care, because results of FP computations are inexact. • Why? – Many real numbers do not have exact binary representation within a finite word format. This is referred as representation error. – Even for values that are exactly representable, FP arithmetic produces inexact results. For example, product of 2 short FP numbers will have a 48 bits significant that must be rounded to 23 bits (plus hidden 1) This is called computation error. 21

Example 12. 4 Associate law of addition does not hold in general in FP arithmetic. For example a= -25×(1. 10101011) b=25 × (1. 10101110) c=-2 -2 × (1. 01100101) (a+b)+c = a+(b+c) ? 22

Figure 12. 11 Algebraically equivalent computations may yield different results with floating-point arithmetic. 23

• Using guard digits to avoid excessive error. For example, in a 10 -digit calculator, 1/3 is represented as 0. 333 333 3, multiplying 3 results in 0. 999 999 9, but not 1. However, in a calculator with 2 guard bits, 1/3 is represented as 0. 333 333, but still displayed as 0. 333 333 3, multiplying 3 results in 1. 24

Figure 12. 12 Function evaluation by table lookup and linear interpolation. 25