WYKAD 7 Numeryczne metody interpolacji Ryszard Myhan ZADANIA

WYKŁAD 7 Numeryczne metody interpolacji Ryszard Myhan

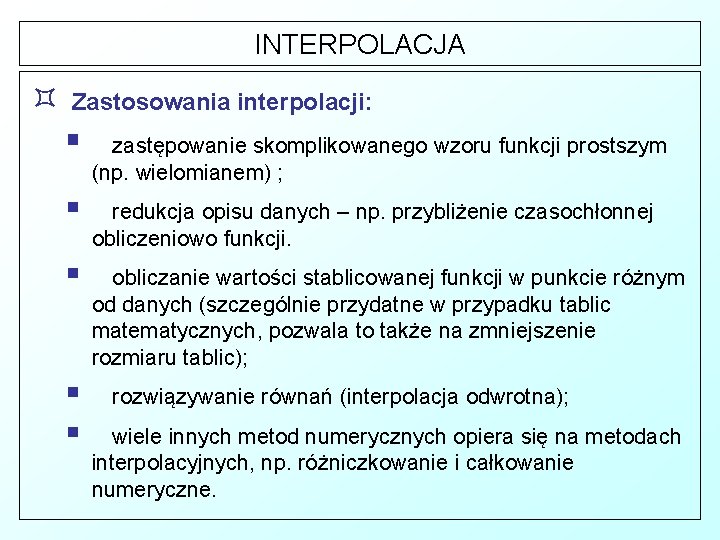
ZADANIA PRZYBLIŻENIA WIELOMIANOWEGO Interpolacja Ekstrapolacja Aproksymacja Wielomian stopnia N-1 przechodzący przez N zadanych punktów (węzłów) xi. Poszukiwane wartości y pomiędzy skrajnymi węzłami. Poszukiwane wartości y poza zakresem węzłów. Wielomian stopnia <N-1 dopasowany do N zadanych punktów wg określonego kryterium. Poszukiwane wartości y wg zależności dopasowanej.

INTERPOLACJA ³ Interpolacja jest to wyznaczenie takiej funkcji, która w jak najlepszym stopniu przedstawi inną stablicowaną nieznaną funkcje. Ä Interpolacje stosuje się w głównie do wyznaczenia wykresów funkcji określonych na dyskretnym zbiorze argumentów lub punktów będących wynikiem pomiarów i doświadczeń. Ä Przybliżenie to zachowuje równość wartości w wybranych punktach (zwanych węzłami) pomiędzy funkcją którą chcemy przybliżyć (interpolowaną), a funkcją przybliżającą (interpolującą) Ä Zazwyczaj zależy nam dodatkowo, aby w punktach które nie są węzłami przybliżenie było również jak najlepsze. Ä Jako funkcje interpolujące najczęściej wykorzystuje się wielomiany algebraiczne lub funkcje wymierne.

INTERPOLACJA ³ Zastosowania interpolacji: § zastępowanie skomplikowanego wzoru funkcji prostszym (np. wielomianem) ; § redukcja opisu danych – np. przybliżenie czasochłonnej obliczeniowo funkcji. § obliczanie wartości stablicowanej funkcji w punkcie różnym od danych (szczególnie przydatne w przypadku tablic matematycznych, pozwala to także na zmniejszenie rozmiaru tablic); § § rozwiązywanie równań (interpolacja odwrotna); wiele innych metod numerycznych opiera się na metodach interpolacyjnych, np. różniczkowanie i całkowanie numeryczne.

NAJPROSTSZE ZADANIE INTERPOLACJI Ø Poszukujemy liniowej zależności y = ax + b (nieznane a i b) między punktami (x 1 , y 1) i (x 2 , y 2). Ø W zapisie macierzowym: Ø Rozwiązanie: Ä postać Newtona: Ä postać Lagrange’a:

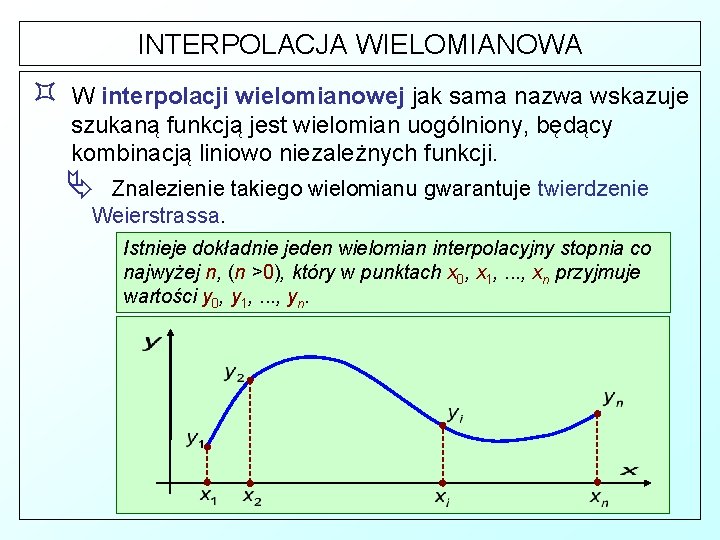
INTERPOLACJA WIELOMIANOWA ³ W interpolacji wielomianowej jak sama nazwa wskazuje szukaną funkcją jest wielomian uogólniony, będący kombinacją liniowo niezależnych funkcji. Ä Znalezienie takiego wielomianu gwarantuje twierdzenie Weierstrassa. Istnieje dokładnie jeden wielomian interpolacyjny stopnia co najwyżej n, (n >0), który w punktach x 0, x 1, . . . , xn przyjmuje wartości y 0, y 1, . . . , yn.

INTERPOLACJA WIELOMIANOWA ¥ Ogólne sformułowanie zadania interpolacji wielomianowej § Poszukujemy współczynników a wielomianu y(x), który w punktach x 1, … , x. N będzie miał wartości y 1, … , y. N : i § Wynikający z tego sformułowania układ równań : Ä układ ten posiada dokładnie tylko jedno rozwiązanie, które przyjmujemy jako współczynniki szukanego wielomianu interpolacyjnego. ¥ Wyznaczenie rozwiązania tego układu nie jest zadaniem łatwym ze względu na jego niekorzystne uwarunkowanie i kumulacje błędów.

INTERPOLACJA LAGRANGE'A ³ Zamiast rozwiązywać powyższy układ równań stosuje się tzw. wielomian interpolacyjny Lagrange'a. Ä Pozwala on na wyznaczenie małym nakładem pracy wartości tego wielomianu (bez znajomości jego współczynników) w dowolnym punkcie przedziału. ð Uogólniając postać kombinacyjną wielomianu na przypadek interpolacji N-punktowej uzyskujemy: ð Każdy Lk jest wielomianem stopnia N-1:

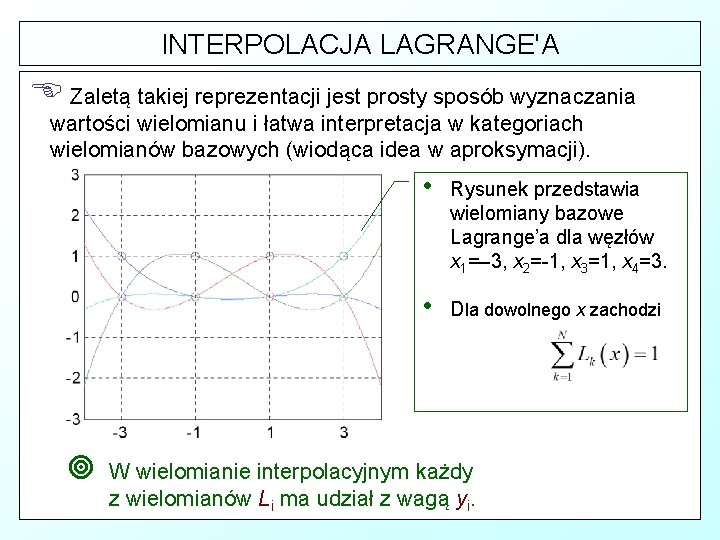
INTERPOLACJA LAGRANGE'A E Zaletą takiej reprezentacji jest prosty sposób wyznaczania wartości wielomianu i łatwa interpretacja w kategoriach wielomianów bazowych (wiodąca idea w aproksymacji). ¥ • Rysunek przedstawia wielomiany bazowe Lagrange’a dla węzłów x 1=– 3, x 2=-1, x 3=1, x 4=3. • Dla dowolnego x zachodzi W wielomianie interpolacyjnym każdy z wielomianów Li ma udział z wagą yi.

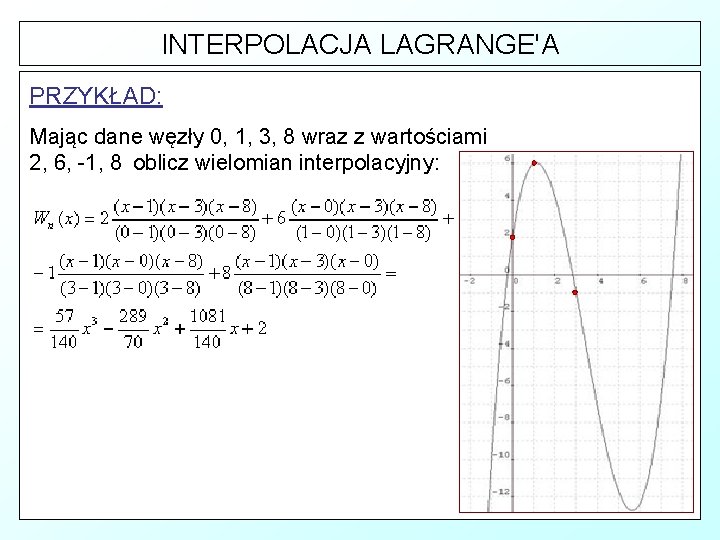
INTERPOLACJA LAGRANGE'A PRZYKŁAD: Mając dane węzły 0, 1, 3, 8 wraz z wartościami 2, 6, -1, 8 oblicz wielomian interpolacyjny:

ITERACYJNA METODA AITKENA ³ Istnieje metoda obliczania wartości wielomianu Lagrange'a w zadanym punkcie, bez obliczania samego wielomianu interpolacyjnego - służy do tego iteracyjna metoda Aitkena. § Oznaczając przez Wi, j wielomian który w węzłach xi, xj (i j) przyjmuje wartości f(xi), f(xj): § Aby obliczyć wartość wielomianu interpolacyjnego opartego na n węzłach w dowolnym punkcie x różnym od węzłów, należy obliczyć wartość W 1, 2, … , n.

ITERACYJNA METODA AITKENA § Wszystkie wyniki niezbędnych obliczeń wygodnie jest umieścić w macierzy trójkątnej wraz z węzłami oraz ich wartościami (schemat Aitkena). § Rozwiązanie takie jest dogodne zarówno podczas rachunków ręcznych, jak i maszynowych, gdyż podczas obliczania każdej wartości zawsze korzystamy z wartości położonych na lewo w tym samym rzędzie i powyższych.

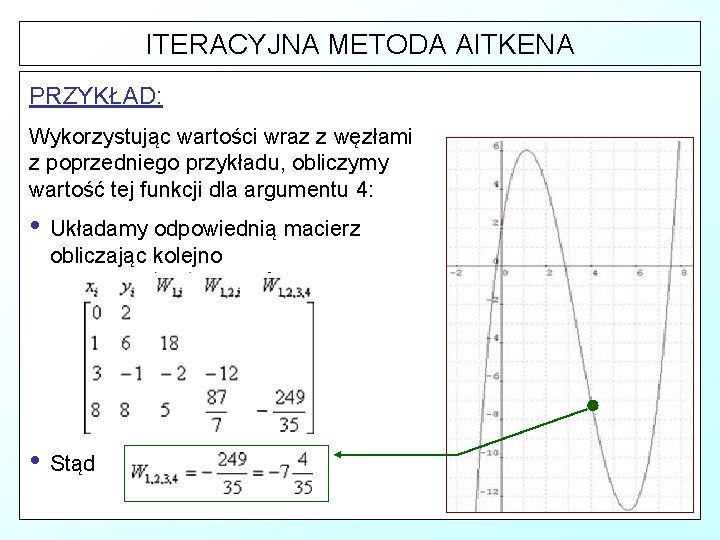
ITERACYJNA METODA AITKENA PRZYKŁAD: Wykorzystując wartości wraz z węzłami z poprzedniego przykładu, obliczymy wartość tej funkcji dla argumentu 4: • Układamy odpowiednią macierz obliczając kolejno • Stąd

INTERPOLACJA NEWTONA ³ W interpolacji Newtona jako bazę funkcji wielomianu uogólnionego wykorzystuje się ciąg wielomianów Newtona: § Wielomian interpolacyjny Newtona można zapisać, następująco:

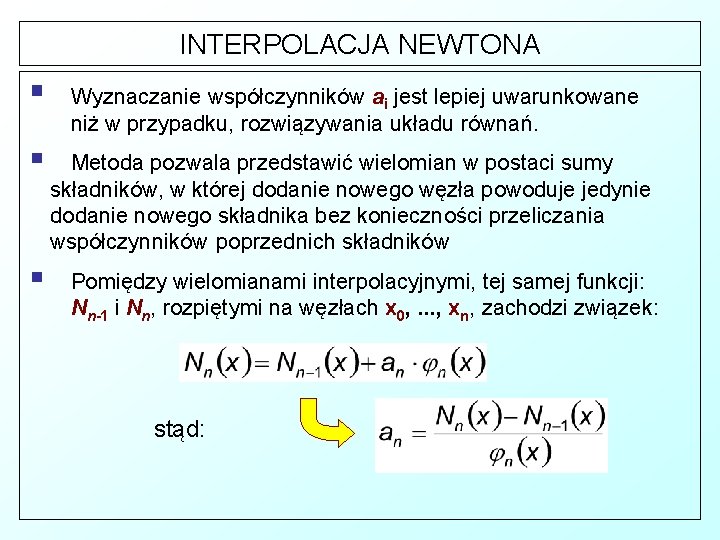
INTERPOLACJA NEWTONA § § § Wyznaczanie współczynników ai jest lepiej uwarunkowane niż w przypadku, rozwiązywania układu równań. Metoda pozwala przedstawić wielomian w postaci sumy składników, w której dodanie nowego węzła powoduje jedynie dodanie nowego składnika bez konieczności przeliczania współczynników poprzednich składników Pomiędzy wielomianami interpolacyjnymi, tej samej funkcji: Nn-1 i Nn, rozpiętymi na węzłach x 0, . . . , xn, zachodzi związek: stąd:

INTERPOLACJA NEWTONA § Współczynniki ai wielomianu interpolacyjnego Newtona zdefiniowane w powyższy sposób nazywane są ilorazami różnicowymi, które można przedstawić w następującej postaci: przy czym ilorazy pierwszego stopnia zdefiniowane są następująco: zaś wyższych stopni:

INTERPOLACJA NEWTONA § § Uogólniając postać przyrostową wielomianu na przypadek interpolacji N-punktowej uzyskujemy: Współczynniki wielomianu interpolacyjnego Newtona są następujące: .

INTERPOLACJA NEWTONA PRZYKŁAD: • Odtwarzanie ciągłego przebiegu temperatury otoczenia na podstawie nierównomiernej sekwencji pomiarów. • Stacja meteorologiczna dostarczyła pomiarów temperatury w postaci tabeli wartości: ð Rozwiązanie w postaci Lagrange’a (g – godzina jako ułamek dziesiętny): ð Rozwiązanie w postaci Newtona:

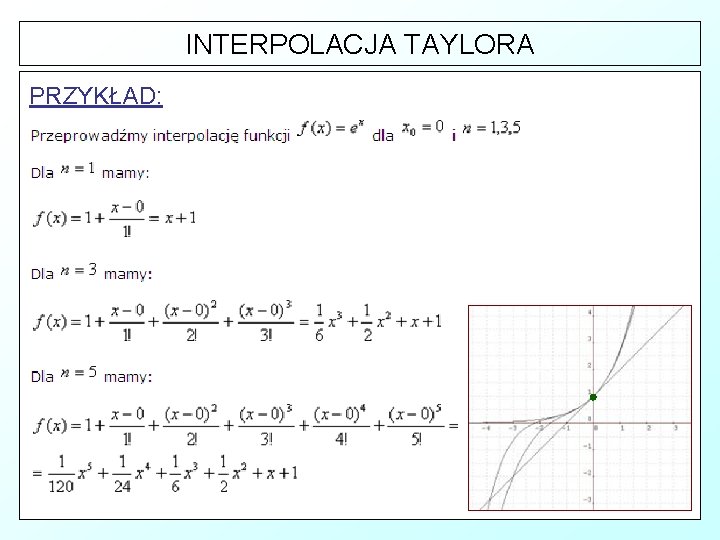
INTERPOLACJA TAYLORA ³ Interpolacji Taylora to prosta i popularna metoda do przybliżania funkcji w punkcie, mając dane wartości kolejnych pochodnych w tym punkcie. Ä Jeśli interpolowana funkcja f(x) jest określona w otoczeniu punktu x 0 i posiada n kolejnych pochodnych w tym otoczeniu, to możemy ją przybliżyć za pomocą wzoru Taylora: Ä Funkcja którą w ten sposób uzyskamy, w punkcie x 0 będzie miała równą wartość oraz równe n kolejnych pochodnych w stosunku do f(x).

INTERPOLACJA TAYLORA PRZYKŁAD:

INTERPOLACJA PADÉ ³ Interpolacji Padé jest odpowiednikiem interpolacji Taylora, zatem również zachowuje ona równość kolejnych pochodnych. Ä W tym przypadku jednak funkcją interpolującą jest funkcja wymierna postaci: Ä Ä Zbiór takich funkcji oznaczamy Rp, q , gdzie: • p oznacza stopień licznika, • q stopień mianownika i p m, q n. Gdy q = 0, to otrzymujemy wielomian interpolacyjny Taylora.

INTERPOLACJA PADÉ Ä Aby wyznaczyć współczynniki funkcji należy rozwiązań poniższy układ równań: gdzie: am występuje po prawej stronie p razy, a współczynniki 0, 1, . . . , p+q należą do rozwinięcia Maclaurina funkcji interpolowanej:

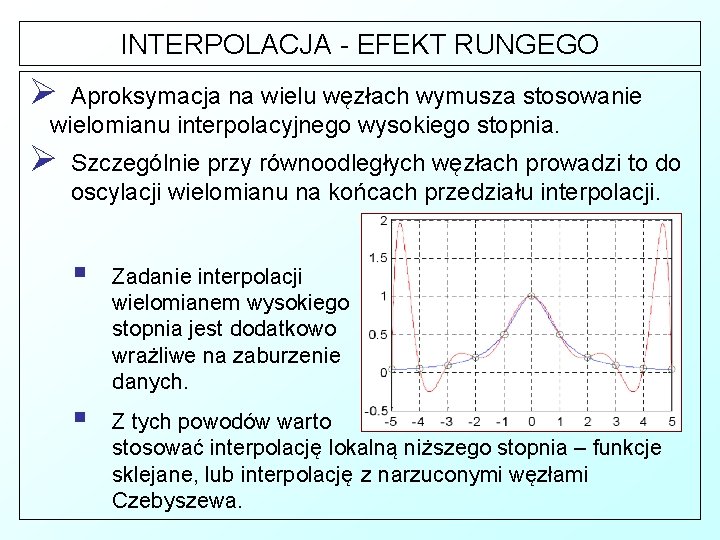
INTERPOLACJA - EFEKT RUNGEGO Ø Aproksymacja na wielu węzłach wymusza stosowanie wielomianu interpolacyjnego wysokiego stopnia. Ø Szczególnie przy równoodległych węzłach prowadzi to do oscylacji wielomianu na końcach przedziału interpolacji. § Zadanie interpolacji wielomianem wysokiego stopnia jest dodatkowo wrażliwe na zaburzenie danych. § Z tych powodów warto stosować interpolację lokalną niższego stopnia – funkcje sklejane, lub interpolację z narzuconymi węzłami Czebyszewa.

INTERPOLACJA FUNKCJAMI SKLEJANYMI ³ Szczególnie popularnym rodzajem interpolacji jest interpolacja funkcjami sklejanymi. ³ Główną cechą wyróżniającą ten rodzaj interpolacji, jest podział przedziału na którym znajdują się węzły, na mniejsze podprzedziały, a następnie użycie na każdym z nich wielomianu interpolacyjnego odpowiednio niskiego stopnia. ³ Wyznaczenie sklejanej funkcji interpolującej nie sprawia problemu (także, gdy węzłów jest bardzo dużo), tak jak późniejsze obliczanie jej wartości, co na pewno wpłynęło znacząco na jej popularność.

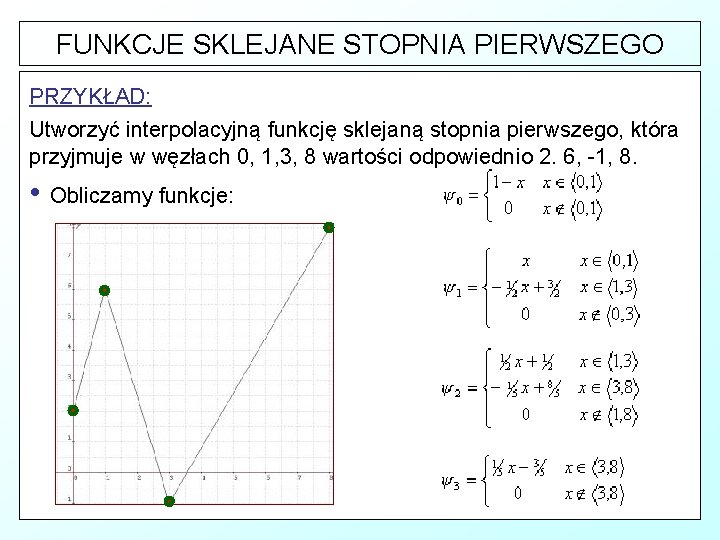
FUNKCJE SKLEJANE STOPNIA PIERWSZEGO § Funkcje sklejane stopnia pierwszego są najprostszym przypadkiem funkcji sklejanych. § Niech interpolowana funkcja przyjmuje w węzłach x 0 < x 1 < … < xn wartości odpowiednio y 0 < y 1 < … < yn. § Podstawą dla dalszych obliczeń będzie funkcja postaci: § Funkcja ta, w węźle xi przyjmuje wartość 1, w sąsiednich węzłach wartość 0, natomiast w każdym z przedziałów [xi-1, xi] , [xi, xi+1] jest funkcją liniową.

FUNKCJE SKLEJANE STOPNIA PIERWSZEGO PRZYKŁAD: Utworzyć interpolacyjną funkcję sklejaną stopnia pierwszego, która przyjmuje w węzłach 0, 1, 3, 8 wartości odpowiednio 2. 6, -1, 8. • Obliczamy funkcje:

FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z węzłami równoodległymi § Nakładając warunek równoodległości węzłów, otrzymujemy: § Określmy następnie funkcję bazową:

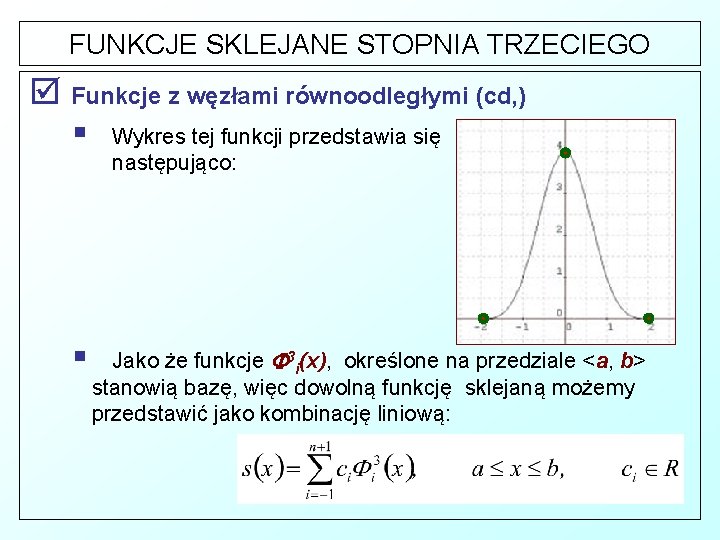
FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z węzłami równoodległymi (cd, ) § § Wykres tej funkcji przedstawia się następująco: Jako że funkcje 3 i(x), określone na przedziale <a, b> stanowią bazę, więc dowolną funkcję sklejaną możemy przedstawić jako kombinację liniową:

FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z węzłami równoodległymi (cd, ) § Aby wyznaczyć współczynniki ci , należy rozwiązać układ n+1 równań: wraz z jedną z trzech dodatkowych par warunków:

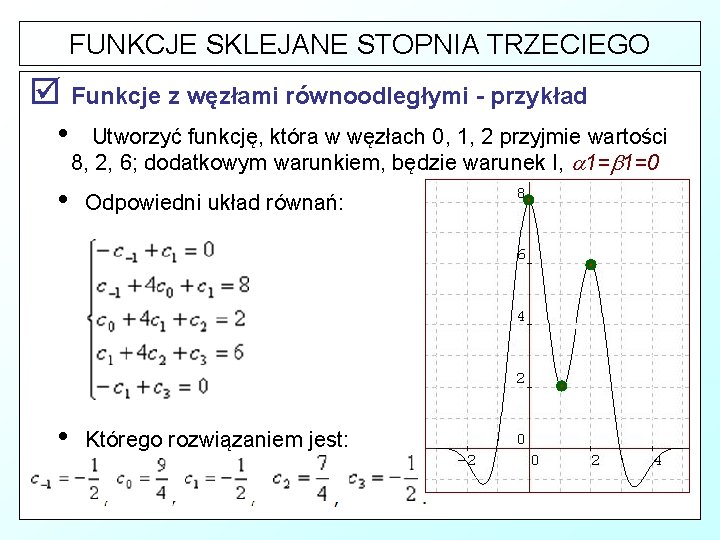
FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z węzłami równoodległymi - przykład • Utworzyć funkcję, która w węzłach 0, 1, 2 przyjmie wartości 8, 2, 6; dodatkowym warunkiem, będzie warunek I, 1= 1=0 • Odpowiedni układ równań: • Którego rozwiązaniem jest:

FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z dowolnymi węzłami § W przypadku węzłów dowolnych funkcje sklejaną na przedziale x < xj-1; xj> możemy przedstawić jako: gdzie:

FUNKCJE SKLEJANE STOPNIA TRZECIEGO þ Funkcje z dowolnymi węzłami (cd. ) § Dodatkowo spełniony musi być następujący układ równań:

FUNKCJE SKLEJANE STOPNIA TRZECIEGO : Warunki poprawnego sklejenia § § Niech będzie dana funkcja f : [a, b] R. § Funkcja sklejana S trzeciego stopnia dla funkcji f to funkcja S: R R C 2(R) spełniająca następujące warunki: Przedział [a, b] dzielimy na n podprzedziałów : a = x 0 < x 1 <. . . < xn = b i przyjmujemy, że w tych punktach (węzłach) znane są wartości funkcji f(xi) = yi. S jest wielomianem trzeciego stopnia na podprzedziale [xj , xj+1] dla każdego j = 0, 1, . . . , n − 1, S(xj) = f(xj) dla każdego j= 0, 1, . . . , n , Sj+1(xj+1) = fj(xj+1) dla każdego j = 0, 1, . . . , n − 2 , S’j+1(xj+1) = f’j(xj+1) dla każdego j = 0, 1, . . . , n − 2 ,

FUNKCJE SKLEJANE STOPNIA TRZECIEGO : Warunki poprawnego sklejenia (cd. ) § Funkcja sklejana S trzeciego stopnia dla funkcji f to funkcja S : R R C 2(R) spełniająca następujące warunki: S”j+1(xj+1) = S”j(xj+1) dla każdego j = 0, 1, . . . , n − 2 , jeden z poniższych warunków brzegowych jest spełniony: • S”(x 0) = S”(xn) = 0 (swobodne warunki brzegowe) • S’(x 0) = f’(x 0) i S’(xn) = f’(xn) (sztywne warunki brzegowe)

INTERPOLACJA W MATLABIE yi=interp 1(x, y, xi, ’metoda’) interpolacja funkcją jednej zmiennej xiy - wektory współrzędnych węzłów interpolacji xi - wektor punktów interpolacji Metoda: ‘linear’ - interpolacja funkcją łamana; ‘spline’ - interpolacja funkcjami sklejanymi trzeciego stopnia; ‘cubic’ - interpolacja wielomianami trzeciego stopnia

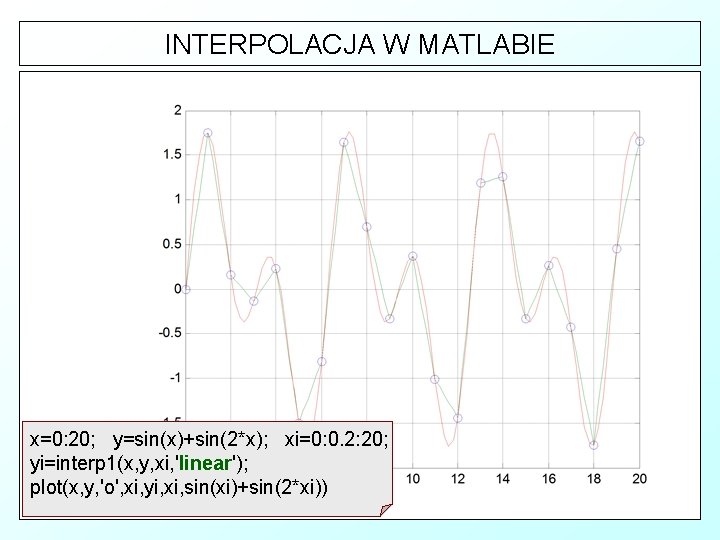
INTERPOLACJA W MATLABIE x=0: 20; y=sin(x)+sin(2*x); xi=0: 0. 2: 20; yi=interp 1(x, y, xi, 'linear'); plot(x, y, 'o', xi, yi, xi, sin(xi)+sin(2*xi))

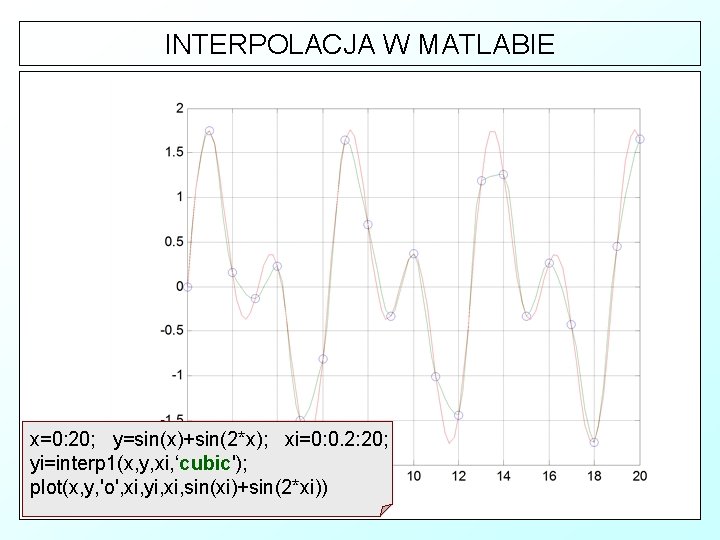
INTERPOLACJA W MATLABIE x=0: 20; y=sin(x)+sin(2*x); xi=0: 0. 2: 20; yi=interp 1(x, y, xi, ‘cubic'); plot(x, y, 'o', xi, yi, xi, sin(xi)+sin(2*xi))

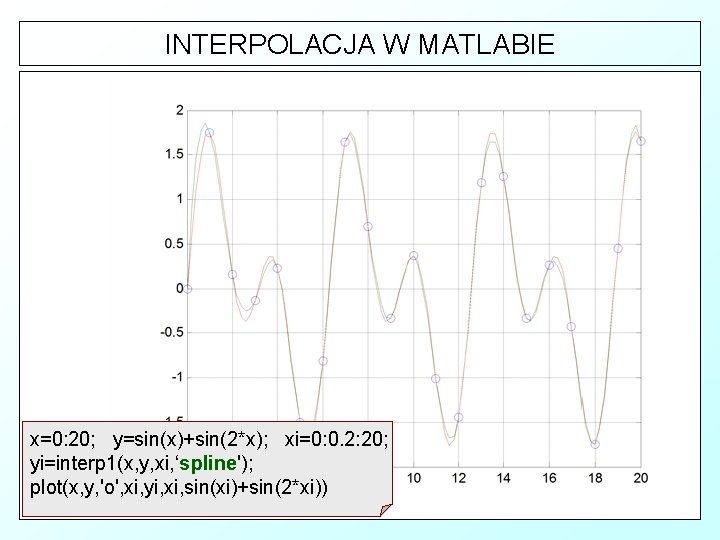
INTERPOLACJA W MATLABIE x=0: 20; y=sin(x)+sin(2*x); xi=0: 0. 2: 20; yi=interp 1(x, y, xi, ‘spline'); plot(x, y, 'o', xi, yi, xi, sin(xi)+sin(2*xi))