WYKAD 8 Cakowanie numeryczne Ryszard Myhan CAKA v

WYKŁAD 8 Całkowanie numeryczne Ryszard Myhan

CAŁKA v Całka jest jednym z najważniejszych pojęć współczesnej analizy matematycznej. v Zastosowania ma tak liczne, iż trudno je wymienić. v Stosuje się ją w matematyce, fizyce, technice i wielu innych dziedzinach nauki. v W matematyce badaniem własności i obliczaniem wartości całek zajmuje się dział zwany rachunkiem całkowym. v Za twórców tego rachunku uważa się dwóch wielkich matematyków Newtona oraz Leibniza, którzy opracowali teorię i metody związane z pojęciem całki.

CAŁKOWANIE NUMERYCZNE v Całkowanie numeryczne to przybliżone obliczanie całek oznaczonych. v Metody całkowania numerycznego polegają na przybliżeniu całki za pomocą odpowiedniej sumy ważonej wartości całkowanej funkcji w kilku punktach. Ø Aby uzyskać dokładniejsze przybliżenie dzieli się przedział całkowania na niewielkie fragmenty. Ø Ostateczny wynik jest sumą oszacowań całek w poszczególnych podprzedziałach. Ø Najczęściej przedział dzieli się na równe podprzedziały ale bardziej wyszukane algorytmy potrafią dostosowywać krok do szybkości zmienności funkcji.

METODY CAŁKOWANIA NUMERYCZNEGO v Można wyróżnić kilka metod całkowania numerycznego: ð metoda prostokątów ð metoda trapezów ð metoda Simpsona ð metody losowe

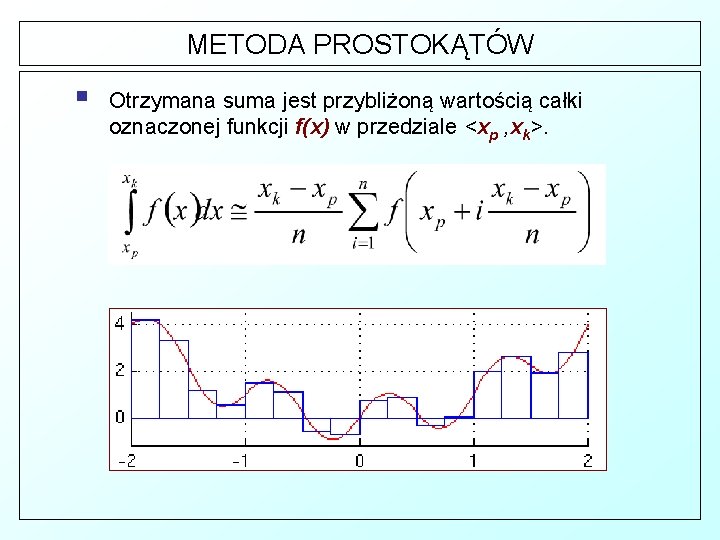
METODA PROSTOKĄTÓW t W metodzie prostokątów korzystamy z definicji całki oznaczonej Riemanna, w której wartość całki jest interpretowana jako suma pól obszarów pod wykresem krzywej w zadanym przedziale całkowania < xp, xk>. § § § Sumę tę przybliżamy przy pomocy sumy pól odpowiednio dobranych prostokątów. Przedział całkowania <xp, xk> dzielimy na n równo odległych punktów x 1, x 2, . . . , xn. Punkty te wyznaczamy wg wzoru:

METODA PROSTOKĄTÓW § Obliczamy odległość między dwoma sąsiednimi punktami (będzie to podstawa każdego prostokąta): § Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie: § Obliczamy sumę iloczynów wyznaczonych wartości funkcji przez odległość dx między dwoma sąsiednimi punktami (sumę pól poszczególnych prostokątów ograniczonych wykresem funkcji):

METODA PROSTOKĄTÓW § Otrzymana suma jest przybliżoną wartością całki oznaczonej funkcji f(x) w przedziale <xp , xk>.

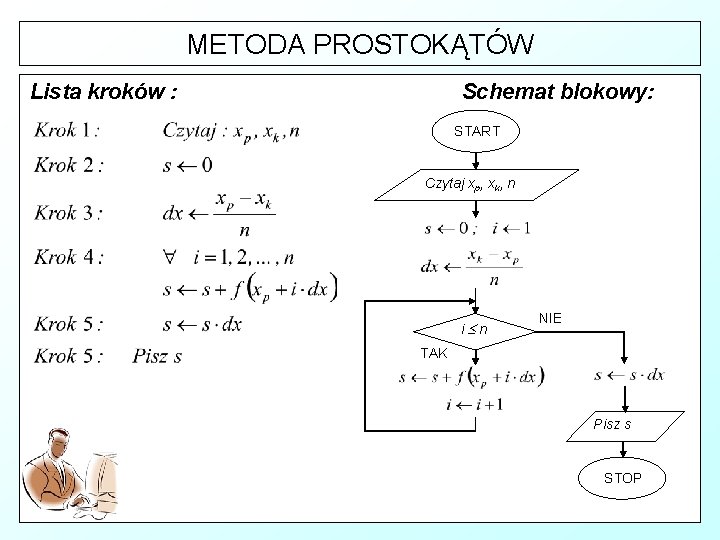
METODA PROSTOKĄTÓW Specyfikacja problemu. Dane wejściowe : xp - początek przedziału całkowania, xp R xk - koniec przedziału całkowania, xk R n - liczba punktów podziałowych, n N f(x) - funkcja rzeczywista, której całkę liczymy Dane wyjściowe : s - przybliżona wartość całki oznaczonej funkcji f(x) w przedziale <xp, xk>. s R Zmienne pomocnicze : dx - odległość między dwoma sąsiednimi punktami podziałowymi, dx R i - licznik punktów podziałowych, i N

METODA PROSTOKĄTÓW Lista kroków : Schemat blokowy: START Czytaj xp, xk, n i n NIE TAK Pisz s STOP

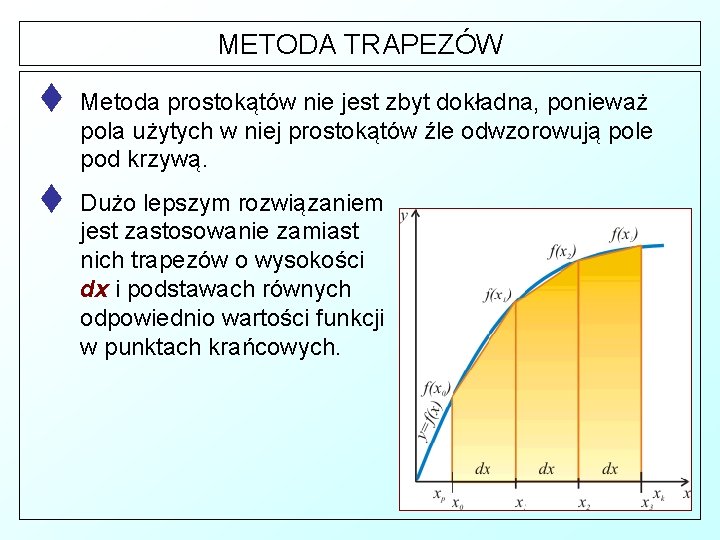
METODA TRAPEZÓW t Metoda prostokątów nie jest zbyt dokładna, ponieważ pola użytych w niej prostokątów źle odwzorowują pole pod krzywą. t Dużo lepszym rozwiązaniem jest zastosowanie zamiast nich trapezów o wysokości dx i podstawach równych odpowiednio wartości funkcji w punktach krańcowych.

METODA TRAPEZÓW t Sama zasada nie zmienia się: § § Przedział całkowania <xp, xk> dzielimy na n+1 równo odległych punktów x 0, x 1, x 2, . . . , xn. Punkty te wyznaczamy wg wzoru: § Obliczamy odległość między dwoma sąsiednimi punktami - będzie to wysokość każdego trapezu: § Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

METODA TRAPEZÓW § Pole pod wykresem funkcji przybliżane jest polami n trapezów, gdzie pole i-tego trapezu obliczamy wg wzoru: § Przybliżona wartość całki jest sumą pól wszystkich otrzymanych w ten sposób trapezów: czyli:

METODA TRAPEZÓW § Wyprowadzony na końcu wzór jest podstawą przybliżonego wyliczania całki w metodzie trapezów.

METODA TRAPEZÓW Specyfikacja problemu. Dane wejściowe : xp - początek przedziału całkowania, xp R xk - koniec przedziału całkowania, xk R n - liczba punktów podziałowych, n N f(x) - funkcja rzeczywista, której całkę liczymy Dane wyjściowe : Wartość całki oznaczonej funkcji f(x) w przedziale <xp, xk>. Zmienne pomocnicze : s - suma wysokości prostokątów, którą później zamieniamy w wartość całki, s R dx - odległość między dwoma sąsiednimi punktami podziałowymi, dx R i - licznik punktów podziałowych, i N

METODA TRAPEZÓW Lista kroków : Schemat blokowy: START Czytaj xp, xk, n NIE i n TAK Pisz s STOP

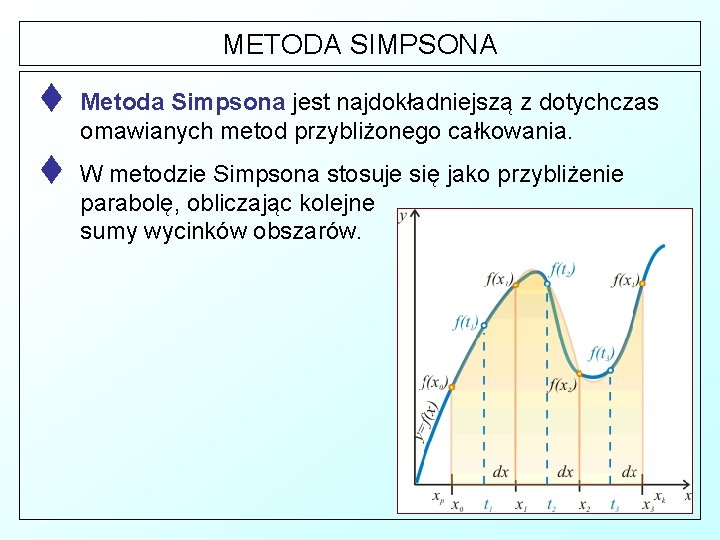
METODA SIMPSONA t Metoda Simpsona jest najdokładniejszą z dotychczas omawianych metod przybliżonego całkowania. t W metodzie Simpsona stosuje się jako przybliżenie parabolę, obliczając kolejne sumy wycinków obszarów.

METODA SIMPSONA t Zasada jest następująca: § Przedział całkowania <xp, xk> dzielimy na n+1 równo odległych punktów x 0, x 1, x 2, . . . , xn. § Dla każdych dwóch sąsiednich punktów wyznaczamy punkt środkowy ti wg wzoru: § Obliczamy odległość między dwoma sąsiednimi punktami.

METODA SIMPSONA § § Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie: • punkty podziałowe • punkty środkowe W każdym podprzedziale <xi-1, xi> przybliżamy funkcję za pomocą paraboli g(x) o następującej postaci:

METODA SIMPSONA § Parabola gi(x) musi przechodzić przez punkty: (xi-1, fi-1), (ti, fti), (xi, fi). § Współczynniki ai, bi i ci wyznacza się z układu trzech równań: § Pole pod parabolą w przedziale <xi-1, xi> będzie równe całce oznaczonej:

METODA SIMPSONA § Funkcja pierwotna to funkcja postaci: § Wartość całki dla i = 1, 2, . . . , n można obliczyć zgodnie z definicją Newtona-Leibniza:

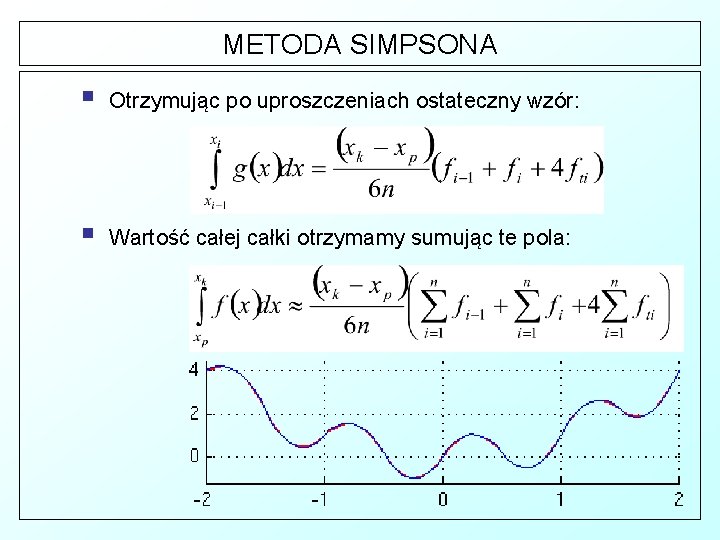
METODA SIMPSONA § Otrzymując po uproszczeniach ostateczny wzór: § Wartość całej całki otrzymamy sumując te pola:

METODA SIMPSONA § Ponieważ w obliczanych sumach wartości funkcji się powtarzają dwukrotnie (z wyjątkiem pierwszej i ostatniej), do obliczeń komputerowych stosuje się efektywniejszy wzór otrzymywania powyższej sumy:

METODA SIMPSONA Specyfikacja problemu. Dane wejściowe : xp - początek przedziału całkowania, xp R xk - koniec przedziału całkowania, xk R n - liczba punktów podziałowych, n N f(x) - funkcja rzeczywista, której całkę liczymy Dane wyjściowe : Wartość całki oznaczonej funkcji f(x) w przedziale <xp, xk>. Zmienne pomocnicze : s - suma wartości funkcji w punktach podziałowych, s R st - suma wartości funkcji w punktach podziałowych, st R dx - odległość między dwoma sąsiednimi punktami podziałowymi, dx R x - pozycja punktu podziałowego, x R i - licznik punktów podziałowych, i N

METODA SIMPSONA Lista kroków :

METODA SIMPSONA Schemat blokowy: START Czytaj xp, xk, n NIE TAK NIE i n i<n TAK Pisz s STOP

KWADRATURY ZŁOŻONE I ADAPTACYJNE i Przybliżanie funkcji o dużej zmienności na przedziale całkowania, za pomocą wielomianu interpolacyjnego może okazać się mało dokładne i z tego powodu dla takich funkcji stosuje się: ð kwadratury złożone ð kwadratury adaptacyjne

KWADRATURY ZŁOŻONE I ADAPTACYJNE 4 Kwadratura złożona sprowadza się do podzielenia przedziału <a, b> na pewną liczbę podprzedziałów i obliczenia całki na każdym z nich za pomocą wybranej kwadratury prostej, a następnie zsumowania tych wartości. 4 Kwadratura adaptacyjna polega na wstępnym podziale przedziału całkowania na dwa równe podprzedziały i obliczaniu całek w każdym z nich. Przedział, w którym nie osiągnięto wymaganej dokładności, jest ponownie dzielony na dwa podprzedziały równej długości i powtarzane jest całkowanie na każdym z nich, sprawdzanie dokładności i w razie potrzeby kolejny podział jednego lub obu podprzedziałów.

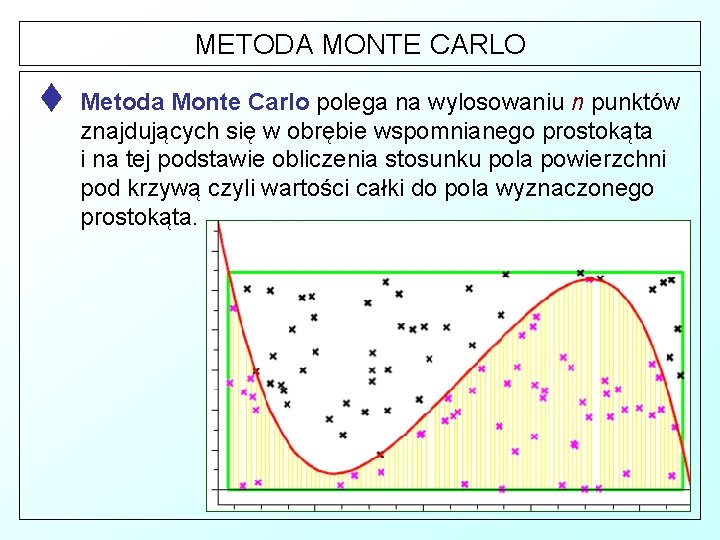
METODA MONTE CARLO t Załóżmy, że chcemy obliczyć całkę z funkcji f(x) w przedziale <xp; xk>. t Definicja całki oznaczonej Riemana, mówi, że wartość całki równa jest polu obszaru pod wykresem krzywej w zadanym przedziale całkowania. t Załóżmy, że wartości funkcji w obszarze całkowania mieszczą się w przedziale <yp; yk>. t Pole prostokąta wyznaczonego przez przedział całkowania: <xp; xk> oraz zakres wartości funkcji w tym przedziale: <yp; yk> jest prosty do wyznaczenia i wynosi:

METODA MONTE CARLO t Metoda Monte Carlo polega na wylosowaniu n punktów znajdujących się w obrębie wspomnianego prostokąta i na tej podstawie obliczenia stosunku pola powierzchni pod krzywą czyli wartości całki do pola wyznaczonego prostokąta.

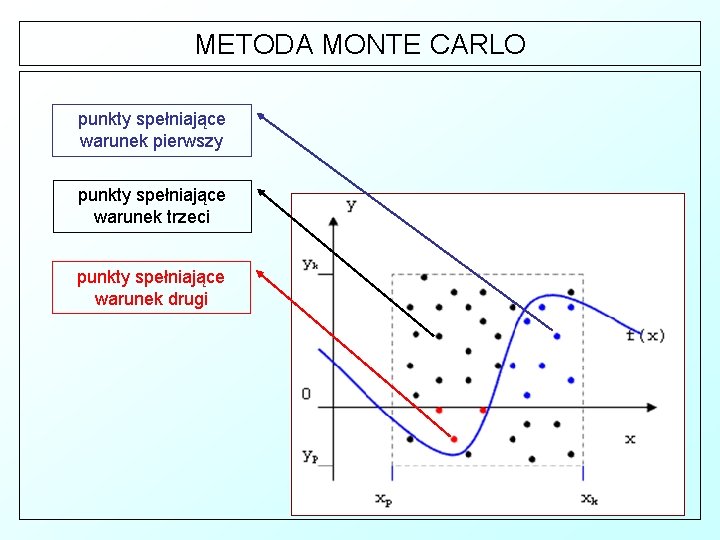
METODA MONTE CARLO t W tym celu wprowadza się zmienną pomocniczą c, której wartość modyfikuje się: § Jeżeli wylosowany punkt (xi , yi ) leży nad osią 0 X i jednocześnie pod wykresem funkcji całkowanej, czyli spełnia nierówność: 0 < yi ≤ f(xi), wówczas zwiększamy zmienną c o jeden, § Jeżeli wylosowany punkt (xi , yi ) leży pod osią 0 X i jednocześnie nad wykresem funkcji całkowanej, czyli spełnia nierówność: 0 > yi ≥ f(xi) , wówczas zmniejszamy zmienną c o jeden, § Jeżeli wylosowany punkt (xi , yi ) nie spełnia żadnego z powyższych warunków, wówczas pozostawiamy zmienną c bez zmian.

METODA MONTE CARLO punkty spełniające warunek pierwszy punkty spełniające warunek trzeci punkty spełniające warunek drugi

METODA MONTE CARLO : Na podstawie wylosowanych n punktów i przyporządkowania ich do odpowiedniej kategorii można wyznaczyć odpowiednie proporcje: : A po przekształceniach wartość szukanej całki można wyrazić wzorem: Wraz ze zwiększaniem się liczby punktów pomiarowych n, rozkładają się one coraz bardziej równomiernie w obrębie wyznaczonego prostokąta dając coraz dokładniejszy wynik.

METODA MONTE CARLO i Zaletą metody Monte Carlo jest łatwość jej zaprogramowania oraz (co chyba najważniejsze) fakt, że można ją bardzo łatwo zaadaptować do przypadku wielowymiarowego – zamiast par liczb trzeba będzie losować zestawy (n+1) liczb (liczba zmiennych funkcji podcałkowej plus jeden).

METODA MONTE CARLO Specyfikacja problemu. Dane wejściowe : xp - początek przedziału całkowania, xp R xk - koniec przedziału całkowania, xk R n - liczba punktów podziałowych, n N f(x) - funkcja rzeczywista, której całkę liczymy Dane wyjściowe : Wartość całki oznaczonej funkcji f(x) w przedziale <xp, xk>. Zmienne pomocnicze : s - średnia wartość funkcji, s R dx - długość przedziału całkowania, dx R x - punkt wybrany losowo z przedziału całkowania , x R i - licznik punktów podziałowych, i N

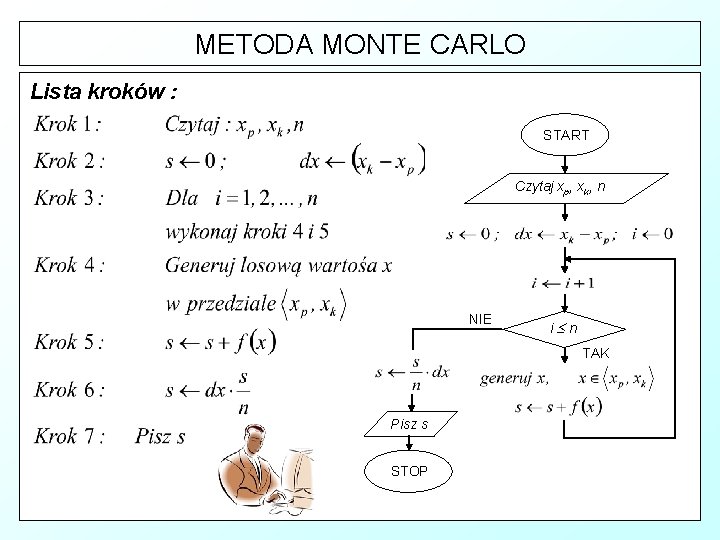
METODA MONTE CARLO Lista kroków : START Czytaj xp, xk, n NIE i n TAK Pisz s STOP