WYKAD 4 Sortowanie danych Ryszard Myhan SORTOWANIE DANYCH

WYKŁAD 4 Sortowanie danych Ryszard Myhan

SORTOWANIE DANYCH v Sortowanie danych jest jednym z podstawowych problemów programowania komputerów, z którym prędzej czy później spotka się każdy programista. Sortowanie jest wykorzystywane w bardzo wielu zastosowaniach: § § sport - wyniki uzyskane przez poszczególnych zawodników należy ułożyć w określonej kolejności, aby wyłonić zwycięzcę oraz podać lokatę każdego zawodnika. bank - spłaty kredytów należy ułożyć w odpowiedniej kolejności, aby wiadomo było kto i kiedy ma płacić odsetki do banku. grafika - wiele algorytmów graficznych wymaga porządkowania elementów, np. ścian obiektów ze względu na odległość od obserwatora. bazy danych - informacja przechowywana w bazie danych może wymagać różnego rodzaju uporządkowania, np. lista książek może być alfabetycznie porządkowana wg autorów lub tytułów, co znacznie ułatwia znalezienie określonej pozycji.

SORTOWANIE DANYCH Dane wejściowe: ciąg n liczb < a 1, a 2, . . . , an > Wyjście: permutacja < a’ 1, a’ 2, . . . , a’n > ciągu wejściowego taka, że a’ 1 a’ 2 . . . a’n t Jest bardzo wiele różnych algorytmów sortowania, a wszystkie różnią się znacznie czasem wykonywania i wymaganą pamięcią. t Jedne działają szybko dla każdego rodzaju danych, inne bardzo zwalniają dla pewnych typów danych wejściowych.

ALGORYTMY SORTUJĄCE v Algorytmy sortujące można podzielić się na: Algorytmy stabilne - zachowują kolejność elementów równych. § § Oznacza to, iż elementy o tych samych wartościach będą występowały w tej samej kolejności w zbiorze posortowanym, co w zbiorze nieposortowanym. Czasami ma to znaczenie, gdy sortujemy rekordy bazy danych i nie chcemy, aby rekordy o tym samym kluczu zmieniały względem siebie położenie. Algorytmy niestabilne - kolejność wynikowa elementów równych jest nieokreślona (zwykle nie zostaje zachowana).

ALGORYTMY SORTUJĄCE v Ze względu na złożoność pamięciową algorytmy sortujące dzieli się na dwie podstawowe grupy: Algorytmy sortujące w miejscu - wymagają stałej liczby dodatkowych struktur danych, niezależnej od liczby elementów sortowanego zbioru danych i ich wartości. § § Sortowanie odbywa się wewnątrz zbioru. Ma to istotne znaczenie przy dużych zbiorach danych, gdyż mogłoby się okazać, iż posortowanie ich nie jest możliwe z uwagi na brak pamięci w systemie. Algorytmy nie sortujące w miejscu – wymagają zarezerwowania w pamięci dodatkowych obszarów, których wielkość jest uzależniona od liczby sortowanych elementów lub od ich wartości. § Tego typu algorytmy są bardzo szybkie w działaniu, jednakże okupione to jest dodatkowymi wymaganiami na pamięć.

ALGORYTMY SORTUJĄCE v Każdy algorytm sortowania listy elementów opiera się na dwóch fundamentalnych zasadach: porównywaniu elementów w celu stwierdzenia, czy ich względna kolejność w liście jest zgodna z kryterium sortowania, przesuwaniu elementów na pozycje wyznaczane przez kryterium sortowania. Zalety i wady danego algorytmu sortowania wynikają przede wszystkim z tego, ile wymienionych wyżej operacji należy wykonać w celu posortowania określonego zbioru danych i jak efektywna jest każda z tych operacji.

SORTOWANIE ZWARIOWANE (Bogo Sort) & Jego działanie można scharakteryzować na przykładzie układania talii kart. Bierzemy talię kart i sprawdzamy czy jest ułożona - jeśli nie, tasujemy ją i znów sprawdzamy ułożenie. Operacje sprawdzania i tasowania wykonujemy dotąd, aż talia nam się ułoży w pożądanej kolejności Algorytm opiera się na losowym sortowaniu zbioru. Ten sam zbiór raz może zostać błyskawicznie posortowany (gdy akurat mamy szczęście) a innym razem możemy czekać na wynik nawet cały rok (albo jeszcze dłużej). Sortowanie odbywa się w miejscu. Jest to jeden z najgorszych algorytmów sortujących, gdyż posiada pesymistyczną (superwykładniczą) czasową złożoność obliczeniową klasy Q(n x n!).

SORTOWANIE ZWARIOWANE (Bogo Sort) Specyfikacja algorytmu: § Dane wejściowe: n - liczba elementów w sortowanym zbiorze, n N d[ ] - zbiór n-elementowy, który będzie sortowany. Elementy zbioru mają indeksy od 1 do n. § Dane wyjściowe: d[ ] - posortowany zbiór n-elementowy. Elementy zbioru mają indeksy od 1 do n. § Zmienne pomocnicze: i - zmienna sterująca pętli, i N i 1, i 2 - losowe indeksy elementów zbioru d[ ], i 1, i 2 N

SORTOWANIE ZWARIOWANE (Bogo Sort) Lista kroków: @ Algorytm główny • • Krok 1 : Dopóki Posortowane = false to Tasuj Krok 1 : Zakończ algorytm. @ Algorytm funkcji Posortowane • • Krok 1 : Dla i = 1, 2, . . . , n - 1, jeśli d[i] > d[i + 1], to Posortowane : = false i zakończ algorytm Krok 2 : Posortowane : = true i zakończ algorytm @ Algorytm procedury Tasuj • • Krok 1 : Dla i = (1, 2, . . . , 3) * n, wykonuj kroki 2 i 3 Krok 2 : Wylosuj indeksy i 1 i i 2 w przedziale od 1 do n Krok 3 : Wymień zawartości d [i 1] d [i 2] Krok 4 : Zakończ algorytm

SORTOWANIE ZWARIOWANE (Bogo Sort) Schemat blokowy: Algorytm główny START Algorytm funkcji Posortowane Algorytm procedury Tasuj START i=1 TAK posortowane NIE i<n posortowane=True i<=3 NIE TAK Tasuj TAK losuj indeksy i 1 oraz i 2 z przedziału <1, n> d[i]=d[i=1] NIE STOP NIE posortowane=False d[i] d[i+1] i=i+1 STOP

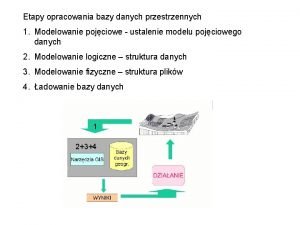
SORTOWANIE NAIWNE & Sortowanie naiwne jest również bardzo złym algorytmem sortującym, lecz, w przeciwieństwie do sortowania zwariowanego, daje zawsze poprawne wyniki. Przeglądane są kolejne pary sąsiednich elementów zbioru. Jeśli bieżąco przeglądana para elementów jest w złej kolejności, elementy pary zamieniane są miejscami. Naiwność algorytmu wyraża się tym, iż po napotkaniu nieposortowanych elementów algorytm zamienia je miejscami, a następnie rozpoczyna całą pracę od początku zbioru. Złożoność obliczeniowa algorytmu przy sortowaniu zbioru nieuporządkowanego ma klasę Q(n 3). Sortowanie odbywa się w miejscu.

SORTOWANIE NAIWNE Schemat blokowy: • W pętli sprawdzamy kolejność elementu d[i] z elementem następnym d[i+1]. START i : = 1 d[i] d[i+1] d[i] > d[i+1] NIE i : = i + 1 NIE i=n TAK STOP • Rozpoczynamy przeglądanie zbioru od pierwszego elementu (i = 1). TAK • Jeżeli założyliśmy porządek rosnący, to gdy d[i] > d[i+1] elementy te są w złej kolejności. • W takiej sytuacji zamieniamy je miejscami, a indeks i ustawiamy z powrotem na 1 i wracamy na początek pętli. • Jeśli elementy są w dobrej kolejności, zwiększamy indeks i o 1, sprawdzamy, czy osiągnął już wartość końcową n i jeśli nie, wracamy na początek pętli. • W przeciwnym razie kończymy - zbiór jest posortowany.

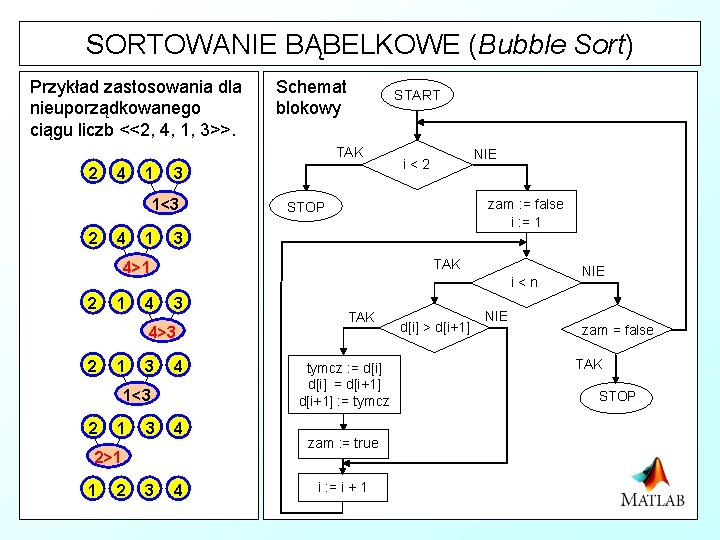
SORTOWANIE BĄBELKOWE (Bubble Sort) & Jest to jeden z prostszych algorytmów sortowania. Algorytm nosi nazwę bąbelkowego, gdyż najmniejsze liczby "wypływają" z dołu tablicy na jej szczyt. Sprawdzamy całą tablicę od końca, jeżeli trafimy na parę elementów, w której większy poprzedza mniejszy to zamieniamy je miejscami i znów zaczynamy przeszukiwać tablicę od końca. Czynność powtarzamy tak długo aż podczas sprawdzania całej tablicy, nie zajdzie ani jedna zamiana elementów. Algorytm sortowania bąbelkowego przy porządkowaniu zbioru nieposortowanego ma klasę czasowej złożoności obliczeniowej równą Q(n 2). Sortowanie odbywa się w miejscu.

SORTOWANIE BĄBELKOWE (Bubble Sort) Przykład zastosowania dla nieuporządkowanego ciągu liczb <<2, 4, 1, 3>>. Schemat blokowy START TAK 2 4 1 3 1<3 2 4 1 zam : = false i : = 1 STOP 3 TAK 4>1 2 1 4 i<n 3 4>3 2 1 3 4 1<3 2 1 3 4 2>1 1 2 NIE i<2 TAK tymcz : = d[i] = d[i+1] : = tymcz zam : = true i : = i + 1 d[i] > d[i+1] NIE zam = false TAK STOP

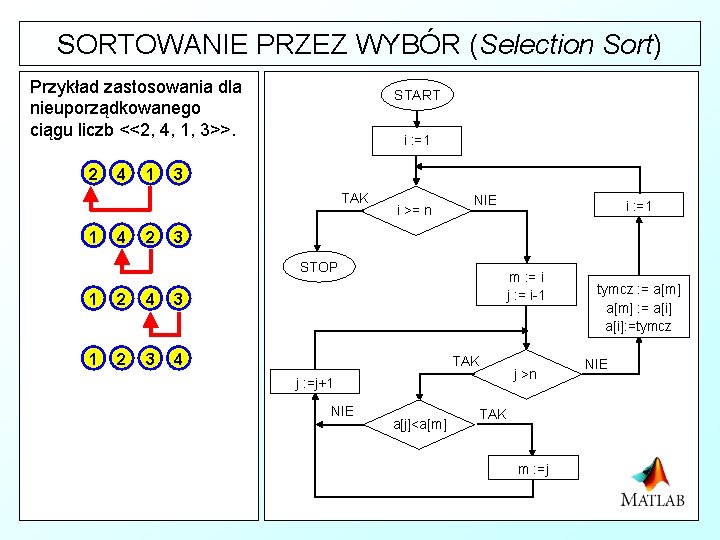
SORTOWANIE PRZEZ WYBÓR (Selection Sort) & Idea algorytmu sortowania przez wybór zakłada, że jeżeli chcemy posortować zbiór liczbowy rosnąco, to element najmniejszy powinien znaleźć się na pierwszej pozycji. Na początku szukany jest najmniejszy element, po znalezieniu go jest on zamieniany z pierwszym elementem tablicy. Następnie szukany jest znów najmniejszy element, ale począwszy od elementu drugiego (pierwszy - najmniejszy jest już wstawiony na odpowiednie miejsce), po jego znalezieniu jest on zamieniany z drugim elementem. Czynność tą powtarzamy kolejno na elementach od trzeciego, czwartego, aż do n-tego Algorytm sortowania przez wybór posiada klasę czasowej złożoności obliczeniowej równą Q(n 2). Sortowanie odbywa się w miejscu.

SORTOWANIE PRZEZ WYBÓR (Selection Sort) Przykład zastosowania dla nieuporządkowanego ciągu liczb <<2, 4, 1, 3>>. 2 4 1 START i : =1 3 TAK 1 4 2 i >= n NIE i : =1 3 STOP 1 2 4 3 1 2 3 4 m : = i j : = i-1 TAK j >n j : =j+1 NIE a[j]<a[m] TAK m : =j tymcz : = a[m] : = a[i]: =tymcz NIE

SORTOWANIE PRZEZ WSTAWIANIE (Insert Sort) & Zasada działania tego algorytmu jest często porównywana do porządkowania kart w wachlarz podczas gry. Każdą kartę wstawiamy w odpowiednie miejsce, tzn. po młodszej, ale przed starszą. Algorytm składał się z dwóch pętli: Pętla główna symuluje pobieranie elementów zbioru. Pętla sortująca (wewnętrzna) szuka dla pobranego elementu miejsca na liście uporządkowanej. Jeśli takie miejsce zostanie znalezione, to elementy listy są rozsuwane, aby tworzyć miejsce na nowy element. Jeśli na liście uporządkowanej nie ma elementu większego od wybranego, to element ten trafia na koniec listy. § Algorytm ma klasę czasowej złożoności obliczeniowej Q(n 2). § Sortowanie odbywa się w miejscu.

SORTOWANIE PRZEZ WSTAWIANIE (Insert Sort) Przykład zastosowania dla nieuporządkowanego ciągu liczb <<2, 4, 1, 3>>. 2 4 1 START i=n-1 3 NIE TAK i>=0 tymcz=a[1] j=j+1 2 2 1 1 4 2 2 TAK tymcz>a[j] 4 3 j<=n NIE TAK a[j-1]=a[j] j=j+1 4 STOP a[j-1]=tymcz i=i-1

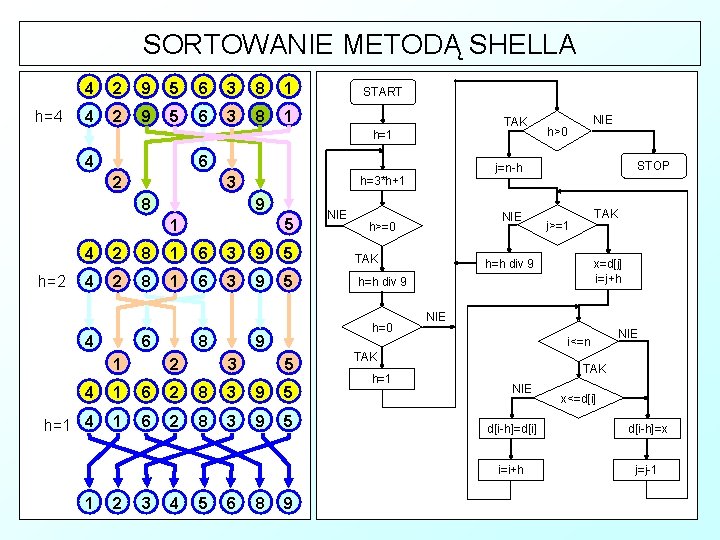
SORTOWANIE METODĄ SHELLA & W latach 50 -tych XX wieku informatyk Donald Shell zauważył, iż algorytm sortowania przez wstawianie pracuje bardzo efektywnie w przypadku gdy zbiór jest w dużym stopniu uporządkowany, a gdy zbiór jest nieuporządkowany to algorytm ten pracuje nieefektywnie. Pomysł Shella polegał na tym, że sortowany zbiór dzielimy na podzbiory, których elementy są odległe od siebie w sortowanym zbiorze o pewien odstęp h. Każdy z tych podzbiorów sortujemy algorytmem przez wstawianie a następnie zmniejszamy odstęp - powoduje to powstanie nowych podzbiorów (będzie ich już mniej). Sortowanie powtarzamy i znów zmniejszamy odstęp, aż osiągnie on wartość 1 - wtedy sortujemy już normalnie za pomocą Instertion Sort.

SORTOWANIE METODĄ SHELLA h=4 4 2 9 5 6 3 8 1 START TAK h=1 6 4 3 2 5 1 h=2 NIE 2 8 1 6 3 9 5 TAK 4 2 8 1 6 3 9 5 h=h div 9 4 6 1 8 2 h=0 9 3 5 1 6 2 8 3 9 5 h=1 4 1 6 2 8 3 9 5 2 3 4 5 6 8 STOP TAK j>=1 h=h div 9 x=d[j] i=j+h NIE i<=n 4 1 NIE h>=0 4 h>0 j=n-h h=3*h+1 9 8 NIE 9 TAK h=1 NIE TAK NIE x<=d[i] d[i-h]=x i=i+h j=j-1

SORTOWANIE SZYBKIE (Quick Sort) & Sortowanie szybkie zostało wynalezione przez angielskiego informatyka, profesora Tony'ego Hoare'a w latach 60 -tych ubiegłego wieku. Algorytm sortowania szybkiego jest uważany za najszybszy algorytm dla danych losowych. Zasada jego działania opiera się o metodę dziel i zwyciężaj. Zbiór danych zostaje podzielony na dwa podzbiory i każdy z nich jest sortowany niezależnie od drugiego Dla zadanej tablicy a[l. . p] wybieramy element v=a[l] i przeszukujemy resztę tablicy (tzn. a[l+1. . p]) tak długo, aż nie znajdziemy elementu nie większego niż a[l]. Następnie przeszukujemy tę tablicę od strony prawej póki nie znajdziemy elementu nie większego niż a[l].

SORTOWANIE SZYBKIE (Quick Sort) Gdy to osiągniemy, zamieniamy miejscami te dwa elementy i zaczynamy cały proces od początku. Algorytm działa tak długo, aż wskaźnik poruszający się w lewo i wskaźnik poruszający się w prawo spotkają się - należy wówczas zamienić element v=a[l] z ostatnim elementem lewej części. Mimo, że w najgorszym przypadku algorytm ma złożoność kwadratową, jest on bardzo często stosowany. Powodem tego jest niska- liniowologarytmiczna, złożoność w średnim przypadku.

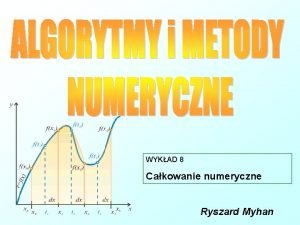
SORTOWANIE SZYBKIE (Quick Sort) Specyfikacja algorytmu. Dane wejściowe : d[] - zbiór zawierający elementy do posortowania. lewy - indeks pierwszego elementu w zbiorze, lewy C prawy - indeks ostatniego elementu w zbiorze, prawy C Dane wyjściowe : d[] - zbiór zawierający elementy posortowane Zmienne pomocnicze : pivot - element podziałowy i, j - indeksy elementów, i, j C

SORTOWANIE SZYBKIE (Quick Sort) Lista kroków : Krok 1 : i : = (lewy + prawy) / 2; Krok 2 : piwot : = d[i]; d[i] : = d[prawy]; j : = lewy Krok 3 : Dla i = lewy, lewy + 1, . . . , prawy - 1: wykonuj kroki 4. . . 5 Krok 4 : Krok 5 : Krok 6 : Krok 7 : Jeśli d[i] >= piwot, to wykonaj kolejny obieg pętli z kroku 3 d[i] « d[j]; j : = j + 1 d[prawy] : = d[j]; d[j] : = piwot; Jeśli lewy < j - 1, to wykonaj rekurencyjnie Sortuj_szybko(lewy, j - 1) Krok 8 : Jeśli j + 1 < prawy, to wykonaj rekurencyjnie Sortuj_szybko(j + 1, prawy) Krok 9 : Zakończ algorytm

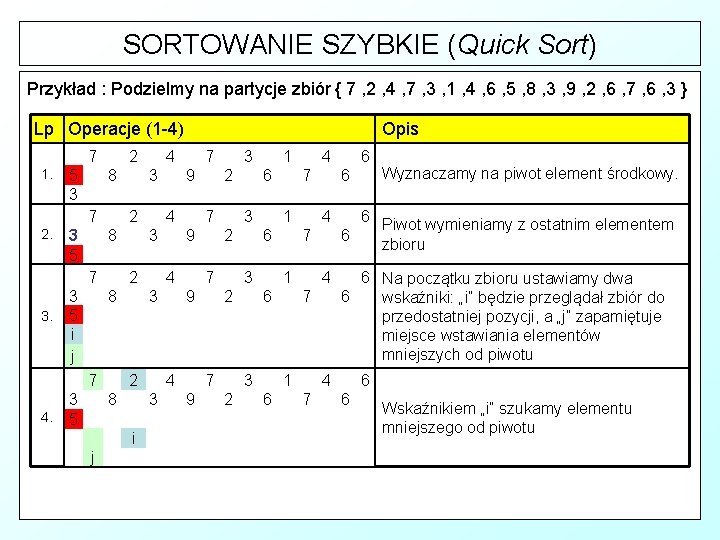
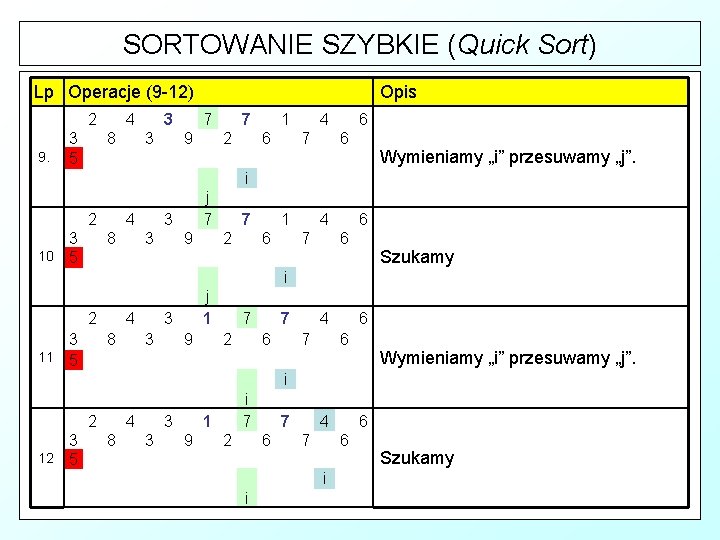
SORTOWANIE SZYBKIE (Quick Sort) Przykład : Podzielmy na partycje zbiór { 7 , 2 , 4 , 7 , 3 , 1 , 4 , 6 , 5 , 8 , 3 , 9 , 2 , 6 , 7 , 6 , 3 } Lp Operacje (1 -4) 7 1. 5 3 2 8 7 2. 3 5 2 7 3 3. 5 i j 6 6 4 7 1 6 6 7 6 6 4 1 3 2 7 6 2 4 1 3 7 9 6 2 9 1 3 7 4 3 i 7 4 2 3 2 9 3 8 j 4 2 7 7 9 3 8 3 4. 5 4 3 8 Opis Piwot wymieniamy z ostatnim elementem zbioru 6 Na początku zbioru ustawiamy dwa 6 wskaźniki: „i” będzie przeglądał zbiór do przedostatniej pozycji, a „j” zapamiętuje miejsce wstawiania elementów mniejszych od piwotu 4 7 Wyznaczamy na piwot element środkowy. 6 6 Wskaźnikiem „i” szukamy elementu mniejszego od piwotu

SORTOWANIE SZYBKIE (Quick Sort) Lp Operacje (5 -8) 2 3 5. 5 7 8 3 6. 5 4 3 i j 7 2 8 Opis 7 9 4 3 3 2 7 9 1 6 3 2 4 7 1 6 6 6 4 7 Znaleziony element wymieniamy z elementem na pozycji j-tej. Po wymianie wskaźnik j przesuwamy o 1 pozycję. 6 6 Szukamy i j 4 2 3 7. 5 8 2 3 8. 5 7 3 9 i j 7 4 8 7 3 3 2 7 9 6 3 2 4 7 1 6 i j 1 6 6 4 7 Wymieniamy „i” przesuwamy „j”. 6 6 Szukamy

SORTOWANIE SZYBKIE (Quick Sort) Lp Operacje (9 -12) 2 9. 3 5 4 8 3 3 Opis 7 9 7 2 1 6 4 7 6 6 Wymieniamy „i” przesuwamy „j”. i 2 3 10 5 4 8 j 7 3 3 9 7 2 1 6 4 7 6 6 Szukamy i 2 3 11 5 4 8 j 1 3 3 9 7 2 7 6 4 7 6 6 Wymieniamy „i” przesuwamy „j”. i 2 3 12 5 4 8 3 3 i 7 1 9 2 7 6 4 7 6 i i 6 Szukamy

SORTOWANIE SZYBKIE (Quick Sort) Lp Operacje (13 -16) 2 3 13 5 4 8 3 3 Opis 1 9 4 2 7 6 7 7 6 6 Wymieniamy „i” przesuwamy „j”. i 2 3 14 5 i 4 8 2 7 15 5 i 3 4 8 2 7 16 5 i 3 9 3 3 4 8 1 1 3 3 4 2 9 6 2 7 6 4 2 7 j 3 4 1 9 j 7 6 7 7 Szukamy 6 6 j 7 3 6 6 7 6 6 j Wymieniamy „i” przesuwamy „j”. Szukamy

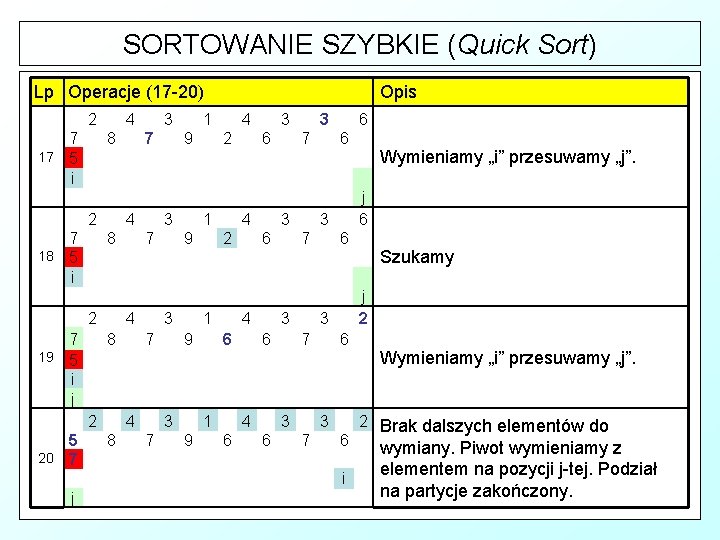
SORTOWANIE SZYBKIE (Quick Sort) Lp Operacje (17 -20) 2 7 17 5 i 4 8 2 7 18 5 i 4 2 6 7 6 6 i j Szukamy j 2 3 7 Wymieniamy „i” przesuwamy „j”. j 6 3 3 6 6 7 6 6 3 3 4 1 9 6 2 9 3 4 1 3 7 2 9 7 4 1 3 4 8 9 7 8 1 3 4 2 5 20 7 7 8 7 19 5 i j 3 Opis Wymieniamy „i” przesuwamy „j”. 2 Brak dalszych elementów do wymiany. Piwot wymieniamy z elementem na pozycji j-tej. Podział na partycje zakończony.

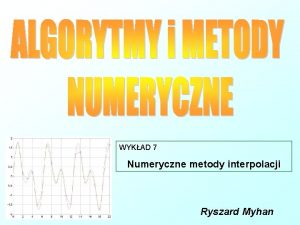
SORTOWANIE SZYBKIE (Quick Sort) START d[prawy]=d[j]=prawy i=(lewy+prawy)/2 pivot=d[i]=d[prawy] j=lewy i=lewy NIE lewy<j-1 TAK i<prawy i=i+1 NIE Sortuj_szybko (lewy, j-1) TAK NIE d[i]<pivot j+1<prawy NIE TAK d[i] d[j] TAK Sortuj_szybko (j+1, prawy) STOP

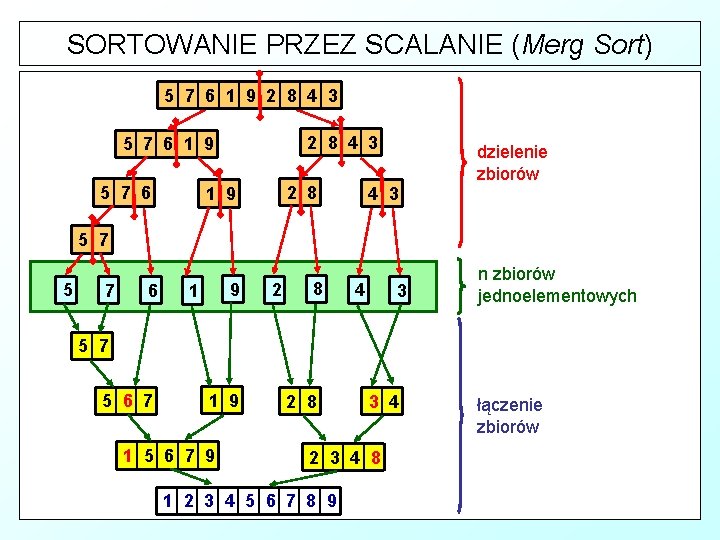
SORTOWANIE PRZEZ SCALANIE (Merg Sort) & Wynaleziony w 1945 roku przez Johna von Neumanna algorytm sortowania przez scalanie jest algorytmem rekurencyjnym. Wykorzystuje zasadę dziel i zwyciężaj, która polega na podziale zadania głównego na zadania mniejsze dotąd, aż rozwiązanie stanie się oczywiste. Algorytm sortujący dzieli porządkowany zbiór na kolejne połowy dopóki taki podział jest możliwy (tzn. podzbiór zawiera co najmniej dwa elementy). Następnie uzyskane w ten sposób części zbioru rekurencyjnie sortuje się tym samym algorytmem. Posortowane części łączy się ze sobą za pomocą scalania tak, aby wynikowy zbiór był posortowany.

SORTOWANIE PRZEZ SCALANIE (Merg Sort) Podstawową operacją algorytmu jest scalanie dwóch zbiorów uporządkowanych w jeden zbiór również uporządkowany. Operację scalania realizuje się wykorzystując pomocniczy zbiór, w którym tymczasowo odkładane są scalane elementy dwóch zbiorów. Ogólna zasada jest następująca: Przygotuj pusty zbiór tymczasowy Dopóki żaden ze scalanych zbiorów nie jest pusty, porównuj ze sobą pierwsze elementy każdego z nich i w zbiorze tymczasowym umieszczaj mniejszy z elementów usuwając go ze scalanego zbioru. W zbiorze tymczasowym umieść zawartość tego scalanego zbioru, który zawiera jeszcze elementy. Zawartość zbioru tymczasowego przepisz do zbioru wynikowego i zakończ algorytm.

SORTOWANIE PRZEZ SCALANIE (Merg Sort) 5 7 6 1 9 2 8 4 3 5 7 6 1 9 5 7 6 2 8 1 9 4 3 dzielenie zbiorów 5 7 6 9 1 2 8 4 3 n zbiorów jednoelementowych 5 7 5 6 7 1 9 1 5 6 7 9 2 8 3 4 2 3 4 8 1 2 3 4 5 6 7 8 9 łączenie zbiorów

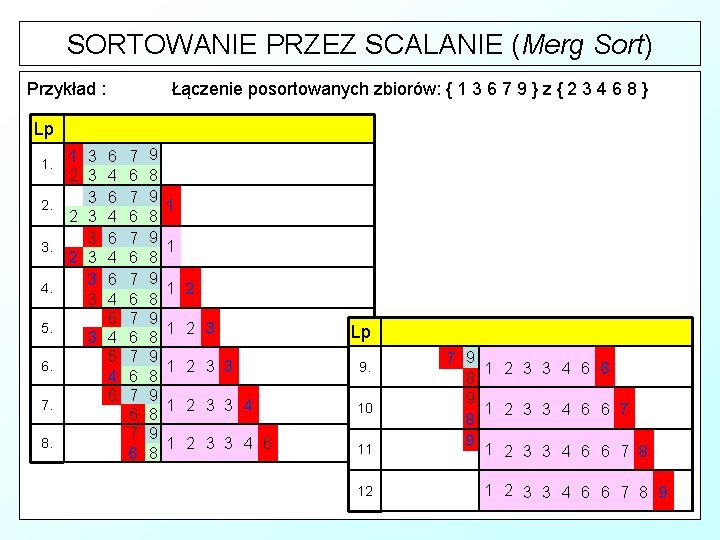
SORTOWANIE PRZEZ SCALANIE (Merg Sort) Przykład : Łączenie posortowanych zbiorów: { 1 3 6 7 9 } z { 2 3 4 6 8 } Lp 1. 2. 3. 4. 5. 6. 7. 8. 1 3 6 2 3 4 3 6 3 4 6 4 6 7 6 7 6 9 8 9 8 1 1 1 2 3 Lp 1 2 3 3 9. 1 2 3 3 4 10 1 2 3 3 4 6 11 12 7 9 1 2 3 3 4 6 6 8 9 1 2 3 3 4 6 6 7 8 9

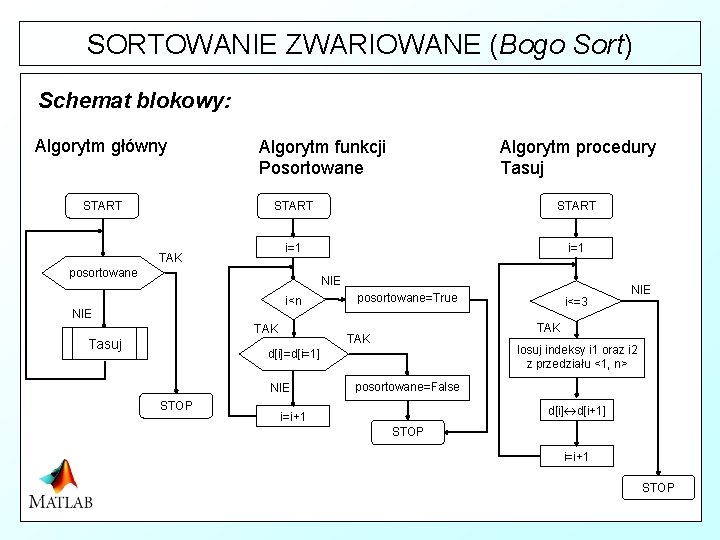
SORTOWANIE PRZEZ SCALANIE (Merg Sort) Specyfikacja algorytmu. Dane wejściowe : d[] - zbiór scalany ip - indeks pierwszego elementu w młodszym podzbiorze, is - indeks pierwszego elementu w starszym podzbiorze, Ik - indeks ostatniego elementu w starszym podzbiorze, Dane wyjściowe : d[] - zbiór scalany Zmienne pomocnicze : p [ ] - zbiór pomocniczy zawierający elementów co zbiór d i 1 - indeks elementów w młodszej połówce zbioru d[ ], i 2 - indeks elementów w starszej połówce zbioru d[ ], i - indeks elementów w zbiorze p[ ],

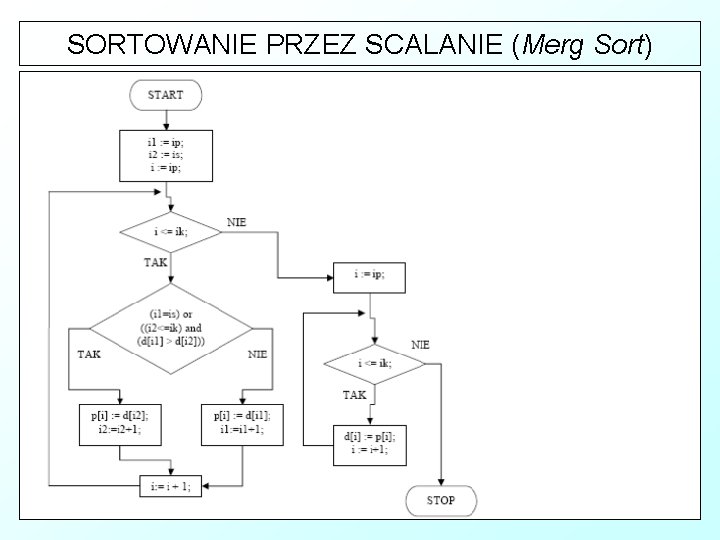
SORTOWANIE PRZEZ SCALANIE (Merg Sort) Lista kroków : Krok 1 : i 1 : = ip; i 2 : = is; i : = ip; Krok 2 : Dla i: = ip , ip + 1, . . . . ik wykonaj : Jeśli (i 1 = is) or ((i 2 <= ik) and (d[i 1] > d[i 2])) to p[i] : = d[i 2] ; i 2: = i 2 + 1; w przeciwnym przypadku p[i] : = d[i 1] ; i 1: = i 1 + 1; Krok 3 : Dla i: = ip , ip + 1, . . . . ik wykonaj : d[i] : = p[i]; Krok 4 : Zakończ algorytm

SORTOWANIE PRZEZ SCALANIE (Merg Sort)

SORTOWANIE PRZEZ ZLICZANIE (Counting Sort) & Sortowanie przez zliczanie – metoda sortowania danych, która polega na sprawdzeniu ile wystąpień kluczy mniejszych od danego występuje w sortowanej tablicy. Algorytm zakłada, że klucze elementów należą do skończonego zbioru (np. są to liczby całkowite z przedziału 0. . 100), co ogranicza możliwości jego zastosowania. Algorytm sortujący dzieli porządkowany zbiór na kolejne połowy dopóki taki podział jest możliwy (tzn. podzbiór zawiera co najmniej dwa elementy). Następnie uzyskane w ten sposób części zbioru rekurencyjnie sortuje tym samym algorytmem. Posortowane części łączy ze sobą za pomocą scalania tak, aby wynikowy zbiór był posortowany.

SORTOWANIE PRZEZ ZLICZANIE (Counting Sort) Przykład: Posortować rosnąco zbiór danych: { 6; 3; 6; 1; 4; 9; 0; 1; 8; 2; 6; 4; 9; 3; 7; 5; 9; 2; 7; 3; 2; 4; 1; 8; 7; 0; 8; 5; 8; 3; 6; 2; 5; 3 } § Przeglądamy zbiór i wypisujemy wszystkie wartości w zbiorze: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 § Przeglądamy kolejne elementy zbioru i zliczamy ich wystąpienia w odpowiednich licznikach: [0: 2] [1: 3] [2: 4] [3: 5] [4: 3] [5: 3] [6: 4] [7: 3] [8: 4] [9: 3] § Następnie, poczynając od drugiego licznika sumujemy zawartość licznika oraz jego poprzedników [0: 2] [1: 5] [2: 9] [3: 14] [4: 17] [5: 20] [6: 24] [7: 27] [8: 31] [9: 34] § Stan licznika określa ostatnią pozycję w zbiorze, na której należy umieścić wartość równą numerowi licznika:

SORTOWANIE PRZEZ ZLICZANIE (Counting Sort) Specyfikacja algorytmu. Dane wejściowe : d[] - zbiór elementów do posortowania. - każdy element posiada pole klucz, wg którego dokonuje się sortowania ( pole klucz jest liczbą całkowitą). N - liczba elementów w zbiorze d [ ], kmin - minimalna wartość klucza, kmin kmax - maksymalna wartość klucza, kmax Î C Dane wyjściowe : b[] - zbiór z posortowanymi elementami ze zbioru d[ ]. Zmienne pomocnicze : L[] - tablica liczników wartości kluczy (elementy są liczbami całkowitymi, a indeksy przyjmują kolejne wartości od kmin do kmax i - zmienna licznikowa pętli,

SORTOWANIE PRZEZ ZLICZANIE (Counting Sort) Lista kroków : Krok 1 : Dla i = kmin, kmin + 1, . . . , kmax: L[i] : = 0; Krok 2 : Dla i = 1, 2, . . . , n: L[d[i]. klucz] : = L[d[i]. klucz] + 1 Krok 3 : Dla i = kmin + 1, kmin + 2, . . . , kmax: L[i] : = L[i] + L[i - 1] Krok 4 : Dla i = n, n - 1, . . . , 1: wykonuj kroki 5 i 6 Krok 5 : b[L[d[i]. klucz]] : = d[i] Krok 6 : L[d[i]. klucz] : = L[d[i]. klucz] - 1 Krok 7 : Zakończ algorytm

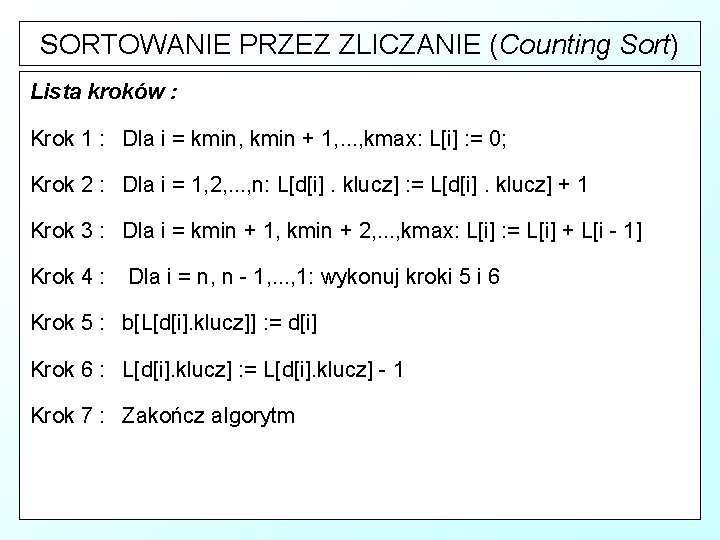
SORTOWANIE PRZEZ ZLICZANIE (Counting Sort) W pętli nr 1 przygotowujemy liczniki wystąpień poszczególnych kluczy ustawiamy je na 0. W pętli nr 2 przeglądamy kolejne elementy zbioru zwiększając o 1 licznik o numerze równym wartości klucza w sortowanym elemencie zbioru. W pętli numer 3 przekształcamy zliczone wartości wystąpień kluczy na ostatnie pozycje elementów z danym kluczem w zbiorze wyjściowym. W pętli nr 4 ponownie przeglądamy zbiór wejściowy i przesyłamy elementy ze zbioru wejściowego do zbioru wyjściowego na pozycję o numerze zawartym w liczniku skojarzonym z kluczem elementu.

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) & Mamymetod losowysortowania, zbiór liczb Algorytm ten jest jedną z ciekawszych gdyż jest on szybki oraz nie pochłania zbyt wiele zasobów z nich pamięci. Jego złożoność czasowa to. Tworzymy O(n log n), a kopiec pamięciowa O(1). Algorytm ten jest w praktyce z reguły nieco wolniejszy od sortowania szybkiego, ma lepszą Zamieniamylecz element znajdujący pesymistyczną złożoność czasową. się w korzeniu z ostatnim elementem w kopcu. Elementy przenoszone na Zrozumienie algorytmu wymaga zaznajomienia się z pojęciem koniec kopca tworzą część kopca/stogu. posortowaną (nie wchodzącą już w skład kopca) Kopiec jest to tablica danych, która da się przedstawić graficznie w postaci drzewa binarnego - każdy węzeł tego drzewa odpowiada jednemu elementowi tablicy. pozostały Naprawiamy kopiec (bez elementów Aby posortować elementy należy wykonać szereg operacji już posortowanych). w kolejności przedstawionej na schemacie.

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Drzewo binarne § § § Drzewo binarne jest hierarchiczną strukturą danych, którego elementy będziemy nazywali węzłami (ang. node) lub wierzchołkami. W hierarchii liniowej każdy element może posiadać co najwyżej jeden następnik. W drzewie binarnym każdy węzeł może posiadać dwa następniki, które nazywamy węzłami potomnymi danego węzła (ang. child node). Węzły są połączone krawędziami symbolizującymi następstwo kolejnych elementów w strukturze drzewa binarnego. Rodzicem lub węzłem nadrzędnym nazywamy węzeł leżący na wyższym poziomie hierarchii drzewa binarnego. Węzeł nie posiadający rodzica nazywamy korzeniem drzewa binarnego (ang. root node).

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Budowa drzewa binarnego Ø Ø Element d[1] będzie zawsze korzeniem drzewa. i-ty poziom drzewa binarnego zawiera do 2 i-1 elementów Ø węzły potomne mają indeksy równe: § 2 k - lewy potomek § 2 k+1 - prawy potomek Ø węzeł nadrzędny ma indeks równy [k div 2] A A B C D E F G C B D E F G

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Tworzenie kopca § Kopiec jest drzewem binarnym, w którym wszystkie węzły spełniają następujący warunek (zwany warunkiem kopca) : • § węzeł nadrzędny jest większy lub równy węzłom potomnym (w porządku malejącym relacja jest odwrotna - mniejszy lub równy). Konstrukcja kopca jest nieco bardziej skomplikowana od konstrukcji drzewa binarnego, ponieważ musimy dodatkowo troszczyć się o zachowanie warunku kopca. Zatem po każdym dołączeniu do kopca nowego węzła, sprawdzamy odpowiednie warunki i ewentualnie dokonujemy wymian węzłów na ścieżce wiodącej od dodanego węzła do korzenia.

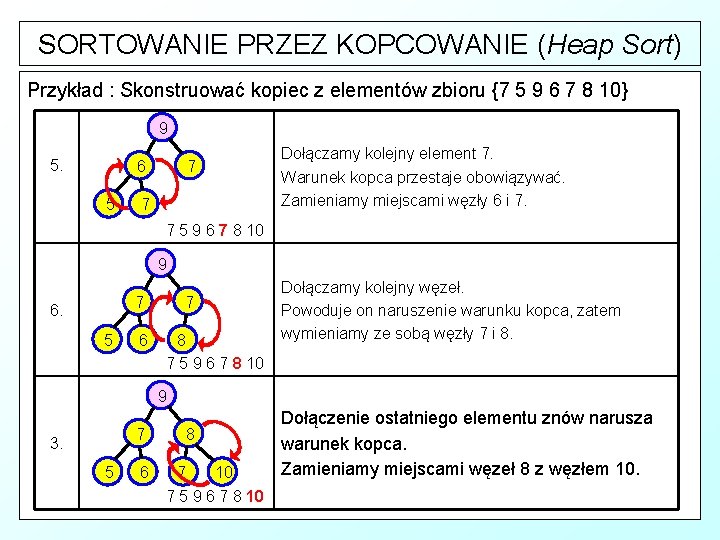
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Skonstruować kopiec z elementów zbioru {7 5 9 6 7 8 10} Lp. Operacja Opis 7 1. 7 5 9 6 7 8 10 7 2. Budowę kopca rozpoczynamy od pierwszego elementu zbioru, który staje się korzeniem. Do korzenia dołączamy następny element. Warunek kopca jest zachowany. 5 7 5 9 6 7 8 10 7 3. 9 5 7 5 9 6 7 8 10 9 5 4. 6 7 7 5 9 6 7 8 10 Dodajemy kolejny element ze zbioru. Po dodaniu elementu 9 warunek kopca przestaje być spełniony. Dołączamy kolejny element 6. Znów warunek kopca przestaje być spełniony - zamieniamy miejscami węzły 5 i 6.

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Skonstruować kopiec z elementów zbioru {7 5 9 6 7 8 10} 9 5. 7 6 5 7 Dołączamy kolejny element 7. Warunek kopca przestaje obowiązywać. Zamieniamy miejscami węzły 6 i 7. 7 5 9 6 7 8 10 9 7 7 6. 5 6 8 7 5 9 6 7 8 10 Dołączamy kolejny węzeł. Powoduje on naruszenie warunku kopca, zatem wymieniamy ze sobą węzły 7 i 8. 9 7 3. 5 6 8 7 10 7 5 9 6 7 8 10 Dołączenie ostatniego elementu znów narusza warunek kopca. Zamieniamy miejscami węzeł 8 z węzłem 10.

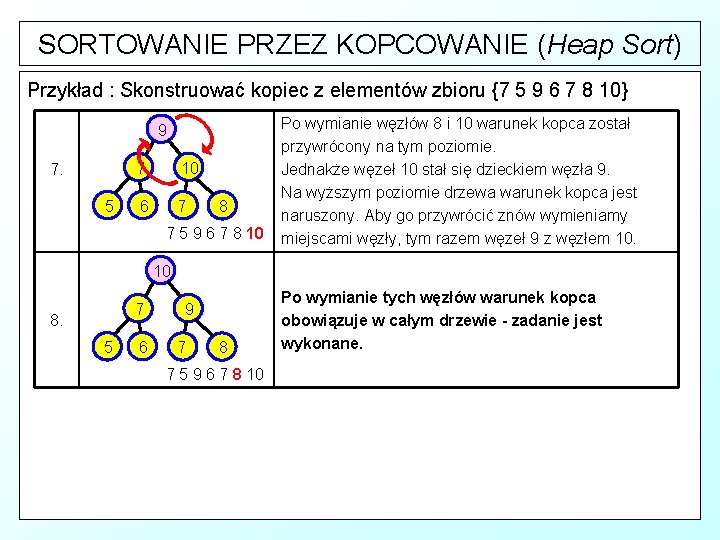
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Skonstruować kopiec z elementów zbioru {7 5 9 6 7 8 10} 9 7. 5 7 10 6 7 8 7 5 9 6 7 8 10 Po wymianie węzłów 8 i 10 warunek kopca został przywrócony na tym poziomie. Jednakże węzeł 10 stał się dzieckiem węzła 9. Na wyższym poziomie drzewa warunek kopca jest naruszony. Aby go przywrócić znów wymieniamy miejscami węzły, tym razem węzeł 9 z węzłem 10. 10 7 8. 5 6 9 7 8 7 5 9 6 7 8 10 Po wymianie tych węzłów warunek kopca obowiązuje w całym drzewie - zadanie jest wykonane.

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Specyfikacja algorytmu budowy kopca. Dane wejściowe : d[] - zbiór zawierający elementy do wstawienia do kopca. (numeracja elementów rozpoczyna się od 1), n - Ilość elementów w zbiorze, Dane wyjściowe : d[] - zbiór zawierający kopiec Zmienne pomocnicze : i - zmienna licznikowa pętli umieszczającej kolejne elementy zbioru w kopcu, i {2, 3, . . . , n} j, k - indeksy elementów leżących na ścieżce od wstawianego elementu do korzenia, x - zmienna pomocnicza przechowująca tymczasowo element wstawiany do kopca

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Lista kroków algorytmu budowy kopca. Krok 1 : Dla i = 2, . . . , n: wykonuj kroki 2. . . 5 Krok 2 : j : = i; k : = j div 2; Krok 3 : x : = d [ i ]; Krok 4 : Krok 5 : Krok 6 : Dopóki ( k > 0 ) and ( d [k] < x ) wykonuj : d [ j ] : = d [ k ]; j : = k; k : = j div 2; d [ j ] : = x; koniec

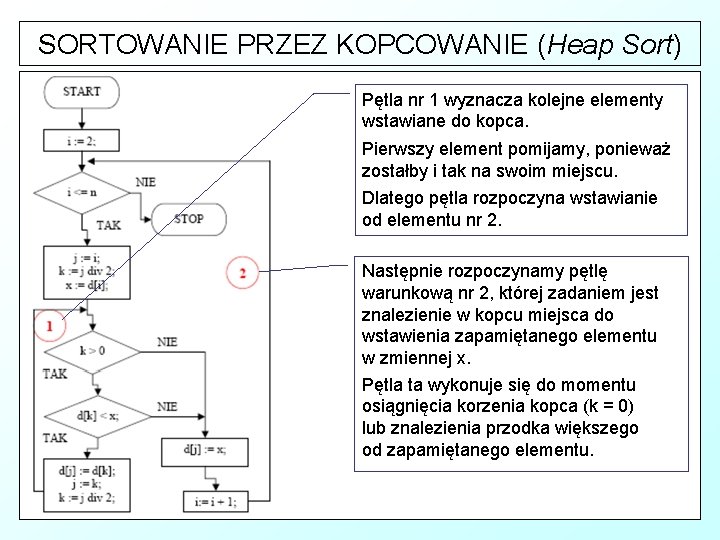
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Pętla nr 1 wyznacza kolejne elementy wstawiane do kopca. Pierwszy element pomijamy, ponieważ zostałby i tak na swoim miejscu. Dlatego pętla rozpoczyna wstawianie od elementu nr 2. Następnie rozpoczynamy pętlę warunkową nr 2, której zadaniem jest znalezienie w kopcu miejsca do wstawienia zapamiętanego elementu w zmiennej x. Pętla ta wykonuje się do momentu osiągnięcia korzenia kopca (k = 0) lub znalezienia przodka większego od zapamiętanego elementu.

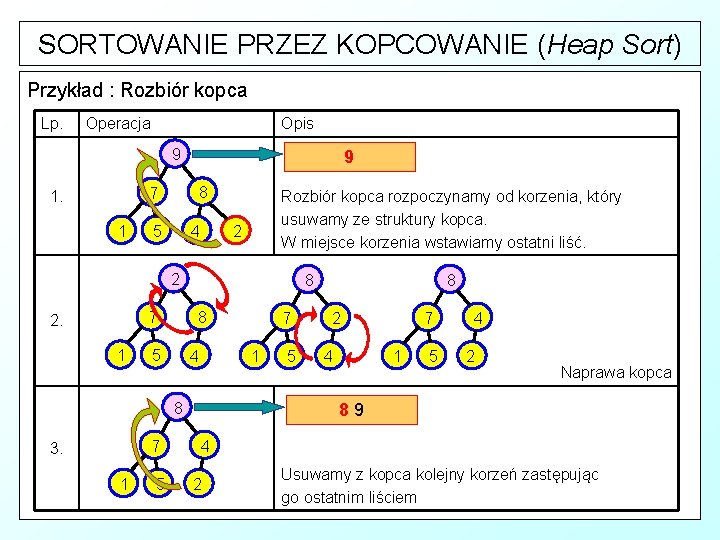
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Rozbiór kopca § Rozbiór kopca rozpoczynamy od korzenia, który usuwamy ze struktury kopca w miejsce korzenia wstawiamy ostatni liść. § Zasady rozbioru kopca : • • • Zamień miejscami korzeń z ostatnim liściem, który wyłącz ze struktury kopca – elementem pobieranym z kopca jest zawsze jego korzeń, czyli element największy. Jeśli jest to konieczne, przywróć warunek kopca idąc od korzenia w dół. Kontynuuj od kroku 1, aż kopiec będzie pusty.

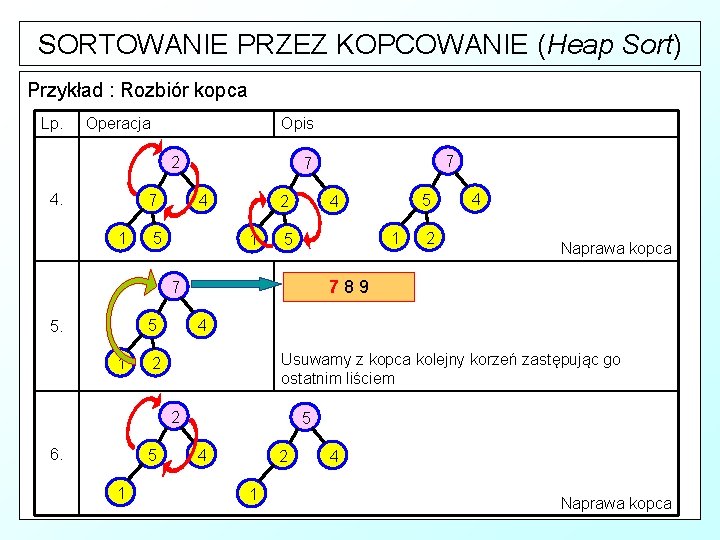
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Rozbiór kopca Lp. Operacja Opis 9 9 8 7 1. 1 5 4 Rozbiór kopca rozpoczynamy od korzenia, który usuwamy ze struktury kopca. W miejsce korzenia wstawiamy ostatni liść. 2 2 8 7 2. 1 5 4 7 1 5 7 1 8 3. 8 8 5 2 7 1 4 5 4 2 Naprawa kopca 89 4 2 Usuwamy z kopca kolejny korzeń zastępując go ostatnim liściem

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Rozbiór kopca Lp. Operacja Opis 2 4. 4 7 1 5 1 1 5 Usuwamy z kopca kolejny korzeń zastępując go ostatnim liściem 2 5 1 Naprawa kopca 789 2 6. 2 4 4 5 1 5 4 2 7 5. 7 7 5 4 2 1 4 Naprawa kopca

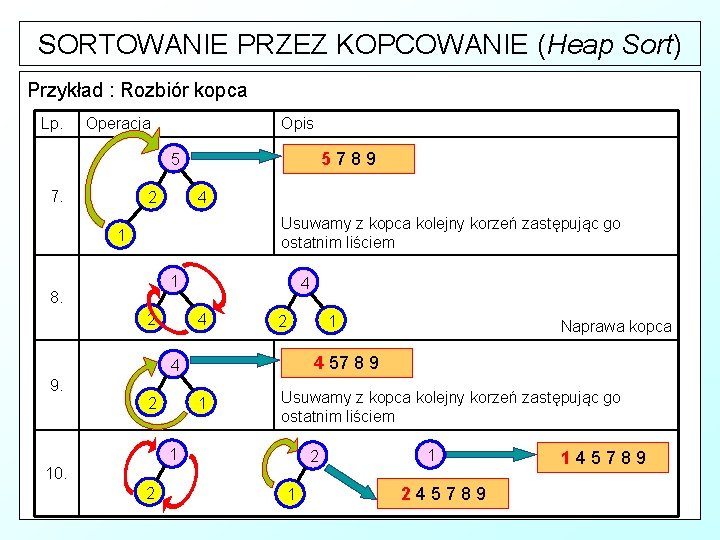
SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Przykład : Rozbiór kopca Lp. Operacja Opis 5789 5 7. 4 2 Usuwamy z kopca kolejny korzeń zastępując go ostatnim liściem 1 1 8. 4 4 2 1 2 4 57 8 9 4 9. 1 2 Usuwamy z kopca kolejny korzeń zastępując go ostatnim liściem 1 2 10. 2 Naprawa kopca 1 1 245789 145789

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Specyfikacja algorytmu rozbioru kopca. Dane wejściowe : d[] - zbiór zawierający elementy do wstawienia do kopca. (numeracja elementów rozpoczyna się od 1), n - Ilość elementów w zbiorze, Dane wyjściowe : d[] - zbiór zawierający elementy pobrane z kopca ułożone w porządku rosnącym, Zmienne pomocnicze : i - indeksy elementów leżących na ścieżce w dół od korzenia, i {n, n-1 , . . 2} j, k - indeksy elementów leżących na ścieżce w dół od korzenia, m - indeks większego z dwóch elementów potomnych.

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Lista kroków algorytmu rozbioru kopca. Krok 1 : Dla i = n, n-1 wykonuj kroki 2. . . 8 Krok 2 : d [1] d[ i ]; Krok 3 : j : = 1; k : = 2; Krok 4 : Krok 5 : Krok 6 : Krok 7 : Krok 8 : Krok 9 : Dopóki (k < i) wykonuj kroki 5. . . 8 Jeżeli (k + 1 < i) and (d[k + 1] > d[k]), to m : = k + 1. Inaczej m : = k Jeżeli d[m]<= d[j], to wyjdź z bieżącej pętli i kontynuuj następny obieg pętli z kroku 1 d[ j ] d[m] j : = m; k : = j + j i kontynuuj pętlę z kroku 4 Zakończ algorytm

SORTOWANIE PRZEZ KOPCOWANIE (Heap Sort) Pętla nr 1 zamienia miejscami kolejne liście ze spodu drzewa z korzeniem. Pętla przebiega wstecz indeksy elementów zbioru d[ ] poczynając od indeksu n a kończąc na indeksie 2. Element i-ty jest wymieniany z korzeniem kopca. Zadaniem pętli nr 2 jest przywrócenie w strukturze warunku kopca. Zmienna j przechowuje indeks przodka, zmienna k przechowuje indeks lewego potomka. Pętla kończy się, gdy węzeł j-ty nie posiada potomków.

SORTOWANIE DYSTRYBUCYJNE & Omawiane dotychczas algorytmy sortujące opierają się na sprawdzaniu uporządkowania zbioru, które polega na porównywaniu elementów. Udowodniono, iż barierą efektywności takich algorytmów w przypadku ogólnym (sortowanie zbioru o losowym rozkładzie elementów) jest klasa złożoności obliczeniowej Q(n log n). Zachodzi zatem naturalne pytanie: czy istnieją inne sposoby sortowania o niższej klasie złożoności obliczeniowej? Sortowanie pozycyjne Sortowanie kubełkowe

SORTOWANIE POZYCYJNE (Radix Sort) & Problem sortowania ciągów znaków lub liczb wielocyfrowych można rozwiązać wykorzystując sortowanie pozycyjne. Sortowanie to odbywa się w grupach od lewej do prawej lub odwrotnie. Jeśli chcemy posortować ciąg znaków (np. nazwiska) sortować będziemy od lewej do prawej, natomiast aby posortować liczby poruszmy się w odwrotnym kierunku § Wbrew pozorom sortowanie rozpoczynamy od pozycji najmniej znaczących (jedności) i poruszamy się w „lewo”. Złożoność takiego algorytmu wynosi kn, gdzie k to ilość cyfr w liczbie, co daje w notacji „wielkie Q” złożoność Q(n).

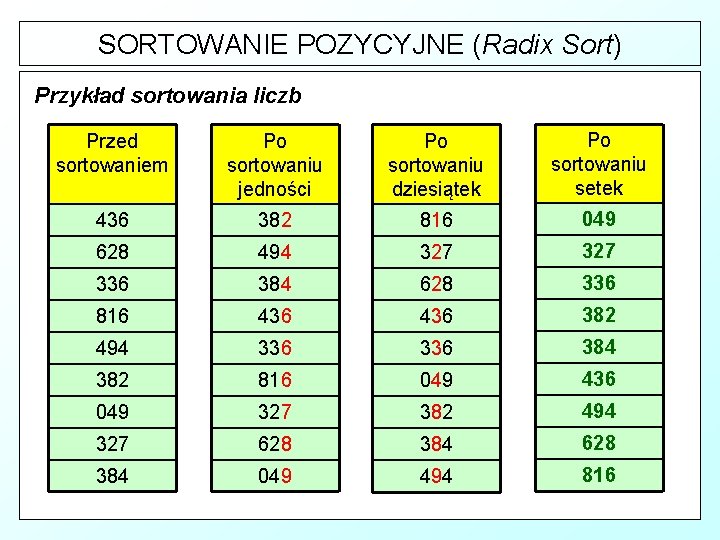
SORTOWANIE POZYCYJNE (Radix Sort) Przykład sortowania liczb Przed sortowaniem Po sortowaniu jedności Po sortowaniu dziesiątek Po sortowaniu setek 436 382 816 049 628 494 327 336 384 628 336 816 436 382 494 336 384 382 816 049 436 049 327 382 494 327 628 384 049 494 816

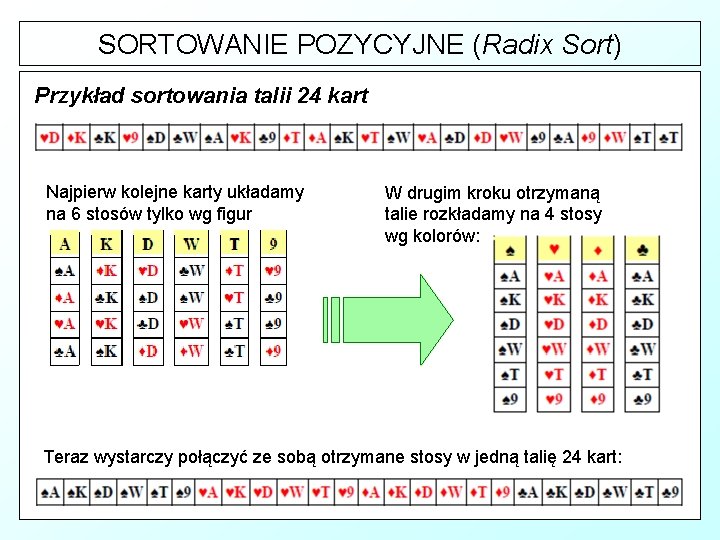
SORTOWANIE POZYCYJNE (Radix Sort) Przykład sortowania talii 24 kart Najpierw kolejne karty układamy na 6 stosów tylko wg figur W drugim kroku otrzymaną talie rozkładamy na 4 stosy wg kolorów: Teraz wystarczy połączyć ze sobą otrzymane stosy w jedną talię 24 kart:

SORTOWANIE KUBEŁKOWE (Bucket Sort) & Algorytm sortowania kubełkowego pozwala sortować zbiory liczb całkowitych - najlepiej o dużej ilości elementów, lecz o małym zakresie. v Zasada działania jest następująca: Określamy zakres wartości, jakie mogą przyjmować elementy sortowanego zbioru (wmin ÷ wmax). Dla każdej możliwej wartości przygotowujemy kubełek-licznik, który będzie zliczał ilość wystąpień tej wartości w sortowanym zbiorze. Liczba liczników jest równa (wmax - wmin + 1) i każdy z nich jest początkowo ustawiony na wartość zero. Przeglądamy kolejno elementy zbioru od pierwszego do ostatniego i dla każdego elementu zbioru zwiększamy o jeden zawartość licznika o numerze równym wartości elementu. Przeglądamy kolejne liczniki zapisując do zbioru wynikowego ich numery tyle razy, ile wynosi ich zawartość.

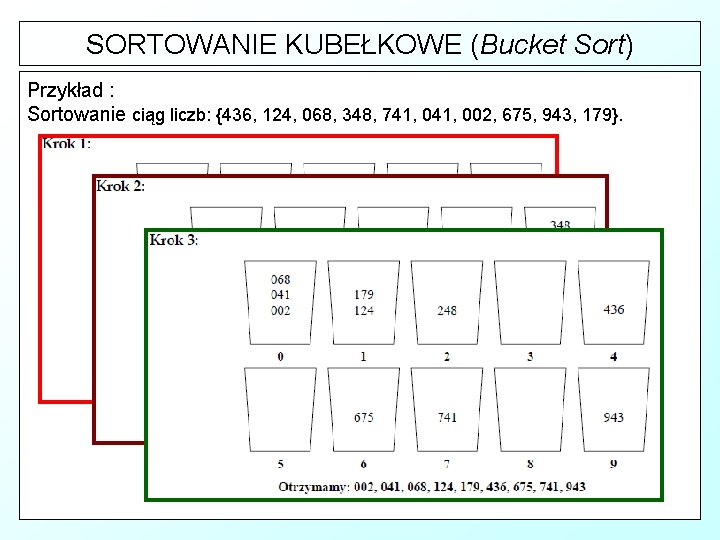
SORTOWANIE KUBEŁKOWE (Bucket Sort) Przykład : Sortowanie ciąg liczb: {436, 124, 068, 348, 741, 002, 675, 943, 179}.

SORTOWANIE KUBEŁKOWE (Bucket Sort) Specyfikacja algorytmu sortowania kubełkowego. Dane wejściowe : d[] - sortowany zbiór liczb całkowitych (indeksy elementów rozpoczynają się od 1), n - liczba elementów w zbiorze, wmin - minimalna wartość elementu zbioru, wmax - maksymalna wartość elementu zbioru, Dane wyjściowe : d [ ] - Zbiór zawierający elementy posortowane, Zmienne pomocnicze : Lw [ ] - tablica liczników wartości o indeksach od wmin do wmax. Każdy licznik przechowuje liczbę całkowitą i, j - zmienne licznikowe pętli, i, j.

SORTOWANIE KUBEŁKOWE (Bucket Sort) Lista kroków algorytmu sortowania kubełkowego. Krok 1 : Dla i = wmin , wmin + 1, . . . , wmax: wykonuj w[i] : = 0 Krok 2 : Dla i = 1, 2, . . . , n: wykonuj d[i] ] : = Lw [d[i] ] + 1 Krok 3 : j : = 1; Krok 4 : Dla i = wmin , wmin + 1, . . . , wmax: wykonuj kroki 5. . . 8 Krok 5 : Dopóki Lw[i] > 0 wykonuj kroki 6. . . 8 Krok 6 : d[j] : = i Krok 7 : Lw[i] : = Lw[i] – 1 Krok 8 : j : = j + 1 Krok 9 : zakończ algorytm

SORTOWANIE KUBEŁKOWE (Bucket Sort) Pętla nr 1 zeruje kolejne liczniki L_w[ ]. W pętli nr 2 przeglądamy kolejne elementy zbioru od pierwszego do ostatniego. Dla każdego elementu zwiększamy licznik o numerze równym wartości elementu. Po zakończeniu tej pętli liczniki zawierają liczbę wystąpień poszczególnych wartości elementów w sortowanym zbiorze. Pętla nr 3 przegląda kolejne liczniki. Jeśli zawartość danego licznika jest większa od zera, to pętla nr 4 umieści w zbiorze wyjściowym odpowiednią ilość numerów licznika, które odpowiadają zliczonym wartościom elementów ze zbioru wejściowego.