WYKAD 2 Algorytmy rekurencyjne Ryszard Myhan ALGORYTMY REKURENCJNE

WYKŁAD 2 Algorytmy rekurencyjne Ryszard Myhan

ALGORYTMY REKURENCJNE v Rekurencja zwana także rekursją jest jedną z najważniejszych metod konstruowania rozwiązań i algorytmów. v Zgodnie ze znaczeniem informatycznym: § § algorytm rekurencyjny to taki który korzysta z samego siebie, program rekurencyjny to taki który wywołuje sam siebie. v Cechy algorytmów rekurencyjnych: Przykładem rekurencji jest prosty algorytm „jedz § zakończenie algorytmu jest jasno określonekaszkę”: § 1. złożony problem zostaje rozłożony na: Jedz kaszkę (weź łyżkę kaszki i połknij) o problemy elementarne, które umiemy rozwiązać, 2. Jedz kaszkę dalej, aż talerz będzie pusty o na problemy o mniejszym stopniu komplikacji, niż ten z którym mieliśmy do czynienia na początku.

TECHNIKA REKURENCJI v W informatyce można realizować szczególny rodzaj powtórzeń bez wymogu stosowania pętli – technikę rekurencji. Ä Z techniką tą spotykamy się w życiu codziennym, jej przykładem jest odbicie w lustrze: jeśli popatrzymy w lustro, a za sobą odpowiednio ustawimy drugie, to zauważymy, że odbija się w nim obraz z lustra, które mamy przed sobą. Ä Kolejnym przykładem może być obraz, w którym wkomponowany jest ten sam obraz. W każdym z tych przykładów dany obraz jest częścią samego siebie. Ä Przykładem rekurencji może być: Wieża Hanoi, algorytm Euklidesa lub rekurencyjny ciąg Fibonacciego.

DEFINICJA REKURENCJI v Definicja rekurencyjna składa się z dwóch części. W pierwszej, zwanej podstawową lub warunkiem początkowym są wyliczone elementy podstawowe, stanowiące części składowe wszystkich pozostałych elementów zbioru. W drugiej części, zwanej krokiem indukcyjnym, są podane reguły umożliwiające konstruowanie nowych obiektów z elementów podstawowych lub obiektów zbudowanych wcześniej. Ä Reguły te można stosować wielokrotnie, tworząc kolejne nowe obiekty.

WYWOŁANIE FUNKCJI REKURENCJNEJ v Kolejne wywołania funkcji rekurencyjnej są związane z odkładaniem na stosie programu kolejnych rekordów aktywacji funkcji. v W wyniku kończenia działania poszczególnych funkcji na kolejnych poziomach rekurencji kolejne rekordy aktywacji są zdejmowane ze stosu

PROGRAMY REKURENCJNE v Programy rekurencyjne są najczęściej krótkie i zwięzłe, ponieważ w pewnym sensie odzwierciedlają naturalny sposób ludzkiego myślenia. v Jednak mają też poważne wady: § są wolne; § wykorzystują dużo pamięci operacyjnej. Ä Przy każdym wywołaniu jakiejś procedury na stos trafia adres spod którego nastąpiło jej wywołanie, oraz wszystki parametry i zmienne lokalne. § Zawsze można zmienić procedurę rekurencyjną na wersję iteracyjną, a czasami nawet na wzór ogólny § W niektórych przypadkach jest to bardzo opłacalne, w innych tylko komplikuje program.

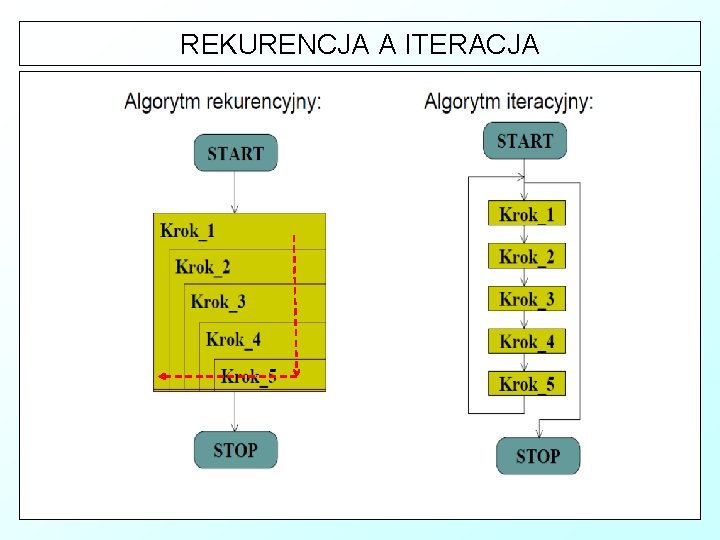
REKURENCJA A ITERACJA

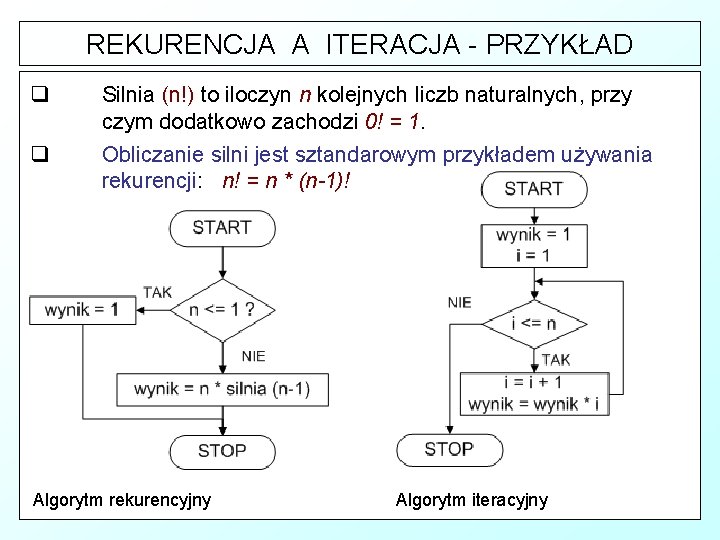
REKURENCJA A ITERACJA - PRZYKŁAD q q Silnia (n!) to iloczyn n kolejnych liczb naturalnych, przy czym dodatkowo zachodzi 0! = 1. Obliczanie silni jest sztandarowym przykładem używania rekurencji: n! = n * (n-1)! Algorytm rekurencyjny Algorytm iteracyjny

REKURENCJA A ITERACJA - PRZYKŁAD Algorytm rekurencyjny function Silnia. R(Liczba : Longint) : Longint ; begin if Liczba < 0 then begin Result : = 0 ; Exit ; end ; Result : = 1 ; if Liczba < 2 then Exit ; Result : = Result * Liczba ; if Liczba > 1 then Result : = Result * Silnia. R(Liczba - 1) end ; Algorytm iteracyjny function Silnia. I(Liczba : Longint) : Longint ; var i : Integer ; begin if Liczba < 0 then begin Result : = 0 ; Exit ; end ; Result : = 1 ; if Liczba < 2 then Exit ; for i : = 1 to Liczba do Result : = Result * i ; end ;

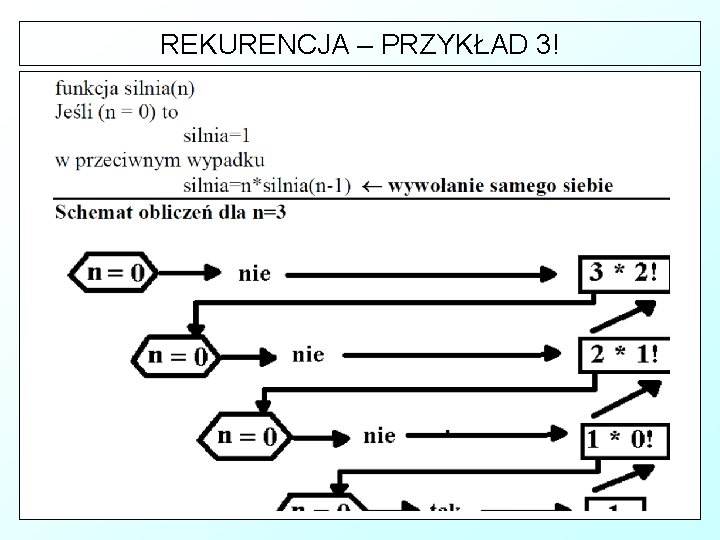
REKURENCJA – PRZYKŁAD 3!

REKURENCJA – SCHEMAT HORNERA q Schemat Hornera to bardzo powszechna metoda stosowana do rozwiązywania wielu zadań min. do znajdowania reprezentacji liczby w innych systemach liczenia. Ä Rozważmy zadanie policzenia wartości wielomianu stopnia n: y = Wn(x) = a 0*xn + a 1*xn-1+ a 2*xn-2 +. . . + an-1*x + an Ä Zgodnie ze schematem Hornera można zapisać w postaci: Y = Wn(x) = = (a 0*xn-1 + a 1*xn-2+ a 2*xn-3 +. . . + an-1)*x +an = = Wn-1(x)*x + an = = ((a 0*xn-2 + a 1*xn-3+ a 2*xn-4 +. . . + an-2)*x+ an-1)*x +an = = (Wn-2(x)*x + an-1)*x + an = = (. . . (( a 0*x+ a 1)*x + a 2)*x +. . . + an-1)*x +an = = (. . . (( W 1(x)*x + a 2)*x +. . . + an-1)*x +an

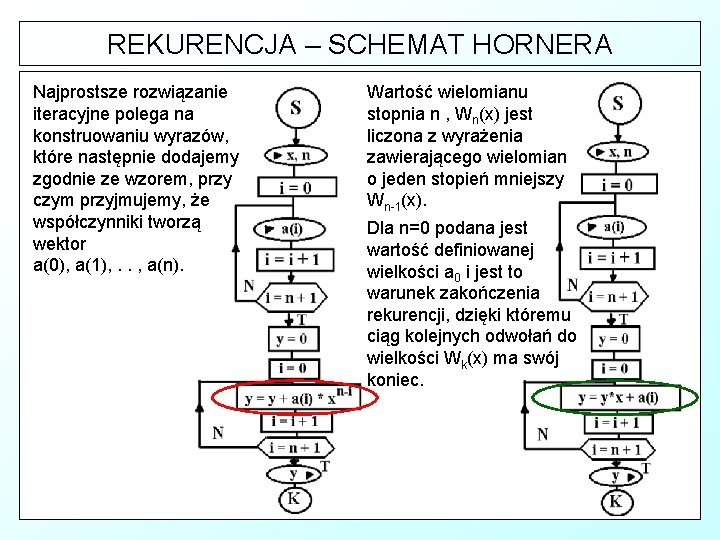
REKURENCJA – SCHEMAT HORNERA

REKURENCJA – SCHEMAT HORNERA Najprostsze rozwiązanie iteracyjne polega na konstruowaniu wyrazów, które następnie dodajemy zgodnie ze wzorem, przy czym przyjmujemy, że współczynniki tworzą wektor a(0), a(1), . . , a(n). Wartość wielomianu stopnia n , Wn(x) jest liczona z wyrażenia zawierającego wielomian o jeden stopień mniejszy Wn-1(x). Dla n=0 podana jest wartość definiowanej wielkości a 0 i jest to warunek zakończenia rekurencji, dzięki któremu ciąg kolejnych odwołań do wielkości Wk(x) ma swój koniec.

ALGORYTM EUKLIDESA v Algorytm Euklidesa jest jednym z najstarszych przepisów – schematów obliczeń. v Jego zadaniem jest znalezienie największego wspólnego dzielnika dwóch liczb całkowitych (NWD) - jest to potrzebne na przykład przy skracaniu ułamków. Ä Opiera się on na fakcie, że jeśli od większej liczby odejmie się mniejszą, to ta mniejsza liczba i otrzymana różnica będą miały taki sam największy wspólny dzielnik jak pierwotne liczby. Ä Gdy przy kolejnym odejmowaniu otrzyma się parę takich samych liczb, to oznacza że znaleziono NWD.

ALGORYTM EUKLIDESA W algorytmie wykorzystywana jest zależność: Dane wejściowe: a, b – dwie liczby naturalne Dane wyjściowe: liczba naturalna będąca największym wspólnym dzielnikiem liczb a i b. Metoda: • W pierwszej sekcji algorytmu sprawdzamy czy a>b i jeżeli tak jest to zamieniamy miejscami wartości zmiennych a i b, aby był spełniony wymagany warunek a<=b, • Sprawdzamy, czy b≠ 0, jeśli tak, to następne czynności wykonujemy aż do momentu gdy b=0 c = (b, a mod b); a = b; b = c • Wynik jest w zmiennej a

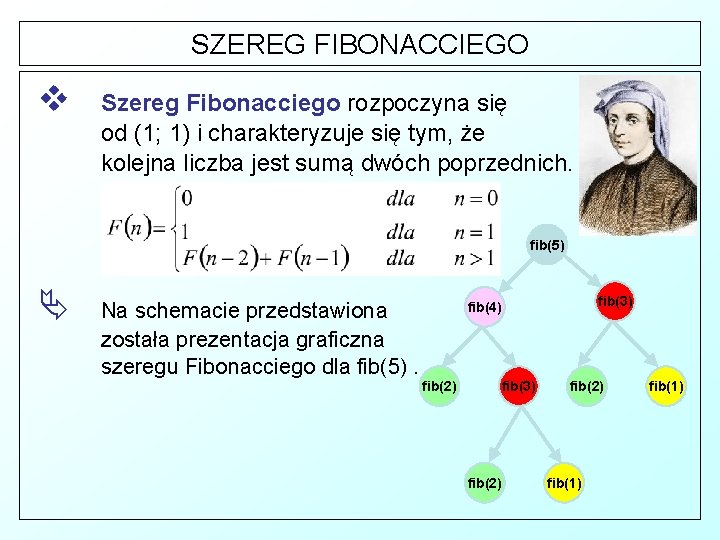
SZEREG FIBONACCIEGO v Szereg Fibonacciego rozpoczyna się od (1; 1) i charakteryzuje się tym, że kolejna liczba jest sumą dwóch poprzednich. fib(5) Ä Na schemacie przedstawiona została prezentacja graficzna szeregu Fibonacciego dla fib(5). fib(3) fib(4) fib(2) fib(3) fib(2) fib(1)

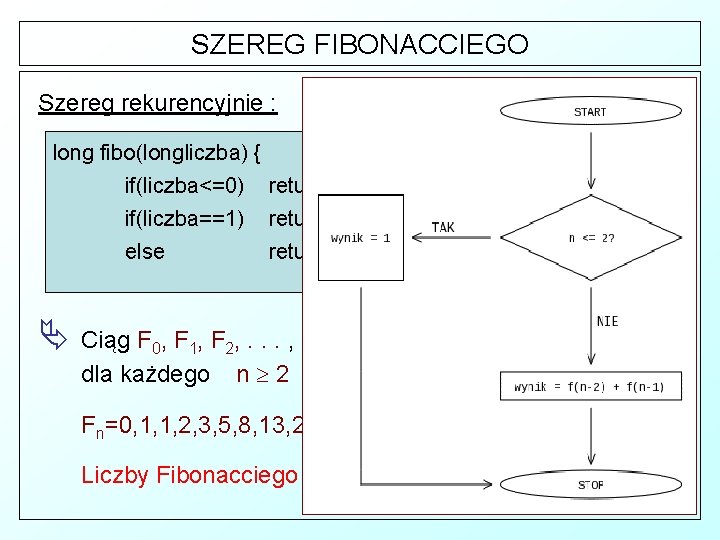
SZEREG FIBONACCIEGO Szereg rekurencyjnie : long fibo(longliczba) { if(liczba<=0) return 0; if(liczba==1) return 1 else return fibo(liczba-1)+fibo(liczba-2); } Ä Ciąg F 0, F 1, F 2, . . . , gdzie F 0 =0, F 1 = 1, F 2 = 1, F 3 = 2; dla każdego n 2 Fn = Fn− 1 + Fn− 2 , Fn=0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . . Liczby Fibonacciego rosną wykładniczo!

SZEREG FIBONACCIEGO v Rekurencyjna implementacja ciągu Fibonacciego jest niezwykle nieefektywna. v Stos programu nie jest praktycznie w stanie zrealizować tego algorytmu już dla liczb większych od 9 - oznacza to, że program ma zbyt dużą „złożoność pamięciową”. Ä Można wykazać że liczba wywołań funkcji Fib() w celu obliczenia wartości Fib(n) wynosi 2*Fib(n+1)-1 § Przykładowo obliczenie dwudziestej liczby Fibonacciego wymaga 220 (miliony) wywołań.

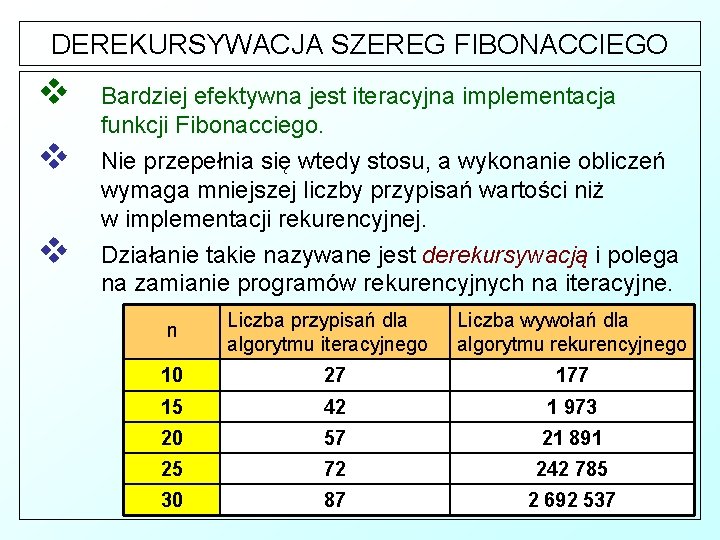
DEREKURSYWACJA SZEREG FIBONACCIEGO v Bardziej efektywna jest iteracyjna implementacja funkcji Fibonacciego. v Nie przepełnia się wtedy stosu, a wykonanie obliczeń wymaga mniejszej liczby przypisań wartości niż w implementacji rekurencyjnej. v Działanie takie nazywane jest derekursywacją i polega na zamianie programów rekurencyjnych na iteracyjne. n Liczba przypisań dla algorytmu iteracyjnego Liczba wywołań dla algorytmu rekurencyjnego 10 27 177 15 42 1 973 20 57 21 891 25 72 242 785 30 87 2 692 537

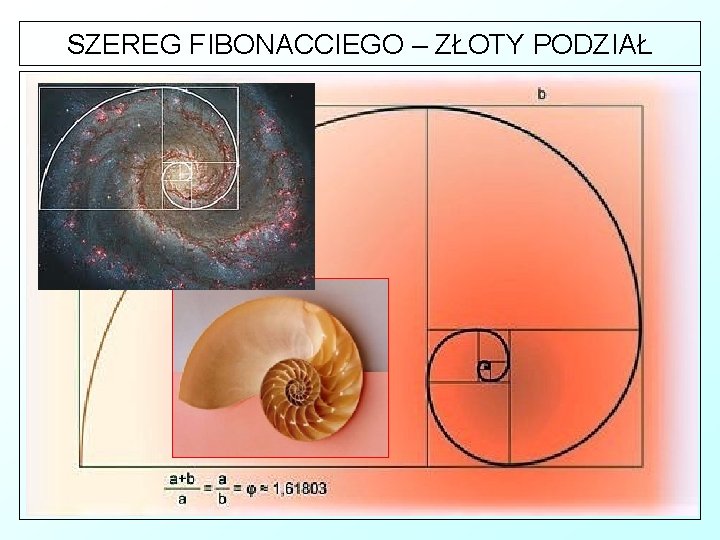
SZEREG FIBONACCIEGO v Fibonacci nawet nie zdawał sobie sprawy, że wzmianka o ciągu który umieścił na marginesie księgi Liber Abaci opisuje tak wiele zjawisk w przyrodzie. Ø Szereg Fibonacciego ściśle wiąże się z geometrią i sztuką – zjawiska oparte na nim sprawiają, że są atrakcyjne dla ludzkich zmysłów.

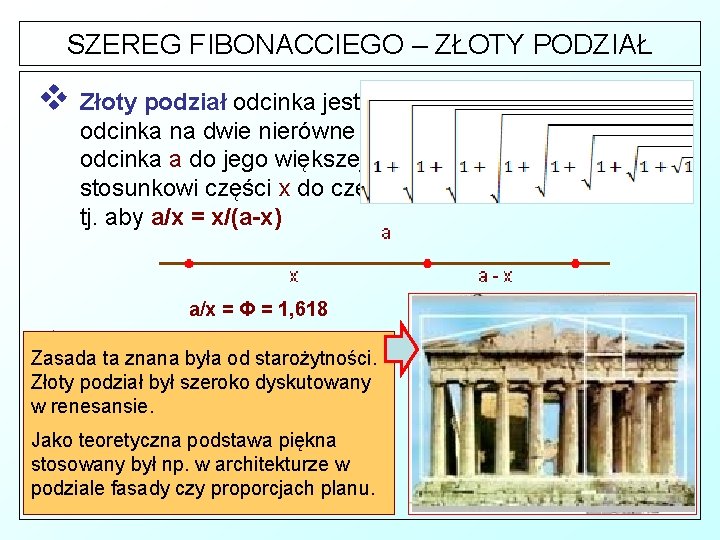
SZEREG FIBONACCIEGO – ZŁOTY PODZIAŁ v Złoty podział odcinka jest to wewnętrzny podział tego odcinka na dwie nierówne części tak, aby stosunek odcinka a do jego większej części x był równy stosunkowi części x do części mniejszej (a-x), tj. aby a/x = x/(a-x) a/x = Φ = 1, 618 v x/(a-x) = Φ = 1, 618 Własności takie wykazują elementy ciągu Fibonacciego Zasada ta znana była od starożytności. Złoty podział był szeroko dyskutowany w renesansie. Jako teoretyczna podstawa piękna stosowany był np. w architekturze w podziale fasady czy proporcjach planu.

SZEREG FIBONACCIEGO – ZŁOTY PODZIAŁ

WIEŻE HANOI J Rozwiązanie jest często spotykanym modelem myślenia rekurencyjnego. § Mamy n krążków o malejących średnicach. § Każdy z nich posiada wydrążony otwór i jest "nadziany" na pierwszy z trzech drążków. § Pozostałe drążki są puste. K Zadanie polega na przeniesieniu wszystkich krążków z pierwszego drążka na drugi przy użyciu trzeciego. L Trzeba to jednak zrobić przy dwóch założeniach: 1. wolno przenosić krążki tylko pojedynczo 2. ani przez moment krążek większy nie może leżeć na krążku mniejszym

WIEŻE HANOI & Zagadka stała się znana w XIX wieku dzięki matematykowi Édouardowi Lucasowi, który proponował zagadkę dla 8 krążków. o Do sprzedawanego zestawu była dołączona (prawdopodobnie wymyślona przez Lucasa) tybetańska legenda, według której mnisi w świątyni Brahmy rozwiązują tę łamigłówkę dla 64 złotych krążków. o Legenda mówi, że gdy mnisi zakończą zadanie, nastąpi koniec świata. : Zakładając, że wykonują 1 ruch na sekundę, ułożenie wieży zajmie 264− 1 = 18 446 744 073 709 551 615 (blisko 18 i pół tryliona) sekund, czyli około 584 542 miliardów lat. Ä Dla porównania: Wszechświat ma około 13, 7 mld lat.

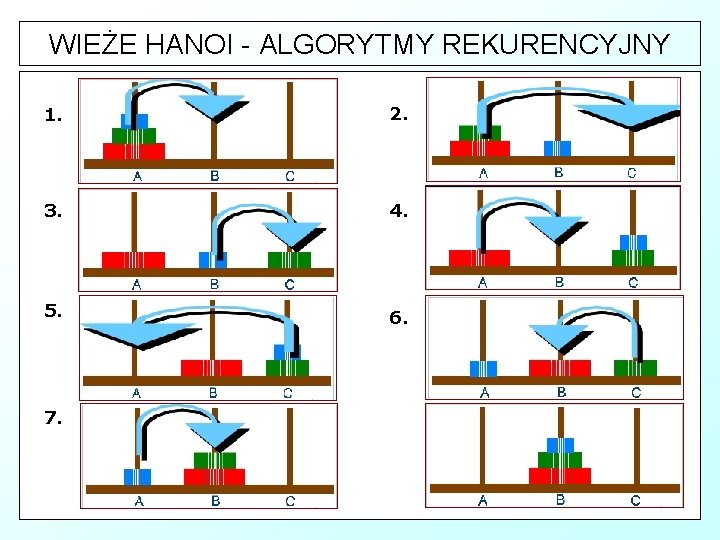
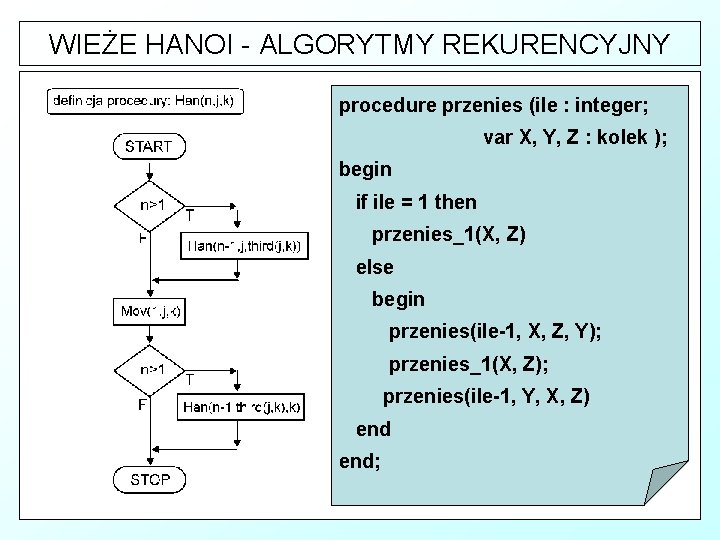
WIEŻE HANOI - ALGORYTMY REKURENCYJNY Ä Ä ] oznaczmy podstawki przez A, B, C numerujmy krążki od najmniejszego u góry do największego u dołu (gdzie n oznacza liczbę krążków) W celu przeniesienia n krążków z A do B należy: § przenieść n-1 krążków z A do C § § przenieść n-ty (największy) krążek z A do B przenieść n-1 krążków z C do B

WIEŻE HANOI - ALGORYTMY REKURENCYJNY 1. 2. 3. 4. 5. 6. 7.

WIEŻE HANOI - ALGORYTMY REKURENCYJNY procedure przenies (ile : integer; var X, Y, Z : kolek ); begin if ile = 1 then przenies_1(X, Z) else begin przenies(ile-1, X, Z, Y); przenies_1(X, Z); przenies(ile-1, Y, X, Z) end;

REKURENCJA BEZ KOŃCA Stad. Do. Wiecznosci(n) begin if (n=1) return 1; else begin if ((n%2)=0) // czy n jest parzyste? return Stad. Do. Wiecznosci(n-2)*n; else return Stad. Do. Wiecznosci(n-1)*n; end

FRAKTALE A REKURENCJA v Główną cechą fraktali jest samopodobieństwo. Ä Część fraktala jest podobna do całości tak, że w wielu przypadkach nie potrafilibyśmy odróżnić obrazu całej figury od jej wycinka wielokrotnie powiększonego. Ä Każdy fraktal składa się z nieskończonej liczby małych kopii siebie lub swoich fragmentów. v Fraktale określa się za pomocą zależności rekurencyjnych. Ä Oznacza to, że aby uzyskać fraktal, trzeba posłużyć się rekurencją, czyli wynik pewnych transformacji należy ponownie przekształcić przez te transformacje, i tak w nieskończoność.

FRAKTALE – KRZYWA KOCHA @ Konstrukcję krzywej Kocha najlepiej podać za pomocą algorytmu rekurencyjnego narysuj odcinek, podziel odcinek na trzy równe części, zamiast środkowej wstaw trójkąt równoboczny i usuń jego podstawę, dla każdego odcinka w otrzymanej w ten sposób figurze zrób to, co jest opisane w punkcie 2, wróć do punktu 3. Krok 1 Krok 3 Krok 2 Krok 4

FRAKTALE – ŚNIEŻYNA KOCHA @ Konstrukcja geometryczna za pomocą algorytmu rekurencyjnego narysuj trójkąt równoboczny, podziel każdy z boków na trzy równe części, zamiast środkowej wstaw trójkąt równoboczny i usuń jego podstawę, dla każdego odcinka w otrzymanej w ten sposób figurze zrób to, co jest opisane w punkcie 2, wróć do punktu 3. Krok 1 Krok 2 Krok 3 Krok 4

FRAKTALE – DYWAN SIERPIŃSKIEGO @ Od znakomitego polskiego matematyka, profesora Wacława Sierpińskiego pochodzi przepis na trójkątny dywan Sierpińskiego. weź trójkąt równoboczny, podziel go na 4 trójkąty podobne do niego w skali 1/2 i usuń część środkową, te same czynności powtórz z pozostałymi z podziału trzema trójkątami (podziel je i wyrzuć środek) i tak dalej, aż skończy się rozdzielczość ekranu. Krok 1 Krok 2 Krok 3

FRAKTALE – DYWAN SIERPIŃSKIEGO {Delphi} {$R *. DFM} procedure KONTUR(x, y, a: Integer); {narysuj trójkąt równoboczny o boku a i środku (x, y)} var p, hp: Integer; begin p: =a div 2; {połowa długości boku} hp: =Round(0. 433*a); {połowa wysokości} with Form 1. canvas do begin Pen. Color: =cl. White; Move. To(x, y-hp); {brzeg dużego trójkąta} Line. To(x+p, y+hp); Line. To(x-p, y+hp); Line. To(x, y-hp); Brush. Color: =cl. Red; Flood. Fill(x, y, cl. White, fs. Border); {wypełnienie} end; procedure WYTNIJ(n, x, y, a: Integer); {n-stopień rekurencji} {x, y-środek wycinanego trójkąta} {a - bok wycinanego trójkąta} var p, hp, q, r: Integer; begin p: =a div 2; q: =a div 4; if q<1 then Exit; hp: =Round(0. 433*a); {narysuj wycinany trójkąt} with Form 1. Canvas do begin Move. To(x, y+hp); {i wypełnij go kolorem tła formularza} Line. To(x-q, y); Line. To(x+q, y); Line. To(x, y+hp); Flood. Fill(x, y+1, cl. White, fs. Border); if n>1 then begin r: =Round(0. 2165*a); WYTNIJ(n-1, x, y-r, p); WYTNIJ(n-1, x+q, y+r, p); WYTNIJ(n-1, x-q, y+r, p); end; procedure TForm 1. Spin. Edit 1 Change(Sender: TObject); var x 0, y 0, bok, i: Integer; begin bok: =480; {bok całego dywanu} x 0: =Client. Width div 2; {środek formularza} y 0: =Client. Height div 2; refresh; KONTUR(x 0, y 0, bok); canvas. Brush. Color: =Form 1. Color; i: =Spin. Edit 1. Value; if i>0 then WYTNIJ(i, x 0, y 0, bok); end; end.

FRAKTALE - GĄBKA MENGERA v Trójwymiarowe uogólnienie dywanu Sierpińskiego.

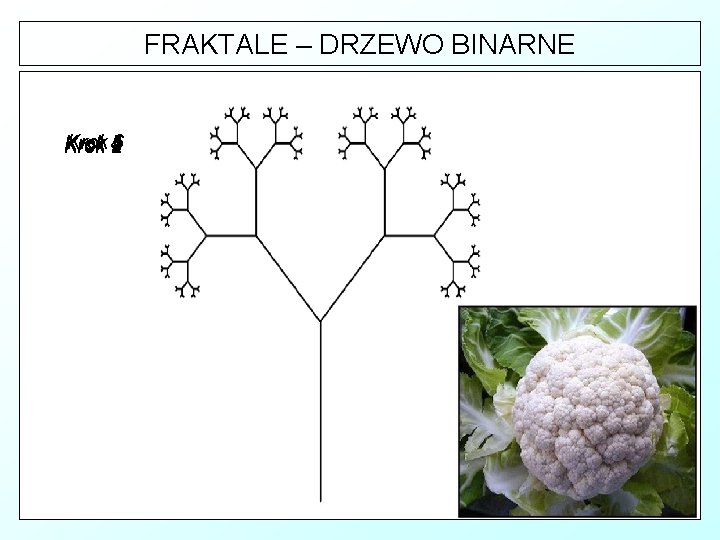
FRAKTALE – DRZEWO BINARNE Krok 6 Krok 5 Krok 4 Krok 3 Krok 1 Krok 2

FRAKTALE – PRZYKŁAD