W przestrzeni Zofia Miechowicz Otwock 27 01 2012

W przestrzeni Zofia Miechowicz Otwock 27. 01. 2012

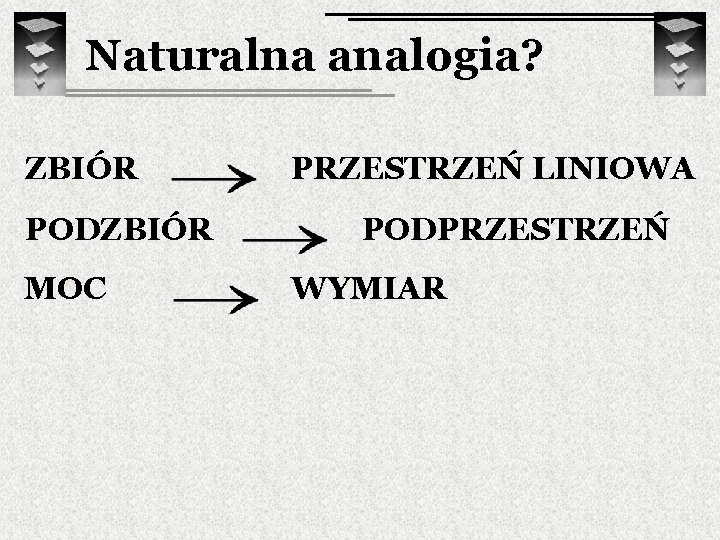
Naturalna analogia? ZBIÓR PODZBIÓR MOC PRZESTRZEŃ LINIOWA PODPRZESTRZEŃ WYMIAR

Ile tego jest? Podzbiorów k-elementowych zbioru n-elementowego Podprzestrzeni k-wymiarowych przestrzeni n-wymiarowej F – skończone ciało rzędu q

Ile tego jest? Podprzestrzeni k-wymiarowych przestrzeni n-wymiarowej F – skończone ciało rzędu q - niezależne Na ile sposobów? . . .

Ile tego jest? F – skończone ciało rzędu q - niezależne Na ile sposobów? Ile mają baz?

Ile tego jest? Podzbiorów k-elementowych zbioru n-elementowego Podprzestrzeni k-wymiarowych przestrzeni n-wymiarowej F – skończone ciało q elementowe

Ile tego jest? - Współczynnik dwumianowy Newtona Isaac Newton 1643 -1727 - Współczynnik dwumianowy Gaussa Do znalezienia formuły na sumy Gaussa Carl Friedrich Gauss 1777 -1855

Ile tego jest? Jako funkcja zmiennej q

Ile tego jest? - niezależne Donald Knuth 1938 ZREDUKOWANA POSTAĆ SCHODKOWA elementarne operacje na wierszach • pierwszy niezerowy element od lewej w każdym wierszu to 1 • wszystkie pozostałe elementy w kolumnie, w której jest jedynka wiodąca to zera • w każdym wierszu jedynka wiodąca pojawia się na prawo od jedynki wiodącej w poprzednim wierszu JEŻELI DWIE MACIERZE W TEJ POSTACI GENERUJĄ WIERSZOWO TĘ SAMĄ PRZESTRZEŃ, TO SĄ RÓWNE

Ile tego jest? Donald Knuth 1938

Ile tego jest? Donald Knuth 1938 • w każdym wierszu usuń wszystkie elementy na lewo od jedynki wiodącej

Ile tego jest? Donald Knuth 1938 • w każdym wierszu usuń wszystkie elementy na lewo od jedynki wiodącej

Ile tego jest? Donald Knuth 1938 • w każdym wierszu usuń wszystkie elementy na lewo od jedynki wiodącej • usuń kolumny, zawierające pierwsze jedynki

Ile tego jest? Donald Knuth 1938 • w każdym wierszu usuń wszystkie elementy na lewo od jedynki wiodącej • usuń kolumny, zawierające pierwsze jedynki

Ile tego jest? k Donald Knuth 1938 n-k Podprzestrzeni k-wymiarowych przestrzeni n-wymiarowej jest tyle samo, co takich obrazków • w każdym wierszu usuń wszystkie elementy na lewo od jedynki wiodącej • usuń kolumny, zawierające pierwsze jedynki • zamień wszystkie pozostałe elementy na *

Ile tego jest? WRACAMY! Donald Knuth 1938 100 010 0 , 1

Ile tego jest? WRACAMY! Donald Knuth 1938 1 0 0 0 * * 1 0 * * 0 1 * *

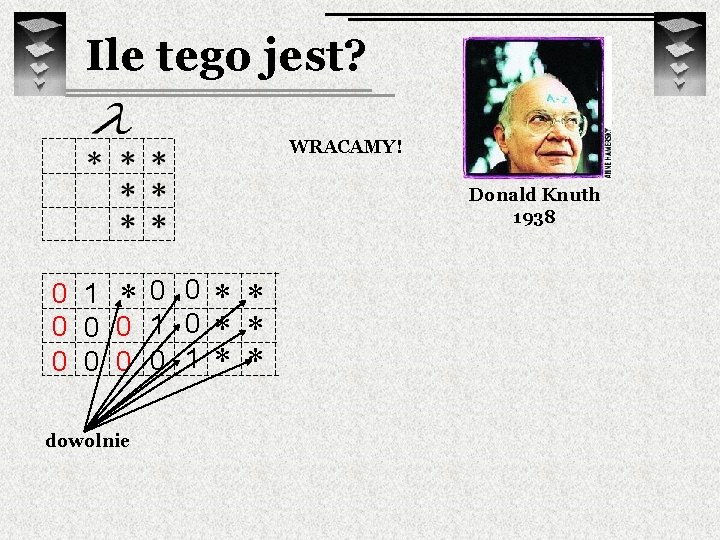
Ile tego jest? WRACAMY! Donald Knuth 1938 0 1 * 0 0 0 0 0 1 dowolnie * * *

Ile tego jest? WRACAMY! Donald Knuth 1938 0 1 2 0 0 1 0 3 1 0 0 1 0 1 dowolnie na liczba * sposobów

Ile tego jest? WRACAMY! Donald Knuth 1938 0 1 2 0 0 1 0 3 1 0 0 1 0 1 dowolnie na sposobów

Ile tego jest? Donald Knuth 1938

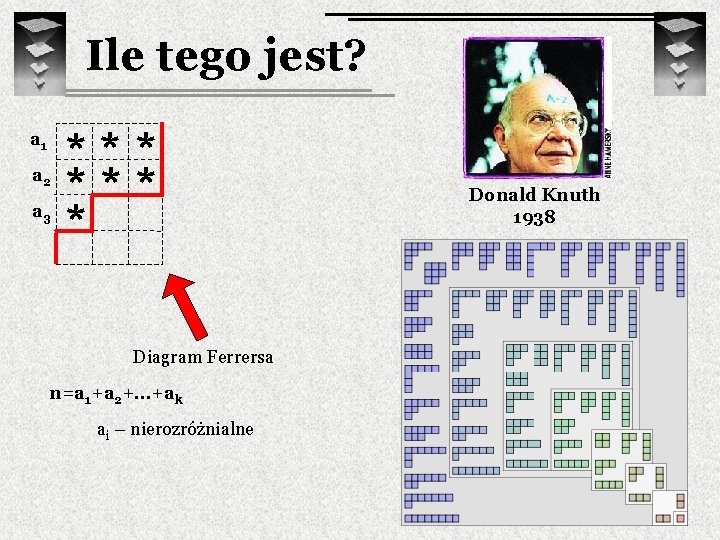
Ile tego jest? a 1 a 2 a 3 *** * Diagram Ferrersa n=a 1+a 2+…+ak ai – nierozróżnialne Donald Knuth 1938

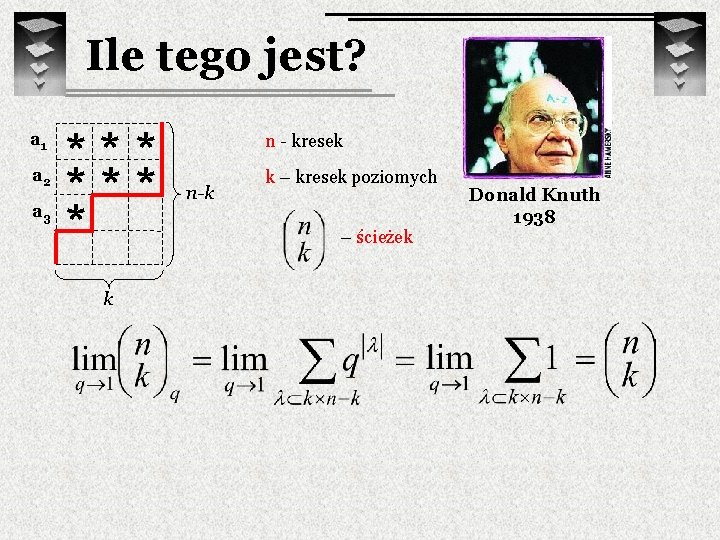
Ile tego jest? a 1 a 2 a 3 *** * k n - kresek n-k k – kresek poziomych – ścieżek Donald Knuth 1938

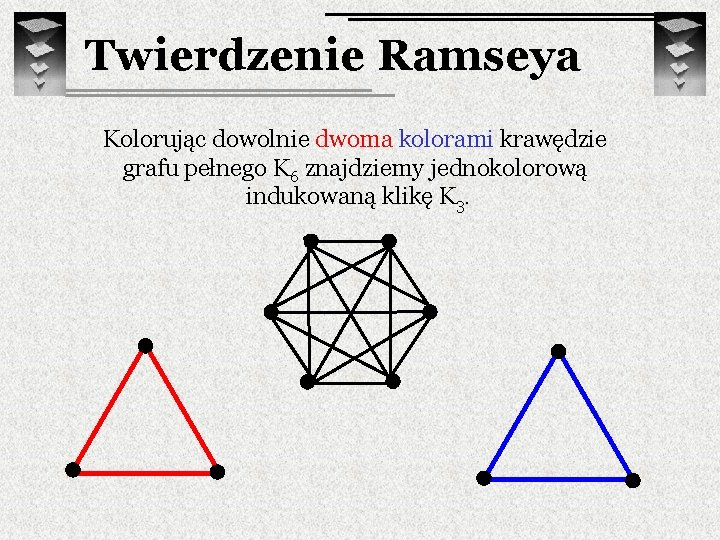
Twierdzenie Ramseya Kolorując dowolnie dwoma kolorami krawędzie grafu pełnego K 6 znajdziemy jednokolorową indukowaną klikę K 3.

Twierdzenie Ramseya

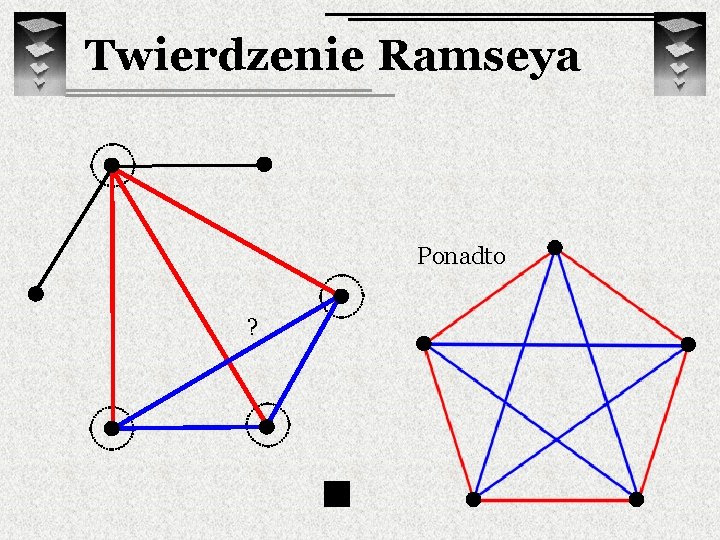
Twierdzenie Ramseya Ponadto ?

Twierdzenie Ramseya Dla każego k istnieje taka liczba n, że przy dowolnym dwukolorowaniu krawędzi grafu pełnego Kn znajdziemy jednokolorową indukowaną klikę Kk. Frank Ramsey (1903 – 1930) Najmniejsze takie n oznaczamy przez R(k) (k-ta liczba Ramseya )

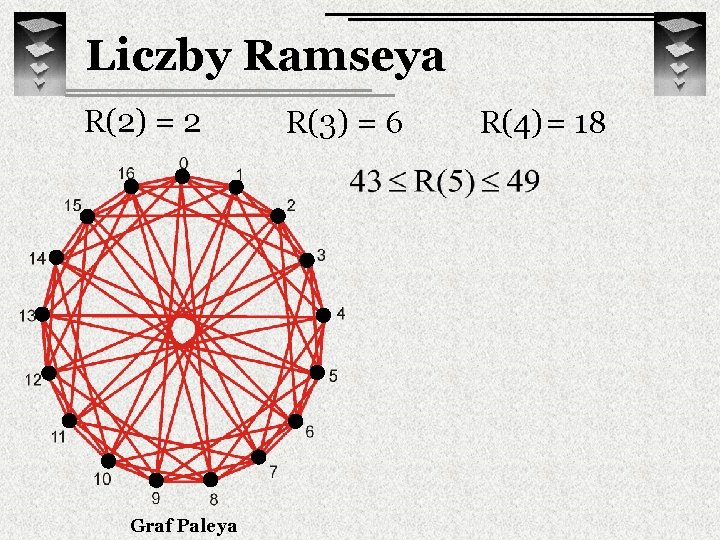
Liczby Ramseya R(2) = 2 Graf Paleya R(3) = 6 R(4) = 18

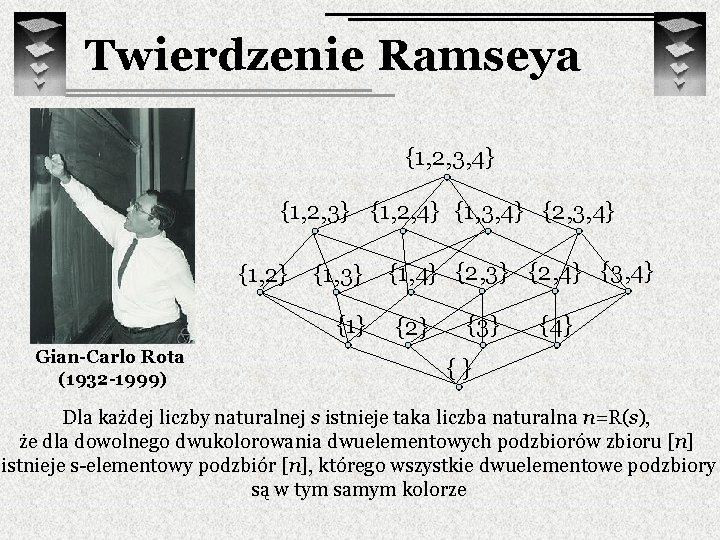
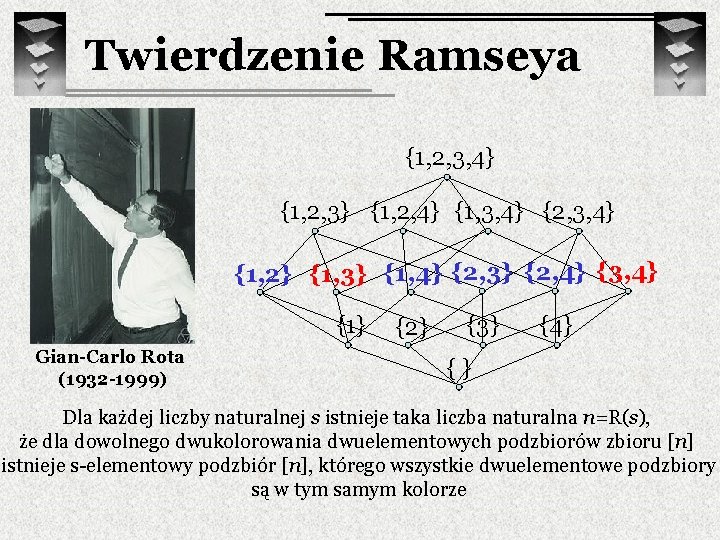
Twierdzenie Ramseya Frank Ramsey (1903 – 1930) Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

Twierdzenie Ramseya {1, 2, 3, 4} {1, 2, 3} {1, 2, 4} {1, 3, 4} {2, 3, 4} {1, 2} {1, 3} {1} Gian-Carlo Rota (1932 -1999) {1, 4} {2, 3} {2, 4} {3, 4} {2} {3} {4} {} Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

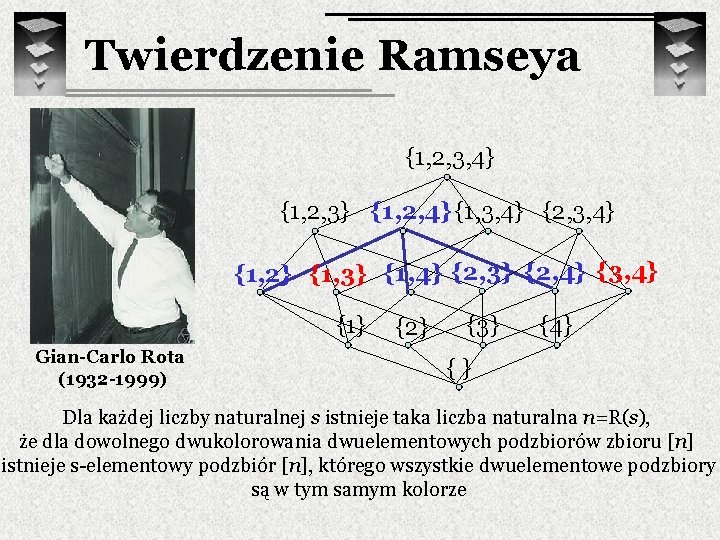
Twierdzenie Ramseya {1, 2, 3, 4} {1, 2, 3} {1, 2, 4} {1, 3, 4} {2, 3, 4} {1, 2} {1, 3} {1, 4} {2, 3} {2, 4} {3, 4} {1} Gian-Carlo Rota (1932 -1999) {2} {3} {4} {} Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

Twierdzenie Ramseya {1, 2, 3, 4} {1, 2, 3} {1, 2, 4}{1, 3, 4} {2, 3, 4} {1, 2} {1, 3} {1, 4} {2, 3} {2, 4} {3, 4} {1} Gian-Carlo Rota (1932 -1999) {2} {3} {4} {} Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

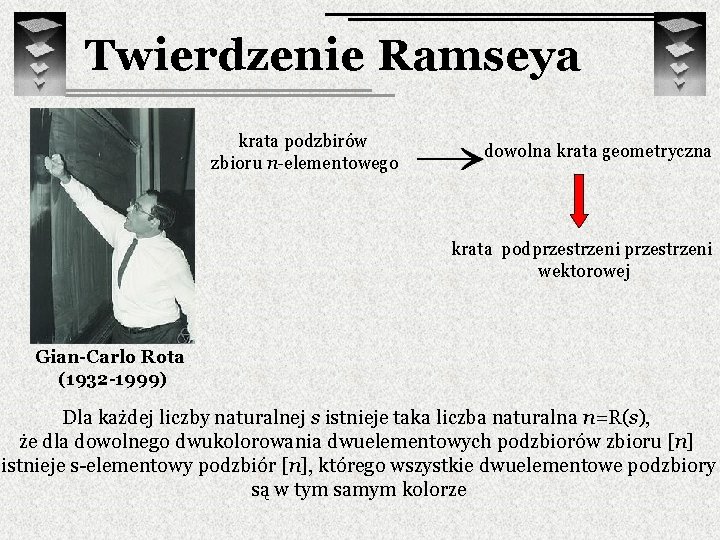
Twierdzenie Ramseya krata podzbirów zbioru n-elementowego dowolna krata geometryczna krata podprzestrzeni wektorowej Gian-Carlo Rota (1932 -1999) Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

Twierdzenie Ramseya krata podzbirów zbioru n-elementowego dowolna krata geometryczna krata podprzestrzeni wektorowej Gian-Carlo Rota (1932 -1999) Dla każdej liczby naturalnej s istnieje taka liczba naturalna n=R(s), że dla dowolnego dwukolorowania dwuelementowych podzbiorów zbioru [n] istnieje s-elementowy podzbiór [n], którego wszystkie dwuelementowe podzbiory są w tym samym kolorze

Twierdzenie Ramseya

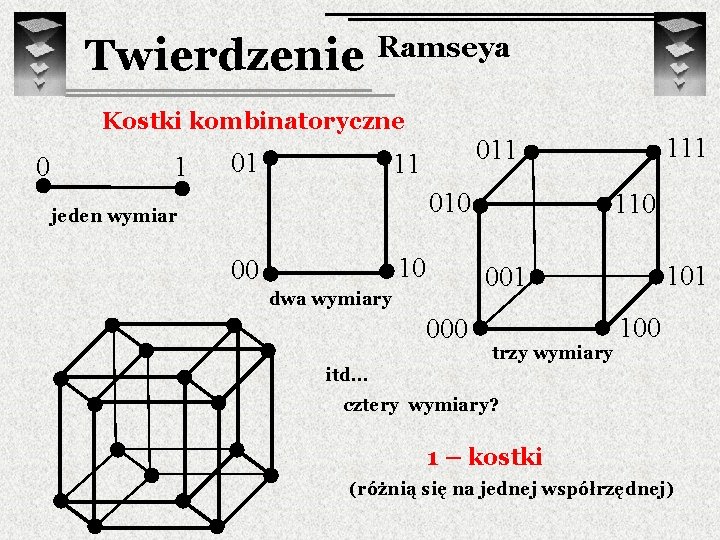
Twierdzenie Ramseya Kostki kombinatoryczne 0 1 01 11 010 jeden wymiar 10 00 111 011 110 101 001 dwa wymiary 000 trzy wymiary 100 itd… cztery wymiary? 1 – kostki (różnią się na jednej współrzędnej)

Twierdzenie Ramseya Dla dowolnych liczb naturalnych k, s, t istnieje taka liczba naturalna n, że dla dowolnego dwukolorowania k-kostek w przestrzeni n-wymiarowej zawsze znajdziemy czerwoną s-kostkę, lub niebieską t-kostkę.

Twierdzenie Ramseya Nagroda Pólyi 1971

Twierdzenie Ramseya Dla dowolnych liczb naturalnych s, t, k istnieje taka liczba naturalna n, że dla dowolnego k-kolorowania t-wymiarowych podprzestrzeni przestezeni n-wymiarowej znajdziemy s-wymiarową przestrzeń, której wszystkie t-wymiarowe podprzestrzenie są jednobarwne.

Liczby Ramseya Jak to szacować? Dla dowolnych liczb naturalnych s, t, k istnieje taka liczba naturalna n, że dla dowolnego k-kolorowania t-wymiarowych podprzestrzeni przestezeni n-wymiarowej znajdziemy s-wymiarową przestrzeń, której wszystkie t-wymiarowe podprzestrzenie są jednobarwne.

Liczby Ramseya Jak to szacować? Największa liczba na świecie

Jak być innym Kwadraty łacińskie 1 2 3 4

Jak być innym Kwadraty łacińskie 1 4 3 2 2 1 4 3 3 2 1 4 4 3 2 1 Leonard Euler (1707 – 1783) Ronald Fisher (1890 -1962) i tablica-okno ku jego pamięci Caius College w Cambridge

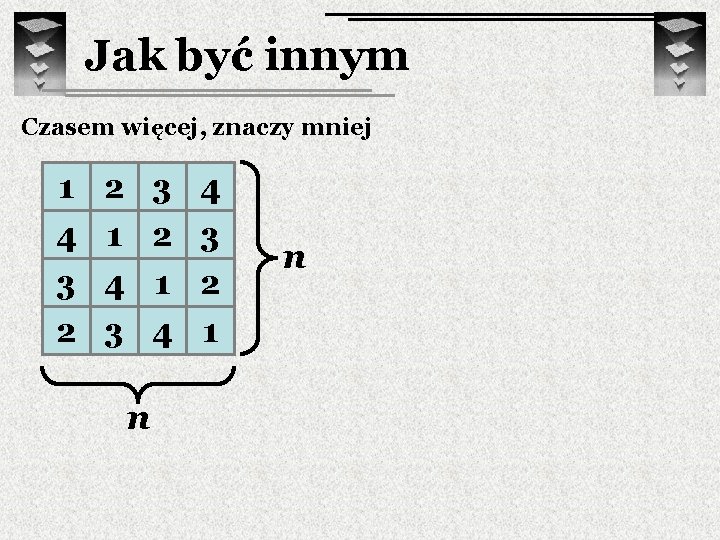
Jak być innym Czasem więcej, znaczy mniej 1 4 3 2 2 1 4 3 3 2 1 4 n 4 3 2 1 n

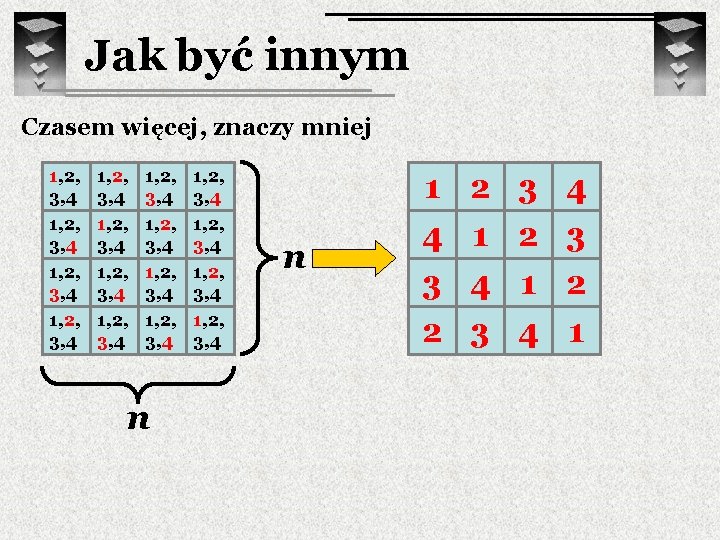
Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 4 1, 2, 3, 4 n 1, 2, 3, 4 n 1 4 3 2 2 1 4 3 3 2 1 4 4 3 2 1

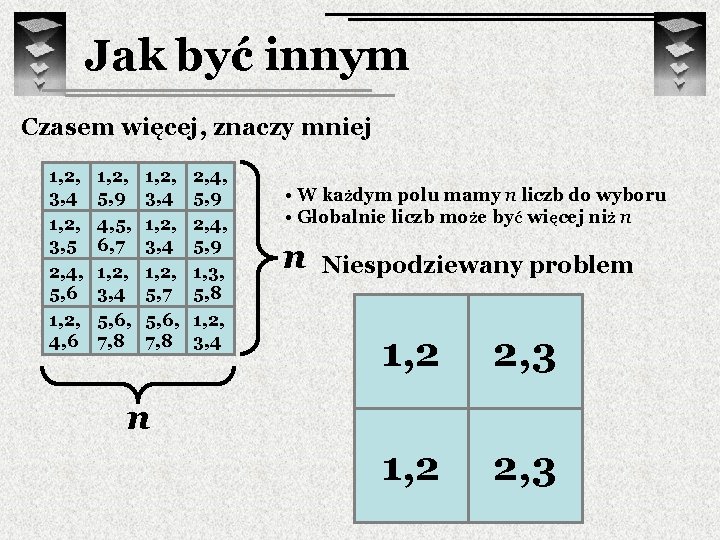
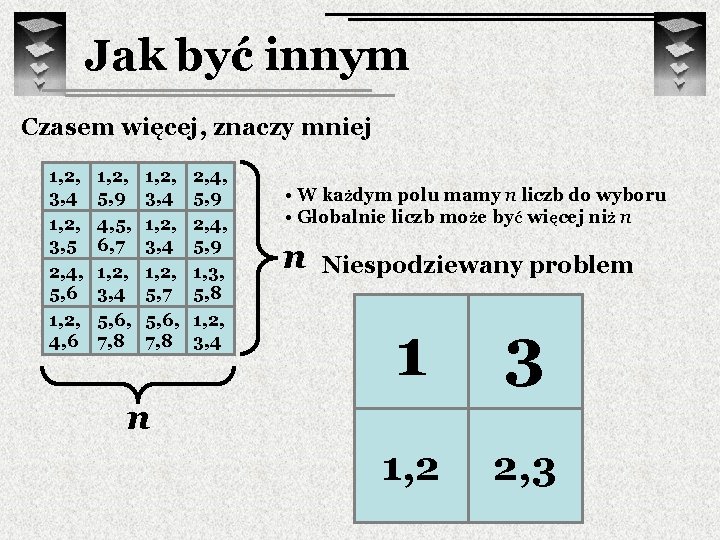
Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 5 2, 4, 5, 6 1, 2, 4, 6 1, 2, 5, 9 4, 5, 6, 7 1, 2, 3, 4 5, 6, 7, 8 1, 2, 3, 4 1, 2, 5, 7 5, 6, 7, 8 2, 4, 5, 9 1, 3, 5, 8 1, 2, 3, 4 • W każdym polu mamy n liczb do wyboru • Globalnie liczb może być więcej niż n n Niespodziewany problem 1, 2 2, 3 n

Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 5 2, 4, 5, 6 1, 2, 4, 6 1, 2, 5, 9 4, 5, 6, 7 1, 2, 3, 4 5, 6, 7, 8 1, 2, 3, 4 1, 2, 5, 7 5, 6, 7, 8 2, 4, 5, 9 1, 3, 5, 8 1, 2, 3, 4 • W każdym polu mamy n liczb do wyboru • Globalnie liczb może być więcej niż n n Niespodziewany problem 1 3 1, 2 2, 3 n

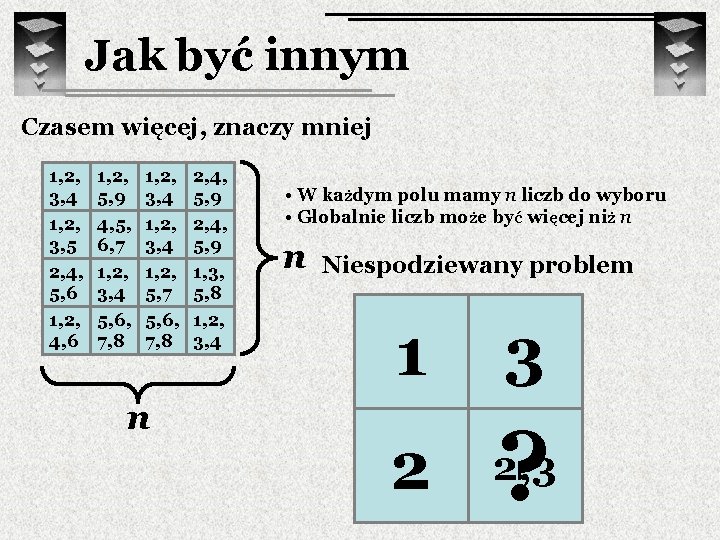
Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 5 2, 4, 5, 6 1, 2, 4, 6 1, 2, 5, 9 4, 5, 6, 7 1, 2, 3, 4 5, 6, 7, 8 1, 2, 3, 4 1, 2, 5, 7 5, 6, 7, 8 n 2, 4, 5, 9 1, 3, 5, 8 1, 2, 3, 4 • W każdym polu mamy n liczb do wyboru • Globalnie liczb może być więcej niż n n Niespodziewany problem 1 3 2 2, 3 ?

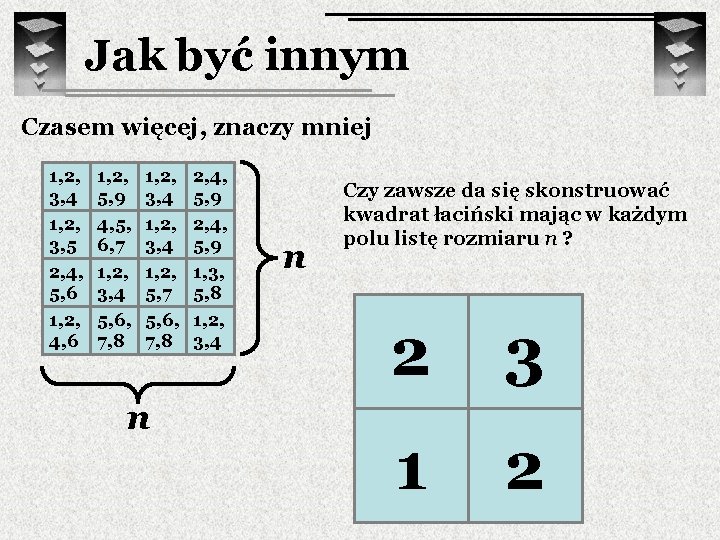
Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 5 2, 4, 5, 6 1, 2, 4, 6 1, 2, 5, 9 4, 5, 6, 7 1, 2, 3, 4 5, 6, 7, 8 1, 2, 3, 4 1, 2, 5, 7 5, 6, 7, 8 n 2, 4, 5, 9 1, 3, 5, 8 1, 2, 3, 4 n Czy zawsze da się skonstruować kwadrat łaciński mając w każdym polu listę rozmiaru n ? 1, 2 2 1 2, 3 1, 2 3 ? 2

Jak być innym Czasem więcej, znaczy mniej 1, 2, 3, 4 1, 2, 3, 5 2, 4, 5, 6 1, 2, 4, 6 1, 2, 5, 9 4, 5, 6, 7 1, 2, 3, 4 5, 6, 7, 8 1, 2, 3, 4 1, 2, 5, 7 5, 6, 7, 8 2, 4, 5, 9 1, 3, 5, 8 1, 2, 3, 4 n Hipoteza Dinitza (1978) Czy zawsze da się skonstruować kwadrat łaciński mając w każdym polu listę rozmiaru n ? TAK! 1994 n Jeff Dinitz - Fred Galvin

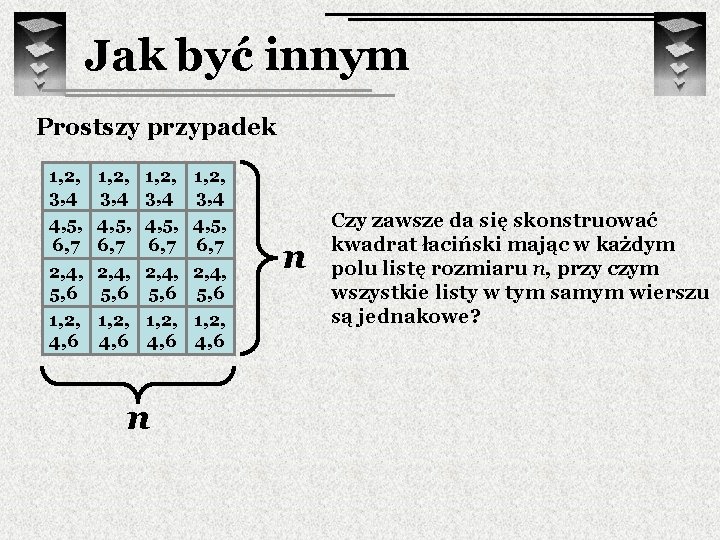
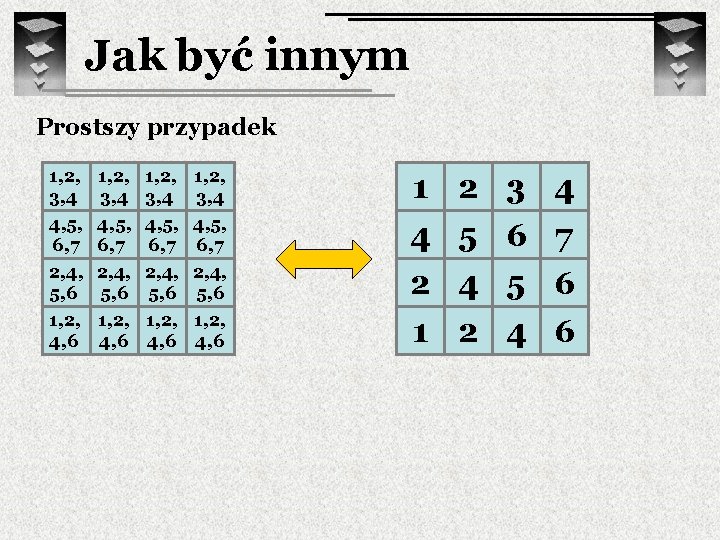
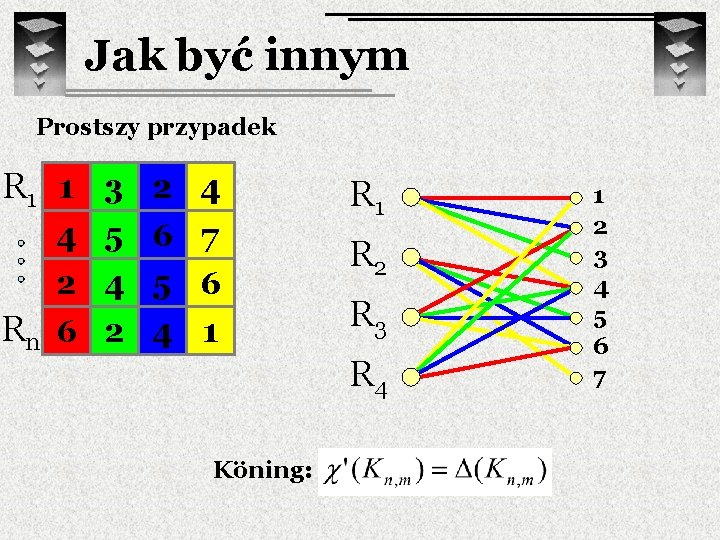
Jak być innym Prostszy przypadek 1, 2, 3, 4 4, 5, 6, 7 2, 4, 5, 6 1, 2, 4, 6 n Czy zawsze da się skonstruować kwadrat łaciński mając w każdym polu listę rozmiaru n, przy czym wszystkie listy w tym samym wierszu są jednakowe?

Jak być innym Prostszy przypadek 1, 2, 3, 4 4, 5, 6, 7 2, 4, 5, 6 1, 2, 4, 6 1 4 2 1 2 5 4 2 3 6 5 4 4 7 6 6

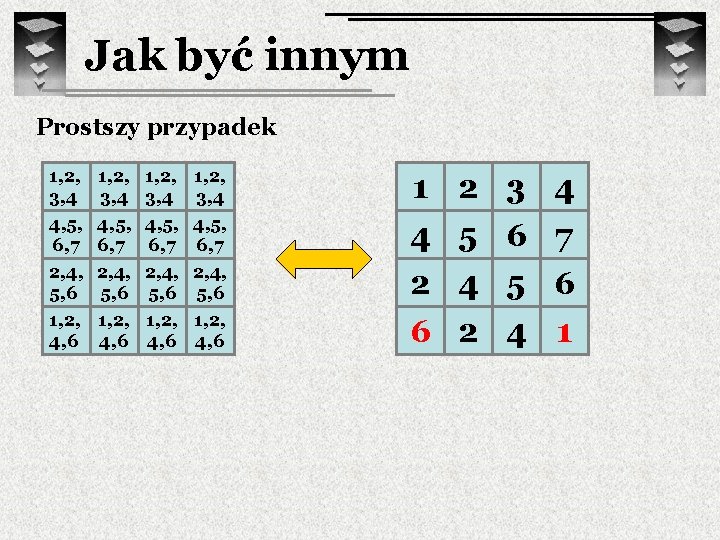
Jak być innym Prostszy przypadek 1, 2, 3, 4 4, 5, 6, 7 2, 4, 5, 6 1, 2, 4, 6 1 4 2 6 2 5 4 2 3 6 5 4 4 7 6 1

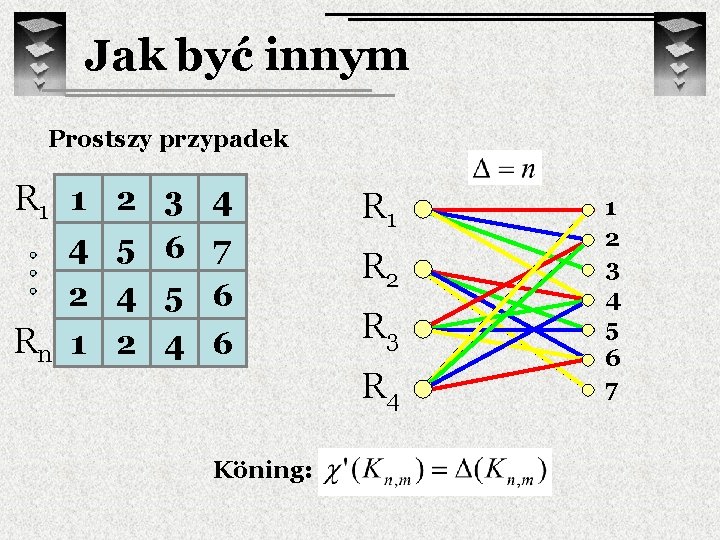
Jak być innym Prostszy przypadek R 1 1 2 3 4 R 1 4 5 6 7 2 4 5 6 Rn 1 2 4 6 R 2 R 3 R 4. . Koning: 1 2 3 4 5 6 7

Jak być innym Prostszy przypadek R 1 1 2 3 4 R 1 4 5 6 7 2 4 5 6 Rn 1 2 4 6 R 2 R 3 R 4. . Koning: 1 2 3 4 5 6 7

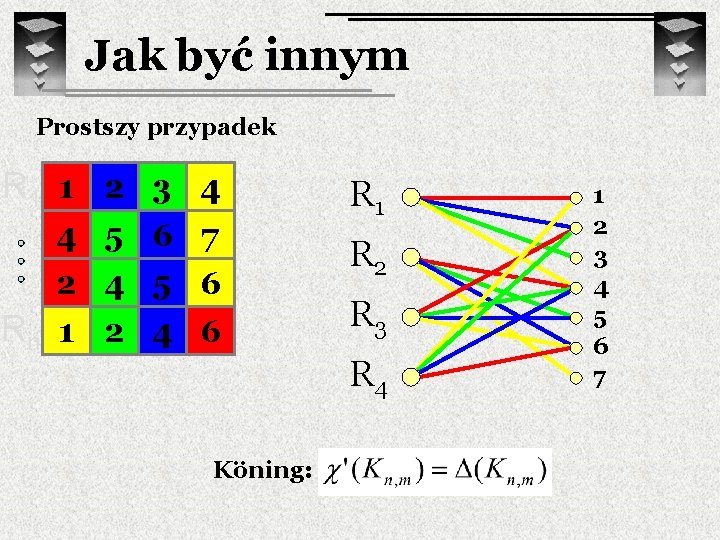
Jak być innym Prostszy przypadek R 1 1 3 2 4 R 1 4 5 6 7 2 4 5 6 Rn 6 2 4 1 R 2 R 3 R 4. . Koning: 1 2 3 4 5 6 7

Jak być niezależnym V – n wymiarowa przestrzeń wektorowa B 1 Bn Bi- bazy przestrzeni V Hipoteza: Da się przepermutować elementy w każdym wierszu w taki sposób, żeby w każdej kolumnie otrzymać bazę V

Jak być niezależnym V – n wymiarowa przestrzeń wektorowa Bi- bazy przestrzeni V B 1 Hipoteza: Da się przepermutować elementy w każdym wierszu w taki sposób, żeby w każdej kolumnie otrzymać bazę V Bn C 1 Cn bazy? Gian-Carlo Rota (1932 -1999)

L 1 nxn [n] 2 3 4 4 1 2 3 4 3 2 1 L – parzysty, jeżeli L – nieparzysty, jeżeli

Jak być niezależnym L nxn [n] 1 2 3 4 4 1 2 3 3 4 1 2 2 3 4 1 le(n)– liczba parzystych kwadratów łacińskich rozmiaru n lo(n)– liczba nieparzystych kwadratów łacińskich rozmiaru n n - nieparzyste Kwadrat nieparzysty otrzymujemy z parzystego (i odwrotnie) zamieniając miejscami dwa wiersze, lub dwie kolumny.

Jak być niezależnym L nxn [n] 1 2 3 4 4 1 2 3 3 4 1 2 2 3 4 1 Hipoteza: Dla parzystych n liczba parzystych kwadratów łacińskich rozmiaru n jest różna od liczby nieparzystych kwadratów łacińskich rozmiaru n. Noga Alon Michael Tarsi

Jak być niezależnym Hipoteza Alona - Tarsiego Hipoteza Roty

Jak być niezależnym Jest prawdziwa: Dla n=2, 3, 4, 6, 8 - Marini Obecnie dla n<26 Dla n=p+1 (p-liczba pierwsza) – A. A. Drisko Hipoteza Alona-Tarsiego Dla n=p-1 (p-liczba pierwsza) – D. G. Glynn Słabsza wersja: B 1 V – n wymiarowa przestrzeń wektorowa Bi- bazy przestrzeni V Możemy tak spermutować elementy w wierszach, żeby kolumny były zbiorami niezależnymi, jeżeli: Bk - J. Geelen, K. Webb

Dziękuję za uwagę