Unit 5 Regression Regression line line that minimizes











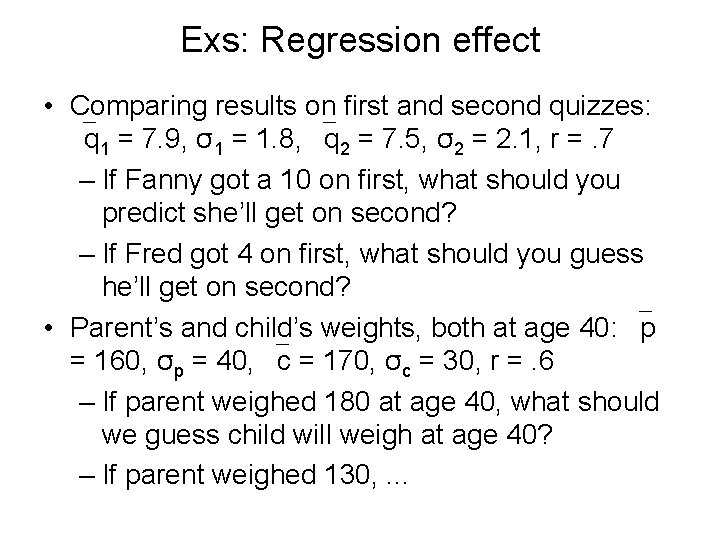


















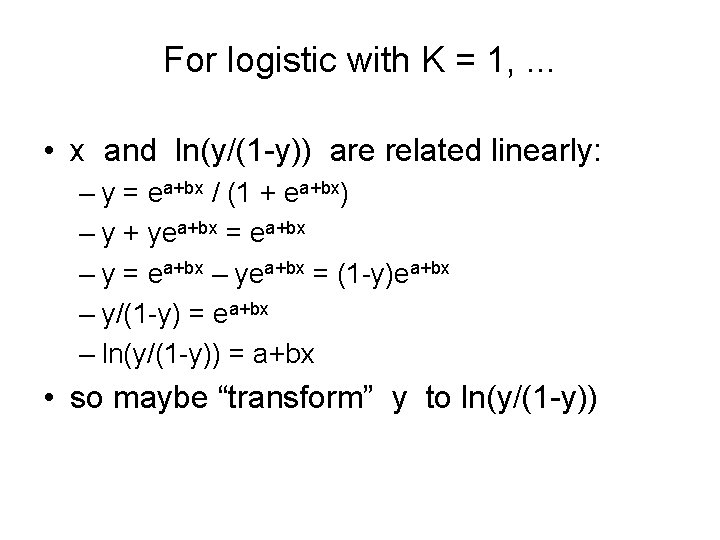

- Slides: 39

Unit 5: Regression

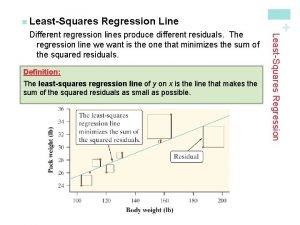
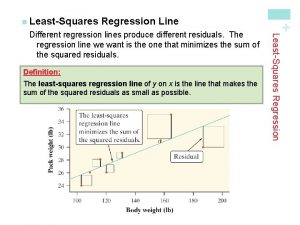
Regression line • line that minimizes sum of squares of vertical distances from data pts (“residuals” or “residues”) • goes through “pt of avgs” ( x , y ) with slope b = r (σy / σx) – by pt-slope: y - y = r (σy / σx)(x - x ) – [so (y-)intercept is y – b x ]


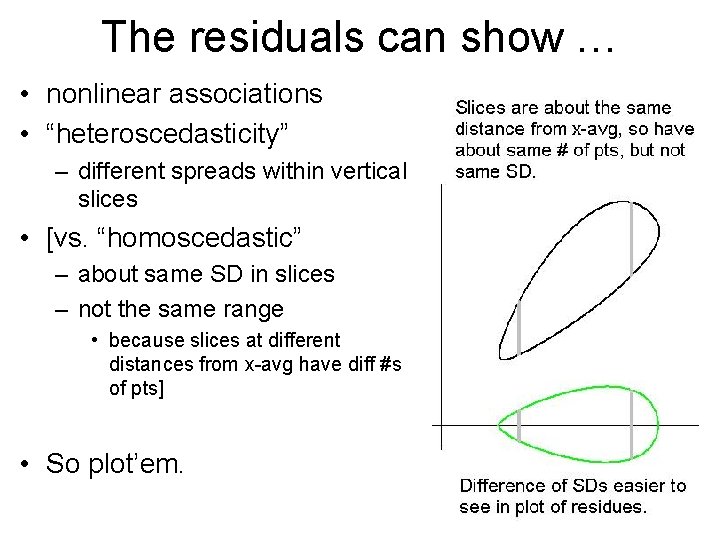
The residuals can show … • nonlinear associations • “heteroscedasticity” – different spreads within vertical slices • [vs. “homoscedastic” – about same SD in slices – not the same range • because slices at different distances from x-avg have diff #s of pts] • So plot’em.

Psych Dept’s version • Regression line is zy = r zx – i. e. , change in x by 1 std unit changes y by the fraction r std unit. • Algebraically equivalent: – (y - y) / σy = r (x - x ) / σx – y - y = r (σy / σx)(x - x )


Projecting y from x with regression • (In business, regression line is “trendline”) • Ex: Cups of coffee and tea drunk daily by CU students. – c = 3, σc = 1, t = 2. 5, σt =. 7, r = -. 4 – If a student drinks 2 coffee, guess how many tea she drinks. • Sol 1: Regr line t - 2. 5 = -. 4(. 7/1)(c - 3), so when c = 2, t = -. 28(2 -3)+2. 5 ≈ 2. 8 • Sol 2: c = 2 in std units is (2 -3)/1 = -1, so project t in std units as -. 4(-1) =. 4, or in cups, . 4(. 7)+2. 5 ≈ 2. 8.

Predictions using regression (II) • Ex: Baldness study, avg # hair (in 10 Ks) is 40, σ = 15; ages avg 36, σ = 20; r = -0. 3. Eqn of regr line? Guess # hair for someone of age 45. . with age 21. • Ex: Admissions Dept guesses 1 st sem GPA (avg 2. 5, σ = 1) from SAT (avg 1200, σ = 200); r = 0. 3. Guess (backward!) SAT for student with 1 st sem GPA 3. 2.

There are 2 regression lines! • Order of variables is now important: • Projecting (guessing) y from x : described above – “regression line of y on x” • Projecting (guessing) x from y : similar formula, but reversing x and y – “regression line of x on y” – graph of this line is more vertical (closer to vertical axis), even more than SD-line – Don’t use the first eqn, substitute y-value and solve for x!


Ex: Which regr line? • College admissions officer uses SAT scores to project 1 st sem GPA: s = 1200, σs = 200, g = 2. 5, σg = 1, r =. 3 – Regression line for g on s: g – 2. 5 =. 3(1/200)(s – 1200) or g =. 0015 s +. 7 • If a student has 1 st sem GPA of 3. 2, what should we guess her SAT is? – (3. 2 -. 7)/. 0015 ≈ 1670? – 1242, from other regr line?

Regression effect • (0<r<1) If we look only at x-values above x, the corresponding y-values will be lower (i. e. , closer to y), –. . . while if we look only at x-values below x, the corresponding y-values will be higher. • Sir Francis Galton (1822 -1911): “regression to mediocrity” • Hence “regression”, though not much is “going back”. • The “regression fallacy” is to attribute this to anything other than imperfect regression. – E. g. , “sophomore slump”
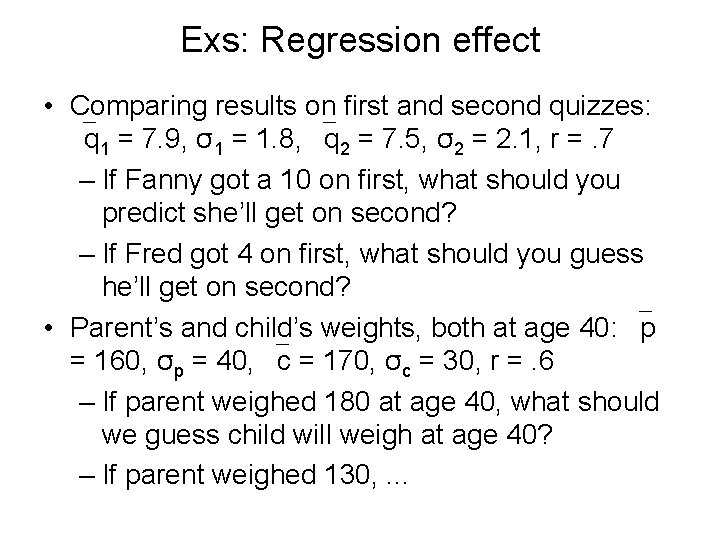
Exs: Regression effect • Comparing results on first and second quizzes: q 1 = 7. 9, σ1 = 1. 8, q 2 = 7. 5, σ2 = 2. 1, r =. 7 – If Fanny got a 10 on first, what should you predict she’ll get on second? – If Fred got 4 on first, what should you guess he’ll get on second? • Parent’s and child’s weights, both at age 40: p = 160, σp = 40, c = 170, σc = 30, r =. 6 – If parent weighed 180 at age 40, what should we guess child will weigh at age 40? – If parent weighed 130, . . .

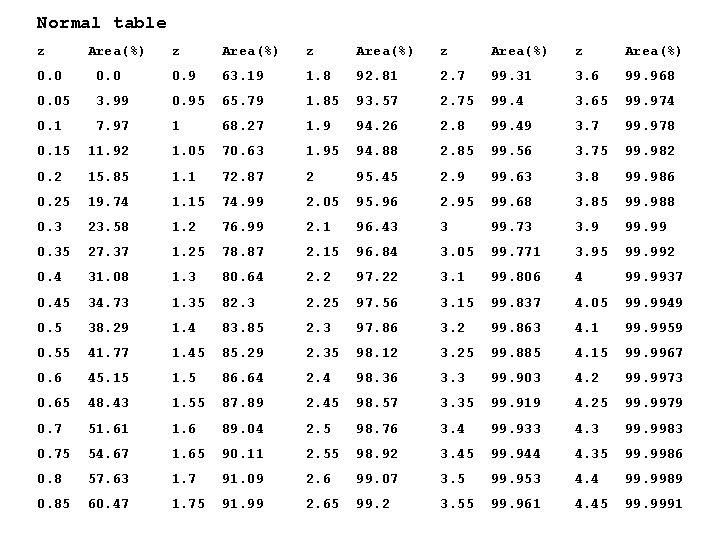
Projecting %iles with regression • (Assumes both variables are normal, . . . • but avgs and std devs aren’t needed) • Suppose # of hairs on a man’s head and his IQ have r = -. 7: (a) If he is at 80 th %ile in # hairs, about what is his IQ %ile? (b) If he is at 10 th %ile in IQ, about what is hair %ile?

Normal table z Area(%) z Area(%) 0. 0 0. 9 63. 19 1. 8 92. 81 2. 7 99. 31 3. 6 99. 968 0. 05 3. 99 0. 95 65. 79 1. 85 93. 57 2. 75 99. 4 3. 65 99. 974 0. 1 7. 97 1 68. 27 1. 9 94. 26 2. 8 99. 49 3. 7 99. 978 0. 15 11. 92 1. 05 70. 63 1. 95 94. 88 2. 85 99. 56 3. 75 99. 982 0. 2 15. 85 1. 1 72. 87 2 95. 45 2. 9 99. 63 3. 8 99. 986 0. 25 19. 74 1. 15 74. 99 2. 05 95. 96 2. 95 99. 68 3. 85 99. 988 0. 3 23. 58 1. 2 76. 99 2. 1 96. 43 3 99. 73 3. 9 99. 99 0. 35 27. 37 1. 25 78. 87 2. 15 96. 84 3. 05 99. 771 3. 95 99. 992 0. 4 31. 08 1. 3 80. 64 2. 2 97. 22 3. 1 99. 806 4 99. 9937 0. 45 34. 73 1. 35 82. 3 2. 25 97. 56 3. 15 99. 837 4. 05 99. 9949 0. 5 38. 29 1. 4 83. 85 2. 3 97. 86 3. 2 99. 863 4. 1 99. 9959 0. 55 41. 77 1. 45 85. 29 2. 35 98. 12 3. 25 99. 885 4. 15 99. 9967 0. 6 45. 15 1. 5 86. 64 2. 4 98. 36 3. 3 99. 903 4. 2 99. 9973 0. 65 48. 43 1. 55 87. 89 2. 45 98. 57 3. 35 99. 919 4. 25 99. 9979 0. 7 51. 61 1. 6 89. 04 2. 5 98. 76 3. 4 99. 933 4. 3 99. 9983 0. 75 54. 67 1. 65 90. 11 2. 55 98. 92 3. 45 99. 944 4. 35 99. 9986 0. 8 57. 63 1. 7 91. 09 2. 6 99. 07 3. 5 99. 953 4. 4 99. 9989 0. 85 60. 47 1. 75 91. 99 2. 65 99. 2 3. 55 99. 961 4. 45 99. 9991

RMS error for regression • This is the square root of the average of the squares of the residues, i. e. , the differences between the y-values of the data points and the y-values on the regression line (predictions) at the same x-values. • Also called “residual standard error” • Regr line was chosen to minimize this value • Using formula for regr line (and a lot of algebra), we find this is just σy √[1 -r 2] – Note formula uses the σ of the variable we are trying to project

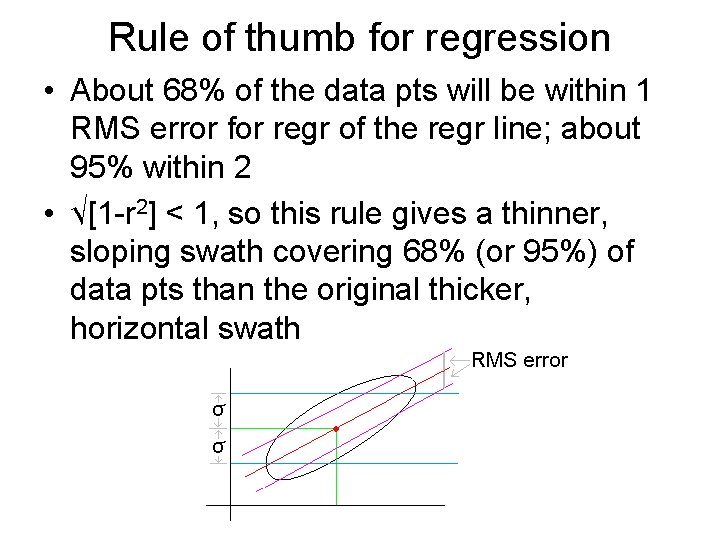
Rule of thumb for regression • About 68% of the data pts will be within 1 RMS error for regr of the regr line; about 95% within 2 • √[1 -r 2] < 1, so this rule gives a thinner, sloping swath covering 68% (or 95%) of data pts than the original thicker, horizontal swath

If the data is homoscedastic, • i. e. , std devs in vertical slices of data are roughly equal throughout • (text calls this “football-shaped”, but “cigar-shaped” would be just as sensible, depending on relative sizes of σx , σy ), . . . • then RMS error for regr is this common σ. • Ex: SAT scores vs. 1 st sem GPA: s = 1200, σs = 200, g = 2. 5, σg = 1, r =. 3 – – Project GPA if SAT is 1300 by regr: 2. 65 Likely to be off by RMS error: 1√[1 -. 32] ≈. 95 If GPA is 1. 8, guess SAT by regr: 1158 Likely to be off by 200√[1 -. 32] ≈ 191

Normal approx within a vertical slice (? ? ? ) • Ex (cntd): SAT scores vs. 1 st sem GPA: s = 1200, σs = 200, g = 2. 5, σg = 1, r =. 3 • (and assume homoscedastic): • Suppose a student has a 1300 SAT and a 3. 7 GPA. What %ile does that make her GPA among the students who got 1300 SATs? – In that group (like all the other vertical slices), best guess for σ is RMS error for regr, ≈. 95, – and by regr, best guess for avg within slice is 2. 65, – so in slice, her GPA z-value is (3. 7 -2. 65)/. 95 ≈ 1. 10 – and by normal table, that’s 86 th %ile

Warning on regression: • Don’t extrapolate. • Ex: Grade inflation at CU: GPA avg in F 1993 was 2. 91, increasing 0. 008/sem (r = 0. 93). By S 2058, avg GPA will be 4. 00. (? )

HERE BE DRAGONS • From this point on in this presentation, the material is not in the text. • In fact, our authors specifically warn against some methods (like transforming data), but the methods are commonly used. • This material will not be on an exam, . . . • but multivariate regression is used in Midterm Project II.

What does r 2 measure? • Answer: It says how much better for predicting y is using regr line (i. e. , using the y-value ŷ on the regression line at that point) than just always using y – Difference of SSE (sum of squares of errors) using avg [i. e. , ∑(y - y)2] vs. SSE using regr [i. e. , sum of squares of residuals ∑(y - ŷ)2], divided by SSE using avg. . . –. . . which = r 2 (see next slide) – so, if r 2 = 0. 4, say, “regression results in a 40% improvement in projection”


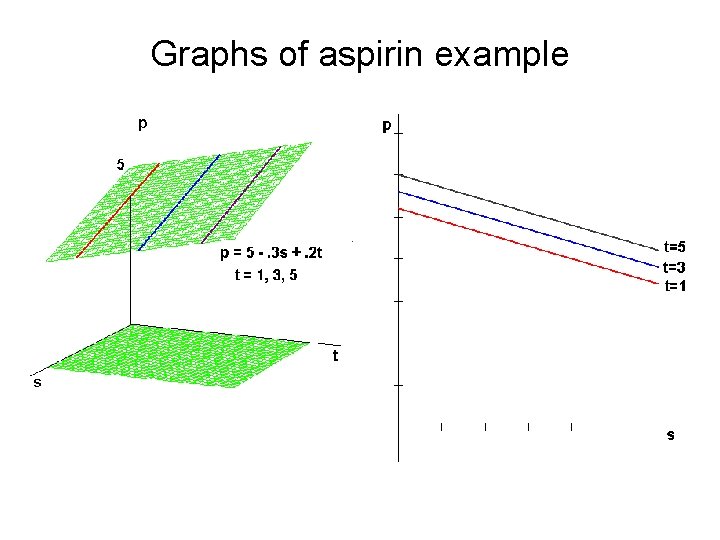
Multiple (linear) regression • If there is more than one explanatory variable (x 1, x 2, x 3 say) and one response variable (y), it may be useful to model it as y = a + b 1 x 1 + b 2 x 2 + b 3 x 3 • Ex: Aspirin is so acidic that it often upsets the stomach, so it is often administered with an antacid -- which limits effect. Suppose the pain, measured by the rating of headache sufferers, is given by p = 5 -. 3 s +. 2 t where s is the aspirin dose and t is the antacid dose.

Graphs of aspirin example

Multiple regression • As with simple regression, there is a (multiple) correlation R (indep of units) that measures how closely the data points (in 3 -space or higher dims) follow a (hyper)plane • (What does the sign mean, because y can go up when x 1 goes up or when x 2 goes down? ) • In this case R 2 is easier to understand (and means the same as before), so it appears in the computer outputs as well • The next page is Excel output from a (fictional) economic multiple. (Bold italics = added)


Polynomial regression • If theory or scatterplot (or plot of residues) suggests a higher-degree polynomial would fit data better than linear regression of y on x , add cols of x 2 (and x 3 and. . . ) and do multiple regression. • Ex of theory: path of projectile under gravity, weight vs. height • Ex of fitting: Boston poverty level vs. property values (Midterm Project I)


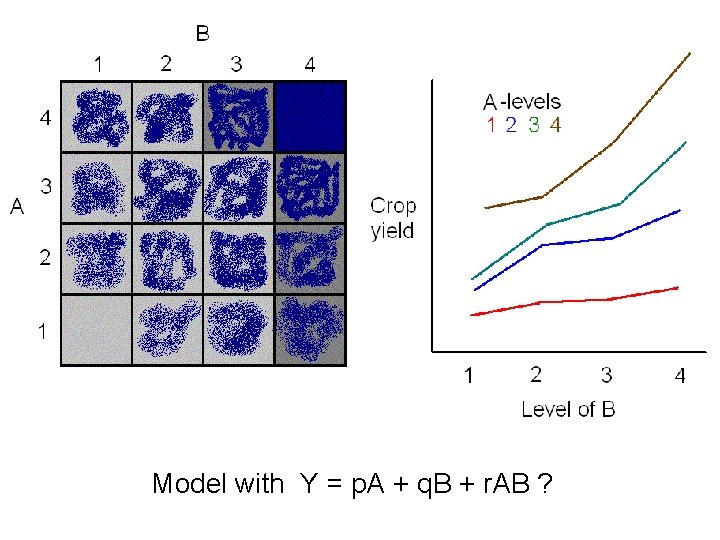
Model with Y = p. A + q. B + r. AB ?

Correlations in multiple regression • If we add more x-variables in an attempt to approximate a y-variable, the absolute R-value (or R 2 -value) cannot go down. – It will probably go up, unless there is no relation at all between the new x-variables and y. • But the correlations between the old x-variables and y may change – may even change sign! – as new x -values are added. – Ex: In the thrown ball example, both t 2 and h go up, at least initially, so without t their correlation is positive. But if we add t , it’s a better determiner of h , and t 2 becomes a negative influence on h, namely in the gravity term.

Curvilinear associations • (Linear) regression, as we have studied it, is built to find the best line approximating data. But sometimes theory, or just a curviness of the data cloud, hint that the equation that best relates the xand y-values is not a line. • In this case, experimenters often “transform” the data, replacing the x-, or y-, or both values by their logs, or their squares, or. . . and use regression on the new data to find slopes and intercepts, which translate to exponents or other constants in equations for the original data • The next few slides are a fast intro to some common forms of equations that might relate variables.

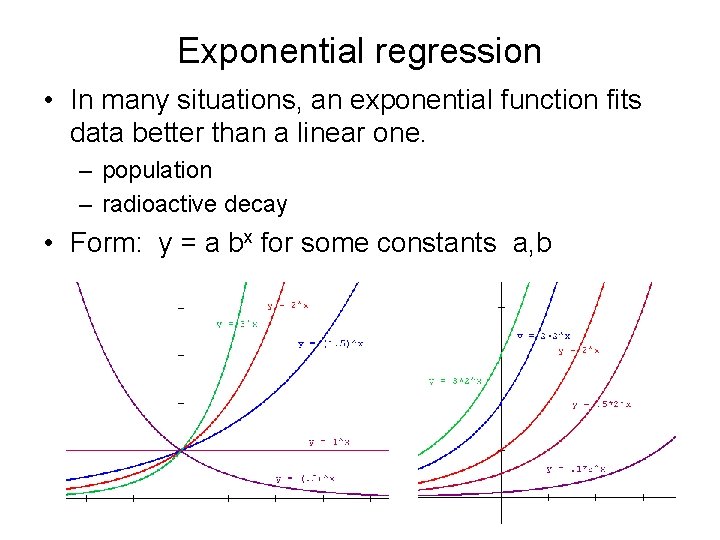
Exponential regression • In many situations, an exponential function fits data better than a linear one. – population – radioactive decay • Form: y = a bx for some constants a, b

Logarithms • • y = bx and x = logb(y) say the same thing From cxcy = cx+y : logc(uv) = logc(u) + logc(v) From (cy)x = cyx : logc(ax) = x logc(a) So y = a bx can be written as logc(y) = logc(a) + x logc(b) • Thus, x and logc(y) are linearly related • So maybe replace (“transform”) y by logc(y) – (Our authors don’t trust this or any other transformation, because any measurement errors, which were originally assumed normally distributed, won’t remain so after the transformation)

Richter

Exp and log notation • e = 2. 71828. . . (more convenient base for calculus reasons) • exp(x) = ex – [Note: ax = (blogb(a))x = bx logb(a) – so switching bases is just a linear change of variable (sorta)] • ln = loge ; log = log 10 , log 2 , . . .

Logistic models • Several applications fit “logistic” models better than linear, exp or log – y = K ea+bx/(1+ea+bx) – For large x , y is close to K • In population models, K is “carrying capacity”, i. e. , max sustainable pop • But y may be proportion p of pop, so K=1 – For large neg x , y is close to 0 • Ex: Smokers: x = # packs/day, p = % who smoke that much and have a cough
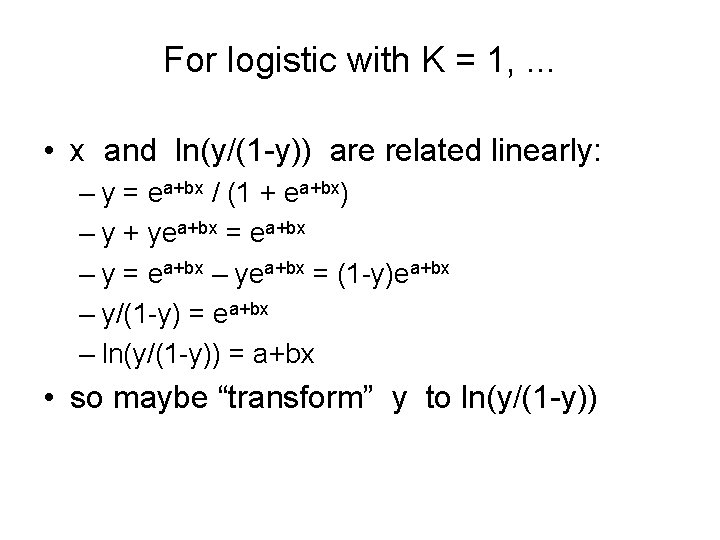
For logistic with K = 1, . . . • x and ln(y/(1 -y)) are related linearly: – y = ea+bx / (1 + ea+bx) – y + yea+bx = ea+bx – yea+bx = (1 -y)ea+bx – y/(1 -y) = ea+bx – ln(y/(1 -y)) = a+bx • so maybe “transform” y to ln(y/(1 -y))

 Ngoại tâm thu thất chùm đôi
Ngoại tâm thu thất chùm đôi Block xoang nhĩ độ 2 type 1
Block xoang nhĩ độ 2 type 1 Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Chiến lược kinh doanh quốc tế của walmart
Chiến lược kinh doanh quốc tế của walmart Tìm vết của mặt phẳng
Tìm vết của mặt phẳng Hãy nói thật ít để làm được nhiều
Hãy nói thật ít để làm được nhiều Tôn thất thuyết là ai
Tôn thất thuyết là ai Gây tê cơ vuông thắt lưng
Gây tê cơ vuông thắt lưng Sau thất bại ở hồ điển triệt
Sau thất bại ở hồ điển triệt Simple and multiple linear regression
Simple and multiple linear regression Linear model regression
Linear model regression Logistic regression vs linear regression
Logistic regression vs linear regression Logistic regression vs linear regression
Logistic regression vs linear regression Unit 10, unit 10 review tests, unit 10 general test
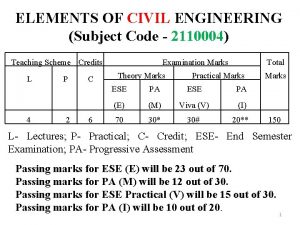
Unit 10, unit 10 review tests, unit 10 general test 66454 subject code
66454 subject code Least squares regression line definition
Least squares regression line definition How to find least squares regression line on statcrunch
How to find least squares regression line on statcrunch Median median regression line
Median median regression line How to find lsrl
How to find lsrl Www.whfreeman/tps5e
Www.whfreeman/tps5e State the properties of least square estimators
State the properties of least square estimators Properties of regression line
Properties of regression line Least squares regression line definition
Least squares regression line definition Least squares regression line minitab
Least squares regression line minitab Unit surplus dan unit defisit
Unit surplus dan unit defisit Hyp opp adj
Hyp opp adj English system conversion
English system conversion Algebra 2 unit 1 practice test
Algebra 2 unit 1 practice test Unit cost rekam medis
Unit cost rekam medis Unit process and unit operation
Unit process and unit operation What is unit operation and unit process
What is unit operation and unit process Kerangka konseptual akuntansi pemerintahan
Kerangka konseptual akuntansi pemerintahan Line matching unit
Line matching unit Ulysses alfred tennyson analysis
Ulysses alfred tennyson analysis Daffodils poem
Daffodils poem Thou blind man's mark ap lit
Thou blind man's mark ap lit A poem of 14 lines
A poem of 14 lines Tajmahal poem
Tajmahal poem Sonnet 60 theme
Sonnet 60 theme