UNIDAD I Nociones preliminares 1 1 Nmeros reales

UNIDAD I Nociones preliminares 1. 1 Números reales 1. 1. 1 Conjunto de números reales y la recta númerica 1. 1. 2 Intervalos y su clasificación 1. 1. 3 Desigualdades y su solución 1. 2 Funciones 1. 2. 1 Dominio y rango de una función 1. 2. 2 Gráficas de funciones 1. 2. 3 Operaciones con funciones 1. 2. 4 Composición de funciones

1. 3 Límite de funciones 1. 3. 1 Concepto de límite de una función 1. 3. 2 Límites laterales 1. 3. 3 Teoremas de límites 1. 3. 4 Límites infinitos 1. 4 Continuidad de funciones 1. 4. 1 Continuidad de una función, análisis gráfico 1. 4. 2 Teoremas de continuidad de funciones 1. 4. 3 Continuidad de una función en un punto y en un intervalo

UNIDAD II Derivada 2. 1 Derivada de una función 2. 1. 1 La derivada como razón de cambio 2. 1. 2 Interpretación geométrica y física de la derivada 2. 2 Cálculo de derivadas 2. 2. 1 Regla general de derivación 2. 2. 2 Estudio y aplicación de las fórmulas de derivación

2. 3 Aplicación de la derivada 2. 3. 1 Concavidad 2. 3. 2 Métodos para la obtención de máximos y mínimos 2. 3. 3 Problemas de aplicación de máximos y mínimos 2. 4 Teoremas de derivación 2. 4. 1 Regla de la cadena 2. 4. 2 Teorema de Rolle y del valor medio

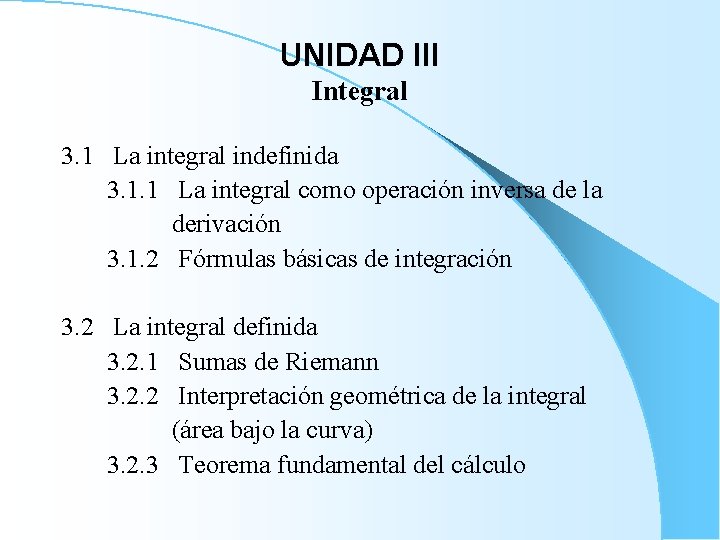
UNIDAD III Integral 3. 1 La integral indefinida 3. 1. 1 La integral como operación inversa de la derivación 3. 1. 2 Fórmulas básicas de integración 3. 2 La integral definida 3. 2. 1 Sumas de Riemann 3. 2. 2 Interpretación geométrica de la integral (área bajo la curva) 3. 2. 3 Teorema fundamental del cálculo

3. 3 Métodos de integración 3. 3. 1 Por sustitución 3. 3. 2 Por sustitución trigonométrica 3. 3. 3 Por racionalización 3. 3. 4 Por partes

Preliminares l. Sistema de números reales l. Desigualdades

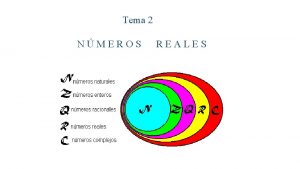
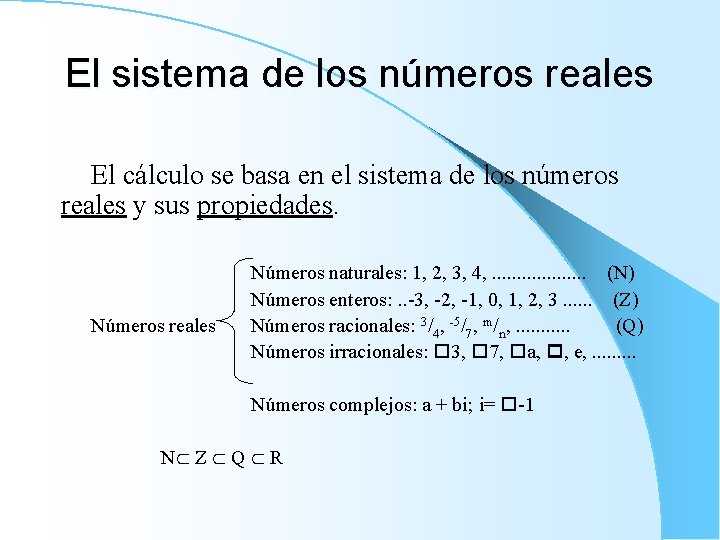
El sistema de los números reales El cálculo se basa en el sistema de los números reales y sus propiedades. Números reales Números naturales: 1, 2, 3, 4, . . (N) Números enteros: . . -3, -2, -1, 0, 1, 2, 3. . . (Z) Números racionales: 3/4, -5/7, m/n, . . . (Q) Números irracionales: 3, 7, a, , e, . . Números complejos: a + bi; i= -1 N Z Q R

Propiedades de campo v Ley conmutativa: x+y=y+x; xy=yx 2+3 = 3+2; 5 = 5 ; (2)(3)=(3)(2) 6 = 6 asociativa: x+(y+z)=(x+y)+z; (xy)z=x(yz) 2 + (3 + 5) = (2+3)+5; 2+8=5+5 10 = 10 v Ley distributiva: (2*3)5=2(3*5) 6 * 5 =2 *15 30 = 30 x(y+z) = xy + xz 2(3 + 5) = 2*3 + 2*5 2 * 8 = 6 + 10 16 = 16 v Elementos neutros: x+0= x 2+0=2 v Inversos: x(1) = x 2*1=2 x+(-x)=0 x(x-1)= 1 2 + (-2)=0 2 (2 -1)= 2(1/2)= 1

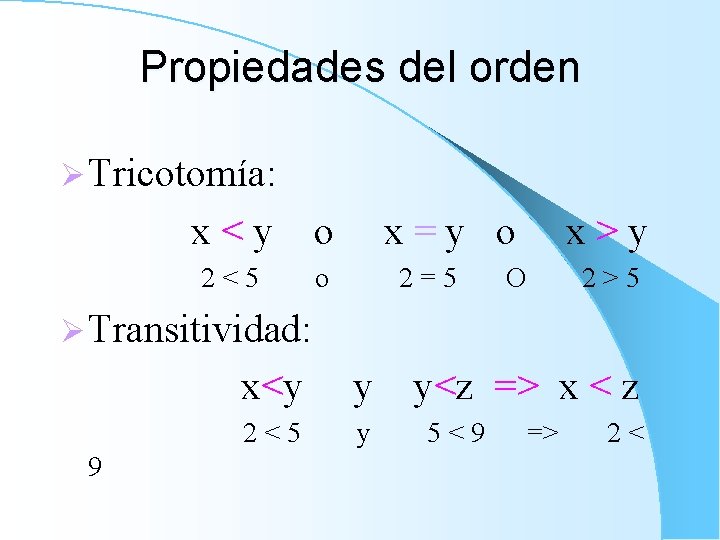
Propiedades del orden Ø Tricotomía: x<y o 2<5 o x=y o 2=5 x>y O 2>5 Ø Transitividad: 9 x<y y 2<5 y y<z => x < z 5<9 => 2<

x<y x+z < y+z 2<5 2+3 < 5+3 5 < 8 Ø Multiplicativa: z > 0 => x < y xz < yz 8 > 0 => 2 < 5 2*8 < 5*8 16 < 40 z < 0 => x < y xz > yz -8 < 0 => 2 < 5 2(-8) > 5(-8) -16 > -40 Ø Aditiva:

Simplifique todo lo que sea posible 1) 2) 3) 4) 5) 6) 7) 4 -3(8 -12)-6 = 2(3 -2(4 -8)) = -4[3(-6+13)-2(5 -9)]= 5[-1(7+12 -16)+4]+2 = 5/ – (1/ +2/ ) = 6 4 3 ¾-(7/12 – 2/9) = 1/ [1/ (1/ -1/ )+1/ ] = 3 2 4 3 6

Ejercicios resueltos 1) 4 -3(8 -12)-6 = 1° se resuelve el paréntesis 4 -3(-4)-6 = El resultado (-4) se multiplica por 3 4+12 -6 = Se suman todos los positivos y los negativos 16 -6 = 10 3) -4[3(-6+13)-2(5 -9)]= 1° se resuelve color verde -4[3(7)-2(-4)]= Se multiplica el paréntesis con su literal -4[21+8]= Se resuelve color lila -4[29]= -116 Se multiplica

5) 5/6 – (1/4+2/3) = Paréntesis ¿? a/b+c/d=(ad+cb)/bd 5/ – (1)(3)+(2)(4)/ Simplificar 6 (4)(3) = 5/ – 3+8/ = 5/ – 11/ 6 12 Igualar denominadores (mcm) 5/ – 11/ = (5/ )(2/ ) – 11/ 2/ =1, x*1=x 6 12 6 2 12 2 10/ – 11/ = – 1/ Mismo denominador (12), 12 12 12 numeradores se suman.

7) 1/3[1/2(1/4 -1/3)+1/6] = 1/ 1/ (1(3)-1(4)/ 1/ ] = [ )+ 3 2 4(3) 6 1/ 1/ (3 -4/ )+1/ ] = [ 3 2 12 6 1/ 1/ (-1/ )+1/ ] = [ 3 2 12 6 1/ [-1/ +1/ ] = 3 24 6 1/ [-1/ +(1/ )(4/ )] = 3 24 6 4 1/ [-1/ +4/ ] = 3 24 24 1/ [3/ ] = 3/ = 1/ 3 24 72 24 9) (5/7+2/9)/(1+1/2) = (5(9)+ 2(7)/7(9))/(2/2+1/2) = (45+14/63)/(3/2) = (59/63)/(3/2) = a/b/c/d= ad / bc (59)(2)/ 118/ = (63)(3) 189 11) 1 - 2/(2 + 3/4) = 1 - 2/(8/4 + 3/4) = 1 - 2/1/(11/4) = 1 – 2(4)/ 1(11) = 11/11 – 8/ = 3/ 11 11

Realice las operaciones indicadas y simplifique a) (2 x-3)(2 x+3)= b) (2 x-3)2= c) (-3 t 2 -t+1)2= d) (2 t-1)3= e) (x 2 -4) / (x-2)= f) (x 2 -x-6)/ (x-3)= g) (x 3 -8) / (2 x-4) = h) (2 x-2 x 2) / (x 3 -2 x 2+x)=

a) (2 x-3)(2 x+3)= (2 x)2 -(3)2= 4 x 2 -9 b) (a+b)2 = a 2+2 ab+b 2 (2 x-3)2 = (2 x)2+2(2 x)(-3)+(-3)2 =4 x 2 -12 x+9 l (a+b+c)2= a 2+b 2+c 2+2 ab+2 ac+2 bc (3 t 2 -t+1)2 = (3 t 2)2+(-t)2+(1)2+2(3 t 2)(-t)+2(3 t 2)(1)+2(-t)(1) = 9 t 4 + t 2 + 1 - 6 t 3 + 6 t 2 - 2 t = 9 t 4 - 6 t 3 + 7 t 2 - 2 t + 1

d) (a+b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 (2 t-1)3= (2 t)3 + 3(2 t)2(-1) + 3(2 t)(-1)2 + (-1)3 = 8 t 3 - 3(4 t 2) + 3(2 t)(1) -1 = 8 t 3 - 12 t 2 + 6 t – 1 e) (x 2 -4)/(x-2)= Factorizar el numerador. Buscar dos # que (a)(b) den – 4 y (a)+(b) den 0. (x 2+0 x-4) (x-2)(x+2)/(x-2)= Como (x-2) se encuentra en el numerador y en el denominador, se cancela. x+2 f) (x 2 -1 x-6)/(x-3)= (a)(b)= -6 Y (a)+(b)= -1 (x+2)(x-3)/(x-3)= (-3)(2)= -6 Y (-3)+(2)= -1 x+2

Desigualdades Una expresión algebraica con cualquiera de estos símbolos (<, >, >, <) es una Desigualdad. Ejemplo: 5 x 2 -4 x+7 < 2 x+3 4 x-3 > 7 x+5 Al resolver una desigualdad se encuentra un conjunto con aquellos números reales que la hacen verdadera. Al conjunto solución se le llama intervalo.

Tipos de intervalos Nombre Notación de conjuntos Abierto {x: a < x < b} Cerrado {x: a < x < b} Semiabierto: Por la izquierda {x: a < x < b} Por la derecha {x: a < x < b} Infinito: {x: x < b} {x: x > a} Gráfica Notación de intervalos a a x x b b (a, b) [a, b] a a x x b b (a, b] [a, b) b b a a x x (- , b] (- , b) [a, ) (a, )

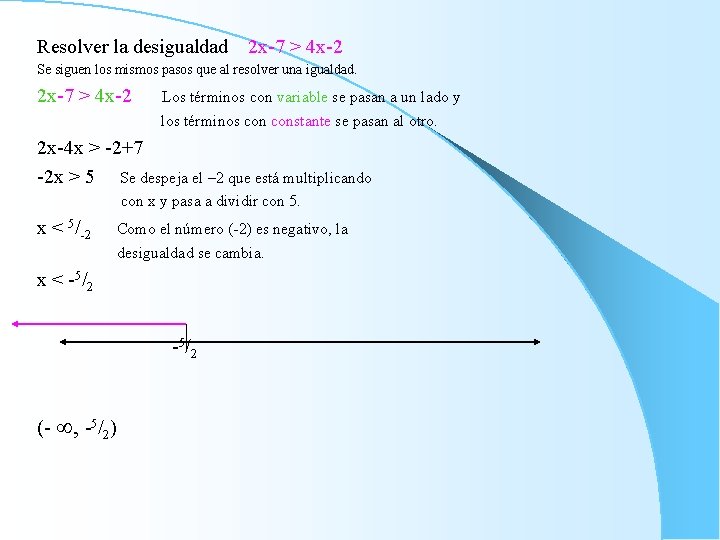
Resolver la desigualdad 2 x-7 > 4 x-2 Se siguen los mismos pasos que al resolver una igualdad. 2 x-7 > 4 x-2 Los términos con variable se pasan a un lado y los términos constante se pasan al otro. 2 x-4 x > -2+7 -2 x > 5 Se despeja el – 2 que está multiplicando con x y pasa a dividir con 5. x < 5/-2 Como el número (-2) es negativo, la desigualdad se cambia. x < -5 / 2 (- , -5/2)

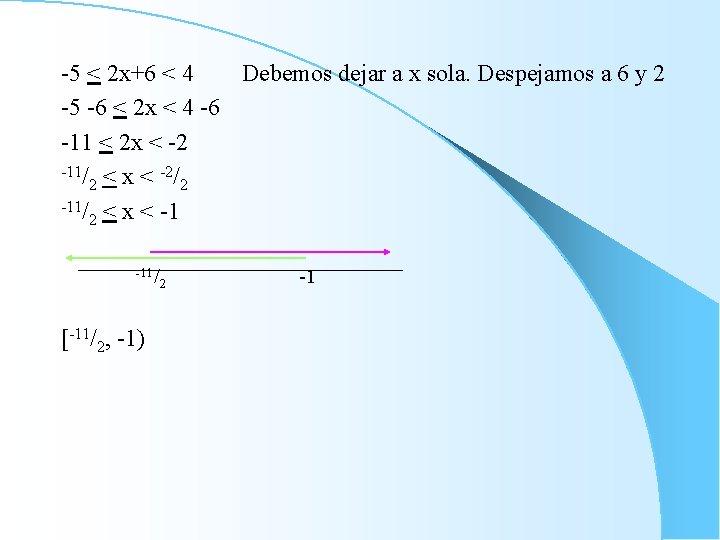
-5 < 2 x+6 < 4 Debemos dejar a x sola. Despejamos a 6 y 2 -5 -6 < 2 x < 4 -6 -11 < 2 x < -2 -11/ < x < -2/ 2 2 -11/ < x < -1 2 -11/ [-11/2, -1) 2 -1

x 2 -x < 6 Se pasa todo a un lado. x 2 -1 x -6 < 0 Se factoriza. (-3)(2)=-6, (-3)+(2)=-1 (x-3)(x+2) < 0 < indica que el resultado es negativo. (x-3) < 0 (x-3) > 0 x < +3 x > +3 (x+2) > 0 (x+2) < 0 x > -2 x < -2 -2 3 (-2, 3) -2 3 No tiene solución, no se cruzan

Tarea: Exprese el Conjunto solución 4 x-7 < 3 x+5 2. 7 x-1 < 10 x+4 3. 2 x+16 < x+25 4. 6 x-10 > 5 x-16 5. 10 x+1 > 8 x+5 6. 3 x+5 > 7 x+17 7. -6<2 x+3<-1 8. -3<4 x-9<11 9. -2<1 -5 x<3 10. 4<5 -3 x<7 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2+3 x<5 x+1<16 2 x-4<6 -7 x <3 x+6 (x+5)/(2 x-1) (2 x-3)/(x+1) 1/ < 5 x 7/ < 3 2 x 1/ (3 x-2)<4 3/ x+5 > 2 (x+2)(2 x 1)(3 x+7)>0 (2 x+3)(3 x-1)(x 2)<0

Valor absoluto Es la distancia que existe del origen (cero) a cualquier otro punto, ya sea hacia la izquierda o derecha. No existen distancias negativas; se designa mediante |x| y se define como: Ejemplo: |5| = 5 |-5| = +5 |-25 x|=25 x |-a|=a |b|=b |-4 x 2|= 4 x 2 Propiedades del valor absoluto I. |ab|=|a|*|b| |(2)(-3)|=|2|*|-3|=2*3=6 II. |a/b|=|a|/|b| |-4/2|=|-4|/|2|= 4/2 =2 III. |a+b|< |a|+|b| |-3+2|< |-3|+|2| IV. |a-b| > ||a| - |b|| |2 -3|> ||2|-|3||

Resuelva la desigualdad. |3 x-5| > 1 lo que está dentro del valor absoluto, puede ser positivo +(3 x-5) > 1 3 x > 1+5 3 x > 6/3 x>2 o negativo -(3 x-5) > 1 3 x-5 < 1/-1 3 x < -1+5 x < 4/3

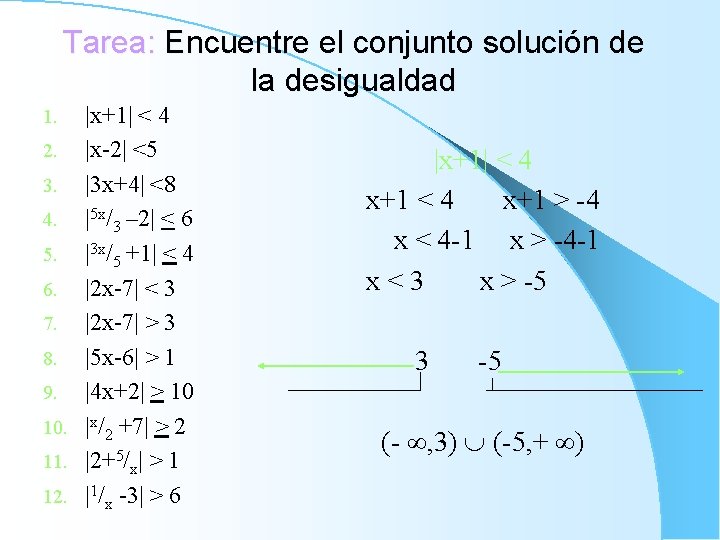
Tarea: Encuentre el conjunto solución de la desigualdad |x+1| < 4 2. |x-2| <5 3. |3 x+4| <8 4. |5 x/3 – 2| < 6 5. |3 x/5 +1| < 4 6. |2 x-7| < 3 7. |2 x-7| > 3 8. |5 x-6| > 1 9. |4 x+2| > 10 10. |x/2 +7| > 2 11. |2+5/x| > 1 12. |1/x -3| > 6 1. |x+1| < 4 x+1 > -4 x < 4 -1 x > -4 -1 x<3 x > -5 3 -5 (- , 3) (-5, + )

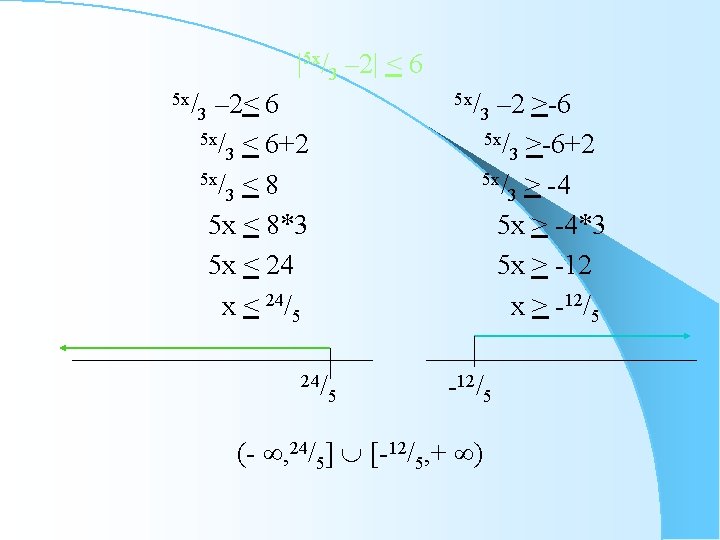
|5 x/3 – 2| < 6 5 x/ 3 – 2< 5 x/ < 3 6 6+2 8 5 x < 8*3 5 x < 24/5 24/ 5 x/ 3 – 2 >-6 5 x/ >-6+2 3 5 x/ > -4 3 5 x > -4*3 5 x > -12/5 5 -12/5 (- , 24/5] [-12/5, + )

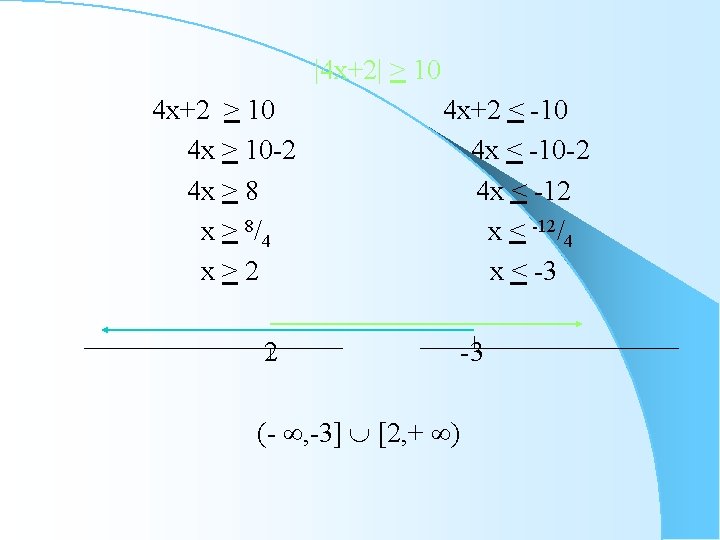
|4 x+2| > 10 4 x+2 > 10 4 x > 10 -2 4 x > 8/ 4 x>2 2 4 x+2 < -10 4 x < -10 -2 4 x < -12/4 x < -3 -3 (- , -3] [2, + )

Aunque el cálculo fue descubierto a fines del siglo XVII, sus fundamentos permanecieron en estado de confusión y desorden hasta que Cauchy y sus contemporáneos impusieron normas de rigor. Debemos a Cauchy la idea de basar el cálculo en una clara definición del concepto de límite. Tarea: Biografía de Cauchy

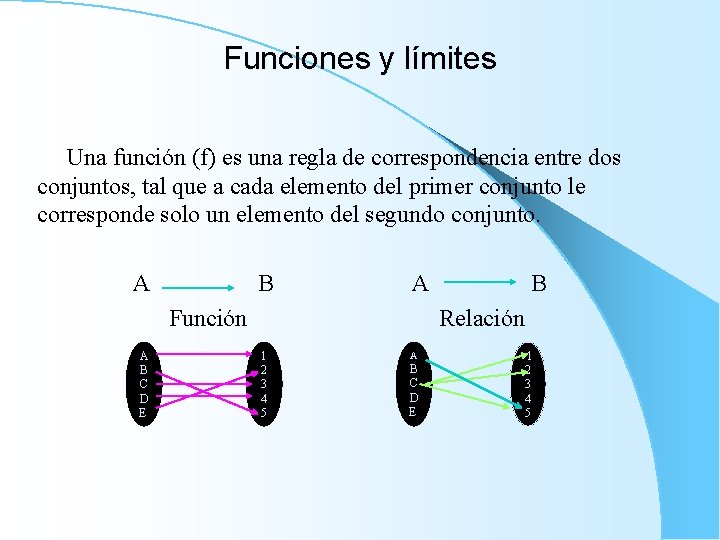
Funciones y límites Una función (f) es una regla de correspondencia entre dos conjuntos, tal que a cada elemento del primer conjunto le corresponde solo un elemento del segundo conjunto. A B A Función A B C D E B Relación 1 2 3 4 5 A B C D E 1 2 3 4 5

Conjunto: agrupación de cosas, elementos u objetos con características en común. Dominio: conjunto en el cual se encuentra la variable independiente Rango: Conjunto en el cual se encuentra la variable dependiente. Variable independiente: tiene valor por si misma Variable dependiente: para existir depende del valor de la variable independiente. Para denotar una función se usa una letra (f, g, F, etc). => F(x) se lee f de x ó f en x F(x) designa el valor que f le asigna a x.

x 3 - Si F(x) = 4 => F(2)= (2)3 - 4 = 8 -4 = 4 F(-1)= (-1)3 - 4 = -1 -4 =-5 F(a)= (a)3 - 4 = a 3 - 4 F(a+h)= (a+h)3 -4 = a 3+3 a 2 h+3 ah 2+h 3 -4 Si F(x) = x 2 - 2 x => F(4)= (4)2 - 2(4) = 16 -8 = 8 F(4+h)= (4+h)2 - 2(4+h) = 16+8 h+h 2 -(8+h) = 16+8 h+h 2 -8 -h = h 2+7 h+8 F(4+h)-F(4) = h 2+7 h+8 – 8 = h 2+7 h F(4+h)-F(4)/ (h 2+7 h)/ h = h(h+7)/ h = h+7

G(x) = 1/x G(a) = 1/a G(a+h) = 1/(a+h) G(a+h)-G(a) = 1/(a+h) - 1/a [G(a+h)-G(a)]/h = [1/(a+h) - 1/a]/h = [1(a)-(1)(a+h)/(a+h)(a)]/h = [a-a-h/(a+h)(a)]/h = [-h/(a+h)(a)] / h/1 = (-h)(1) / (a+h)(a)(h) = -h / (a 2+ah)h = -1 / (a 2+ah)

Para f(x) = x 2 -1, encuentre: a) b) c) d) e) f) g) h) i) f(1) = f(k) = f(-2) = f(-6) = f(0) = f(1/2) = f(2 t) = f(3 x) = f(1/x) = Para F(x) = 3 x 3+x, encuentre: a) b) c) d) e) f) g) h) F(-6) = F(1/2) = F(3. 2) = F( 3) = F(1/x ) = F(x) = F(2 x) = Para G(y) = 1/ y-1 encuentre: a) b) c) d) e) f) g) h) G(0) = G(2 y) = G(0. 999) = G(1. 01) = G(-x) = G(a) = G(2 t) = G(-y) =

Operaciones con funciones (f+g)(x) = f(x) + g(x) II. (f-g)(x) = f(x)-g(x) III. (f*g)(x) = f(x)*g(x) IV. (f / g)(x) = f(x) / g(x) V. (f g)(x) = f(g(x)) I. Ejemplo: Si f(x) = x 2 y g(x) = x+1 (f+g)(x) = f(x) + g(x) = x 2 + x+1 l (f-g)(x) = f(x)-g(x) = x 2 – (x+1) = x 2 – x - 1 III. (f*g)(x) = f(x)*g(x)= (x 2)(x+1) IV. = x 3 + x 2 IV. (f / g)(x) = f(x) / g(x) = (x 2)/(x+1) V. (f g)(x) = f(g(x))= f(x+1) = (x+1)2 l Clasificación parcial de funciones v. Función constante: f(x) = k; v. Función identidad: f(x) = x; v. Función lineal: f(x) = ax + b v. Función cuadrática: f(x) = ax 2 + bx + c v. Función cúbica: f(x)=ax 3+bx 2+cx+d v. Función polinomial: f(x)=axn+. . . +ax+a v. Función racional: f(x)= (axn+. . . +a)/(axn+. +a) v. Función valor absoluto: f(x)=| axn+. . +ax+a | v. Función exponencial: f(x) = ex v. Función logaritmica: f(x) = log x

Graficas de algunas funciones

Para f(x)= x/x-1 y g(x)= (1+x 2), encuentra cada valor si es posible: a) (f+g)(2)= b) (f*g)(0) c) (g/f)(3)= d) (f g)(0)= e) (g f)( 8)= f) (g f)(0)= 2 Para f(x)= x +x y g(x)=2/x+3, encuentra cada valor si es posible: a) (f-g)(2)= b) (f/g)(1) c) g 2(3)= d) (f g)(1)= e) (g f)(1)= f) (g g)(3)= Para f(x)= x 3+2 y g(x)=2/x-1, encuentra cada valor si es posible: (f/g)(x) b) (f g)(x)= c) (f+g)(x)= d) (g f)(x)= a) Si f(x)= (x 2 -1) y g(x)= 2/x, encuentra las fórmulas a) (f/g)(x) b) (f g)(x)= c) (f+g)(x)= d) (g f)(x)= e) (f-g)(x)= f) (f*g)(x)=

Introducción a los límites Estamos listos para una nueva idea importante, la noción de límite. Es ésta idea la que distingue el cálculo de otras ramas de las matemáticas. De hecho, podríamos definir el cálculo como un estudio de los límites. Noción intuitiva Considere la función determinada por la fórmula F(x)= (x 3 -1)/(x-1). Comencemos analizando la gráfica de la función; tabulemos: x -1 -½ 0 1 2 f(-1)= ((-1)3 -1)/((-1)-1)=(-1 -1)/(-1 -1)= -2/-2 = +1 y +1 0. 75 1 7 f(½) = ((-½)3 -1)/((-½)-1)=(-1/8 – 8/8)/(-½-2/2)= -9/8/- 3/2=+0. 75 f(1)= ((1)3 -1)/((1)-1)=(1 -1)/(1 -1)= 0/0 = Indeterminado Graficando lo tabulado: ¿Qué pasa de 0 a 2?

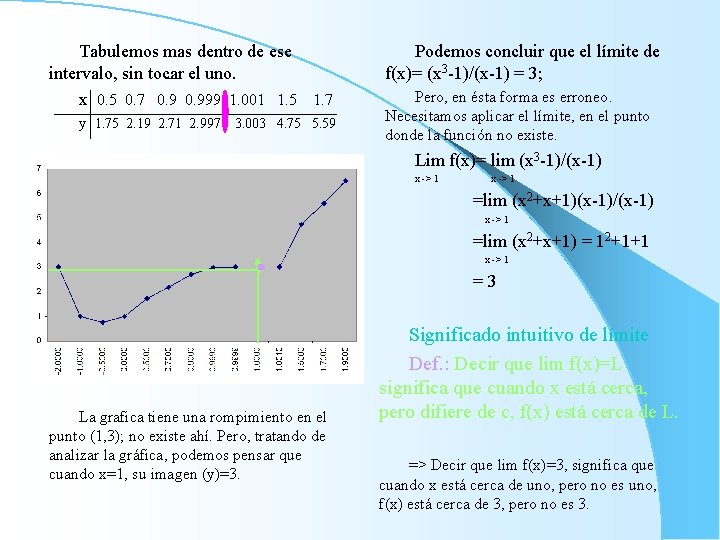
Tabulemos mas dentro de ese intervalo, sin tocar el uno. x 0. 5 0. 7 0. 999 1. 001 1. 5 1. 7 y 1. 75 2. 19 2. 71 2. 997 3. 003 4. 75 5. 59 Podemos concluir que el límite de f(x)= (x 3 -1)/(x-1) = 3; Pero, en ésta forma es erroneo. Necesitamos aplicar el límite, en el punto donde la función no existe. Lim f(x)= lim (x 3 -1)/(x-1) x -> 1 =lim (x 2+x+1)(x-1)/(x-1) x -> 1 =lim (x 2+x+1) = 12+1+1 x -> 1 =3 La grafica tiene una rompimiento en el punto (1, 3); no existe ahí. Pero, tratando de analizar la gráfica, podemos pensar que cuando x=1, su imagen (y)=3. Significado intuitivo de límite Def. : Decir que lim f(x)=L significa que cuando x está cerca, pero difiere de c, f(x) está cerca de L. => Decir que lim f(x)=3, significa que cuando x está cerca de uno, pero no es uno, f(x) está cerca de 3, pero no es 3.

Ejemplos: Encuentre: v. Lim(4 x-5)=4(3)-5 = 12 -5 = 7 x 3 v. Lim(x 2 -x-6)/(x-3)=[(32 -3 -6)]/(3 -3) x 3 =[(9 -9)]/(3 -3) =0/0= Como nos dió infinito el resultado, no se debe resolver así. Debemos factorizar el numerador. Propiedades de la raíz. (a*b) = a * b a/b = a / b (a+b) a + b a-b a - b a* a = (a*a) = a 2 = a v Lim (x-1)/( (x-1))= x 1 v. Lim(x 2 -x-6)/(x-3)=lim x 3 (x+2)(x-3)/(x-3) x 3 = lim (x+2) = 3+2 = 5 x 3 Cuando x se acerca a 3, f(x) se acerca a 5. v. Lim (x-1)/( (x-1))=(1 -1)/( (1 -1)) x 1 = 0/ 0 = 0/0 = Para resolver esta función, necesitamos conocer las propiedades de la raíz. Lim ( (x-1))/( (x 1))= x 1 Lim ( (x-1)) = (1 -1) = 0 =0 x 1