Universidad Nacional Autnoma de Mxico Facultad de Estudios

Universidad Nacional Autónoma de México Facultad de Estudios Superiores Zaragoza Carrera de Psicología Proyecto PAPIME UNAM PE-302915 El uso didáctico del lenguaje natural en la enseñanza del lenguaje formal en la estadística en la FES Zaragoza. Mediana

Presentación La enseñanza de la estadística, así como de cualesquiera rama de las matemáticas, requiere el uso y dominio de recursos semióticos formales propios del llamado lenguaje matemático (signos, operaciones, fórmulas, reglas de combinación de signos, etc. ), sin embargo, éste también se da a conocer mediante recursos semióticos no formales (el habla cotidiana, los gestos y los movimientos corporales, además, de dibujos, esquemas, imágenes, objetos, colores, gráficas, etc. ). Este material se enmarca en el objetivo del proyecto PAPIME 302915, financiado por la UNAM. Consiste en usar recursos semióticos no formales para enseñar el lenguaje formal de la estadística. El tema aquí tratado es un ejemplo de su aplicación, coordinado por los responsables del proyecto y ejecutado por un equipo de becarios. La estructura de este material se muestra en la siguiente diapositiva. Dr. Eduardo Alejandro Escotto Córdova, responsable de la investigación. Dr. José Gabriel Sánchez Ruiz, corresponsable de la investigación. Carrera de Psicología, Facultad de Estudios Superiores Zaragoza, UNAM. Cd. de México, 2018

SUMARIO Mediana en el lenguaje natural Mediana para datos no agrupados cuando el número de datos es impar Mediana para datos agrupados cuando el número de datos es impar Definiciones de mediana Mediana para datos no agrupados cuando el número de datos es par Mediana para datos agrupados cuando el número de datos es par Ejemplo 3 Referencias Instrucciones Ejemplo 1 Ejemplo 2 Créditos

Instrucciones Este es un recurso interactivo que podrás manipular de la siguiente manera: • Puedes dar clic en cada uno de los títulos para saltar secciones o regresar al “Sumario”. • Para avanzar las animaciones usa las teclas de navegación que se encuentran en la esquina inferior derecha de tu teclado. La tecla derecha es para avanzar y la izquierda para retroceder. Para avanzar la diapositiva usa los botones que aparecen en cada una de ellas • Debes esperar a que se desencadenen todas las animaciones para poder dar otro clic y seguir avanzando.

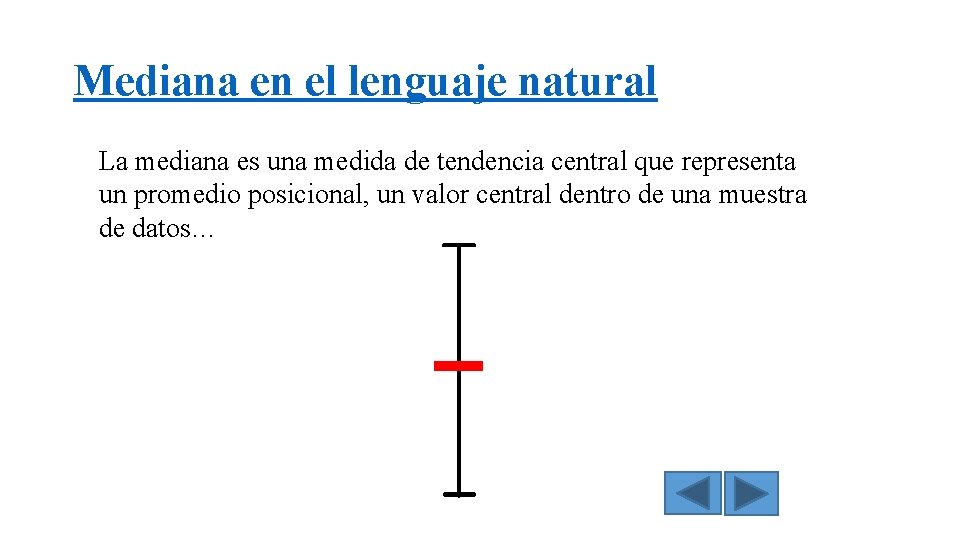
Mediana en el lenguaje natural La mediana es una medida de tendencia central que representa un promedio posicional, un valor central dentro de una muestra de datos…

Definiciones de mediana • Es el valor de la variable que no supera a no más de la mitad de las observaciones (Martínez, 2012). • Es el número que se encuentra en el centro o punto medio (valor central), una vez que los datos han sido ordenados de manera creciente (García, 2012). • El valor de la variable que deja por debajo la mitad del total de observaciones. La mediana deja la misma cantidad de casos por debajo y por encima de ella (Bologna, 2011).

Definiciones de mediana • Es el valor de la variable que no supera a no más de la mitad de las observaciones (Martínez, 2012). • Es el número que se encuentra en el centro o punto medio (valor central), una vez que los datos han sido ordenados de manera creciente (García, 2012). • El valor de la variable que deja por debajo la mitad del total de observaciones. La mediana deja la misma cantidad de casos por debajo y por encima de ella (Bologna, 2011).

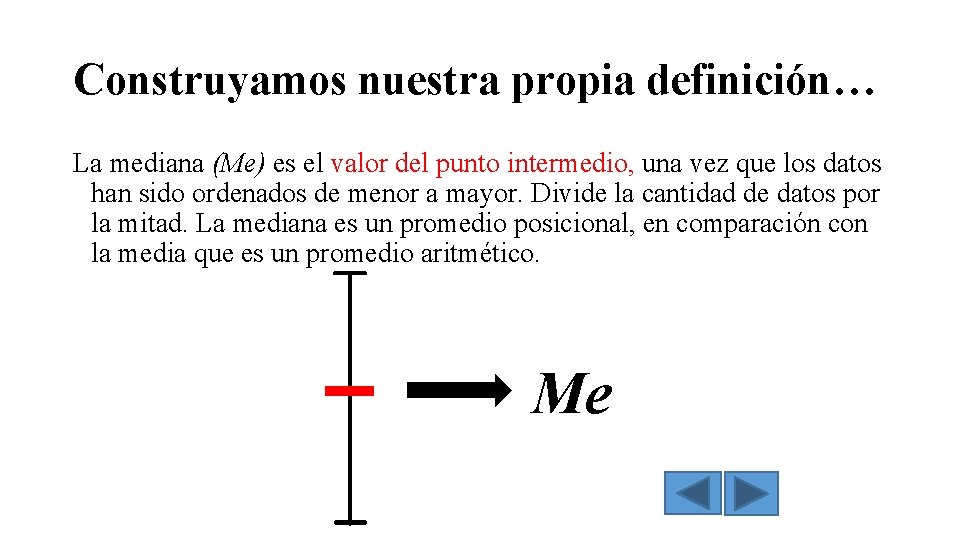
Construyamos nuestra propia definición… La mediana (Me) es el valor del punto intermedio, una vez que los datos han sido ordenados de menor a mayor. Divide la cantidad de datos por la mitad. La mediana es un promedio posicional, en comparación con la media que es un promedio aritmético. Me

Mediana para datos no agrupados cuando el número de datos es impar Donde: Lenguaje natural Expresión formal Me n Punto central, valor central Mediana Total, puntuaciones observadas, tamaño de la población o muestra Número de elementos de la muestra + Indica que al total de elementos se le suma uno (1) Adición El total de elementos más uno se divide entre dos Cociente __ 2

Mediana para datos no agrupados cuando el número de datos es par Donde: Lenguaje natural Expresión formal Me Punto central, valor central Mediana n 1 Primer valor central n Segundo valor central 2 + __ 2 Suma del primer valor central más el segundo valor central Adición La suma de los valores centrales se divide entre dos Cociente

Mediana para datos agrupados cuando el número de datos es impar La fórmula se lee de la siguiente manera…

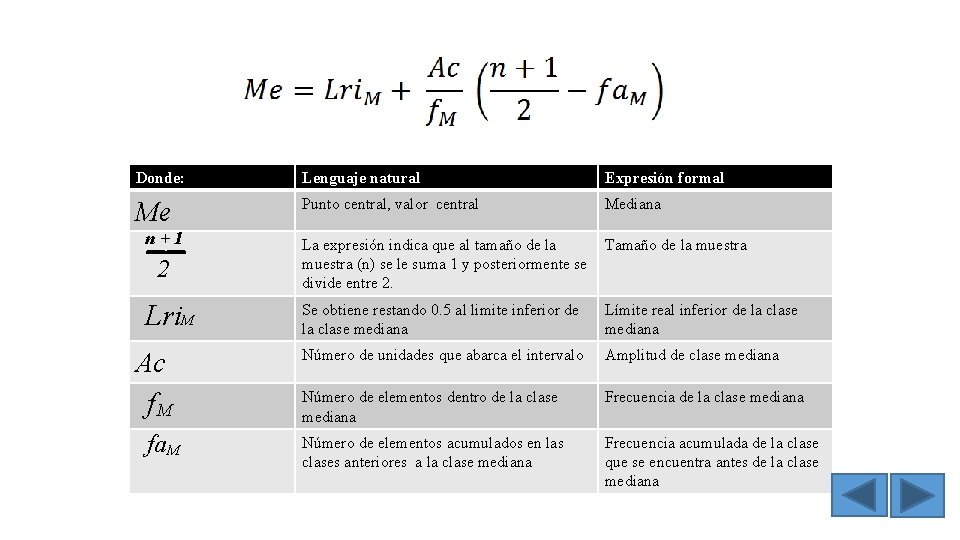
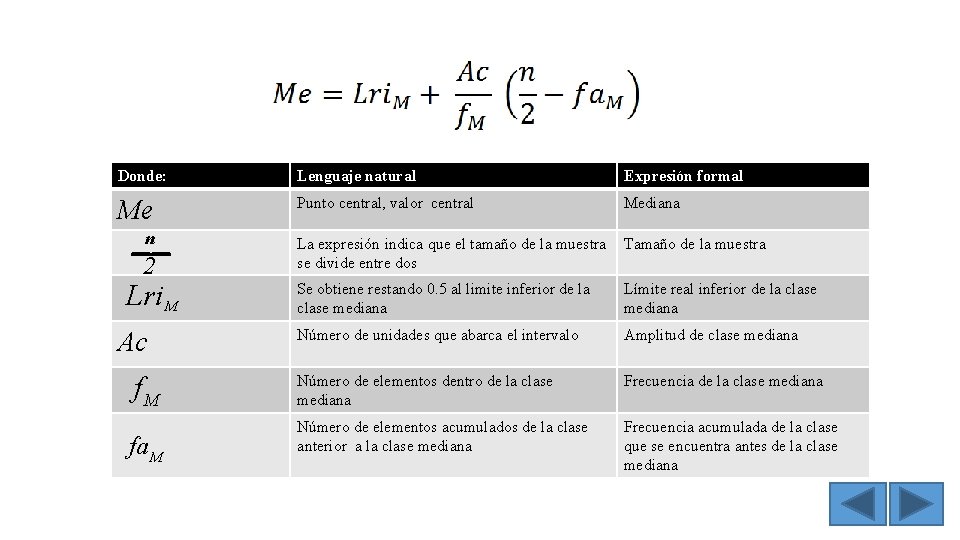
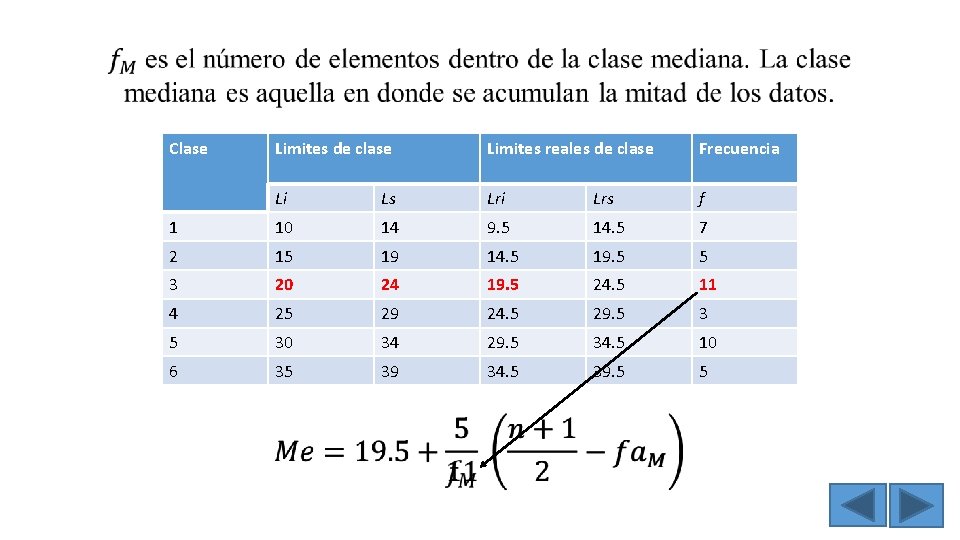
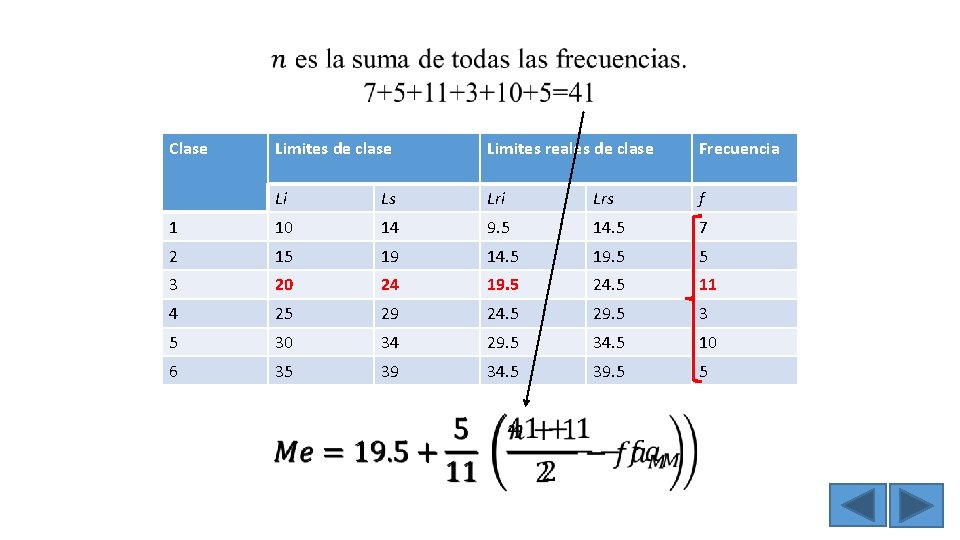
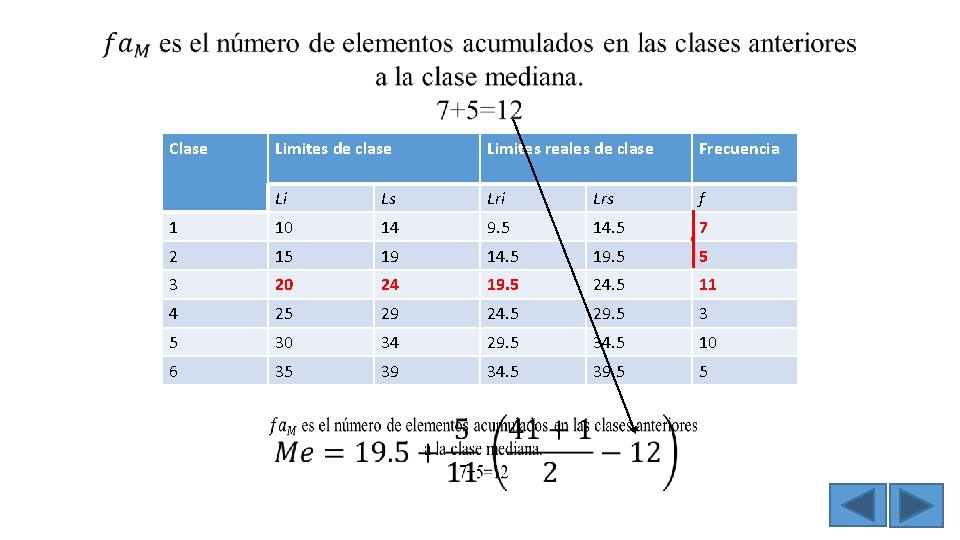
Donde: Lenguaje natural Expresión formal Me Punto central, valor central Mediana __ n+1 2 Lri. M La expresión indica que al tamaño de la Tamaño de la muestra (n) se le suma 1 y posteriormente se divide entre 2. Se obtiene restando 0. 5 al limite inferior de la clase mediana Límite real inferior de la clase mediana Número de unidades que abarca el intervalo Amplitud de clase mediana f. M Número de elementos dentro de la clase mediana Frecuencia de la clase mediana fa. M Número de elementos acumulados en las clases anteriores a la clase mediana Frecuencia acumulada de la clase que se encuentra antes de la clase mediana Ac

Mediana para datos agrupados cuando el número de datos es par Y se lee de la siguiente manera…

Donde: Lenguaje natural Expresión formal Me Punto central, valor central Mediana n __ 2 Lri M Ac f. M fa M La expresión indica que el tamaño de la muestra Tamaño de la muestra se divide entre dos Se obtiene restando 0. 5 al limite inferior de la clase mediana Límite real inferior de la clase mediana Número de unidades que abarca el intervalo Amplitud de clase mediana Número de elementos dentro de la clase mediana Frecuencia de la clase mediana Número de elementos acumulados de la clase anterior a la clase mediana Frecuencia acumulada de la clase que se encuentra antes de la clase mediana

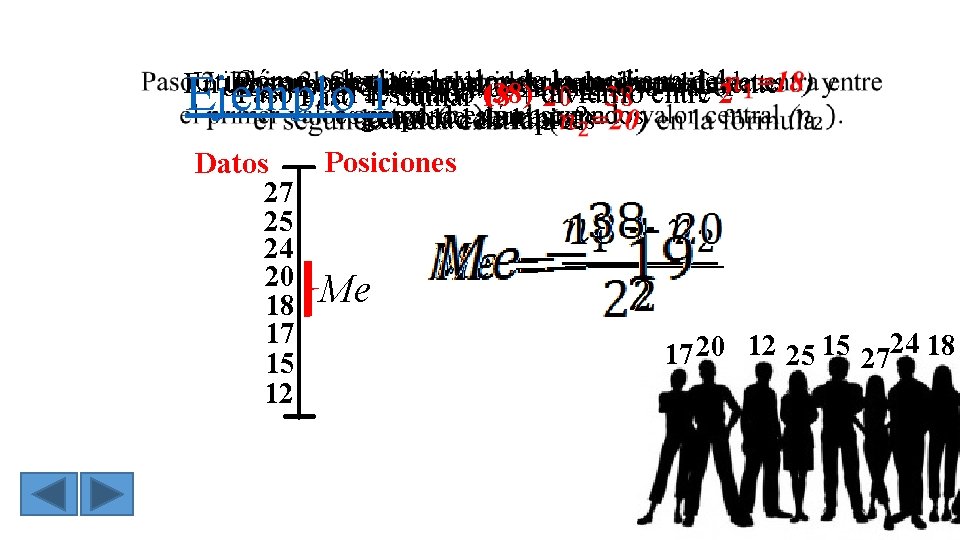
¿Cómo calcular el valor de la mediana del Utilizaremos esta fórmula ya que el número de datos En un grupo de alumnos, cada uno tiene diferente Paso 1: Ordenar los datos de menor a mayor Paso 5: El resultado (38) dividirlo entre 2 Paso 4: Sumar 18 + 20 = 38 es par y no están agrupados grupo de alumnos? cantidad de lápices Ejemplo 1 Posiciones Datos 27 25 24 20 18 Me 17 15 12 17 20 12 25 15 2724 18

Un terapeuta realiza un registro de los niveles de depresión en cada El resultado indica que en la posición 5 se encuentra el sesión con su paciente. Desea saber cual es la mediana en los niveles Paso 2: Contar el número de datos, el total de datos sustituye número 28, el cual es el valor de la mediana. Paso 4: Dividir 10 ÷ 2 = 5 Paso 3: Sumar 9 + 1 = 10 de depresión de su paciente a “n” Nivel de Paso 1: Ordenarlos del menor al mayor. Sesión Ejemplo 2 Datos 8, 16, 19, 23, 28, 29, 32, 36, 41 1 2 3 4 5 6 7 8 9 Posiciones Usaremos ésta fórmula ya que el número de datos es impar y no están agrupados depresión 1 41 2 32 3 29 4 36 5 28 6 19 7 23 8 16 9 8

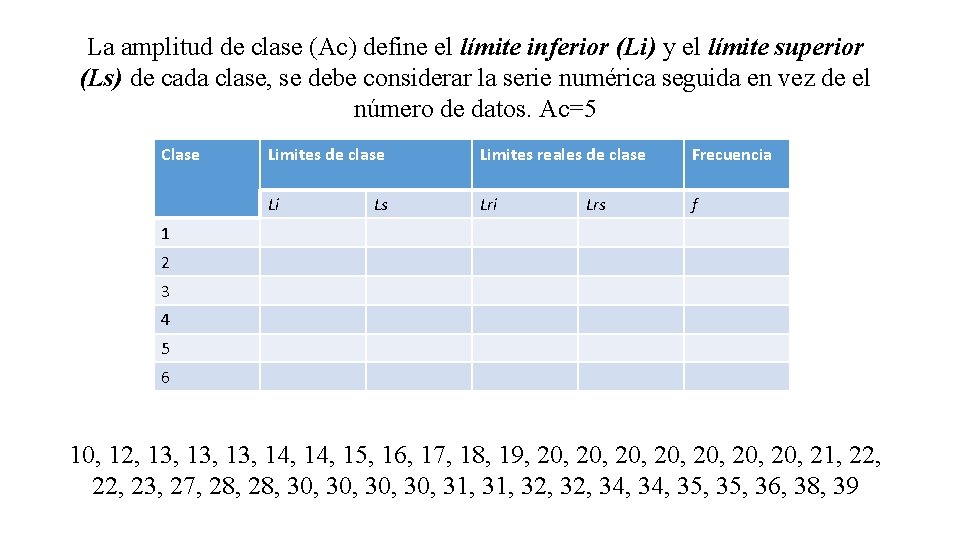
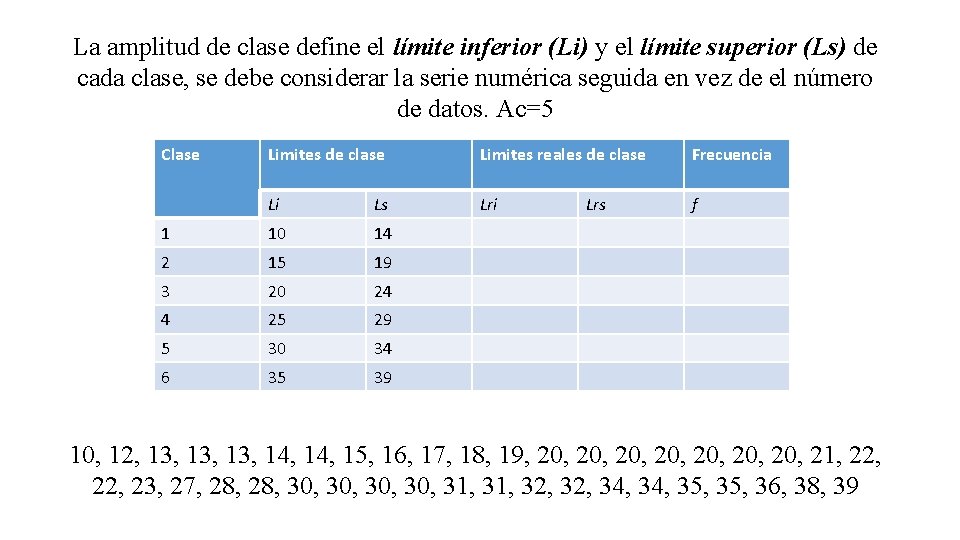
Ejemplo 3 Los siguientes datos son las respuestas motoras ante el dolor, medidas en milisegundos, de un grupo control conformado por 41 sujetos, ordenados de menor a mayor: 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39 Para agrupar estos datos necesitamos el rango (R), el número de clases (Nc), y la amplitud de clase (Ac) Rango: R= Xmax – Xmin R= 39 – 10= 29 R= 29

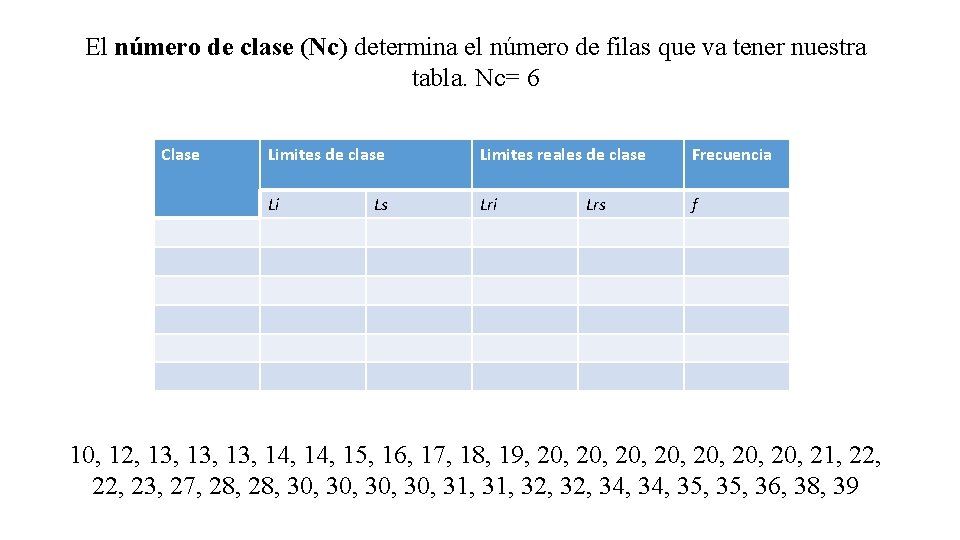
El número de clase (Nc) determina el número de filas que va tener nuestra tabla. Nc= 6 Clase Limites de clase Limites reales de clase Frecuencia Li Lri f Ls Lrs 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

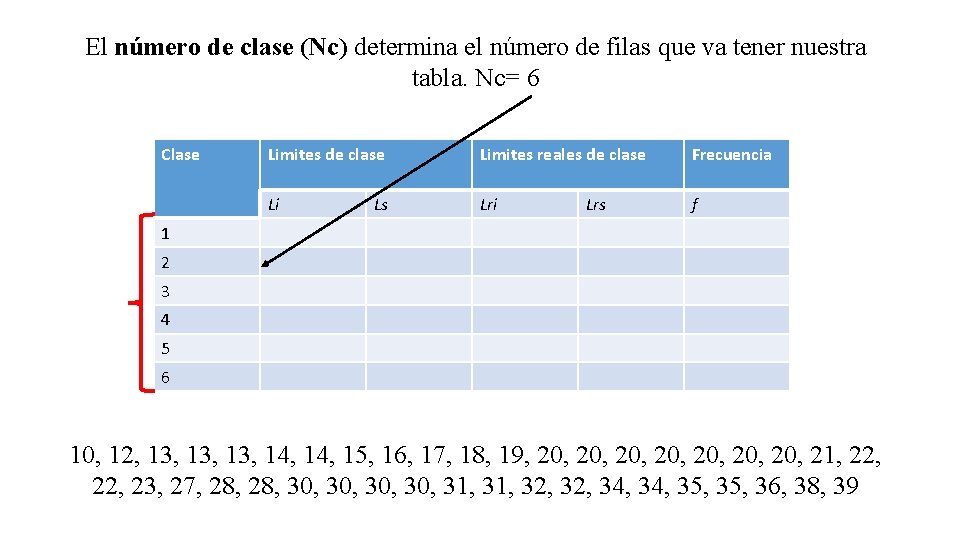
El número de clase (Nc) determina el número de filas que va tener nuestra tabla. Nc= 6 Clase Limites de clase Limites reales de clase Frecuencia Li Lri f Ls Lrs 1 2 3 4 5 6 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

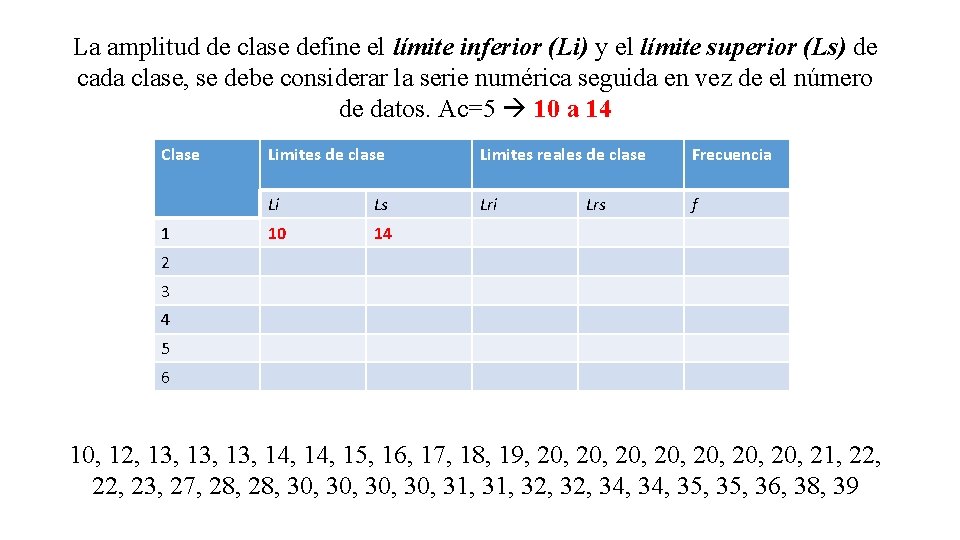
La amplitud de clase (Ac) define el límite inferior (Li) y el límite superior (Ls) de cada clase, se debe considerar la serie numérica seguida en vez de el número de datos. Ac=5 Clase Limites de clase Limites reales de clase Frecuencia Li Lri f Ls Lrs 1 2 3 4 5 6 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

La amplitud de clase define el límite inferior (Li) y el límite superior (Ls) de cada clase, se debe considerar la serie numérica seguida en vez de el número de datos. Ac=5 10 a 14 Clase 1 Limites de clase Limites reales de clase Frecuencia Li Ls Lri f 10 14 Lrs 2 3 4 5 6 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

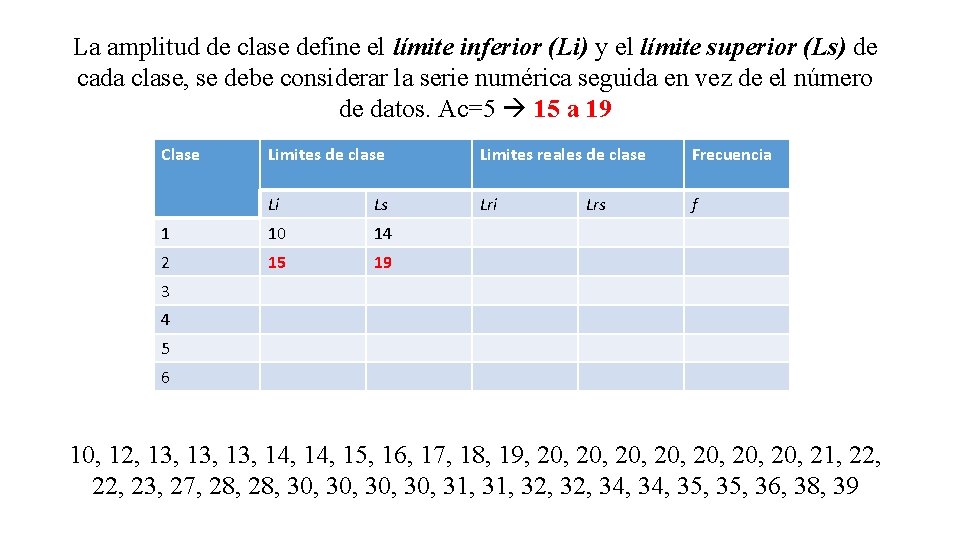
La amplitud de clase define el límite inferior (Li) y el límite superior (Ls) de cada clase, se debe considerar la serie numérica seguida en vez de el número de datos. Ac=5 15 a 19 Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri f 1 10 14 2 15 19 Lrs 3 4 5 6 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

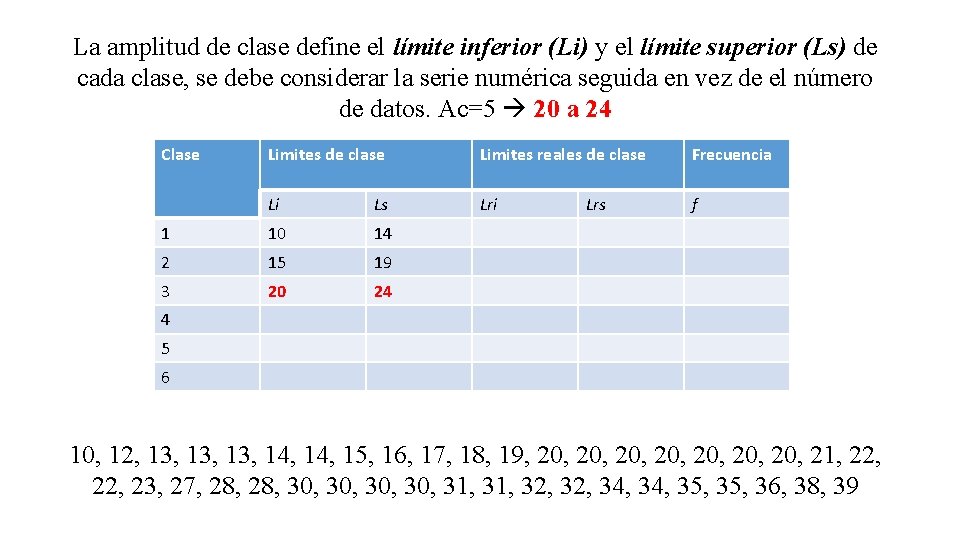
La amplitud de clase define el límite inferior (Li) y el límite superior (Ls) de cada clase, se debe considerar la serie numérica seguida en vez de el número de datos. Ac=5 20 a 24 Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri f 1 10 14 2 15 19 3 20 24 Lrs 4 5 6 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

La amplitud de clase define el límite inferior (Li) y el límite superior (Ls) de cada clase, se debe considerar la serie numérica seguida en vez de el número de datos. Ac=5 Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri f 1 10 14 2 15 19 3 20 24 4 25 29 5 30 34 6 35 39 Lrs 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

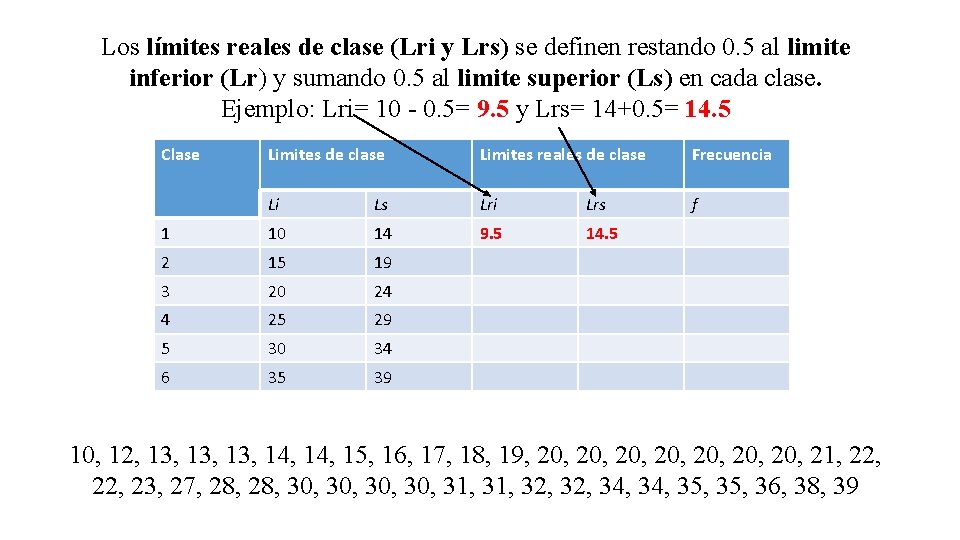
Los límites reales de clase (Lri y Lrs) se definen restando 0. 5 al limite inferior (Lr) y sumando 0. 5 al limite superior (Ls) Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri f 1 10 14 2 15 19 3 20 24 4 25 29 5 30 34 6 35 39 Lrs 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

Los límites reales de clase (Lri y Lrs) se definen restando 0. 5 al limite inferior (Lr) y sumando 0. 5 al limite superior (Ls) en cada clase. Ejemplo: Lri= 10 - 0. 5= 9. 5 y Lrs= 14+0. 5= 14. 5 Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 2 15 19 3 20 24 4 25 29 5 30 34 6 35 39 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

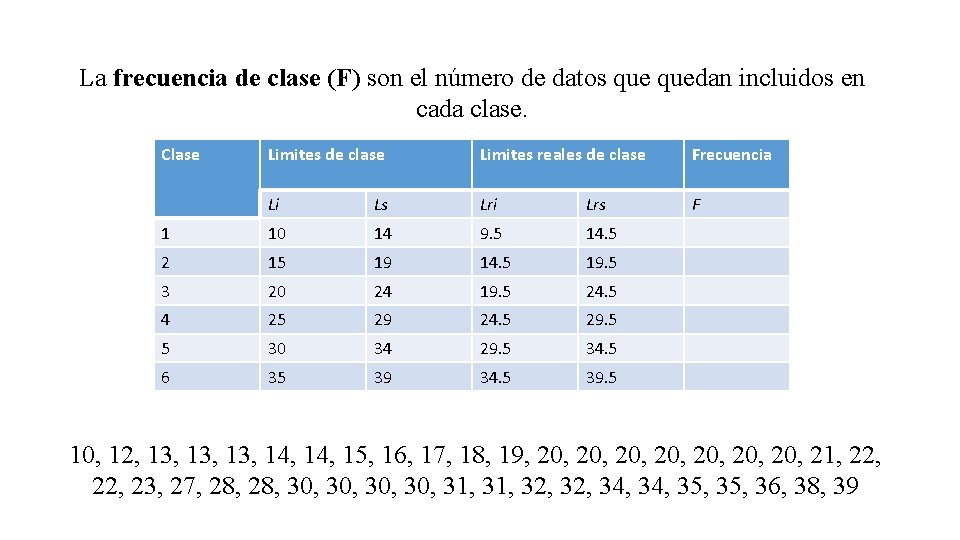
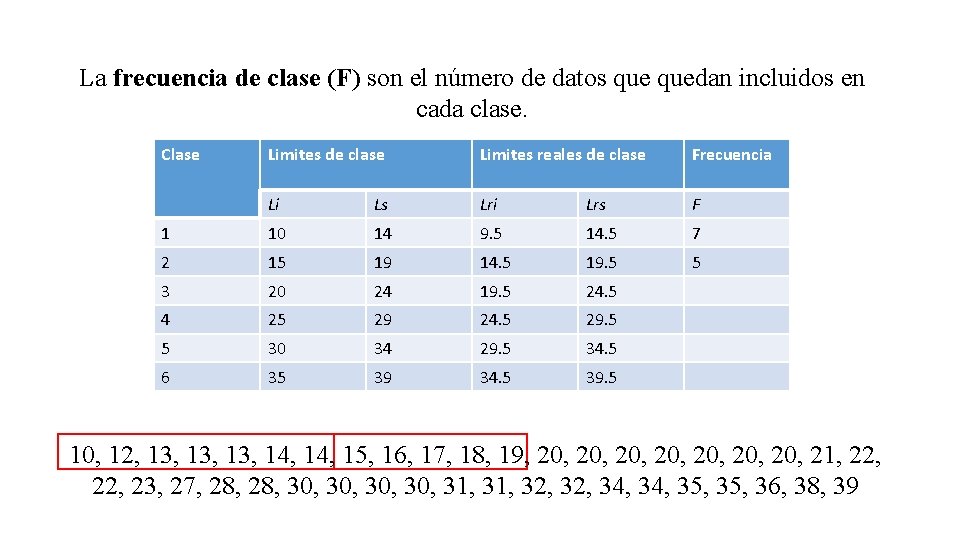
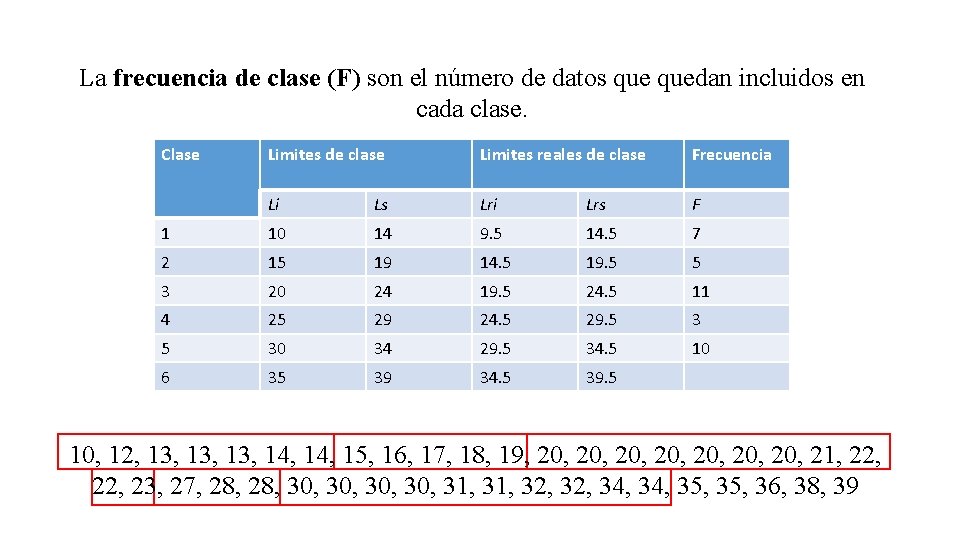
La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 2 15 19 14. 5 19. 5 3 20 24 19. 5 24. 5 4 25 29 24. 5 29. 5 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

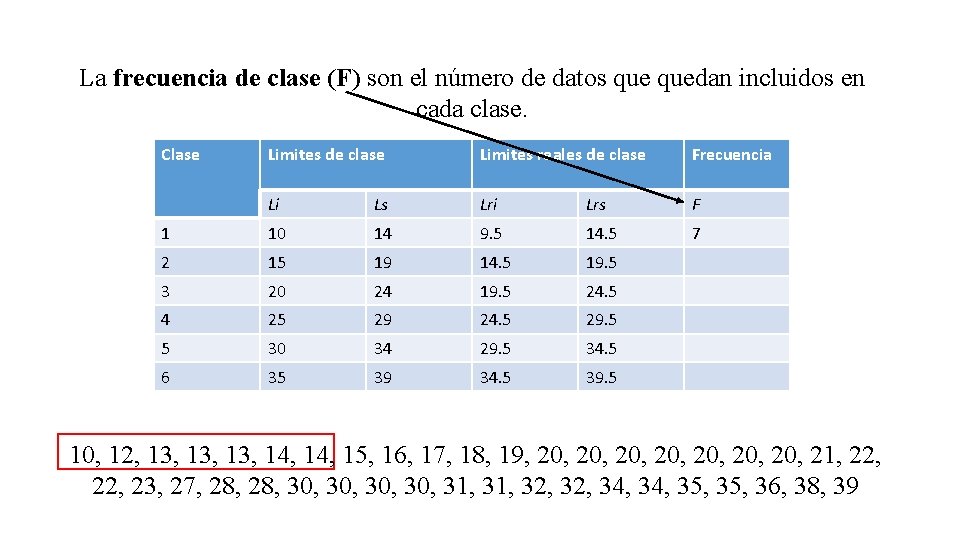
La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 3 20 24 19. 5 24. 5 4 25 29 24. 5 29. 5 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 4 25 29 24. 5 29. 5 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

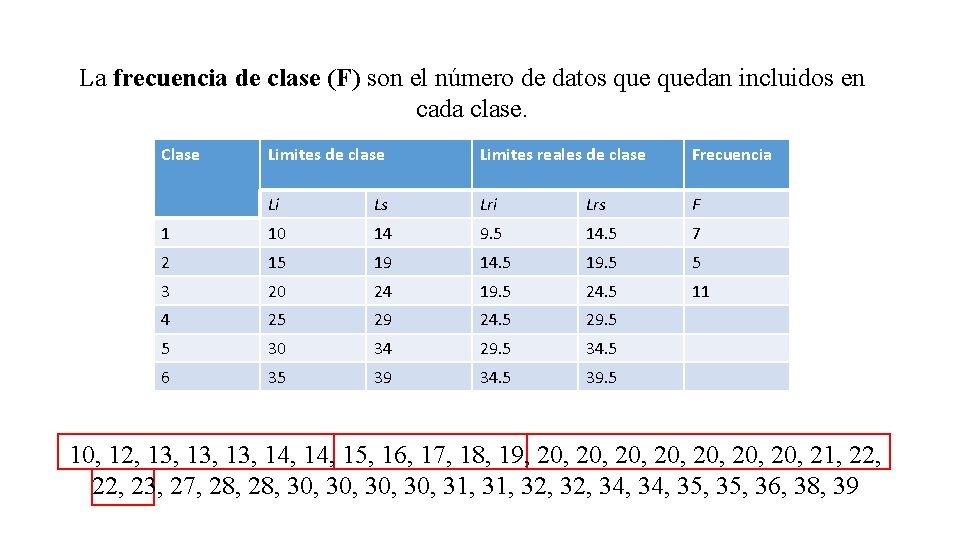
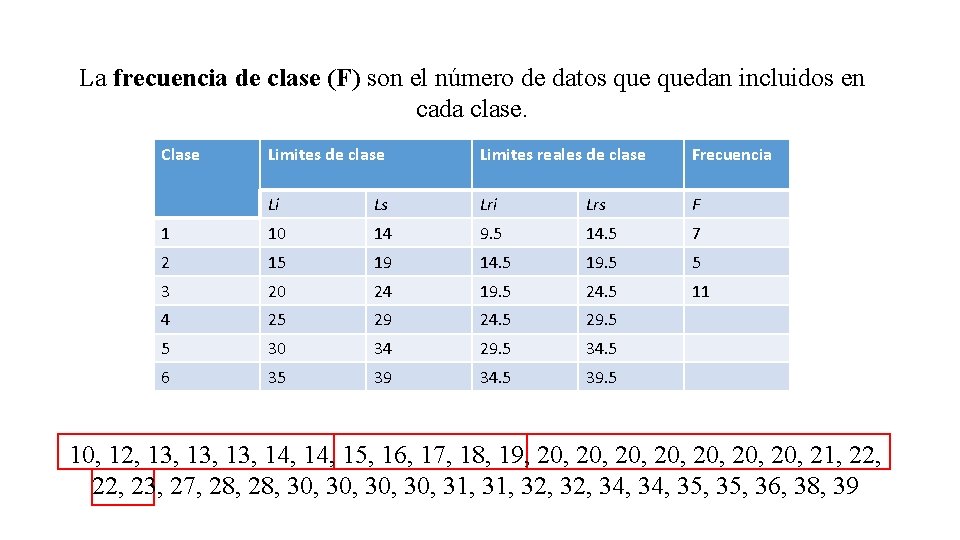
La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

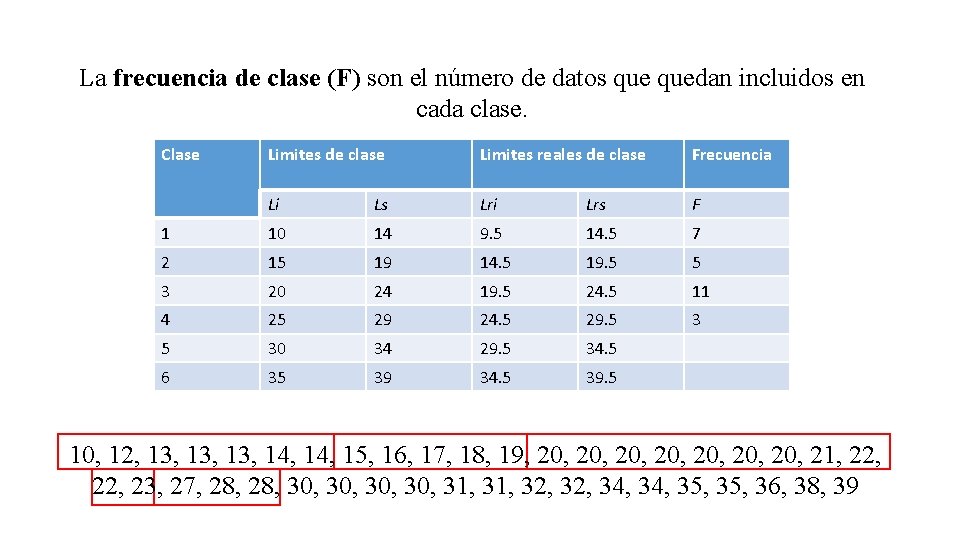
La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

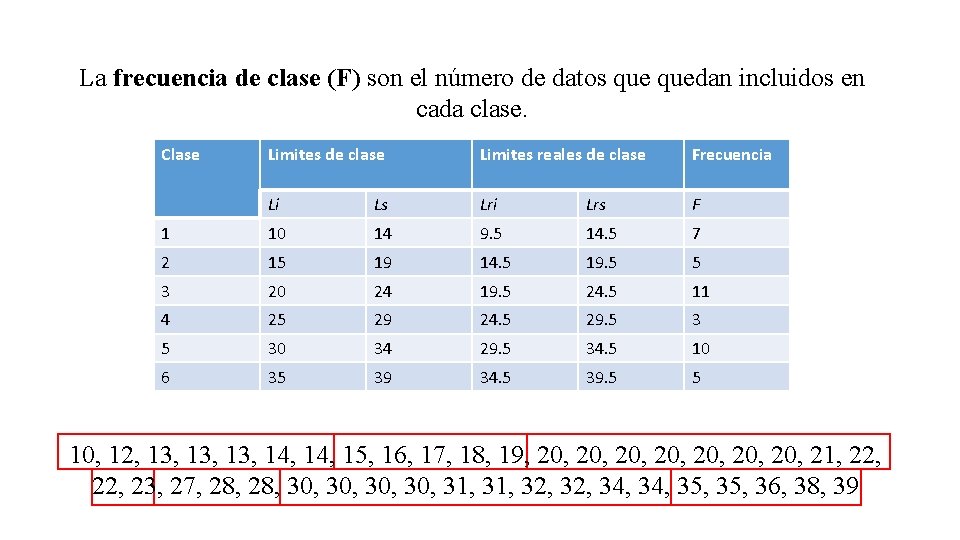
La frecuencia de clase (F) son el número de datos quedan incluidos en cada clase. Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs F 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5 10, 12, 13, 13, 14, 15, 16, 17, 18, 19, 20, 20, 21, 22, 23, 27, 28, 30, 30, 31, 32, 34, 35, 36, 38, 39

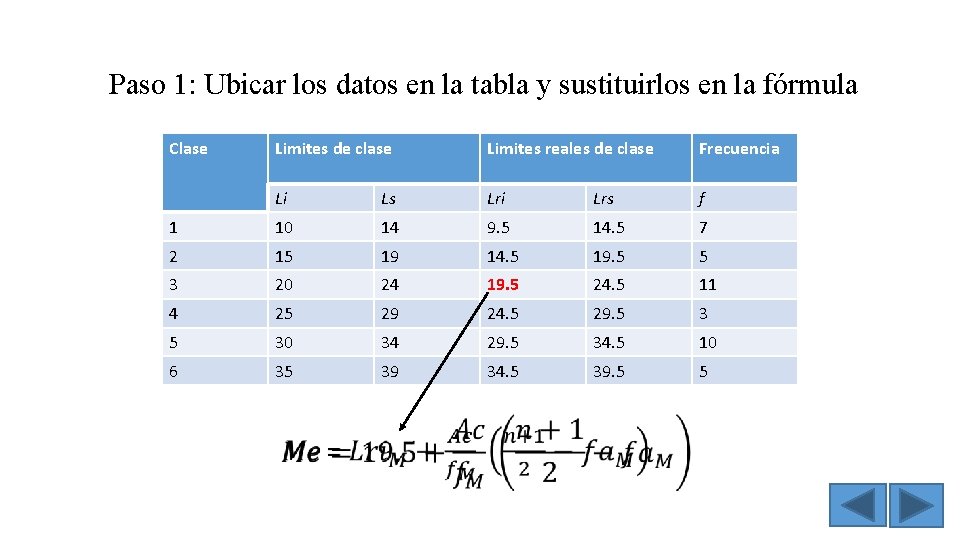
Una vez que tenemos nuestra tabla de datos agrupados podemos aplicar Paso 1: Ubicar los datos en la tabla y sustituirlos en la fórmula la siguiente fórmula Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

Paso 1: Ubicar los datos en la tabla y sustituirlos en la fórmula Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

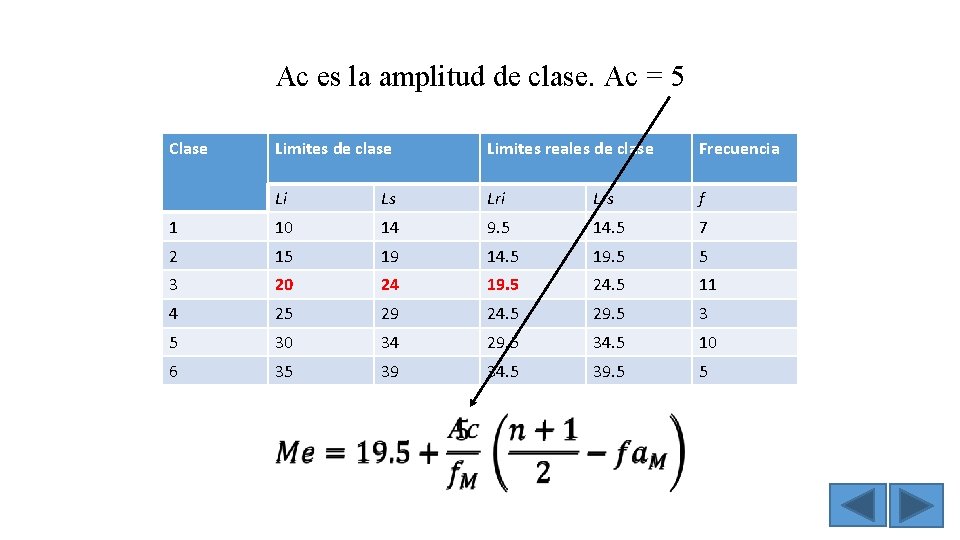
Ac es la amplitud de clase. Ac = 5 Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

Clase Limites de clase Limites reales de clase Frecuencia Li Ls Lri Lrs f 1 10 14 9. 5 14. 5 7 2 15 19 14. 5 19. 5 5 3 20 24 19. 5 24. 5 11 4 25 29 24. 5 29. 5 30 34 29. 5 34. 5 10 6 35 39 34. 5 39. 5 5

Paso 5: Multiplicar 0. 5 x 9 = 4. 5 Paso 6: Sumar 19. 5+4. 5= 24 Paso 3: Restar 21 -12=9

Referencias California State University Dominguez Hills (S/F). Diversity. Ilustración. Recuperado de http: //www 4. csudh. edu/chhsn/ssc/index. Bologna, E. (2011). Estadística para psicología y educación. Argentina: Brujas. García, U. L. (2012). Estadística y probabilidad. México: Uribe Competencias Matemáticas. Martínez, B. C. (2012). Estadística y muestreo. Colombia: Ecoe.

Agradecemos al Proyecto PAPIME UNAM PE-302915 EL USO DIDÁCTICO DEL LENGUAJE NATURAL EN LA ENSEÑANZA DEL LENGUAJE FORMAL EN LA ESTADÍSTICA EN LA CARRERA DE PSICOLOGÍA, financiado en su totalidad con recursos del mismo. Se agradece a la Universidad Nacional Autónoma de México, a través de la Dirección General de Asuntos del Personal Académico por su apoyo para este proyecto.

Directorio Carrera de Psicología Dr. Víctor Manuel Mendoza Núñez Director Mtra. Gabriela C. Valencia Chávez Jefa de la Carrera de Psicología Lic. Eduardo Arturo Contreras Ramírez Secretario Técnico Mtra. Julieta Becerra Castellanos Coordinadora de Etapa Básica, Psicología Mtra. Gloria M. Moreno Baena Coordinadora del Área de Psicología Educativa Mtra. Guillermina Netzahuatl Salto Coordinadora del Área de Psicología Clínica Mtra. Alejandra Luna García Coordinadora del Área de Psicología Social Dra. Fabiola Itzel Villa George Apoyo Área V Psicología del Trabajo y las Organizaciones Lic. Leonel Romero Uribe Responsable de Servicio Social Dr. Vicente J. Hernández Abad Secretario General Dra. Rosalinda Escalante Pliego Secretaria de Integración, Promoción y Desarrollo Académico M. en C. Faustino López Barrera Secretario de Planeación Lic. Sergio Silva Salgado Secretario Administrativo Dr. Edelmiro Santiago Osorio Jefe de la División de Posgrado e Investigación Dra. Mirna García Méndez Coordinadora de Trayectoria Escolar de las Ciencias de la Salud y del Comportamiento Dra. Martha Asunción Sánchez Rodríguez Coordinadora de Trayectoria Escolar de las Ciencias Químico Biológicas

Créditos: Becario Raúl Ruiz Rocha Propuesta Eduardo Alejandro Escotto Córdova Responsable del proyecto Revisión de recursos semióticos José Gabriel Sánchez Ruiz Corresponsable del proyecto Revisión de contenido estadístico Ana María Baltazar Ramos Colaboradora del proyecto Revisión de elementos pedagógicos Becario Raymundo Serrano Reyes Aplicación y edición de propuesta original Becario Mauricio Alfredo Ramírez Rodríguez Aplicación y edición de propuesta original

Marzo 2018