Funciones En nuestra vida cotidiana tenemos experiencia con

Funciones En nuestra vida cotidiana tenemos experiencia con relación o correspondencias de magnitudes. Ejemplos : • En un almacén , a cada producto le corresponde un precio. • Para una temperatura expresada en º C le corresponde un equivalente en º F. • A una profundidad determinada en un líquido le corresponde una presión hidrostática. • Un gas encerrado en un recipiente tiene una presión especifica. • El consumo de energía eléctrica se halla relacionado con el costo. • EL crecimiento poblacional se halla relacionado con el tiempo. • El cambio de rapidez en el movimiento de un móvil con respecto al tiempo. • El decaimiento de una sustancia radiactiva en función del tiempo. • El área de un circulo con el radio.

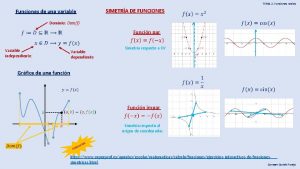
INTRODUCCION. Tipo especial de relaciones entre elementos de dos conjuntos A y B , llamadas funciones de A en B. Una función expresa la idea de una cantidad o magnitud que depende de otra u otras , o que está determinada por esta (s). Ejemplo. La longitud L de una circunferencia depende de su radio “r” Se lee: “ L es función de r. ” o “ L depende de r. ” Ejemplo. El volumen V de un cilindro recto depende de su radio (r) y su altura (h). Se lee: “ V es función de r y h” o “V depende de r y h”

Definición. Una función de A en B es una relación f С (A × B) que hace corresponder a cada elemento x del conjunto A a lo más con un elemento y del conjunto B , denotado por : y= f (x) ε B También se dice que f es una función definida en A y con valores en B , si a cada elemento x ε A le corresponde un único elemento y ε B A • Entrada Función : f ●B Salida Piense en una función como en una máquina, una máquina de calcular. Ésta toma un número (la entrada) y le produce un resultado ( la salida). A cada número en la entrada le corresponde un único número como salida, pero puede suceder que varios valores diferentes de entrada den el mismo valor de salida.

Al conjunto A se le llama conjunto de PARTIDA , y al conjunto B de LLEGADA. Notación: f : A x B y=f (x) Se lee “ f es una función de A en B. ” o “ f es una función definida en A y con valores en B. ” La notación y=f (x) se lee: “ y es el valor de la función f evaluada en x. ” o “ y es la imagen de x mediante f. ” Además : y=f (x) es equivalente a ( x , f ( x ) ) ε G r (f) : Gráfico de la función

Domino y Rango de una función Dominio. Es el conjunto de todos sus primeras componentes o antecedentes de los pares ordenados de f y se le denota por: Rango. Denominado también recorrido de la función f, al conjunto de las segundas componentes (imágenes o consecuentes) de todos los elementos A vía f ; y se le denota por:

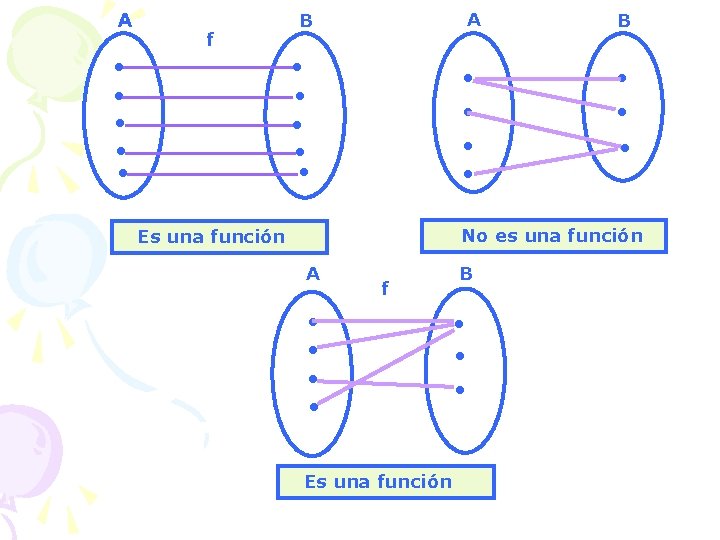
f A B ● ● ● ● ● No es una función Es una función A f B ● ● ● Es una función ●

REGLA O LEY DE CORRESPONDENCIA Es una expresión que permite calcular para cualquier su correspondiente imagen Por ejemplo : en el conjunto de llegada ( regla o ley de correspondencia ) al valor de x se le denomina variable independiente, y al valor se le llama variable dependiente. Más aún , una función está completamente determinada cuando se especifica su Dominio y Regla o Ley de correspondencia. Algunos ejemplos más de reglas o leyes de correspondencia.

Ejemplo 1. Sea Si . , entonces y Ejemplo 2. a) Halle el valor de K para que la relación : sea una función. b) Escribe el rango o recorrido.

Resolución. Como no pueden existir dos pares ordenados diferentes con la misma primera componente , para que R sea una función los pares ordenados deben ser iguales , de tal manera que : a) Remplazando , tenemos: b) Ejemplo 3. Dado el conjunto de pares ordenados : a) Halle los valores de a y b para que f sea una función. b) Determine el dominio y el recorrido de f.

Resolución. Por las consideraciones tomadas en el problema anterior: , entonces se forman las siguientes ecuaciones : Al resolver las ecuaciones se obtiene : a) Luego la función: b)

GRÁFICA DE UNA FUNCIÓN • Cuando los conjuntos de partida y de llegada A y B de una función f son conjuntos de números reales, esta función es llama una FUNCIÓN (de valor) REAL DE UNA VARIABLE REAL. • Una Función Real de una Variable Real es un conjunto de pares ordenados de números reales , y por lo tanto tiene una representación gráfica como conjunto de puntos en el plano (plano XY), . La variable (independiente) x se representa en el eje X (eje de abscisas) , mientras que la variable dependiente y=f (x) se representa en el eje Y (eje de ordenadas).

Aplicación de A B a) Una aplicación es un caso particular de una función. b) Una función f se llama aplicación de A en B si y sólo si Dom f =A. c) Un subconjunto f C ( A x B) es una aplicación de A en B si y sólo si Se lee para todo x perteneciente al conjunto A , existe un único elemento y perteneciente al conjunto B , tal que y=f (x) Notación. f es una aplicación de A en B se denota por: donde Dom f =A.

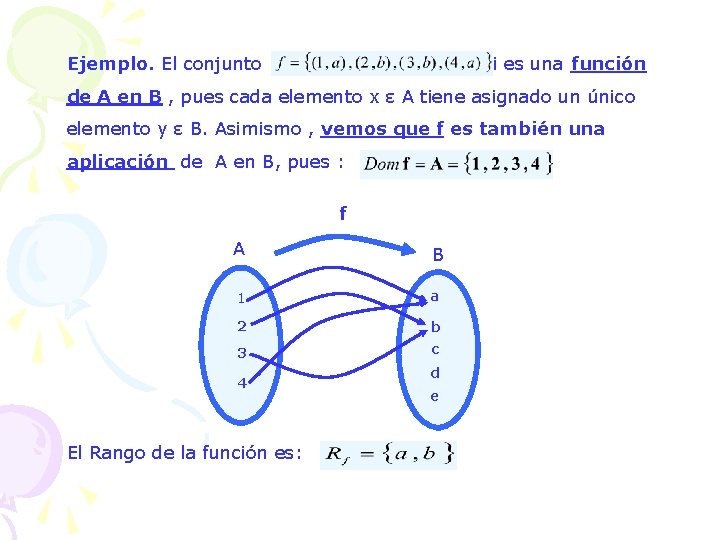
Ejemplo. El conjunto si es una función de A en B , pues cada elemento x ε A tiene asignado un único elemento y ε B. Asimismo , vemos que f es también una aplicación de A en B, pues : f A B 1 a 2 b 3 c 4 El Rango de la función es: d e

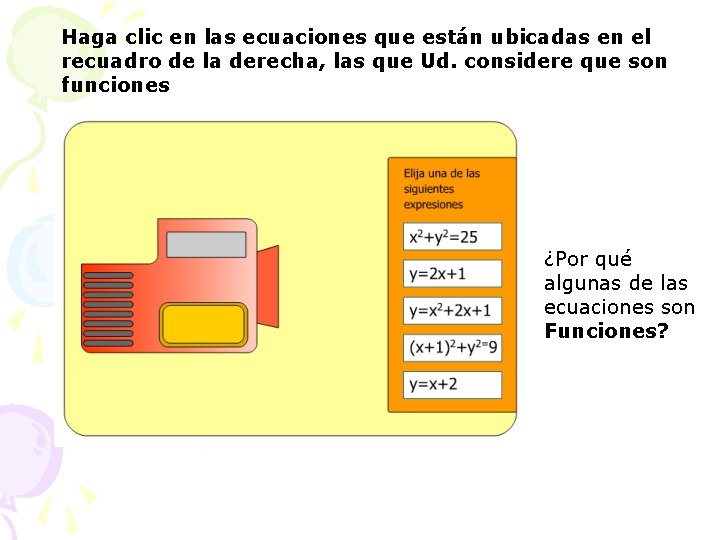
Haga clic en las ecuaciones que están ubicadas en el recuadro de la derecha, las que Ud. considere que son funciones ¿Por qué algunas de las ecuaciones son Funciones?

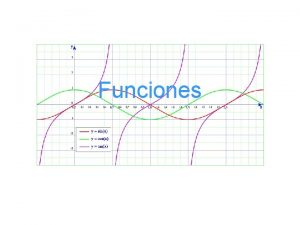
Reconocimiento de una función geométricamente.

FUNCIÓN LINEAL Ecuación de la Recta.

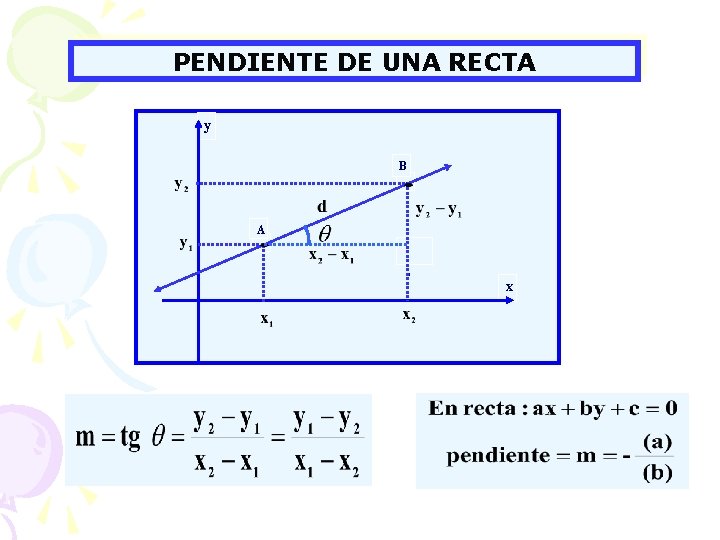
PENDIENTE DE UNA RECTA y B ● A ● . x

Distancia entre dos puntos de una Recta (d). Distancia de un Punto a una Recta. Ecuación general de la recta L : a x+ b y+c = 0 ● d L

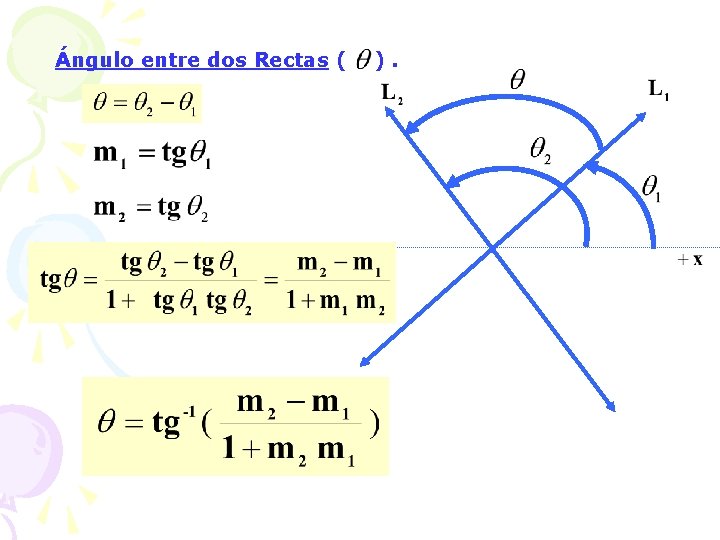
Ángulo entre dos Rectas ( ).

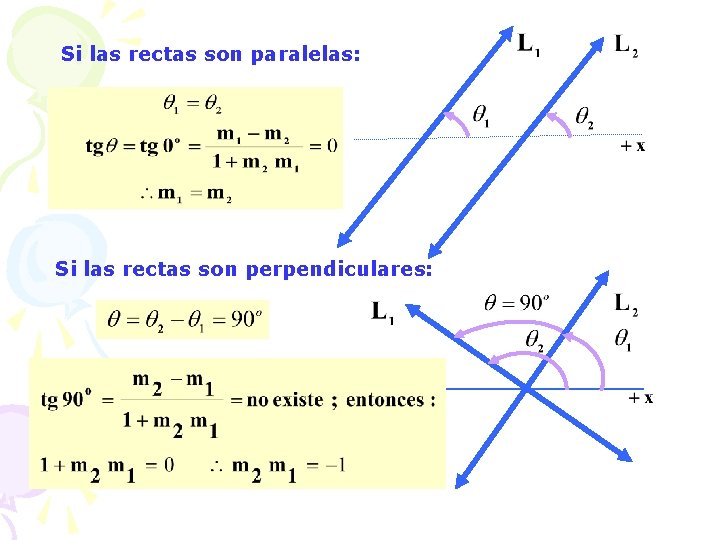
Si las rectas son paralelas: Si las rectas son perpendiculares:

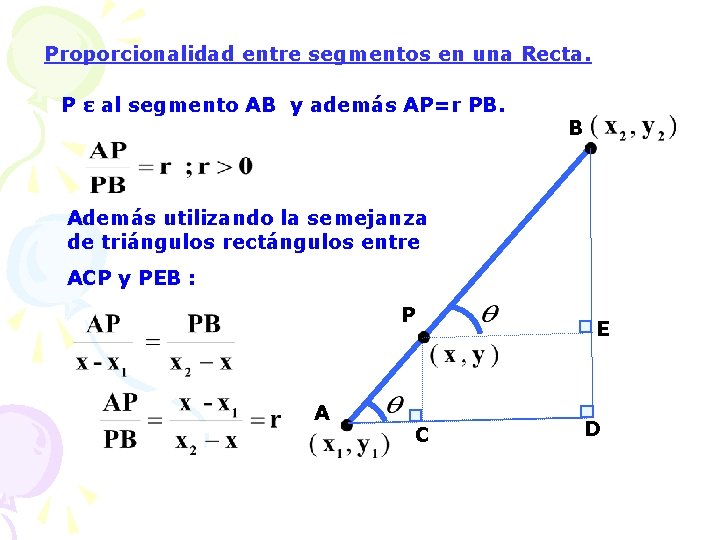
Proporcionalidad entre segmentos en una Recta. P ε al segmento AB y además AP=r PB. B Además utilizando la semejanza de triángulos rectángulos entre ACP y PEB : P A C E D

Despejando x : De la misma manera con y : Si r = 1 , encontramos que las coordenadas de P , corresponden a : ; Por lo tanto: P es punto medio.

PROBLEMAS 1. Determine el valor de la pendiente de la recta que contiene a los puntos dados. i) (2 , 3 ) y ( 4 , 8 ) Resolución. ii) ( 2 , -4 ) y ( 0 , -8 ).

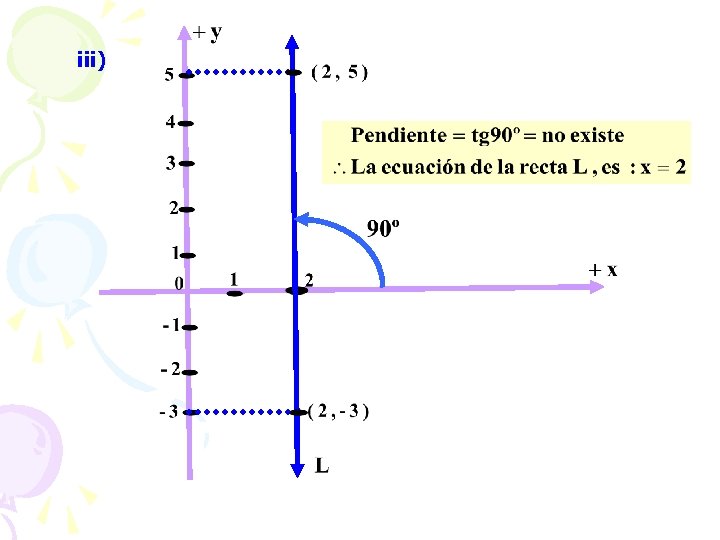
2. Halle la ecuación para cada recta. Escribe después su respuesta en la forma A x+B y+C=0. i) Pasa por (2, 3) con pendiente 4. ii) Con ordenada al origen 5 y pendiente 0. iii) Pasa por (2, -3) y (2, 5). Resolución.

ii) Se conoce la pendiente: m = 0 y b =5 , y la forma de la recta , entonces : , que es la ecuación de una recta horizontal. Se pide expresarla en la forma: . También se puede usar la forma punto pendiente: Considerando:

iii)

FUNCIÓN CUADRÁTICA Y = f (x) = a x 2 + b x + c ; a , b y c ε Reales y a≠ 0. Completando cuadrados : y = a ( x- h )2 + k , donde ( h , k ) corresponden a las coordenadas del vértice de la parábola. a>0 : y parábola Eje de Simetría = b 2 - 4 a c > 0 Corta al eje x en dos puntos (dos raíces reales y diferentes) La ecuación del eje de simetría (recta vertical) , corresponde a : . x x=h Las raíces son x 1 y x 2. El valor mínimo de la función: Ymin= k También : x 2 x 1 h =- (b)/(2 a) = ( x 1+x 2 )/2 ; k = f (h). V V : (h , k) V =Vértice

ii) = b 2 - 4 a c=0 , la parábola corta al eje x en un punto (dos raíces reales e iguales). y x X =h iii) =b 2 -4 a c < 0 , la parábola no corta al eje x. y No existen soluciones reales Existen dos raíces complejas y conjugadas x

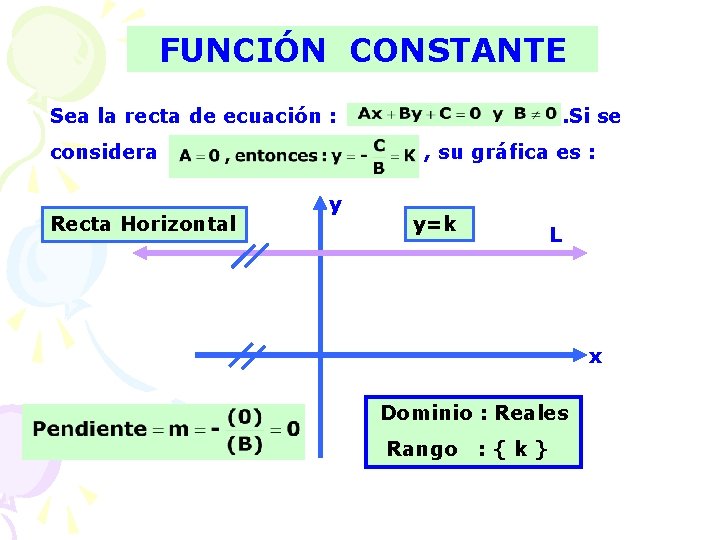
FUNCIÓN CONSTANTE Sea la recta de ecuación : considera Recta Horizontal . Si se , su gráfica es : y y=k L x Dominio : Reales Rango : {k}

Si en la ecuación se considera : su gráfica es: y x=k : Recta Vertical. No es una función. k 90º x L Dominio : { k } Rango : Reales

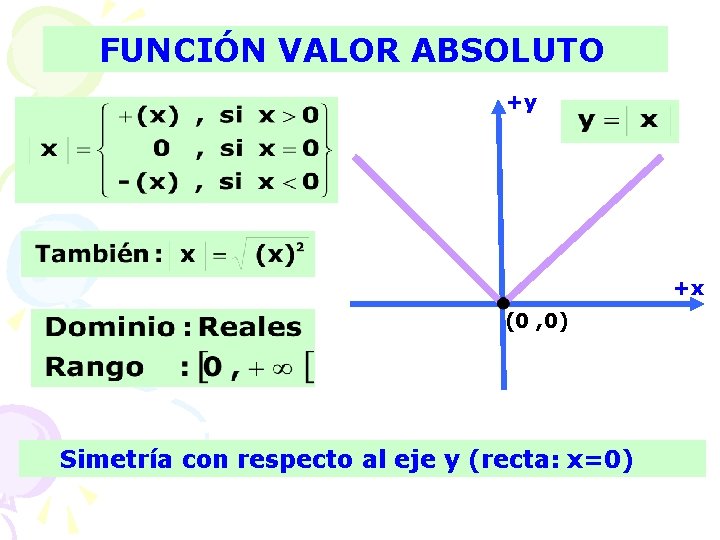
FUNCIÓN VALOR ABSOLUTO +y +x (0 , 0) Simetría con respecto al eje y (recta: x=0)

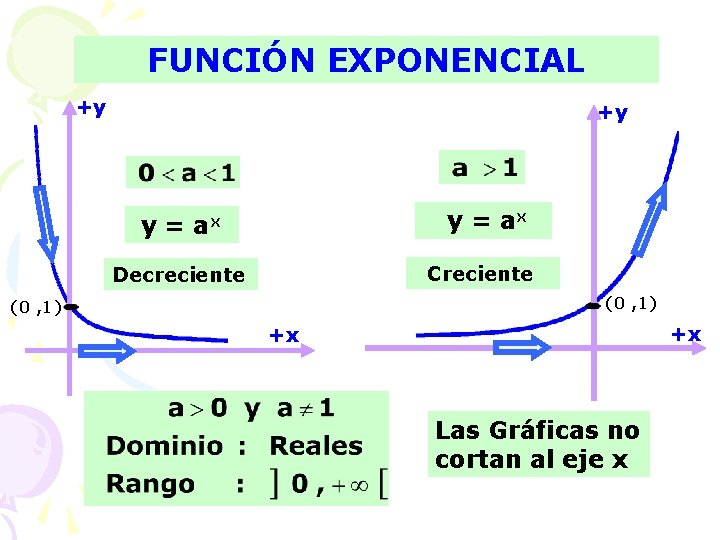
FUNCIÓN EXPONENCIAL +y +y y = ax Creciente Decreciente (0 , 1) +x +x Las Gráficas no cortan al eje x

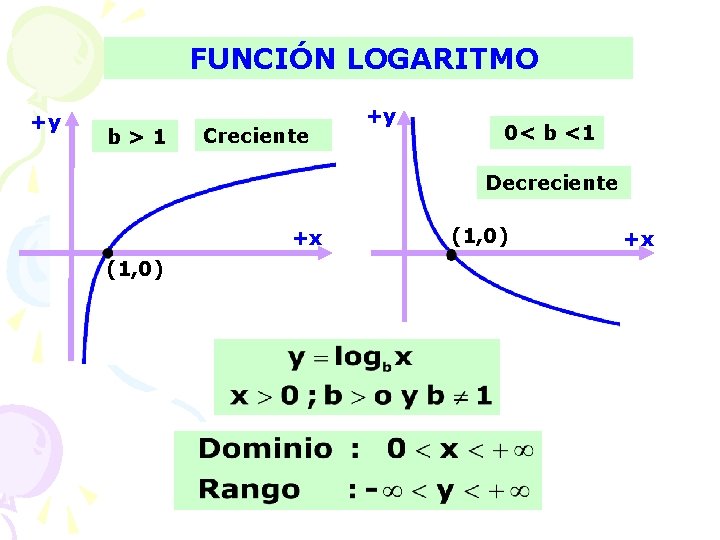
FUNCIÓN LOGARITMO +y b>1 Creciente +y 0< b <1 Decreciente +x (1, 0) +x

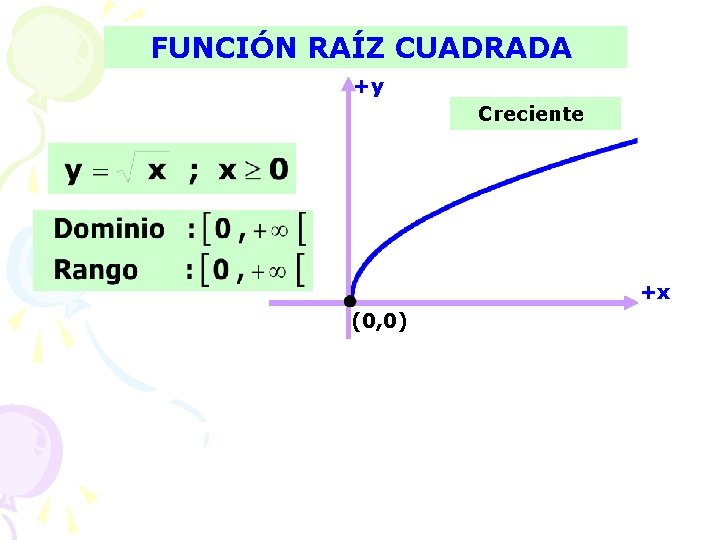
FUNCIÓN RAÍZ CUADRADA +y Creciente +x (0, 0)

FUNCIÓN RECÍPROCA +y Decreciente. (0, 0) +x Decreciente. El nombre de la gráfica es hipérbola equilátera. No corta al eje x e y. Simetría con respecto al origen : Función impar

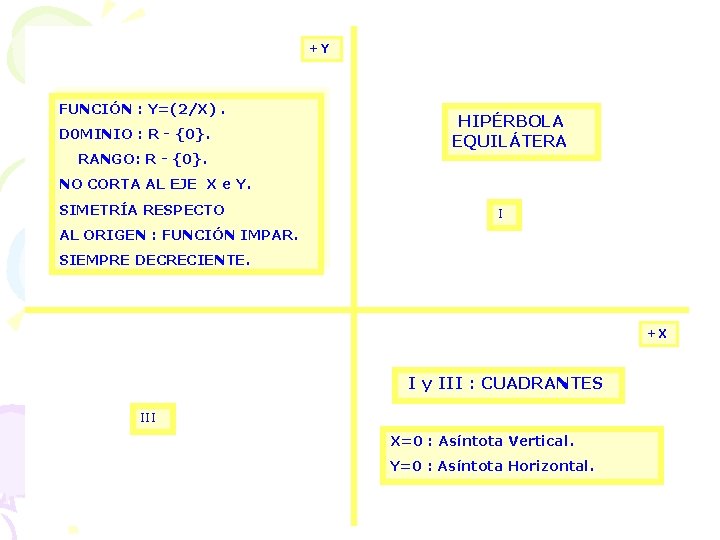
+Y FUNCIÓN : Y=(2/X). D 0 MINIO : R - {0}. HIPÉRBOLA EQUILÁTERA RANGO: R - {0}. NO CORTA AL EJE X e Y. SIMETRÍA RESPECTO I AL ORIGEN : FUNCIÓN IMPAR. SIEMPRE DECRECIENTE. +X I y III : CUADRANTES III X=0 : Asíntota Vertical. Y=0 : Asíntota Horizontal.

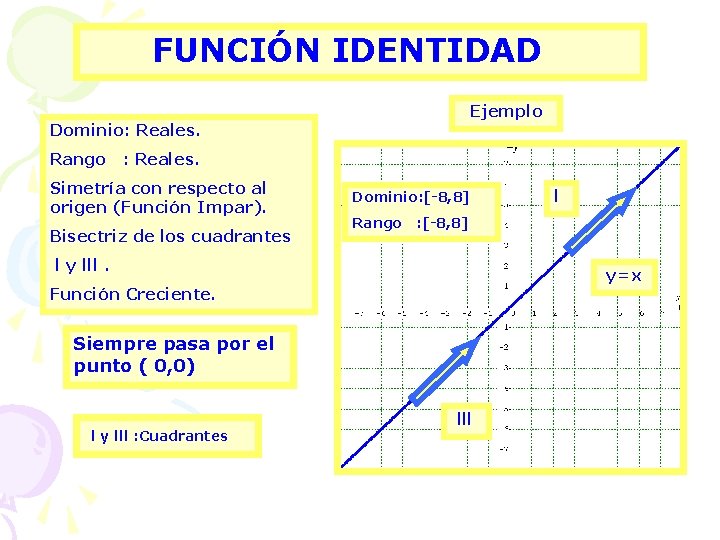
FUNCIÓN IDENTIDAD Ejemplo Dominio: Reales. Rango : Reales. Simetría con respecto al origen (Función Impar). Bisectriz de los cuadrantes Dominio: [-8, 8] Rango : [-8, 8] l y lll. y=x Función Creciente. Siempre pasa por el punto ( 0, 0) l y lll : Cuadrantes l lll

FUNCIÓN CÚBICA Ejemplo Dominio : Reales. Rango: Reales. Función Creciente. y=x 3 I Dominio: [-3, 3] Rango : [-27, 27] Simetría con respecto al origen (función impar). I y III: Cuadrantes Pasa por (0, 0). III

FUNCIONES RACIONALES Es una función de la forma : donde P y Q son funciones polinomiales y Q no es el polinomio cero. El dominio de una función racional está constituido por todos los números reales excepto aquellos donde el denominador Q es cero. Ejemplos :

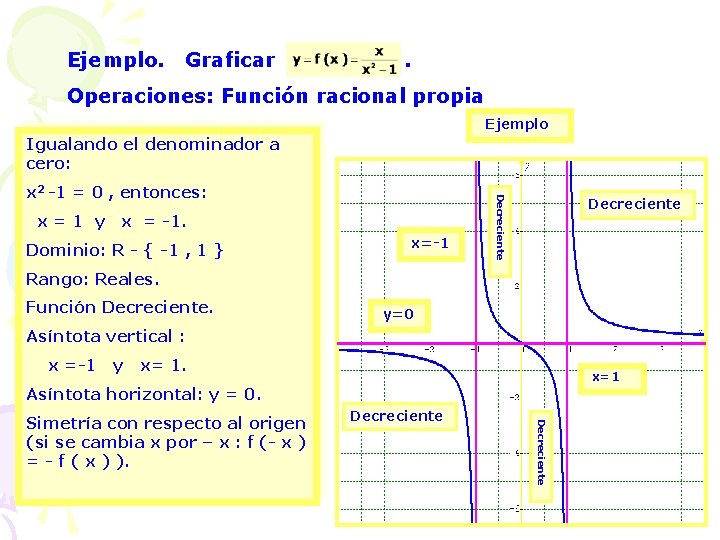
Ejemplo. Graficar . Operaciones: Función racional propia Ejemplo Igualando el denominador a cero: x=1 y x = -1. Dominio: R - { -1 , 1 } x=-1 Decreciente x 2 -1 = 0 , entonces: Decreciente Rango: Reales. Función Decreciente. y=0 Asíntota vertical : x =-1 y x= 1. x=1 Asíntota horizontal: y = 0. Decreciente Simetría con respecto al origen (si se cambia x por – x : f (- x ) = - f ( x ) ).

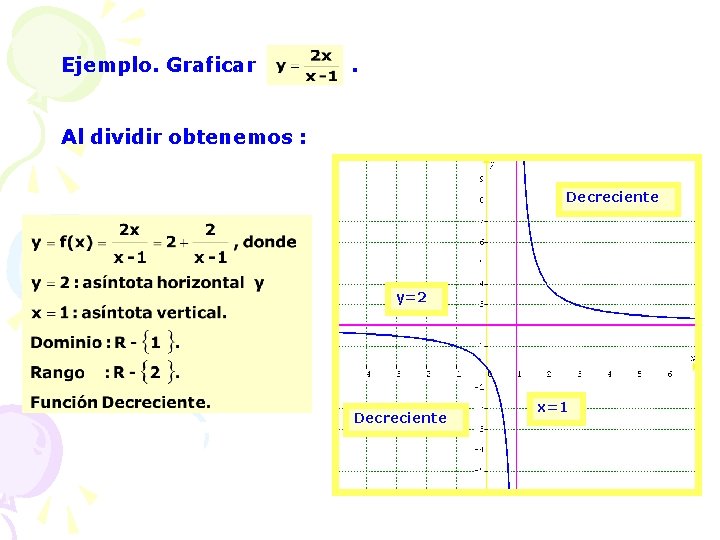
Ejemplo. Graficar . Al dividir obtenemos : Decreciente y=2 Decreciente x=1

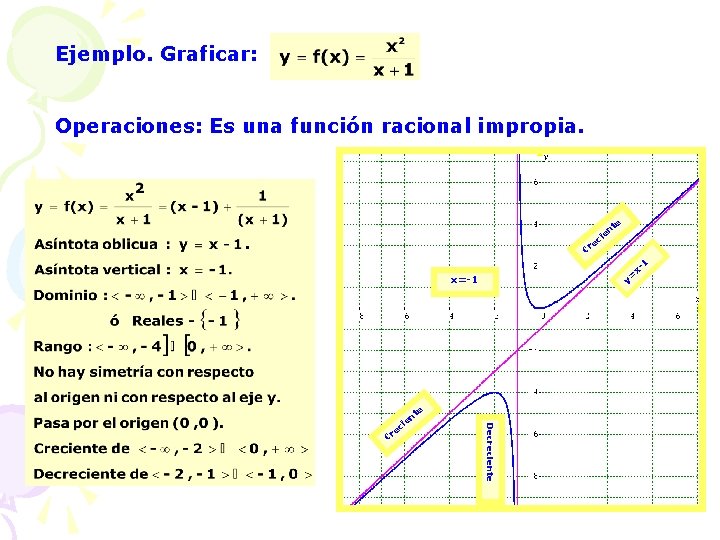
Ejemplo. Graficar: . Operaciones: Es una función racional impropia. e ci e nt e Cr 1 x= y x=-1 e e Cr Decreciente nt e ci

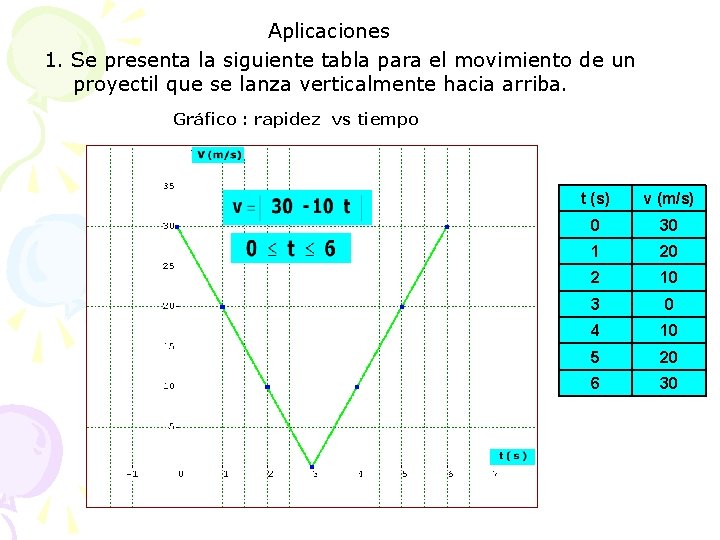
Aplicaciones 1. Se presenta la siguiente tabla para el movimiento de un proyectil que se lanza verticalmente hacia arriba. Gráfico : rapidez vs tiempo t (s) v (m/s) 0 30 1 20 2 10 3 0 4 10 5 20 6 30

2. Se presenta la siguiente tabla para el movimiento de un proyectil que se lanza verticalmente hacia arriba. Gráfico : Velocidad vs Tiempo V t (s) t v (m/s) 0 30 1 20 2 10 3 0 4 -10 5 -20 6 -30

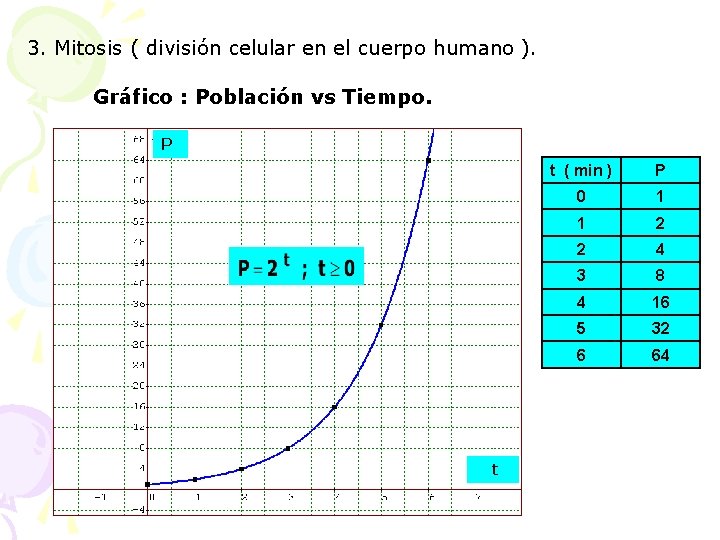
3. Mitosis ( división celular en el cuerpo humano ). Gráfico : Población vs Tiempo. P t t ( min ) P 0 1 1 2 2 4 3 8 4 16 5 32 6 64

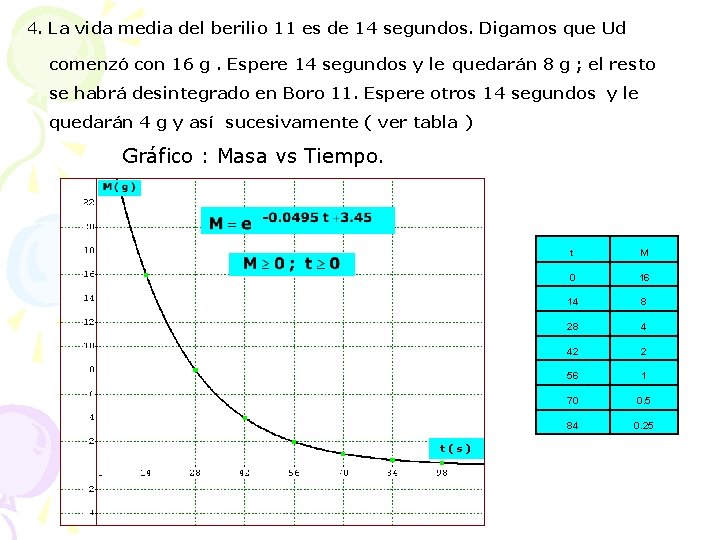
4. La vida media del berilio 11 es de 14 segundos. Digamos que Ud comenzó con 16 g. Espere 14 segundos y le quedarán 8 g ; el resto se habrá desintegrado en Boro 11. Espere otros 14 segundos y le quedarán 4 g y así sucesivamente ( ver tabla ) Gráfico : Masa vs Tiempo. t(s) t M 0 16 14 8 28 4 42 2 56 1 70 0. 5 84 0. 25

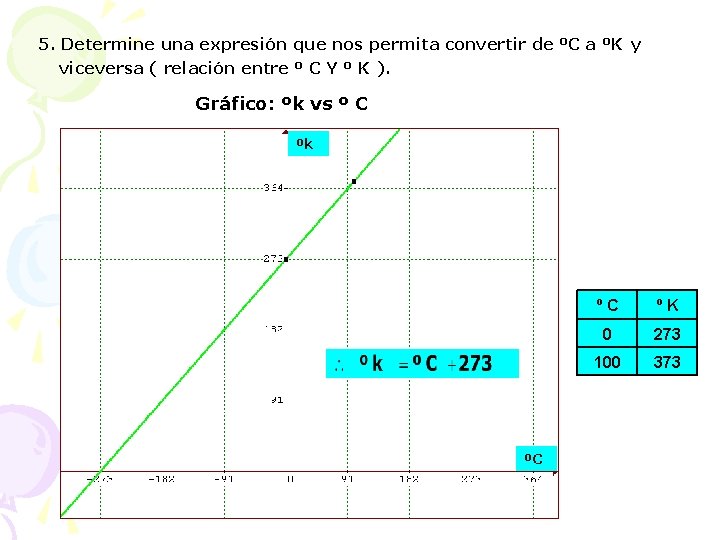
5. Determine una expresión que nos permita convertir de ºC a ºK y viceversa ( relación entre º C Y º K ). Gráfico: ºk vs º C ºk ºC ºC ºK 0 273 100 373

Cálculo de la pendiente : Si la temperatura cambia un grado en la escala Celsius , entonces en la escala Kelvin cambiará también un grado. Se conoce al menos un punto y la pendiente : entonces: ,

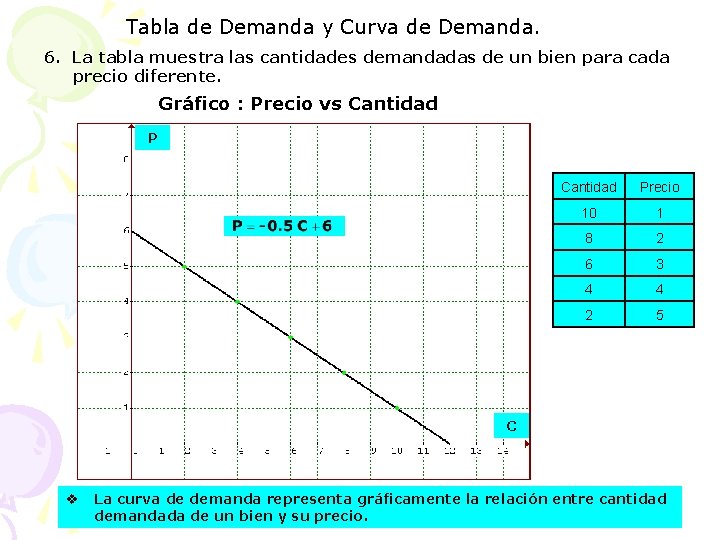
Tabla de Demanda y Curva de Demanda. 6. La tabla muestra las cantidades demandadas de un bien para cada precio diferente. Gráfico : Precio vs Cantidad Precio 10 1 8 2 6 3 4 4 2 5 C v La curva de demanda representa gráficamente la relación entre cantidad demandada de un bien y su precio.

LEY DEL ENFRIAMIENTO DE NEWTON Establece que la temperatura de un objeto caliente disminuye en forma exponencial con el tiempo hacia la temperatura del medio ambiente , mediante la siguiente expresión :

7. Un objeto caliente a 100°C se deja enfriar en un cuarto cuya temperatura del aire es de 30°C. Si la temperatura del objeto es de 80°C después de 5 minutos , ¿ en qué momento llegará a 50° C. Resolución. Datos :

Llegará a la temperatura de 50ºC después de 18. 6 minutos aproximadamente. v Se puede utilizar un programa o la GDC para comprobar lo desarrollado anteriormente.

Química : El p. H de una solución química está dado aproximadamente por la fórmula: donde es la concentración de iones de hidrógeno en moles por litro. Los valores de p. H varían de 0 (ácido) a 14 alcalino. 8. a) Determine el p. H del agua en un recipiente de 1 litro , con 0. 0000001 moles de iones de hidrógeno. b) Determine la concentración de iones de hidrógeno en una solución semiácida con un p. H 4. 2. Resolución.

Magnitud de un terremoto en la Escala de Richter Es una forma de convertir las lecturas sismográficas en números que proporcionen una referencia sencilla para medir la magnitud M de un terremoto. La escala que se utiliza es logarítmica. Todos los terremotos se comparan con un terremoto de nivel cero cuya lectura sismográfica mide 0. 001 mm a una distancia de 100 Km del epicentro. Un terremoto cuya lectura sismográfica mide x mm tiene una magnitud M (x) dada por : x 0 =10 -3 mm , lectura de terremoto de nivel cero a 100 km de distancia

9. ¿Cuál es la magnitud de un terremoto cuya lectura sismográfica es 0. 01 mm a una distancia de 100 km del epicentro? . Resolución. X = 0. 1 mm , x 0 = 0. 001 mm , M ( x= 0. 1 ) = ? ? El terremoto mide 2. 0 en la escala Richter y es 100 veces más intenso que el de nivel cero.

10. El devastador terremoto de San Francisco en 1906 midió 8. 9 en la escala Richter. ¿ Cómo se compara ese terremoto con el de Papúa , Nueva Guinea 1988 , midió 6. 7 en la misma escala. Rp. El terremoto de San Francisco fue 182 veces más intenso que el terremoto de Papúa , Nueva Guinea.