Sistemas Numricos Sistemas decimal binario octal y hexadecimal

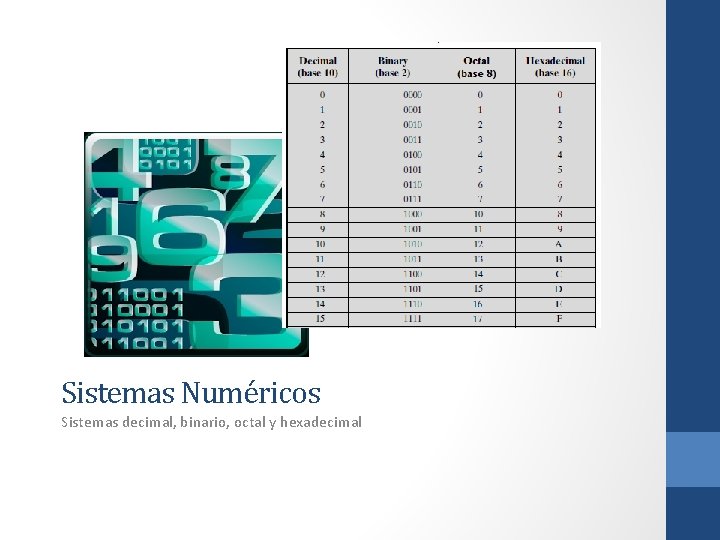
Sistemas Numéricos Sistemas decimal, binario, octal y hexadecimal

Sistemas Numéricos - Sistema Decimal En la vida cotidiana usamos el sistema decimal, basado en los dígitos decimales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 para representar números. Considere el significado del número 83. Este significa ocho decenas más tres unidades: 83 = (8 x 10) + 3 El número 4728 significa cuatro unidades de millar más siete centenas más dos decenas más ocho unidades. 4728 = (4 x 1000) + (7 x 100) + (2 x 10) + 8 Se dice que el sistema decimal tiene como base el número 10. Esto significa que cada dígito en el número es multiplicado por 10 elevado a la potencia correspondiente a la posición del dígito:

Sistemas Numéricos – Sistema Decimal El mismo principio se aplica para fracciones decimales, pero en este caso se usan potencias necativas de 10. Entonces, la fracción decimal 0. 256 significa 2 décimas más 5 centésimas más 6 milésimas: Un número con parte entera y parte fraccional tiene dígitos elevados tanto a potencias positivas como negativas de 10: En general, para la representación decimal del número X, en donde X tiene los dígitos el valor de X es

Sistemas Numéricos - Sistema Binario El sistema binario se utiliza en las computadoras, debido a que éstas trabajan internamente con dos niveles de voltaje (encendido 1, apagado 0). El sistema binario tiene solo dos dígitos 0 y 1. Por lo tanto, los números en sistema binario son representados en base 2. NOTA: Para evitar cualquier confusión al operar con distintas bases, la base correspondiente a un número se escribe a manera de subscrito. Por ejemplo, 8310 y 472810 son números representados en notación decimal o, más brevemente, números decimales. Los dígitos 1 y 0 en notación binaria tienen el mismo valor que los correspondientes en notación decimal: Para representar números más grandes, tal como en el caso de la notación decimal, cada dígito en un número binario tiene un valor que depende de su posición: y así sucesivamente.

Sistemas Numéricos - Sistema Binario Al igual que en el caso del sistema decimal, los valores fraccionales binarios se representan con potencias negativas de la base: NOTA: En ocasiones, cuando se convierte un número decimal a un número binario, la parte fraccional de un número decimal puede ser representada exactamente como fracción binaria, lo que significa que se requiere un número finito de bits en la parte fraccional binaria para expresar exactamente la parte fraccional decimal. Sin embargo, en otras ocasiones, no es posible obtener una representación exacta de la fracción decimal en fracción binaria mediante un número finito de bits, por lo que solo se puede obtener una representación cercana, pero no exacta. En estos casos, la precisión de la representación fraccional decimal en binario dependerá del número de bits utilizados. A mayor número de bits, mayor precisión para representar valores fraccionales decimales. En general, para un número binario Y, en donde Y tiene los dígitos: el valor de Y es

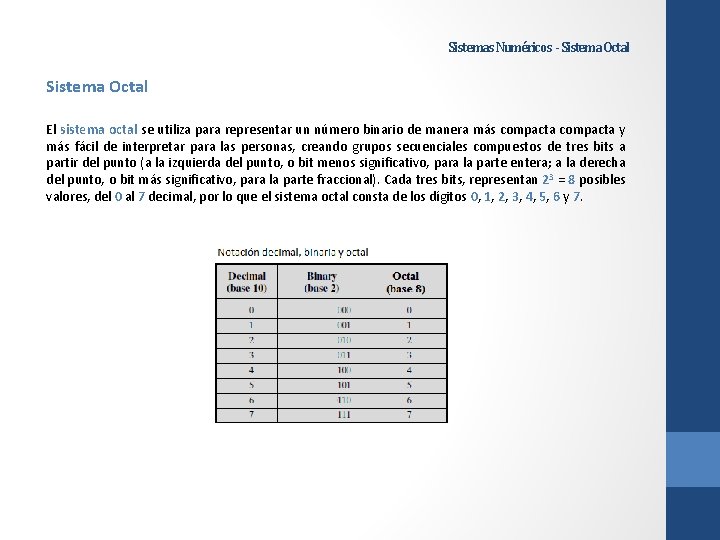
Sistemas Numéricos - Sistema Octal El sistema octal se utiliza para representar un número binario de manera más compacta y más fácil de interpretar para las personas, creando grupos secuenciales compuestos de tres bits a partir del punto (a la izquierda del punto, o bit menos significativo, para la parte entera; a la derecha del punto, o bit más significativo, para la parte fraccional). Cada tres bits, representan 23 = 8 posibles valores, del 0 al 7 decimal, por lo que el sistema octal consta de los dígitos 0, 1, 2, 3, 4, 5, 6 y 7.

Sistemas Numéricos - Sistema Octal El sistema octal tiene como base el número 8. Esto significa que cada dígito en el número es multiplicado por 8 elevado a la potencia correspondiente a la posición del dígito: En el primer ejemplo, se requirieron solo dos dígitos octales (128) en lugar de los cuatro dígitos binarios (10102) para representar el número diez decimal (1010). Esto es: 128 = (1 x 81) + (2 x 80) = 810 + 210 = 1010 En el segundo ejemplo, se requirieron solo tres dígitos octales (1448) en lugar de los siete dígitos binarios (11001002) para representar el número cien decimal (10010). Esto es: 1448 = (1 x 82) + (4 x 81) + (4 x 80) = 6410 + 3210 + 410 = 10010 NOTA: En el caso óptimo, no es necesario agregar ceros binarios a la izquierda para obtener un número de bits que sea múltiplo de 3 para agrupar los bits de tres en tres de manera exacta. En este caso, el número de dígitos octales será tres veces menor a los bits necesarios para representar el mismo número.

Sistemas Numéricos - Sistema Octal 12. 348 = (1 x 81) + (2 x 80) + (3 x 8 -1) + (4 x 8 -2) = 810 + 210 + 0. 37510 + 0. 062510 = 10. 4375 10

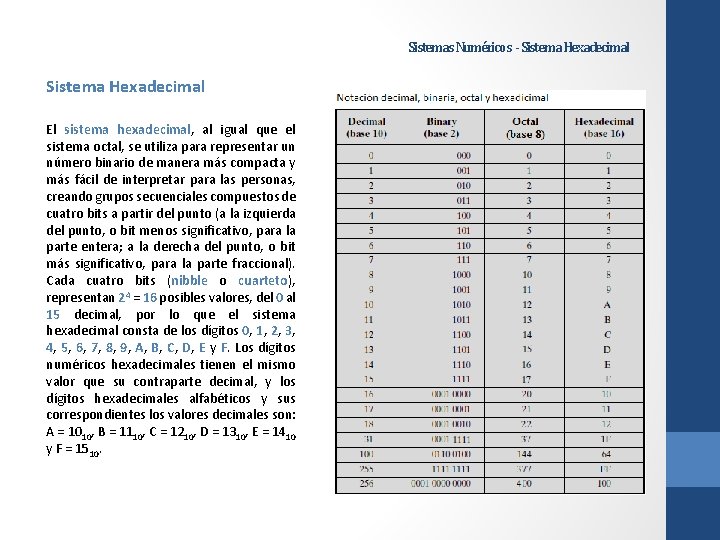
Sistemas Numéricos - Sistema Hexadecimal El sistema hexadecimal, al igual que el sistema octal, se utiliza para representar un número binario de manera más compacta y más fácil de interpretar para las personas, creando grupos secuenciales compuestos de cuatro bits a partir del punto (a la izquierda del punto, o bit menos significativo, para la parte entera; a la derecha del punto, o bit más significativo, para la parte fraccional). Cada cuatro bits (nibble o cuarteto), representan 24 = 16 posibles valores, del 0 al 15 decimal, por lo que el sistema hexadecimal consta de los dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Los dígitos numéricos hexadecimales tienen el mismo valor que su contraparte decimal, y los dígitos hexadecimales alfabéticos y sus correspondientes los valores decimales son: A = 1010, B = 1110, C = 1210, D = 1310, E = 1410 y F = 1510.

Sistemas Numéricos - Hexadecimal El sistema hexadecimal tiene como base el número 16. Esto significa que cada dígito en el número es multiplicado por 16 elevado a la potencia correspondiente a la posición del dígito: NOTA: Es común utilizar la h o H en lugar del subscrito 16 para especificar un número hexadecimal, o también se puede usar el prefijo 0 x ante el número hexadecimal. En el primer ejemplo, se requirieron solo dos dígitos hexadecimales (1 F 16 o 1 Fh) en lugar de los cinco dígitos binarios (11111 2) para representar el número 31 decimal (31 10). Esto es: 1 F 16 = 1 Fh = 1 FH = 0 x 1 F = (1 x 161) + (15 x 160) = 1610 + 1510 = 3110 En el segundo ejemplo, se requirieron solo dos dígitos hexadecimales (648) en lugar de los siete dígitos binarios (11001002) para representar el número cien decimal (10010). Esto es: 6416 = 64 h = 64 H = 0 x 64 = (6 x 16 1) + (4 x 160) = 9610 + 410 = 10010 NOTA: En el caso óptimo, no es necesario agregar ceros binarios a la izquierda para obtener un número de bits que sea múltiplo de 4 para agrupar los bits de cuatro en cuatro de manera exacta. En este caso, el número de dígitos hexadecimales será cuatro veces menor a los bits necesarios para representar el mismo número.

Sistemas Numéricos - Sistema Hexadecimal 1 A. 28 h = (1 x 161) + (10 x 160) + (2 x 16 -1) + (8 x 16 -2) = 1610 + 1010 + 0. 062510 + 0. 0312510 = 26. 1562510

Sistemas Numéricos - Conversiones – binario a decimal Conversiones Binario a Decimal Es simple convertir un número en notación binaria a un número en notación decimal. La metodología ya la hemos usado en los ejemplos anteriores. Todo lo que se requiere es multiplicar cada dígito binario por su potencia de 2 correspondiente y sumar los resultados obtenidos para cada bit. Si el número binario se representa como El número decimal correspondiente será

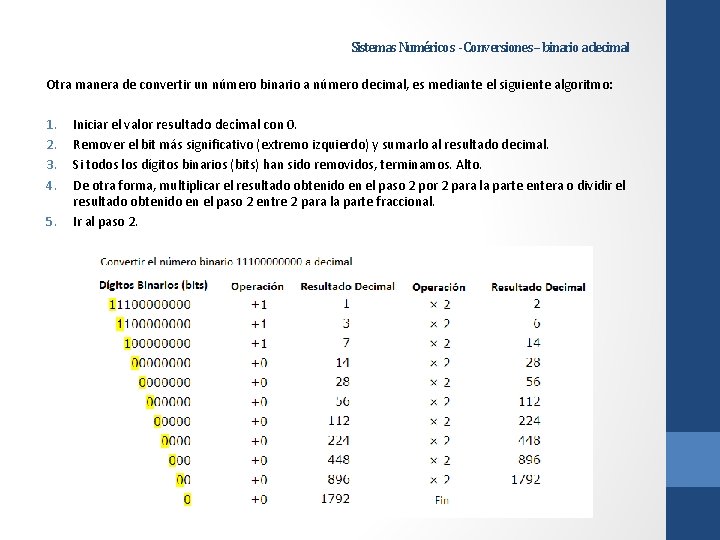
Sistemas Numéricos - Conversiones – binario a decimal Otra manera de convertir un número binario a número decimal, es mediante el siguiente algoritmo: 1. 2. 3. 4. 5. Iniciar el valor resultado decimal con 0. Remover el bit más significativo (extremo izquierdo) y sumarlo al resultado decimal. Si todos los dígitos binarios (bits) han sido removidos, terminamos. Alto. De otra forma, multiplicar el resultado obtenido en el paso 2 por 2 para la parte entera o dividir el resultado obtenido en el paso 2 entre 2 para la parte fraccional. Ir al paso 2.

Sistemas Numéricos - Conversiones – decimal a binario Decimal a Binario La conversión de un número decimal entero a binario se efectúa mediante divisiones entre dos de manera repetitiva. Los residuos y el cociente final, 1, proporcionan, en orden de creciente significancia, los dígitos binarios de la representación en base 2 del número en base 10.

Sistemas Numéricos - Conversiones – decimal a binario

Sistemas Numéricos - Conversiones – decimal a binario La conversión de un número decimal fraccional a binario se efectúa considerando que un número binario fraccional tiene la forma y tiene valor Esto puede reescribirse como Esta expresión sugiere un método de conversión de decimal a binario de una fracción. Supóngase que se desea convertir el número F (0 < F < 1) de notación decimal a notación binaria. F puede escribirse como Si se multiplica F por 2, se obtiene Se puede observar que la parte entera de 2 x F, la cual puede ser 0 o 1 porque 0 < F < 1, es simplemente b-1. Entonces, se puede decir que 2 x F = b-1 + F 1 , donde 0 < F 1 < 1 y

Sistemas Numéricos - Conversiones – decimal a binario Para encontrar b-2 , se repite el proceso. Por lo tanto, el algoritmo de conversión involucra la multiplicación por 2 de manera repetitiva. En cada paso, la parte fraccional del número de la etapa anterior se multiplica por 2. El dígito a la izquierda del punto decimal en el producto será 0 o 1 y contribuye a la representación binaria de la fracción decimal, empezando con el bit más significativo. La parte fraccional del producto es usada como multiplicando del siguiente paso. NOTA: Este procedimiento no es necesariamente exacto; esto es, una fracción decimal con un número finito de dígitos podría requerir una fracción binaria con un número infinito de dígitos. En tales casos, el algoritmo de conversión es usualmente detenido después un número específico de pasos, dependiendo de la exactitud deseada.

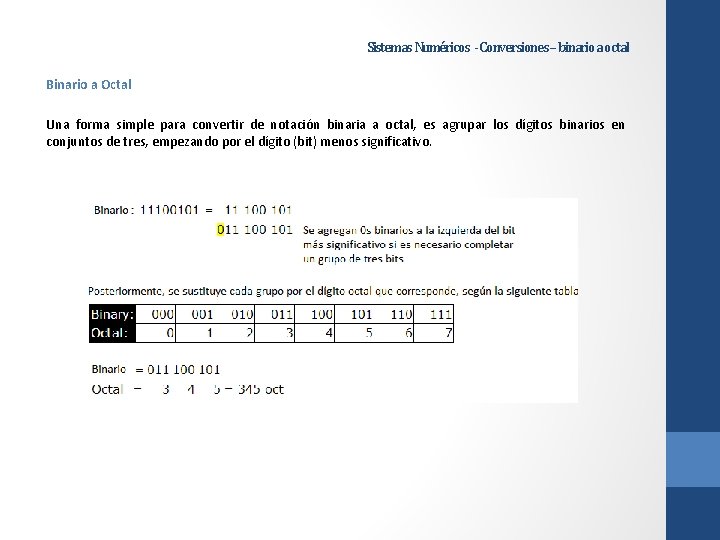
Sistemas Numéricos - Conversiones – binario a octal Binario a Octal Una forma simple para convertir de notación binaria a octal, es agrupar los dígitos binarios en conjuntos de tres, empezando por el dígito (bit) menos significativo.

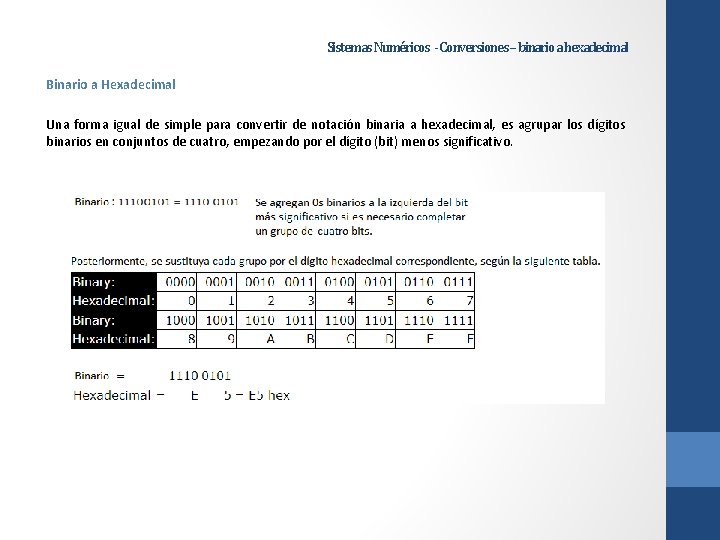
Sistemas Numéricos - Conversiones – binario a hexadecimal Binario a Hexadecimal Una forma igual de simple para convertir de notación binaria a hexadecimal, es agrupar los dígitos binarios en conjuntos de cuatro, empezando por el dígito (bit) menos significativo.

Sistemas Numéricos - Conversiones – decimal a octal Decimal a Octal El método para convertir de notación decimal a octal se presenta mediante la división entre 8 de manera repetitiva, tal como se muestra en el siguiente ejemplo: Conversión del número 1792

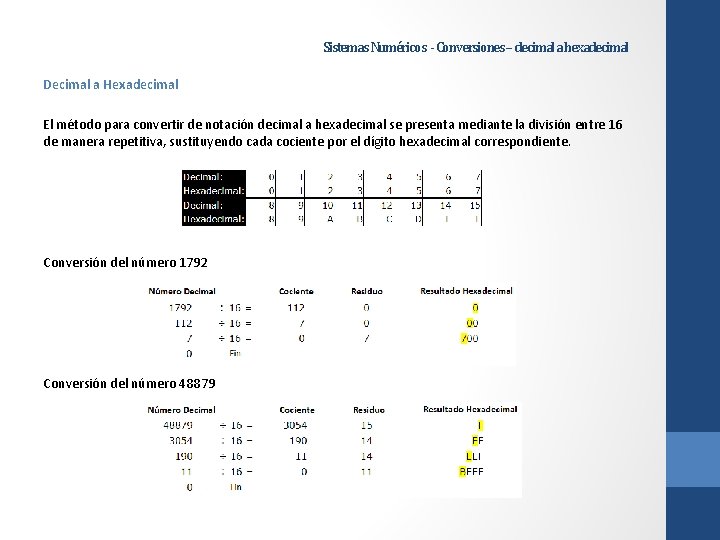
Sistemas Numéricos - Conversiones – decimal a hexadecimal Decimal a Hexadecimal El método para convertir de notación decimal a hexadecimal se presenta mediante la división entre 16 de manera repetitiva, sustituyendo cada cociente por el dígito hexadecimal correspondiente. Conversión del número 1792 Conversión del número 48879

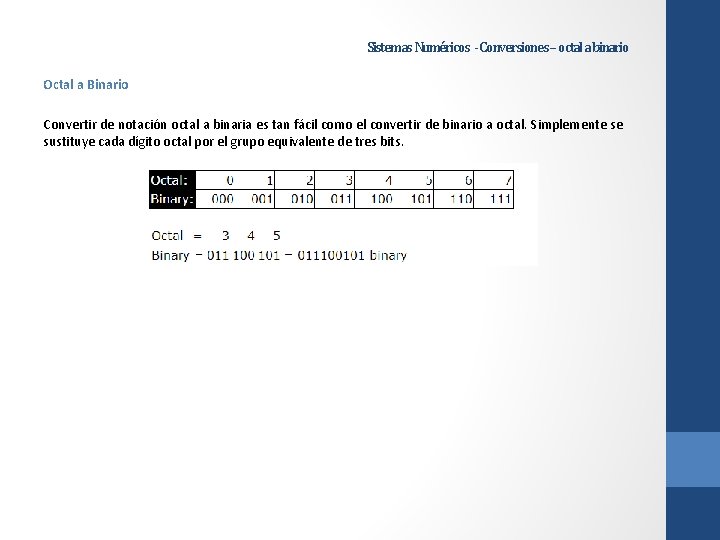
Sistemas Numéricos - Conversiones – octal a binario Octal a Binario Convertir de notación octal a binaria es tan fácil como el convertir de binario a octal. Simplemente se sustituye cada dígito octal por el grupo equivalente de tres bits.

Sistemas Numéricos - Conversiones – octal a hexadecimal Octal a Hexadecimal Cuando se convierte de notación octal a hexadecimal, resulta más fácil convertir primeramente el número octal a binario y después de binario a hexadecimal. Por ejemplo, para convertir el número 3458 a hexadecimal:

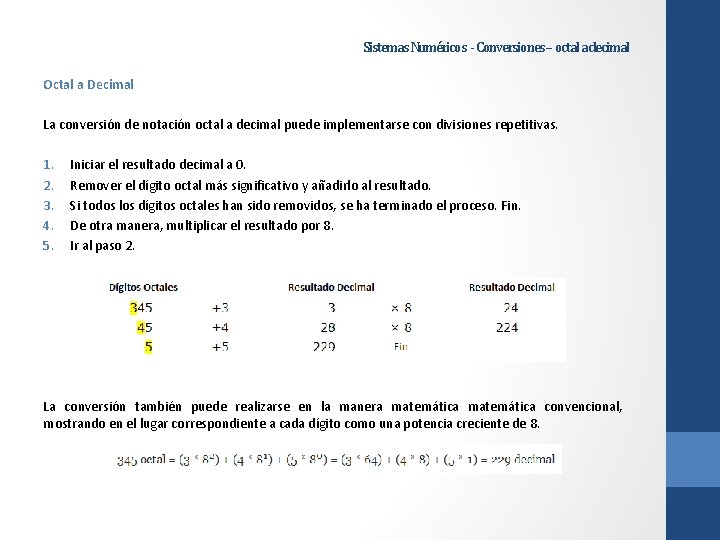
Sistemas Numéricos - Conversiones – octal a decimal Octal a Decimal La conversión de notación octal a decimal puede implementarse con divisiones repetitivas. 1. 2. 3. 4. 5. Iniciar el resultado decimal a 0. Remover el dígito octal más significativo y añadirlo al resultado. Si todos los dígitos octales han sido removidos, se ha terminado el proceso. Fin. De otra manera, multiplicar el resultado por 8. Ir al paso 2. La conversión también puede realizarse en la manera matemática convencional, mostrando en el lugar correspondiente a cada dígito como una potencia creciente de 8.

Sistemas Numéricos - Conversiones – hexadecimal a binario Hexadecimal a Binario Convertir de notación hexadecimal a binaria es tan fácil como el convertir de binario a hexadecimal. Simplemente se sustituye cada dígito hexadecimal por el grupo equivalente de cuatro bits.

Sistemas Numéricos - Conversiones – hexadecimal a octal Hexadecimal a Octal Cuando se convierte de notación hexadecimal a octal, resulta más fácil convertir primeramente el número hexadecimal a binario y después de binario a octal. Por ejemplo, para convertir el número A 2 DEh a octal:

Sistemas Numéricos - Conversiones – hexadecimal a decimal Hexadecimal a Decimal El convertir un número en notación hexadecimal a decimal puede implementarse en la forma matemática convencional, mostrando cada posición de un dígito como una potencia creciente de 16. Claro está, los dígitos hexadecimales alfabéticos (letras) requieren ser convertidos a sus valores decimales correspondientes antes de efectuar las matemáticas.

Sistemas Numéricos - Qué Sistema Numérico Usar? El sistema numérico apropiado para representar un valor depende de la aplicación y la forma o formato en que se presentan los datos. Cada sistema numérico tiene sus ventajas y desventajas. Claro está, el sistema numérico que naturalmente todas las personas usan de manera cotidiana, el es sistema decimal. Las computadoras modernas tienen suficiente memoria y espacio de disco para los programas a usar. Sin embargo, muchos microcontroladores de baja capacidad pueden tener serias limitaciones de espacio. El proporcionar como salida un número decimal a un puerto serial o a un display, requiere que el número sea dividido por entre 10 para separar cada dígito. Dependiendo de las capacidades del microcontrolador, la rutina de división entre 10 por sí misma puede requerir más espacio que una rutina de salida hexadecimal. Cuando se diagnóstica un problema de en la salida de un pin de un puerto, es preferible observar las salidas de los pins del puerto en forma binaria. Lo mismo es cierto cuando se requiere conocer los valores de banderas en registros o memoria. La desventaja es que la longitud de la notación binaria crece muy rápidamente. Cuando se depura (debugging) la memoria, discos o flujos de datos en microcontroladores o computadoras, la notación hexadecimal provee un formato compacto que es fácil de organizar en bytes y convertir en bits. El sistema octal ha perdido popularidad en los últimos 30 años, ya que es difícil encontrar microcontroladores o microprocesadores que operen con datos con longitudes en bits que sean múltiplos de 3. La ventaja del sistema octal es que solo usa dígitos numéricos, a diferencia del sistema hexadecimal que utiliza también dígitos alfabéticos. NOTA: Parte importante de las notas y gráficas para mostrar los distintos sistemas numéricos y las conversiones entre sistemas numéricos están basadas o tomadas de la página www. robotroom. com.