Un contexto ptimo para las series de Fourier

Un contexto óptimo para las series de Fourier. Presentación del proyecto.

Teoría de la señal. • En telecomunicaciones (y cualquier otra ingeniería) existe una disciplina que brilla con luz propia: la teoría de la señal. • Esta teoría se basa en el Análisis Funcional, aunque con una orientación claramente más práctica. • Estudiar teoría de señales implica inevitablemente estudiar análisis de Fourier.

Idea raíz del proyecto. • La idea principal consiste en incentivar el estudio del Análisis de Fourier a través de la tarea de encontrar un “hogar cómodo” para las series de Fourier. • La estructura se divide en tres capítulos: – Series y coeficientes de Fourier. – Series de Fourier y problemas de contorno. – Un contexto óptimo para las series de Fourier.

Breve introducción histórica. • Período “Euler-Bernoulli-D`Alambert”: – Basan sus conclusiones en el estudio de la cuerda vibrante. Experimentalmente se prueba que ciertos tipos de oscilaciones se pueden expresar como – Determinar si la función que se pretendía representar por medio de una serie trigonométrica podría ser cualquiera o no.

Breve introducción histórica. • Período de Fourier: – Cualquier función definida sobre el intervalo [0, 2 pi] se puede representar como una serie de senos y cosenos. • Período posterior a Fourier: – Se estrecha el filtro de funciones analizables por Fourier. Contribuye especialmente a fijar estas condiciones, Dirichlet. – La idea de Fourier incentiva el trabajo de muchos otros matemáticos como Riemann o Lebesgue.

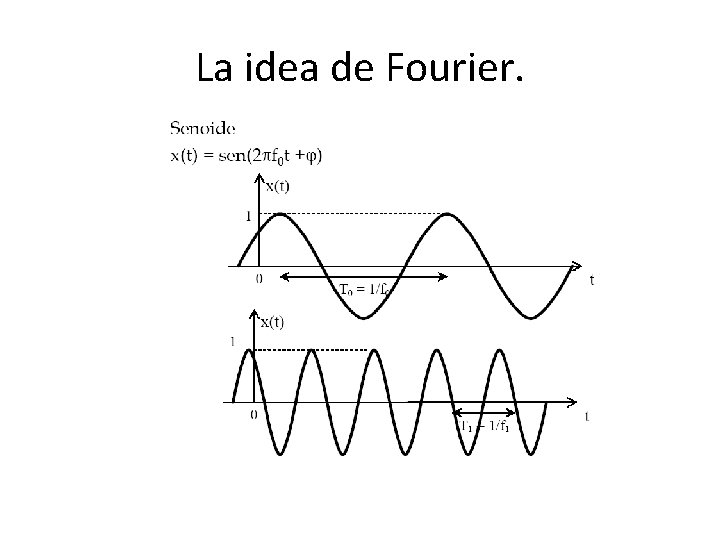
La idea de Fourier. • A comienzos del siglo XIX y mientras estudiaba problemas relacionados con la transmisión de calor, Fourier encuentra una manera de alcanzar la solución expresando las funciones por medio de sinusoides. • Las principales razones que le llevan a esto son: – Ser fáciles de derivar e integrar. – Poseer un ciclo extremadamente sencillo.

La idea de Fourier. • Así, toda función debería poder expresarse (según Fourier) como: • Esta expresión es la síntesis de Fourier y permite expresar una función en términos de sinusoides.

La idea de Fourier.

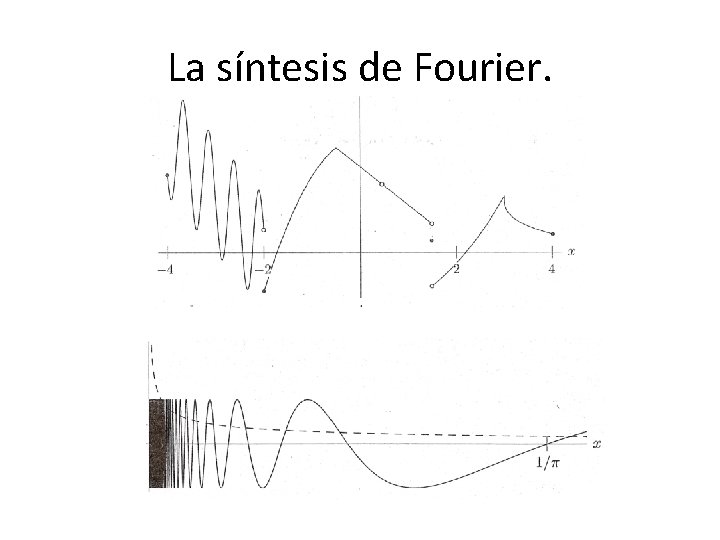
La síntesis de Fourier. • Para el caso 2 pi-periódico, la síntesis queda como: • Los coeficientes (fórmulas de análisis) quedan: • Un requisito que tiene que cumplir la función es ser continua a trozos.

La síntesis de Fourier. • Una función definida en un intervalo acotado es continua a trozos cuando: – Los límites laterales existen para todo punto del intervalo. – Los límites laterales derecho e izquierdo existen en los extremos respectivos del intervalo. – Contiene sólo un número finito de discontinuidades finitas en dicho intervalo.

La síntesis de Fourier.

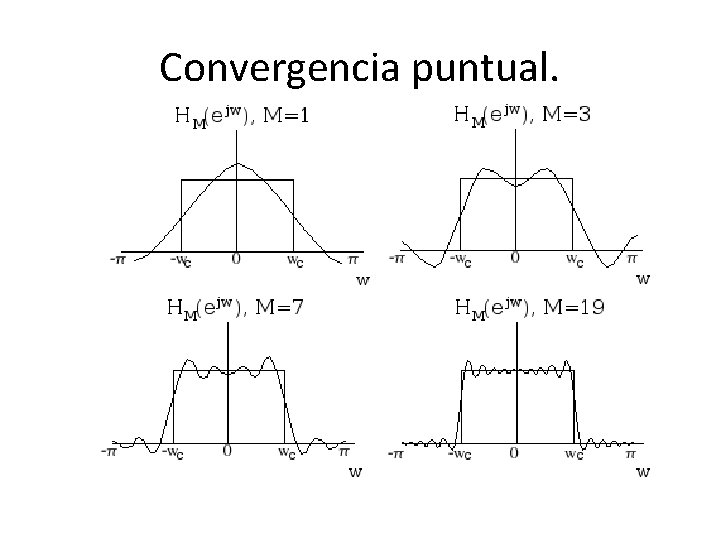
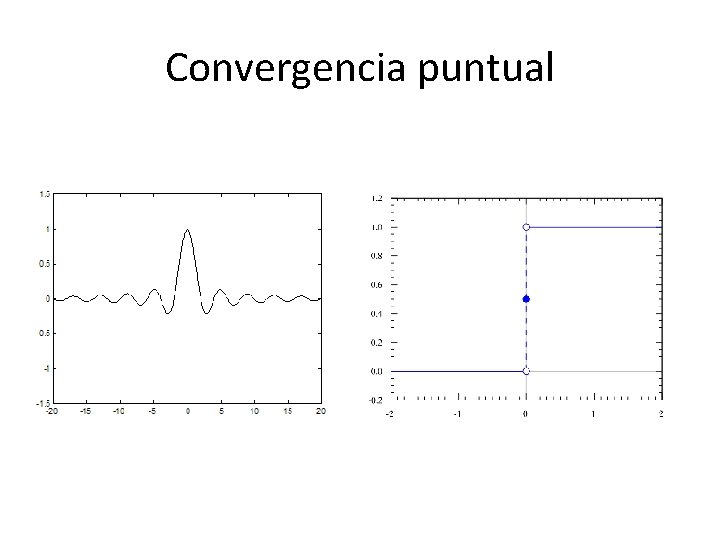
Convergencia puntual. • Ya sabemos qué condiciones tiene que cumplir la función para que los coeficientes existan. • El siguiente paso es analizar los requisitos que hacen que la serie converja. • Uno de los matemáticos que más aporta a este respecto es P. G. L. Dirichlet en 1829. • El estudio de estos requisitos lleva a una definición más precisa de función que la empleada en tiempos de Fourier.

Convergencia puntual. • El Lema de Riemann-Lebesgue asegura que para una función continua a trozos, se verifica: • Si además, los límites izquierdo y derecho de la derivada existen, entonces:

Convergencia puntual.

Convergencia puntual. • El espacio óptimo con este criterio de convergencia es el de las funciones suaves a trozos. • Una función es suave a trozos si tanto ella como su derivada son continuas a trozos en un cierto intervalo cerrado. • Además, se dice que la función es promediada si en cada punto del intervalo se cumple

Convergencia puntual

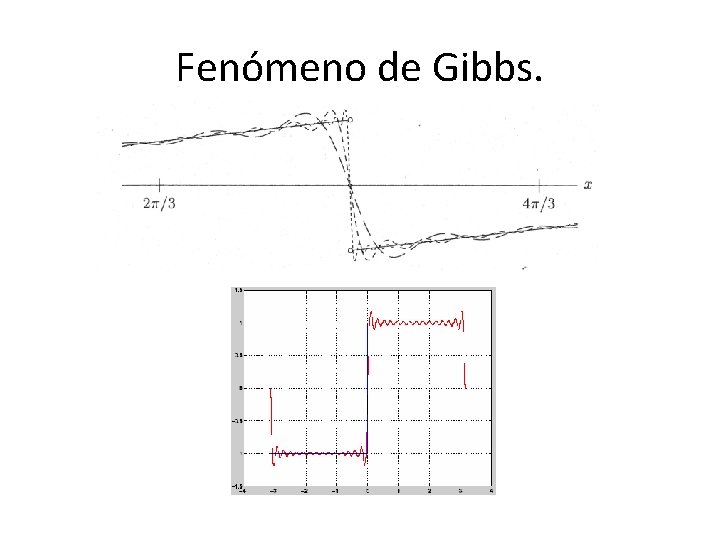
Fenómeno de Gibbs • A principios del siglo XX, el científico Gibbs descubre mediante un analizador de espectros un comportamiento extraño de las sumas parciales que aproximaban la función diente de sierra. • No se perdía la convergencia puntual, pero el comportamiento de la misma no era uniforme: en los puntos cercanos a la discontinuidad variaba de forma significativa.

Fenómeno de Gibbs.

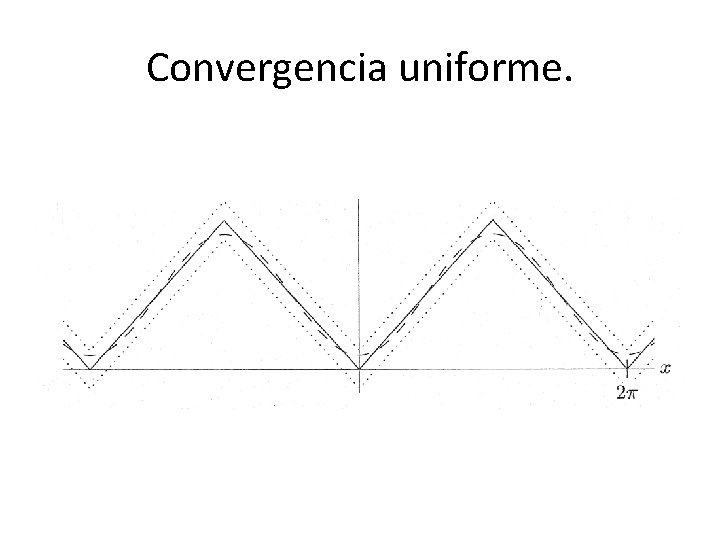
Convergencia uniforme. • Incluso trabajando con las funciones promediadas y suaves a trozos, sigue sin desaparecer el comportamiento anómalo en los puntos de discontinuidad. • Entonces el problema está en el criterio. Ahora se busca mantener la suma parcial dentro de un tubo tan pequeño como se quisiese: convergencia uniforme.

Convergencia uniforme. • Se dice que una sucesión converge uniformemente a una función f(x) si • La convergencia uniforme también implica convergencia puntual: es un criterio más restricitivo.

Convergencia uniforme. • Nos interesa tener las sumas parciales tan cerca de la función como se desee en todos los puntos sin distinción. • Ahora el interés es mantener la señal controlada en todo momento. • El espacio óptimo para este criterio es el de las funciones continuas y suaves a trozos.

Convergencia uniforme. • Hasta ahora los espacios que hemos analizado verifican: • Entre las ventajas de este criterio están la conservación de la continuidad y la garantía de la existencia de los coeficientes de Fourier de la serie asociada a la derivada de f.

Convergencia uniforme.

Problemas de contorno. • Comprobamos la efectividad de la descomposición sinusoidal en dos contextos: – La difusión del calor en cuerpos sólidos. – La propagación de ondas mecánicas. • Estos problemas, denominados de contorno constan de dos partes diferenciadas: – Ecuación en derivadas parciales. – Condiciones de contorno.

Problemas de contorno. • Fourier se vale de dos herramientas además de su método: – Separación de variables. – Principio de superposición. • La resolución de múltiples problemas siempre lleva a una serie de sinusoides, lo que constata la solidez del método.

Lámina metálica.

Lámina metálica. • La solución del problema homogéneo es • Esto implica que la derivada (doble) tiene que poder intercambiarse con la serie. • Por ello se exige una convergencia de cierta calidad: la convergencia uniforme.

Lámina metálica. • Para obtener la solución total, basta con hacer el análisis de Fourier de f(x): • La solución tiene además calidad: son continuas en el contorno del problema. • El método funciona en muchos otros casos: – Barra metálica, anillo, etc…

La simetría espacial. • Los sinusoides resultan ser óptimos en el modelado de múltiples problemas útiles. • La causa es la simetría espacial propia de muchos de estos problemas: – Un operador lineal es espacialmente simétrico si el resultado de rotar o trasladar las coordenadas y posteriormente aplicar el operador es idéntico a si se procede en sentido inverso. – La ecuación de Laplace es un caso.

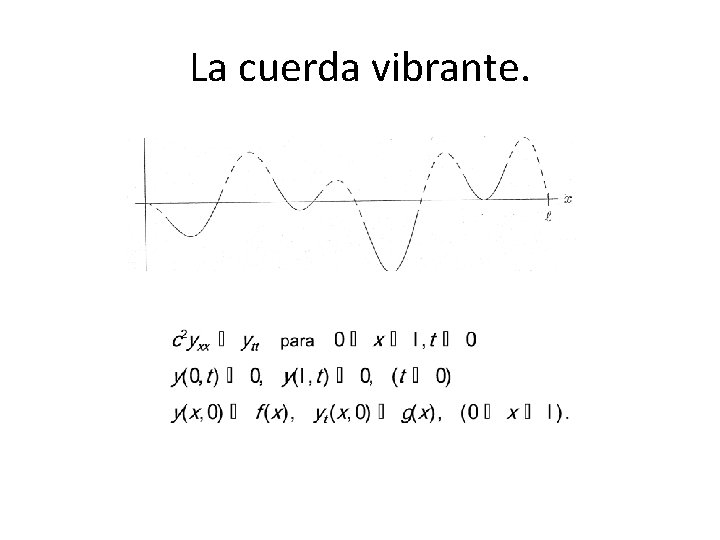
La ecuación de ondas. • También el método de Fourier demuestra aquí su utilidad. • La ecuación de ondas establece que la aceleración es proporcional a la concavidad. • Una manera sencilla de estudiar esta ecuación es con el modelo de la cuerda vibrante.

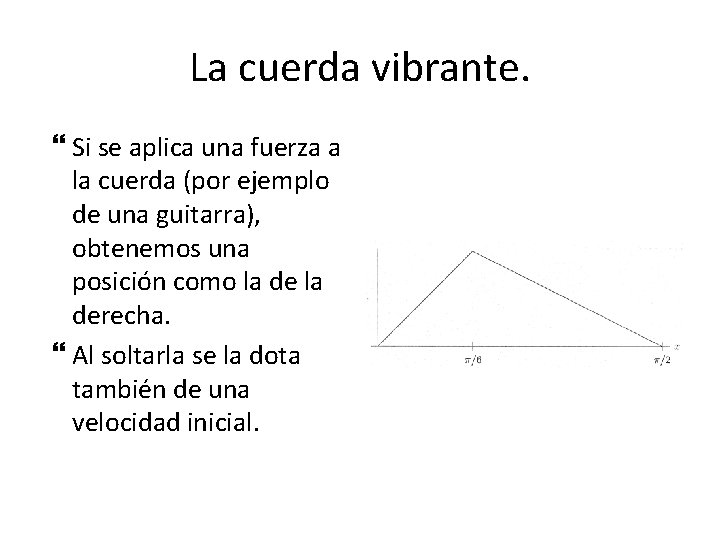
La cuerda vibrante. Si se aplica una fuerza a la cuerda (por ejemplo de una guitarra), obtenemos una posición como la derecha. Al soltarla se la dota también de una velocidad inicial.

La cuerda vibrante.

La cuerda vibrante. • De nuevo llegamos a una solución del tipo serie de Fourier: • Es imprescindible la convergencia uniforme para poder soportar las dos derivadas espaciales y temporales. • El resto se obtiene con análisis de Fourier.

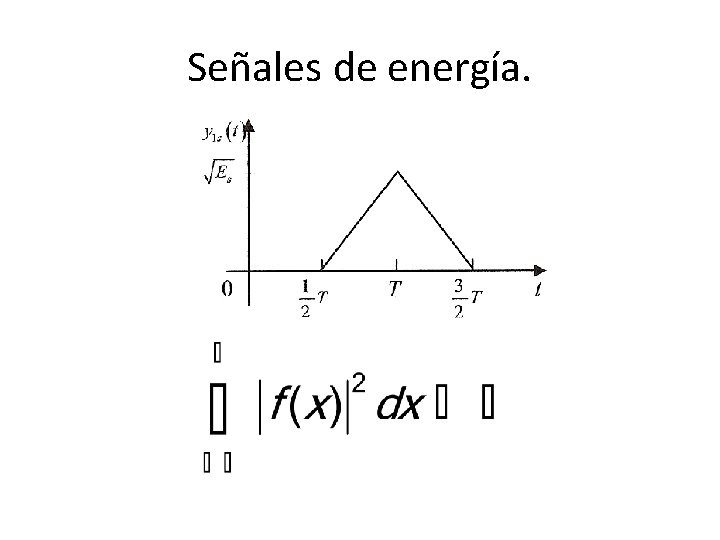
Señales de energía. • Introducimos ahora un nuevo criterio de convergencia: convergencia en norma. • El espacio óptimo con este criterio será el de las funciones de cuadrado sumable. • A las funciones de cuadrado sumable se las llama también de energía. • Modelan fenómenos tan dispares como la trasmisión de potencia eléctrica o la aplicación de una fuente de calor.

Señales de energía.

La norma cuadrática media. • La convergencia uniforme decía: • El supremo se usa para medir la magnitud de una función. En el caso de la convergencia uniforme, se está midiendo la distancia entre la suma enésima y la función en el límite.

La norma cuadrática media. • Pero el supremo no es la única manera de hacer esto, ni tampoco la más adecuada. • Un indicador más adecuado sería la norma cuadrática media: • Esta norma permite el uso de la geometría para trabajar con la funciones.

La norma cuadrática media. • El espacio C(T) es normado. Otros ejemplos de espacios normados son: – El espacio euclídeo n-dimensional con – El conjunto de las funciones acotadas en los números reales, B(A, R) cuya norma es

Convergencia en norma. • Dada una sucesión de funciones fn y una función f, si se cumple entonces se dice que la sucesión converge a la función en norma cuadrática media. • Esta expresión está diciendo que la distancia entre dos elementos del espacio normado puede hacerse tan pequeña como se desee sin más que ir aumentando el número de términos.

Relación entre convergencias. • Convergencia uniforme implica convergencia en norma y puntual. • Convergencia puntual y en norma no mantienen una relación tan clara. • Ejemplo: dada una sucesión en C(T) definida por, ésta converge a la función nula puntualmente pero no en norma.

Relación entre convergencias.

El producto interior. • Junto con la norma permite el contexto geométrico, proporcionando la noción de ángulo. • Para dos funciones f y g pertenecientes a C(T), se corresponde con • Se trata de una versión generalizada del producto escalar euclídeo.

Espacios completos. • Cuando se trabaja convergencia, una de las mejores noticias que nos pueden dar es que el espacio con el que se trabaje sea completo. • Mientras que conceptos como sucesión monótona y supremo no tienen sentido una vez se pierde el orden, la caracterización de la completitud sí lo tiene.

Espacios completos. • Un espacio completo es aquel en el que toda sucesión de Cauchy es convergente. • Un ejemplo de espacio completo es el euclídeo Rn. Por desgracia, C(T) no lo es. • En un espacio completo resulta más sencillo determinar la convergencia de una sucesión.

Pseudométrica y métrica. • Una pseudométrica sobre un cierto conjunto X es una regla que asocia a un par de elementos x e y de dicho espacio, un número real no negativo d(x, y) con las propiedades: – El valor d(x, y) es igual que d(y, x). – El valor d(x, z) es menor o igual que d(x, y)+d(y, z). • Si además, se verifica que d(x, y) implica x=y, entonces se califica al espacio como métrico.

Sucesiones de Cauchy. • Una sucesión de Cauchy es aquella cuyos elementos x 1, x 2… están formados a partir de un determinado espacio métrico o pseudométrico y verifican • Toda sucesión definida sobre un espacio métrico (X, d) es de Cauchy.

Sucesiones de Cauchy. • Un ejemplo de sucesión de Cauchy en el spacio de los números racionales positivos es • Un ejemplo de sucesión que no es de Cauchy en el espacio de los números racionales es

Sucesiones de Cauchy. • Puede definirse un espacio completo como aquel en el que toda sucesión de Cauchy contenida en el mismo converge también a un elemento del mismo, o lo que es igual • Si nos garantizan que un espacio es completo y podemos saber si la sucesión es de Cauchy, entonces convergerá seguro. • Un espacio es completo si no tiene huecos.

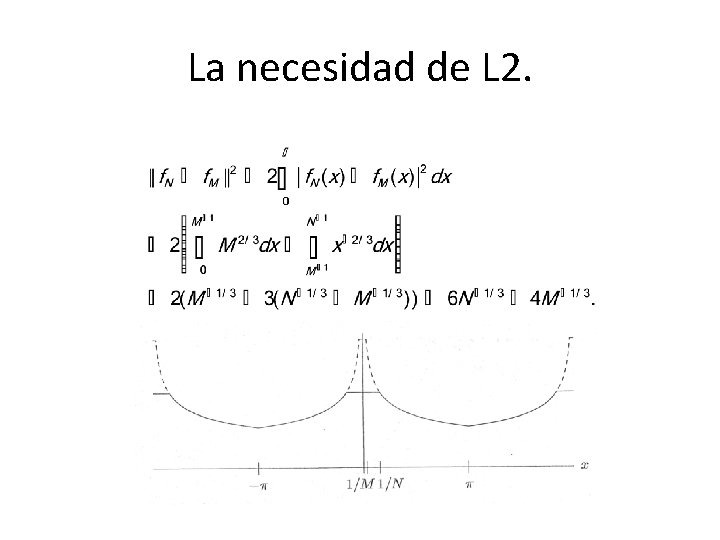
La necesidad de L 2. • El espacio C(T) no es completo con respecto a la norma cuadràtica media. • Dada la sucesión de funciones no converge en norma a ninguna función de C(T).

La necesidad de L 2.

La necesidad de L 2. • El resultado de este límite es la función • Esta función no tiene límite en el origen. Por tanto no es C(T) ni tan siguiera PC(T). • Debe existir otra espacio en el que las sucesiones de Cauchy encuentren siempre un sumidero para converger.

La necesidad L 2. • En C(T) se nos presenta un problema grave: – El límite puntual no existe siempre dentro de C(T). • Para solucionarlo, aceptaremos el límite anterior siempre y cuando se cumpla en todo salvo en conjuntos de media nula, i. e, en casi todo.

Concepto de realización. • Una función f es la realización de una sucesión fn si se cumple “en casi todo”: • Dada una sucesión de funciones h 1, h 2… en C(T), llamamos sucesión de ultra. Cauchy a la que verifique (para c positivo y k entero positivo):

El espacio L 2 • El espacio formado por todas las realizaciones de sucesiones de ultra. Cauchy en C(T) es el de funciones de cuadrado sumable o también llamado L 2. • Entre sus propiedades más interesantes están: – C(T) es denso en L 2(T). – La norma es igual al limite en norma. – Los elementos de L 2(T) tienen norma cuadratica media.

El espacio L 2. • El espacio L 2(T) está dotado, además de con una norma, de un producto interior: • Esto posibilita disponer de un marco geométrico para el estudio, al igual que con C(T), teniendo además ahora la ventaja de estar trabajando en un espacio completo.

El espacio L 1. • Otro espacio especialmente interesante es el formado por funciones que verifican donde la integral es la de Lebesgue. • Los elementos de L 1(T) se obtienen multiplicando elementos de L 2(T).

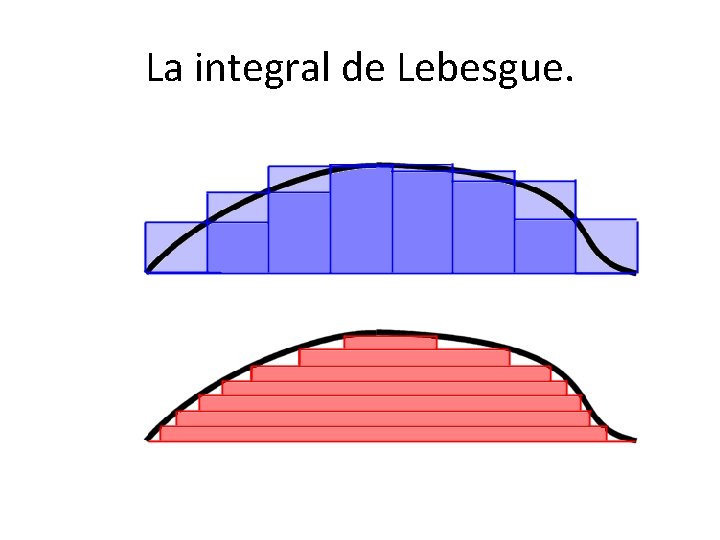
La integral de Lebesgue. • La integración de Lebesgue es más general que la de Riemann. • Lebesgue hace la partición en el eje dependiente, siendo los conjuntos resultantes en el independiente raros en general. • Es aplicable a un mayor número de funciones. • En análisis de Fourier, algunas funciones no son claramente integrables Riemann.

La integral de Lebesgue.

El problema de L 1. • El espacio L 1 está formado, al igual que L 2 por realizaciones de funciones continuas. • La diferencia es el tipo de norma. • L 1 es más general que L 2, conteniendo a este último. • Sin embargo, L 1 no tiene ningún tipo de producto interior razonable. • Por tanto no es el candidato que buscamos.

Un resumen de la convergencia. • Si la función es de cuadrado sumable, converge en norma. • Si la función y su derivada son continuas a trozos con un número finito de discontinuidades finitas, converge puntualmente y en norma. • Si f es continua con f(-pi)=f(pi) y la derivada es continua a trozos, converge uniformemente.

Resumen de la convergencia.

Formulación óptima. • L 2 proporciona alta calidad en la formulación. • Gracias a que una función está en L 2 si y sólo sí la suma parcial de Fourier que la aproxima converge en norma a la misma, así pues va a converger siempre • Esta expresión es muy parecida a una combinación lineal.

Formulación óptima. • Gracias a que en L 2 tenemos definido el producto interior, también tenemos la noción de ángulo y por tanto de ortogonalidad. • Sería interesante buscar una base de funciones ortogonal para aproximar una función en L 2. Entre estas bases tenemos: – Las exponenciales complejas. – Los sinusoides.

Formulación óptima. • Los coeficientes de la “combinación lineal” pueden obtenerse fácilmente mediante • La visualización geométrica es de gran ayuda.

Formulación óptima. • El conjunto de exponenciales complejas es orgonal: • La serie trigonométrica se obtiene:

La mejor aproximación. • Se demuestra que para una f en L 2, la suma parcial de Fourier da la mejor aproximación a dicha función en distancia cuadrática media. • Así pues, por ejemplo, la sinusoide de frecuencia “No” que mejor aproxima a una función de L 2 es

Maneras de ver L 2. • L 2 es la compleción de C(T) con respecto a la norma cuadrática media. Es decir, se trata del único espacio (salvo isomorfismos), métrico y completo que contiene a C(T) como subespacio denso. • L 2 es el espacio de funciones medibles 2 piperiódicas de cuadrado sumable, es decir, de señales de energía.

Maneras de ver L 2. • L 2 es el espacio de funciones 2 pi-periódicas tales que la suma parcial de Fourier converge en norma a f. • L 2 es un espacio de Hilbert complejo. • L 2 es isomorfo del espacio vectorial l 2(Z). • L 2 es el espacio de todas las funciones 2 pi-periódicas cuyas sucesiones de los coeficientes de Fourier son de cuadrado sumable. • L 2 es un espacio de funciones 2 pi-periódicas tales que f es una realización de la suma parcial de Fourier.