Thermal Properties of Materials Heat capacity specific heat

Thermal Properties of Materials Ø Heat capacity (specific heat) at constant volume Ø Heat capacity (specific heat) at constant pressure Ø Thermal conductivity (electrons, phonons) Ø Thermal expansion 1

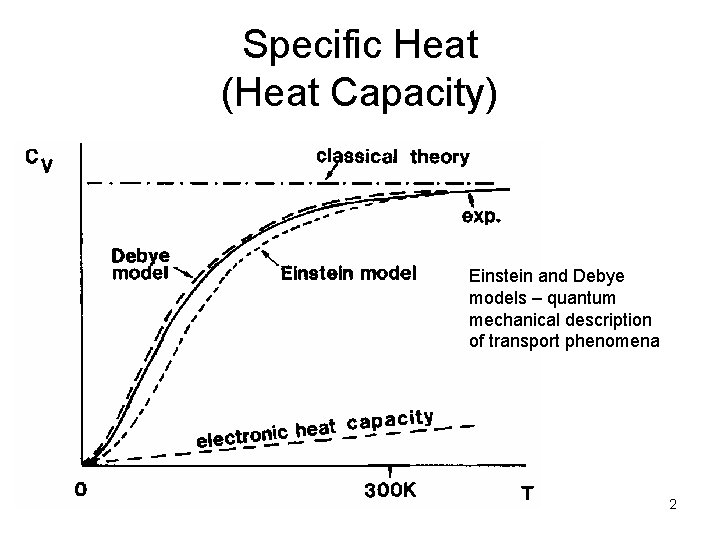
Specific Heat (Heat Capacity) Einstein and Debye models – quantum mechanical description of transport phenomena 2

Definition of the Heat Assumption, that: 3

Heat Capacity The amount of heat (energy) required to raise the systems temperature by one degree (usually expressed in Kelvin) 4

Specific Heat … per unit of mass: … per mole: Temperature dependency 5

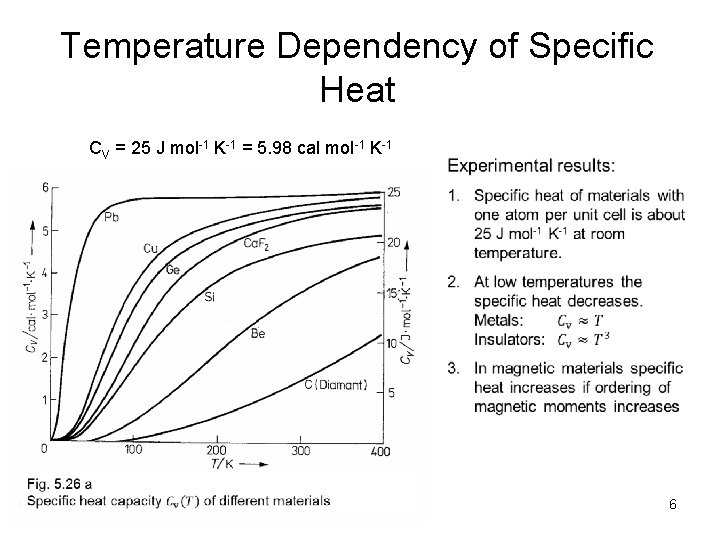
Temperature Dependency of Specific Heat CV = 25 J mol-1 K-1 = 5. 98 cal mol-1 K-1 6

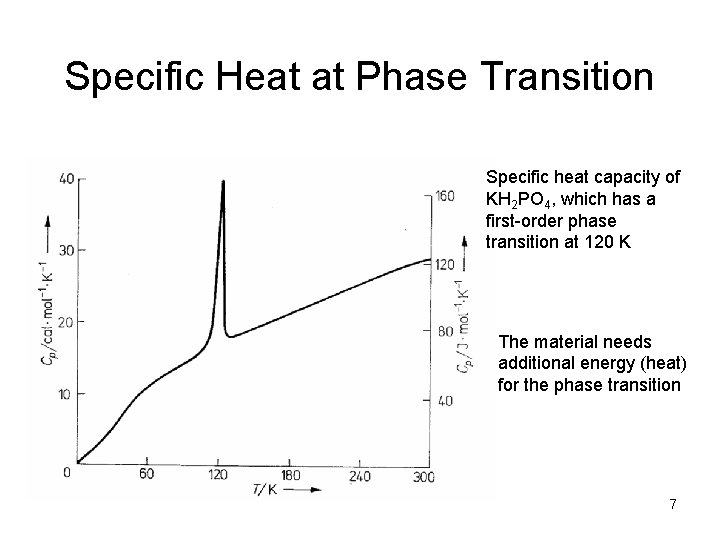
Specific Heat at Phase Transition Specific heat capacity of KH 2 PO 4, which has a first-order phase transition at 120 K The material needs additional energy (heat) for the phase transition 7

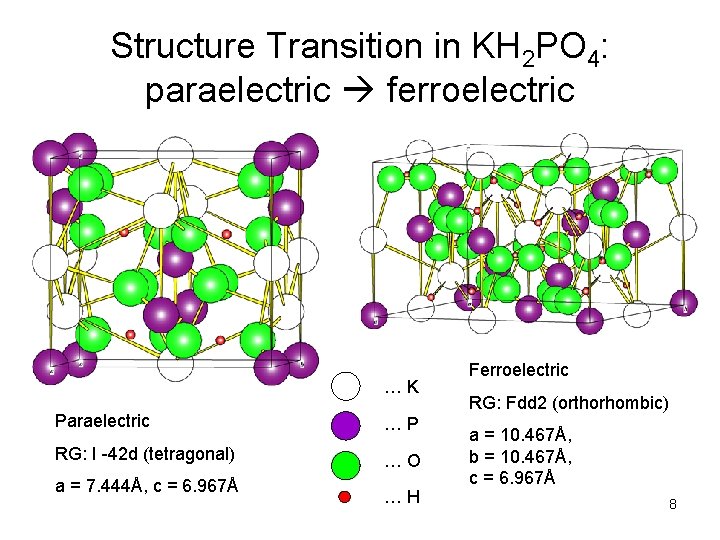
Structure Transition in KH 2 PO 4: paraelectric ferroelectric … K Paraelectric … P RG: I -42 d (tetragonal) … O a = 7. 444Å, c = 6. 967Å … H Ferroelectric RG: Fdd 2 (orthorhombic) a = 10. 467Å, b = 10. 467Å, c = 6. 967Å 8

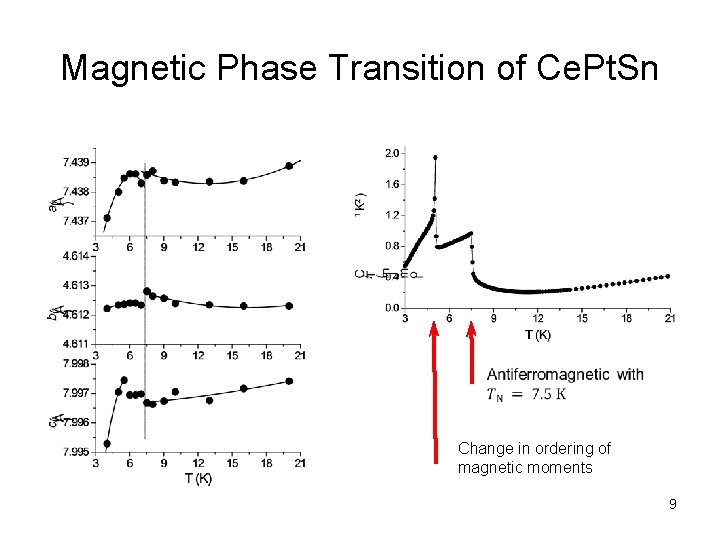
Magnetic Phase Transition of Ce. Pt. Sn Change in ordering of magnetic moments 9

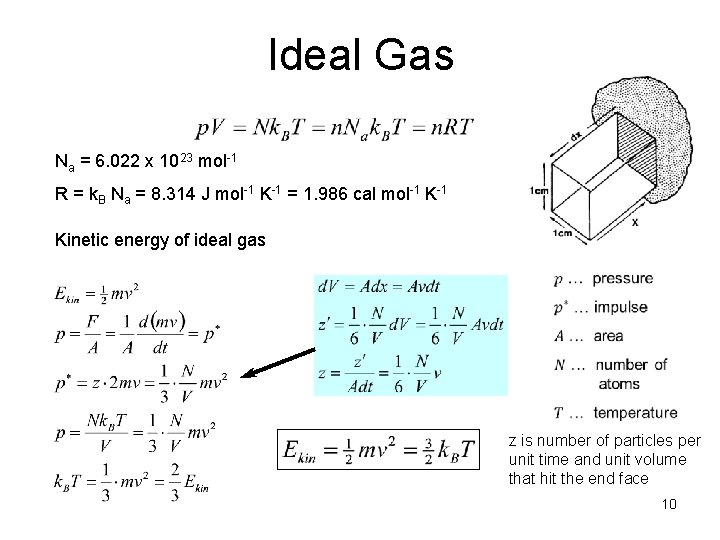
Ideal Gas Na = 6. 022 x 1023 mol-1 R = k. B Na = 8. 314 J mol-1 K-1 = 1. 986 cal mol-1 Kinetic energy of ideal gas z is number of particles per unit time and unit volume that hit the end face 10

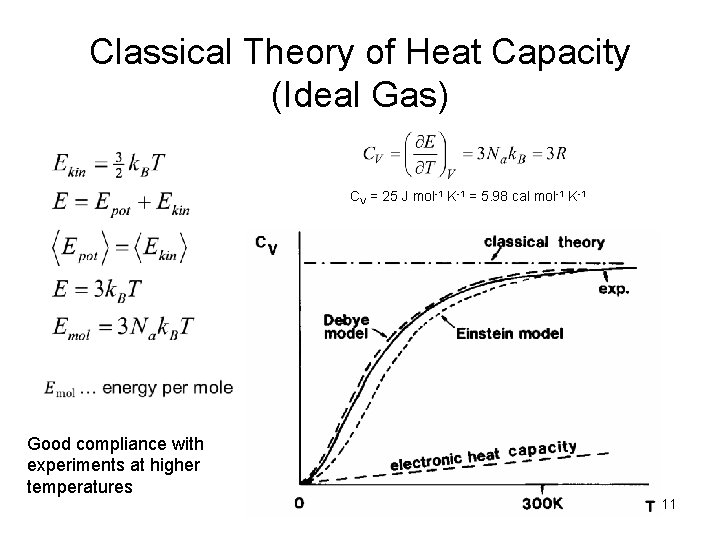
Classical Theory of Heat Capacity (Ideal Gas) CV = 25 J mol-1 K-1 = 5. 98 cal mol-1 K-1 Good compliance with experiments at higher temperatures 11

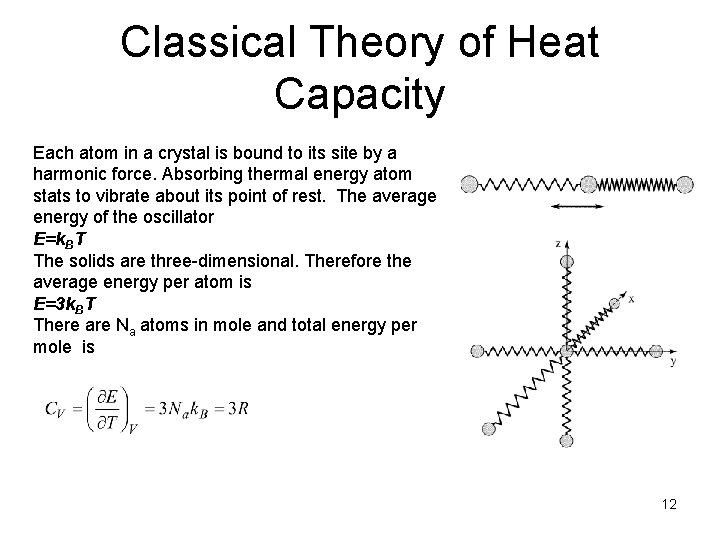
Classical Theory of Heat Capacity Each atom in a crystal is bound to its site by a harmonic force. Absorbing thermal energy atom stats to vibrate about its point of rest. The average energy of the oscillator E=k. BT The solids are three-dimensional. Therefore the average energy per atom is E=3 k. BT There are Na atoms in mole and total energy per mole is 12

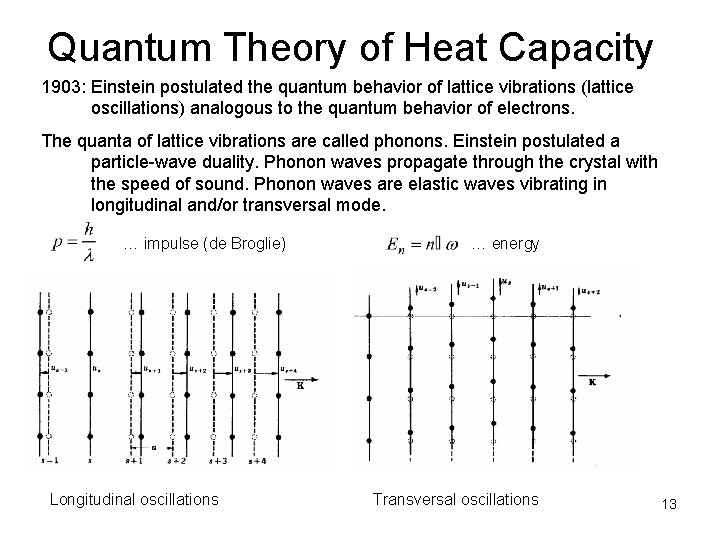
Quantum Theory of Heat Capacity 1903: Einstein postulated the quantum behavior of lattice vibrations (lattice oscillations) analogous to the quantum behavior of electrons. The quanta of lattice vibrations are called phonons. Einstein postulated a particle-wave duality. Phonon waves propagate through the crystal with the speed of sound. Phonon waves are elastic waves vibrating in longitudinal and/or transversal mode. … impulse (de Broglie) Longitudinal oscillations … energy Transversal oscillations 13

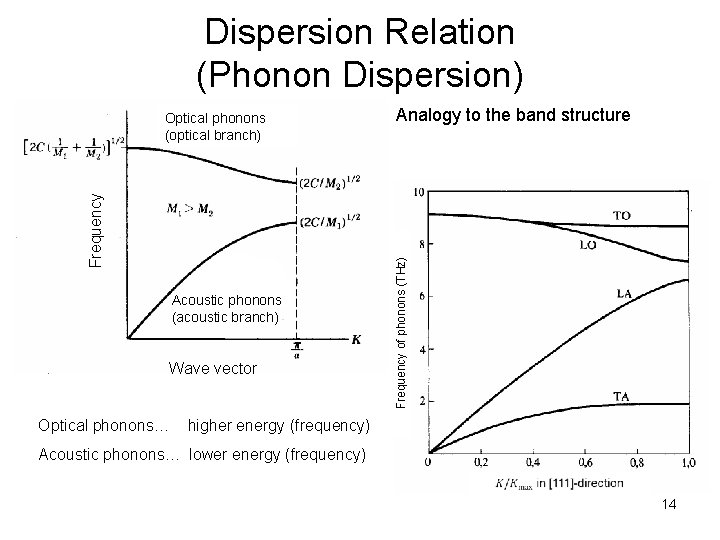
Dispersion Relation (Phonon Dispersion) Acoustic phonons (acoustic branch) Wave vector Analogy to the band structure Frequency of phonons (THz) Frequency Optical phonons (optical branch) Optical phonons… higher energy (frequency) Acoustic phonons… lower energy (frequency) 14

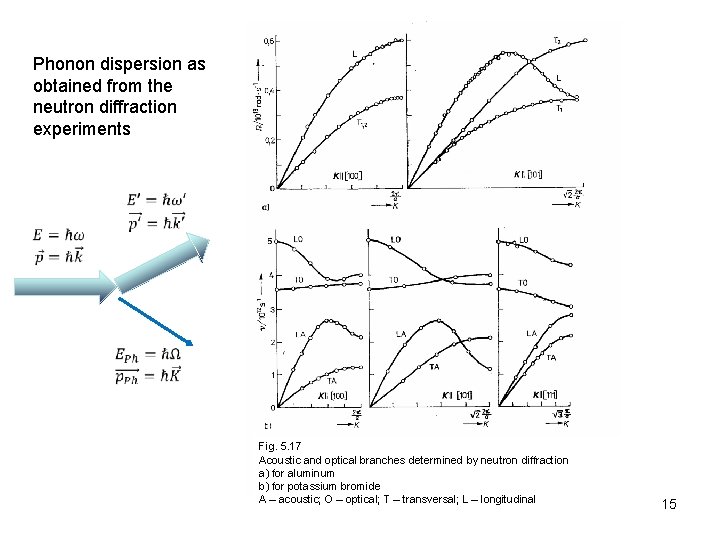
Phonon dispersion as obtained from the neutron diffraction experiments Fig. 5. 17 Acoustic and optical branches determined by neutron diffraction a) for aluminum b) for potassium bromide A – acoustic; O – optical; T – transversal; L – longitudinal 15

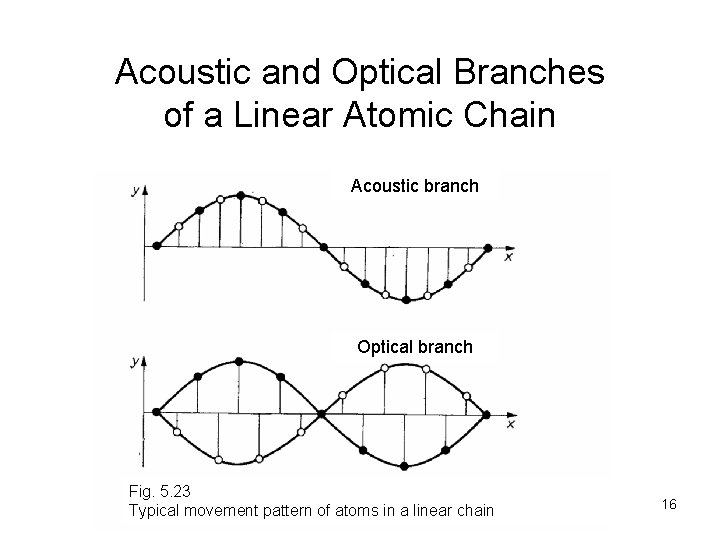
Acoustic and Optical Branches of a Linear Atomic Chain Acoustic branch Optical branch Fig. 5. 23 Typical movement pattern of atoms in a linear chain 16

Energy of a Quantum Mechanical Oscillator … quantum energies … Bose-Einstein distribution … Fermi function (distribution) of electrons 17

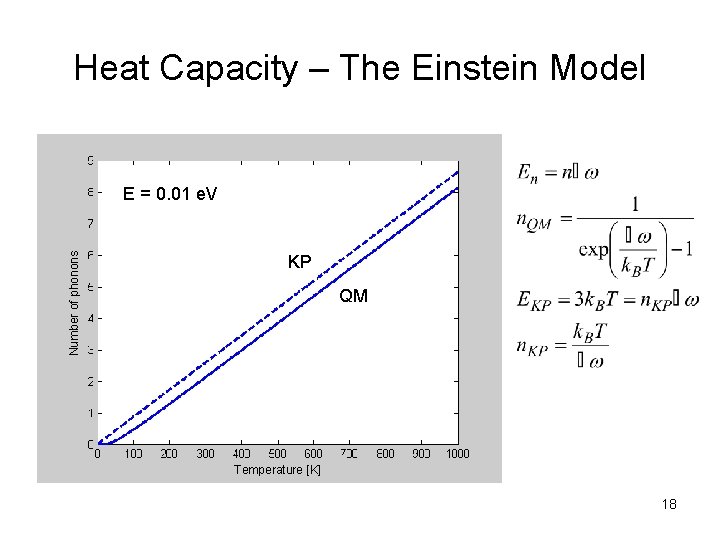
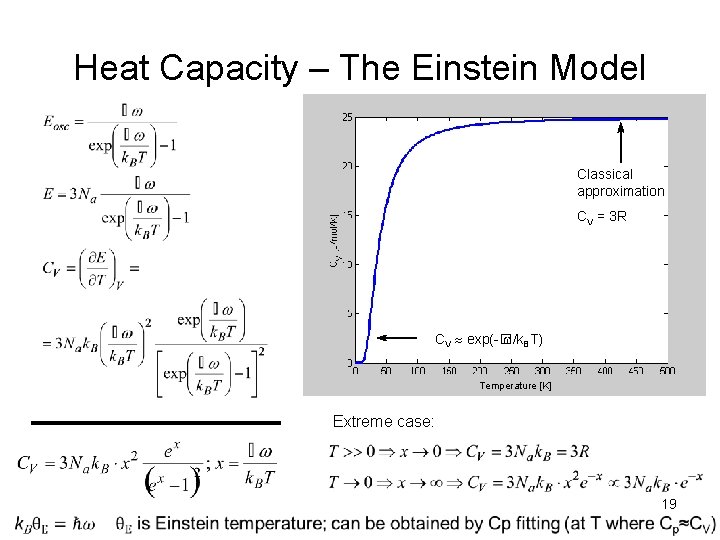
Heat Capacity – The Einstein Model Number of phonons E = 0. 01 e. V KP QM Temperature [K] 18

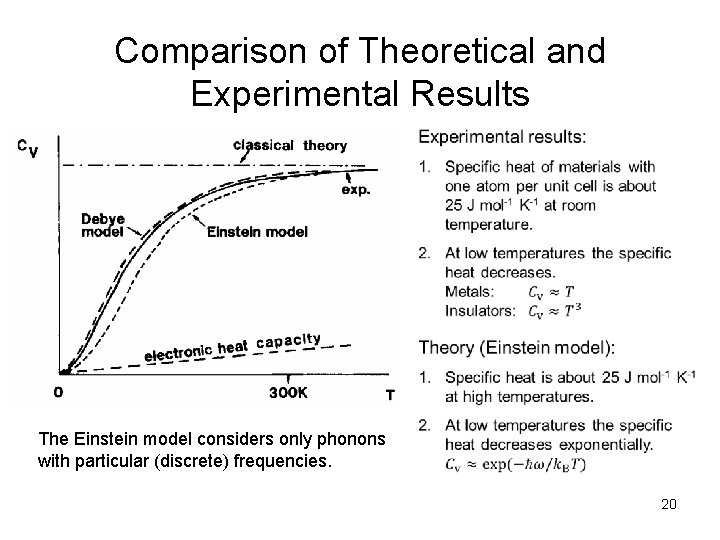
Heat Capacity – The Einstein Model Classical approximation CV = 3 R CV exp(-� /k. BT) Temperature [K] Extreme case: 19

Comparison of Theoretical and Experimental Results The Einstein model considers only phonons with particular (discrete) frequencies. 20

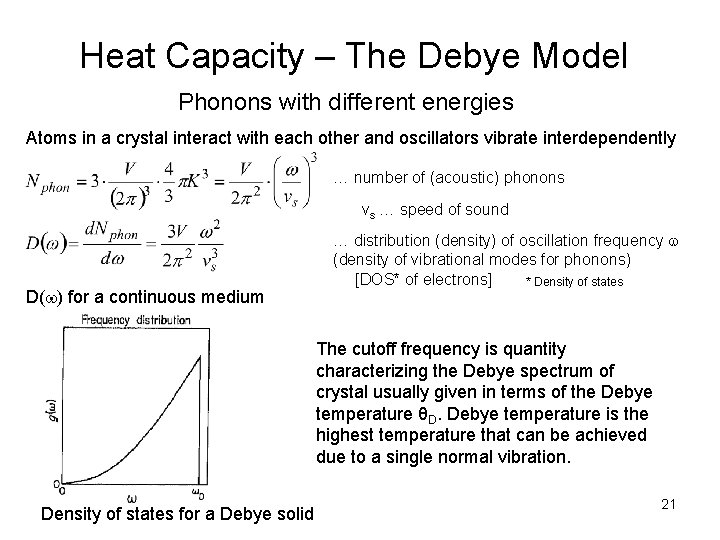
Heat Capacity – The Debye Model Phonons with different energies Atoms in a crystal interact with each other and oscillators vibrate interdependently … number of (acoustic) phonons vs … speed of sound D( ) for a continuous medium … distribution (density) of oscillation frequency (density of vibrational modes for phonons) [DOS* of electrons] * Density of states The cutoff frequency is quantity characterizing the Debye spectrum of crystal usually given in terms of the Debye temperature θD. Debye temperature is the highest temperature that can be achieved due to a single normal vibration. Density of states for a Debye solid 21

Heat Capacity – The Debye Model Debye modified Einstein equation by replacing 3 Na oscillators of single frequency with number of modes in a frequency interval d and by summing up over allowed frequencies. The total energy of vibration for solid is then Eosc is the same as in Einstein model 22

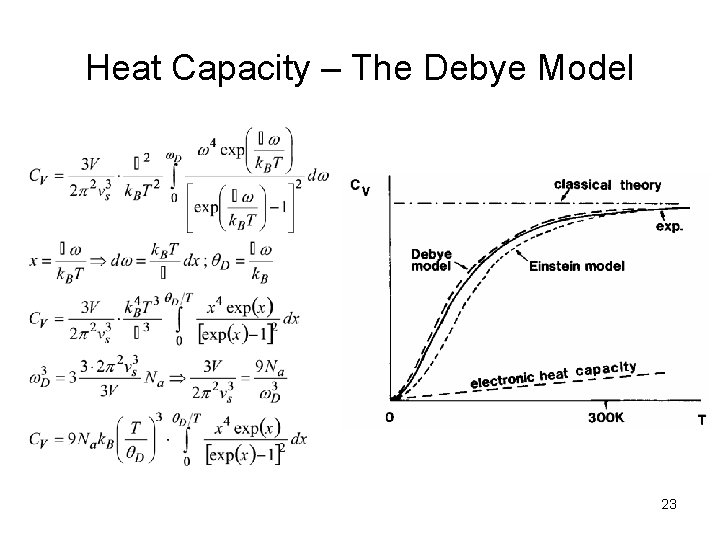
Heat Capacity – The Debye Model 23

Heat Capacity – The Debye Model Debye temperature – calculation from elastic constants The Debye model assumes that the solid is an elastic continuum in which all the sound waves travel at the same velocity independent of their wave length. Thus the phonon density of state becomes parabolic and Debye cutoff frequency, D, can be determined by normalization condition that the total number of frequencies should be equal the 3 N (N number of atoms). The Debye temperature is a measure of cutoff frequency and it is proportional to Debye sound velocity v. D: The v. D is independent of crystallographic directions, but different for the longitudinal and transverse branches L and S are longitudinal and transverse moduli Voigt-Reus-Hill approximation: n is Poisson ratio of polycrystalline material, B is bulk modulus 24

Heat Capacity – The Debye Model Poisson ratio is negative of the ratio of transverse strain to axial strain r 0 is equilibrium Wigner-Seitz radius defined as Alternative route is to calculate q. D is to fit measured Cp data is the low temperature range, where Cp≈CV using q. D as fitting parameters 25

Debye temperature – calculation from XRD Diffraction measurements provide two convenient methods to determine Debye temperature: in the first method the variation of Bragg intensity of a particular reflection (or reflections) with the temperature is measured, while in the second variation of Bragg intensity with reflection angle at fixed temperature is measured. The second method require a knowledge of theoretical atomic scattering factor. The measured structure factor F(hkl) is related to the atomic scattering factor f(hkl) by equation where B is Debye-Waller temperature factor and K is the conversion factor. In terms of the Debye theory B is given by where y (x) is Debye integral, q. M is Debye temperature appropriate to diffraction measurements. 26

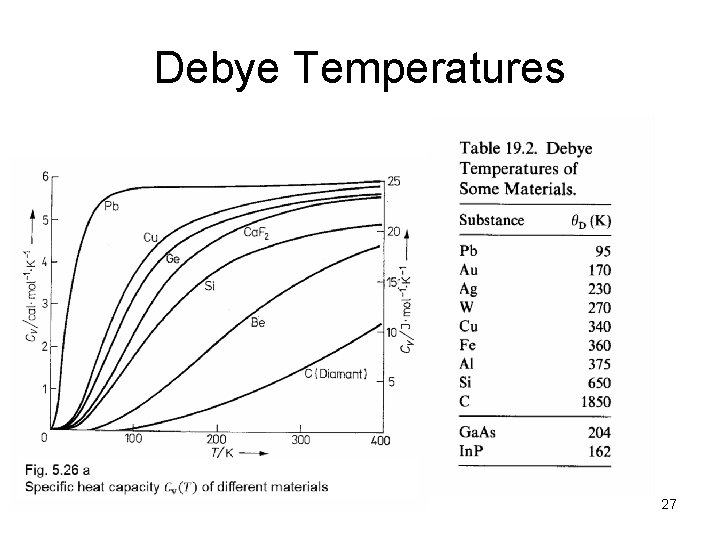
Debye Temperatures 27

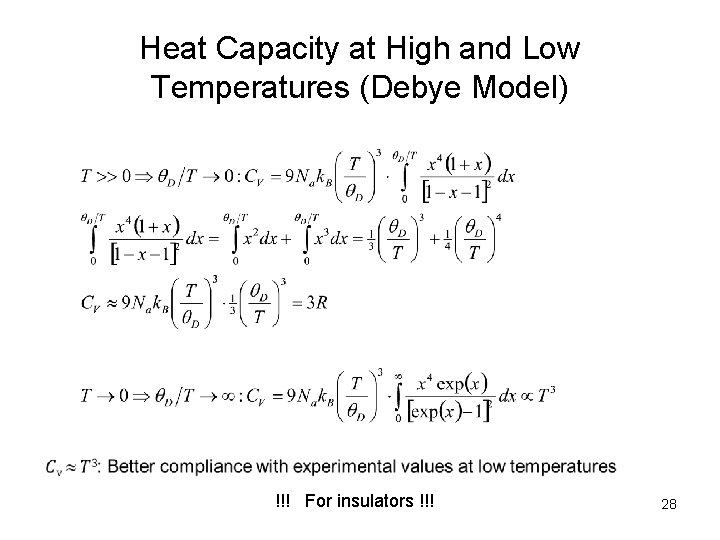
Heat Capacity at High and Low Temperatures (Debye Model) !!! For insulators !!! 28

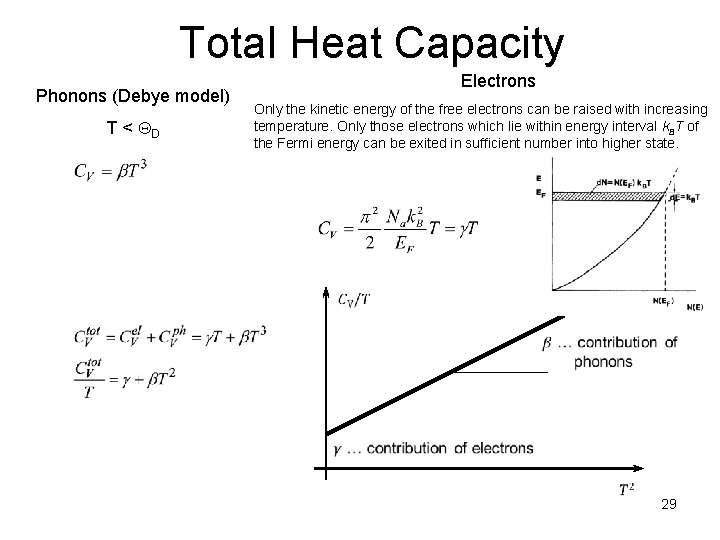
Total Heat Capacity Phonons (Debye model) T < QD Electrons Only the kinetic energy of the free electrons can be raised with increasing temperature. Only those electrons which lie within energy interval k. BT of the Fermi energy can be exited in sufficient number into higher state. 29

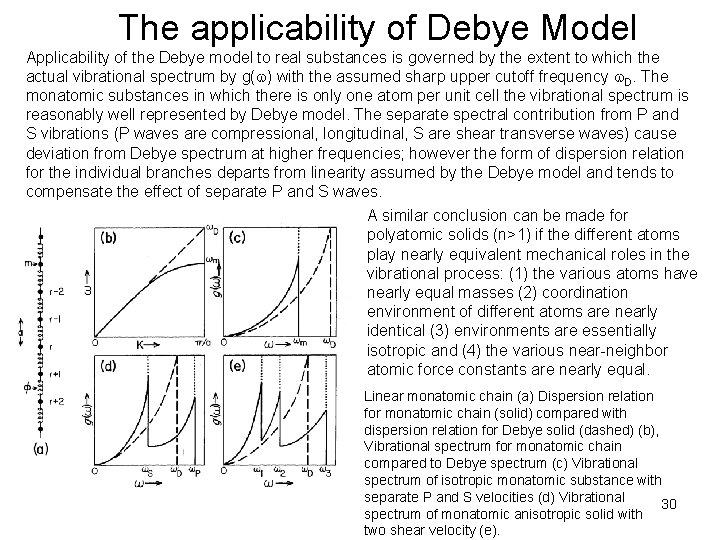
The applicability of Debye Model Applicability of the Debye model to real substances is governed by the extent to which the actual vibrational spectrum by g( ) with the assumed sharp upper cutoff frequency D. The monatomic substances in which there is only one atom per unit cell the vibrational spectrum is reasonably well represented by Debye model. The separate spectral contribution from P and S vibrations (P waves are compressional, longitudinal, S are shear transverse waves) cause deviation from Debye spectrum at higher frequencies; however the form of dispersion relation for the individual branches departs from linearity assumed by the Debye model and tends to compensate the effect of separate P and S waves. A similar conclusion can be made for polyatomic solids (n>1) if the different atoms play nearly equivalent mechanical roles in the vibrational process: (1) the various atoms have nearly equal masses (2) coordination environment of different atoms are nearly identical (3) environments are essentially isotropic and (4) the various near-neighbor atomic force constants are nearly equal. Linear monatomic chain (a) Dispersion relation for monatomic chain (solid) compared with dispersion relation for Debye solid (dashed) (b), Vibrational spectrum for monatomic chain compared to Debye spectrum (c) Vibrational spectrum of isotropic monatomic substance with separate P and S velocities (d) Vibrational 30 spectrum of monatomic anisotropic solid with two shear velocity (e).

Experimental Methods for the investigation of lattice vibrations X-ray diffraction Neutron diffraction Profile change of electron density (thermal vibrations of electrons) Interaction between low-energy (slow) neutrons and the Phonons Influence on the intensities of diffraction lines 31

Thermal Conductivity (Survey) Contribution to thermal conductivity: Ø Phonons (lattice vibrations) low contribution to thermal conductivity Ø Electrons (connected to electrical conductivity) high contribution to thermal conductivity 32

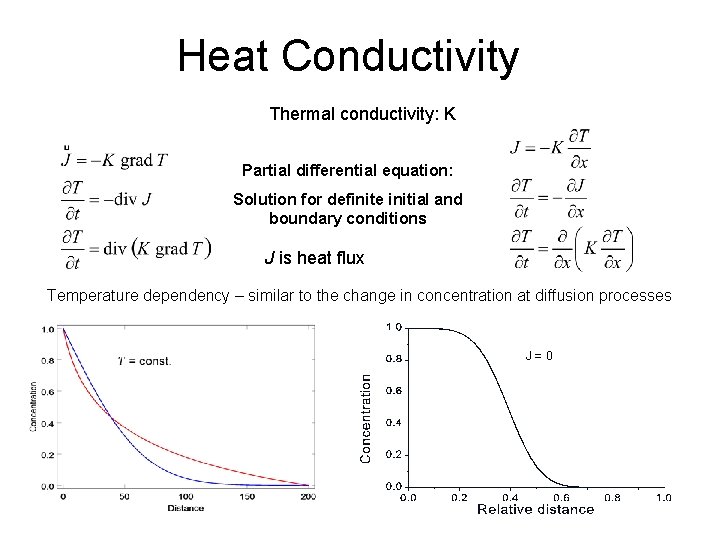
Heat Conductivity Thermal conductivity: K Partial differential equation: Solution for definite initial and boundary conditions J is heat flux Temperature dependency – similar to the change in concentration at diffusion processes J = 0 33

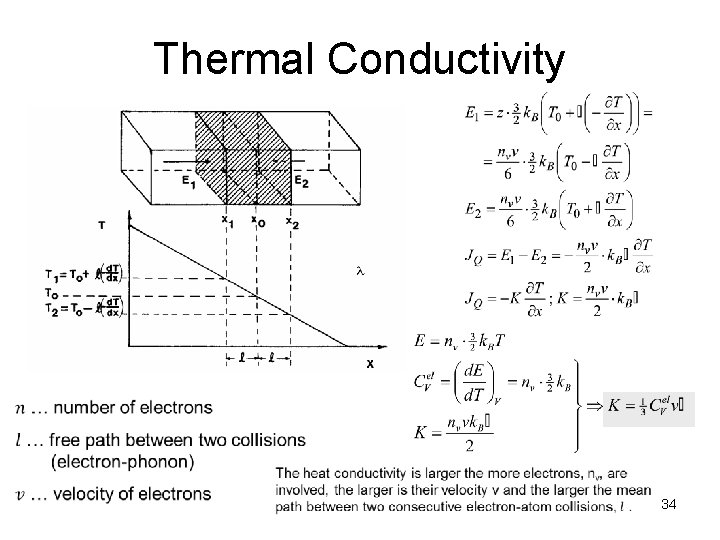
Thermal Conductivity 34

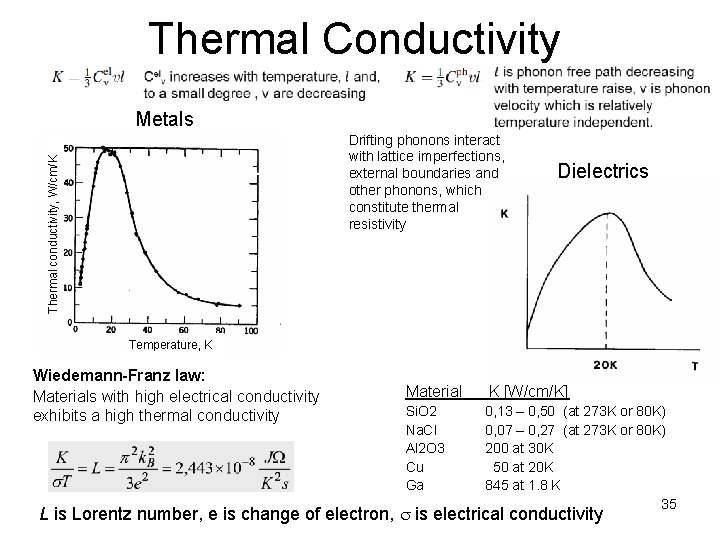
Thermal Conductivity Metals Thermal conductivity, W/cm/K Drifting phonons interact with lattice imperfections, external boundaries and other phonons, which constitute thermal resistivity Dielectrics Temperature, K Wiedemann-Franz law: Materials with high electrical conductivity exhibits a high thermal conductivity Material K [W/cm/K] Si. O 2 Na. Cl Al 2 O 3 Cu Ga 0, 13 – 0, 50 (at 273 K or 80 K) 0, 07 – 0, 27 (at 273 K or 80 K) 200 at 30 K 50 at 20 K 845 at 1. 8 K 35 L is Lorentz number, e is change of electron, s is electrical conductivity

Experimental methods to measure thermal conductivity Steady state and non-steady state methods Guarded hot plate. A solid sample is places between two plates: one is heated and the other is cooled. Temperature of plates is monitored until they are constant. The steady state temperatures, thickness of sample and heat input of hot plate are used to calculate thermal conductivity K q is quantity of heat passing through a unit area, distance between two sides of the sample T 1 and T 2 are temperatures on warmer side and lower side Hot wire and modified hot wire. The heated wire is inserted into material Laser flash diffusivity. A laser flash deliver short pulse of heat to the front of sample and infrared scanner observes the temperature change at the rare face as function of time. K=a(T) r(T) Cp(T), where a is thermal diffusivity [m 2 s-1], Cp is specific heat [J kg-1 K-1], r is density [kg m-3] 36

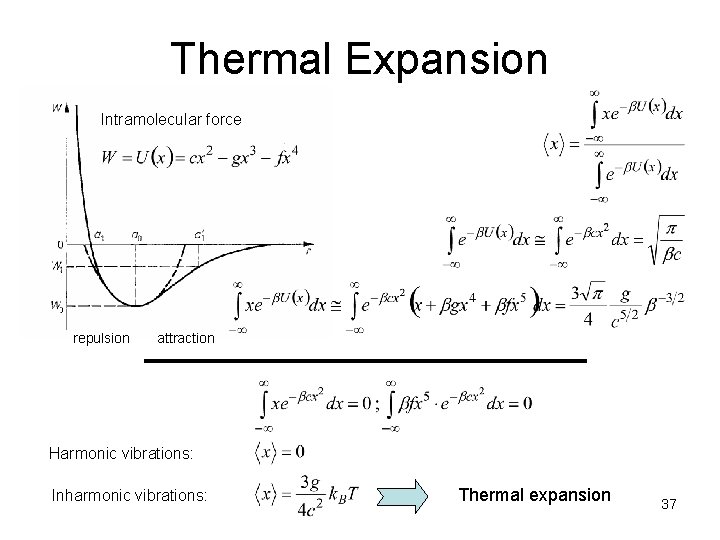
Thermal Expansion Intramolecular force repulsion attraction Harmonic vibrations: Inharmonic vibrations: Thermal expansion 37

Thermal Expansion Change of mean interatomic distance with temperature: Argon (kfz) Density [g/cm³] Lattice parameter [Å] Temperature dependency of lattice parameters: Temperature [K] 38

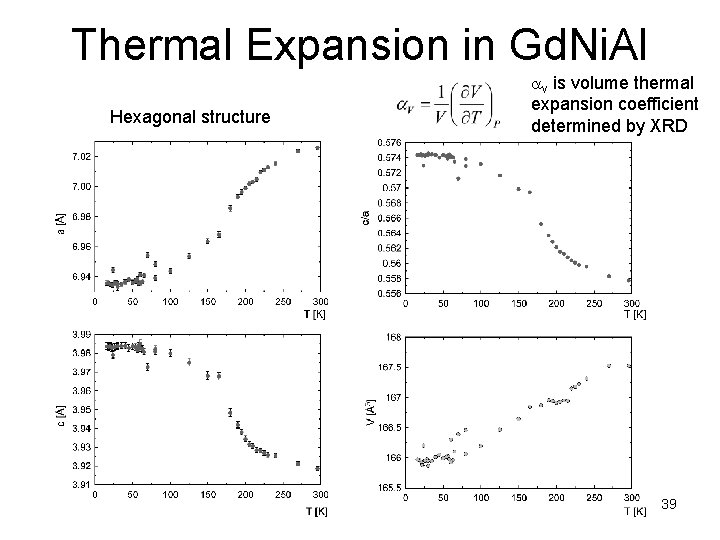
Thermal Expansion in Gd. Ni. Al Hexagonal structure av is volume thermal expansion coefficient determined by XRD 39

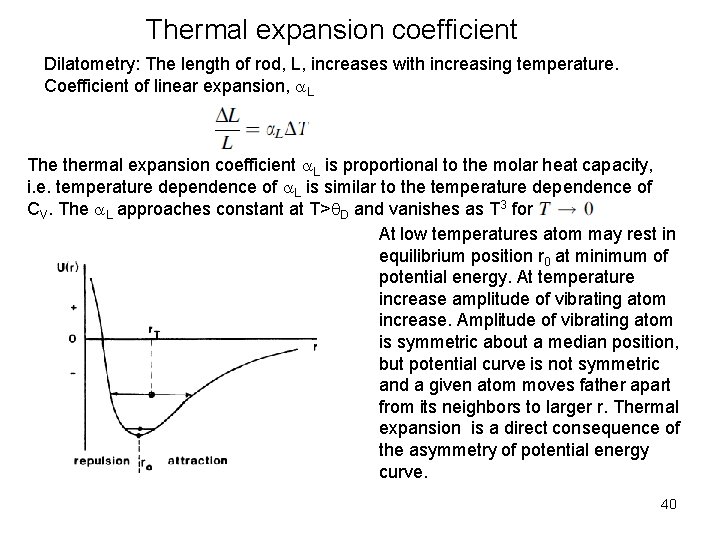
Thermal expansion coefficient Dilatometry: The length of rod, L, increases with increasing temperature. Coefficient of linear expansion, a. L The thermal expansion coefficient a. L is proportional to the molar heat capacity, i. e. temperature dependence of a. L is similar to the temperature dependence of CV. The a. L approaches constant at T>q. D and vanishes as T 3 for At low temperatures atom may rest in equilibrium position r 0 at minimum of potential energy. At temperature increase amplitude of vibrating atom increase. Amplitude of vibrating atom is symmetric about a median position, but potential curve is not symmetric and a given atom moves father apart from its neighbors to larger r. Thermal expansion is a direct consequence of the asymmetry of potential energy curve. 40