Specific heat of gases Specific heat of monatomic




















- Slides: 26

Specific heat of gases

Specific heat of monatomic gas I z. Add heat keeping the volume constant. Energy can only go into kinetic energy of atoms: z. Conclusion:

Specific heat of a monatomic gas II z. Add heat keeping the pressure constant. Energy can go into kinetic energy of atoms, or into work when the gas expands: z. Some mathematical gymnastics:

Specific heat of a monatomic gas III z. Substitute: z. Conclusion: z. Valid for all ideal gases

Equipartition of energy z. According to classical mechanics, molecules in thermal equilibrium have an average energy of associated with each independent degree of freedom of their motion provided that the expression for energy is quadratic. zmonatomic gas: x, y, z motion: since the terms are quadratic

Degrees of freedom for molecules z. We take m to be the mass of the molecule, then as for monatomic gases z. However, there is now internal energy due to rotation and vibration:

Diatomic molecule: rotation z. Think of molecule as dumbbell: z. Centre-of-mass (CM) moves with K. E. z. Rotation about CM with K. E. z. All quadratic: f = 6

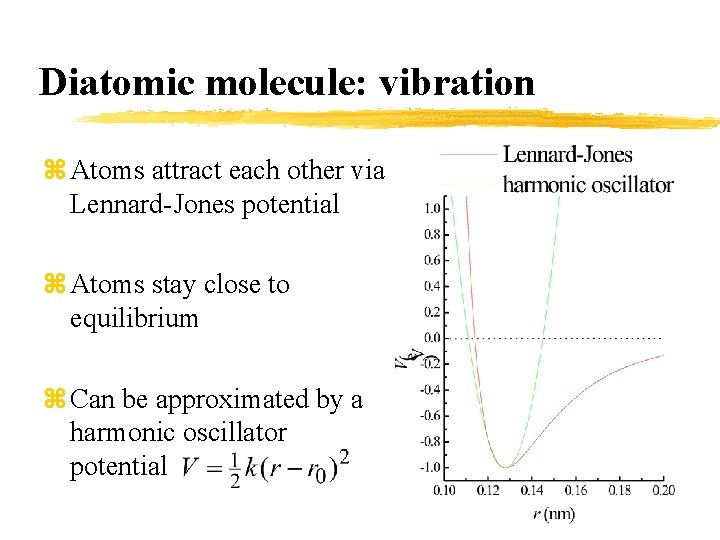
Diatomic molecule: vibration z Atoms attract each other via Lennard-Jones potential z Atoms stay close to equilibrium z Can be approximated by a harmonic oscillator potential

Harmonic oscillator z. Average P. E. = average K. E. z. P. E. associated with it is quadratic so z. K. E. is the same so also z. Total: k. T or f = 2.

Diatomic molecules: conclusion? z. According to classical physics there should be 8 degrees of freedom for each diatomic molecule… z. From Cp and CV measurements for H 2: ybelow 70 K: f = 3 yat room temperature: f = 5 yabove 5000 K: f = 7

Question z. If e. g. vibration of H 2 does not contribute to the specific heat, then that is because a) The vibration is independent of temperature b) The vibration doesn’t change in collisions c) The vibration is like a very stiff spring

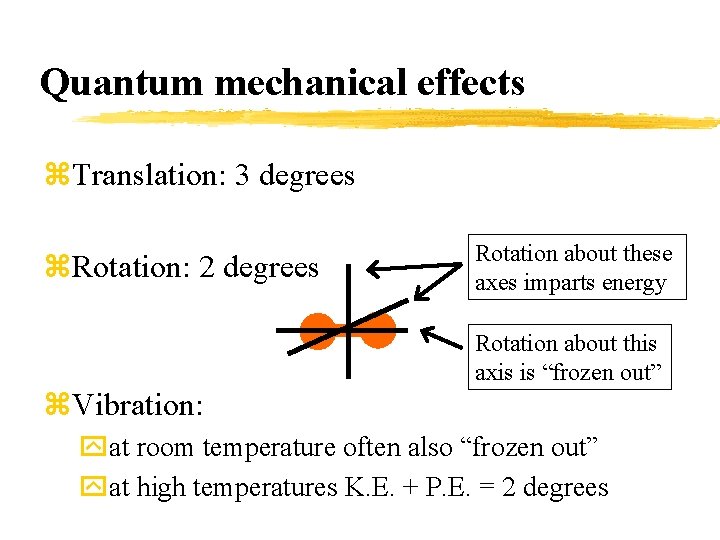
Quantum mechanical effects z. Translation: 3 degrees z. Rotation: 2 degrees Rotation about these axes imparts energy Rotation about this axis is “frozen out” z. Vibration: yat room temperature often also “frozen out” yat high temperatures K. E. + P. E. = 2 degrees

Rotational states z Quantum mechanics: rotational and vibrational energies not continuous but quantised z Rotation: spacing ~1/I ysmall steps, near-continuous about two axes ybig steps about axis through atoms y. If step >> k. T : not excited, no rotation y. Even at T=104 K no rotation about third axis

Vibrational states z Vibration: harmonic oscillator y. Spacing ~1/ m ystep >> k. T for light molecules (O 2, N 2) but excitations possible for heavy molecules such as I 2 y. Potential energy: on average equal to kinetic energy yvibration contributes k. T when it does

Solids z. Model for solid: z. Elemental (“monatomic”) solids have K. E. and P. E. to give C = 3 R (Rule of Dulong and Petit)

Freezing out - again z. At lower temperatures, some vibrational levels cannot be reached with k. T energy. At very low temperatures C T 3. z. For metals the electrons (which can move freely through the metal) contribute and = a. T + b. T 3 (Einstein-Debye model) C

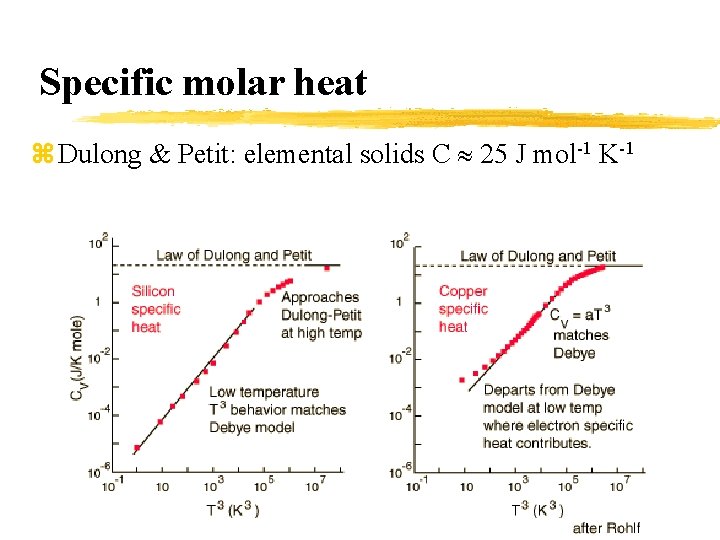
Specific molar heat z Dulong & Petit: elemental solids C 25 J mol-1 K-1

Question 2 z. A room measures 4. 00 2. 40 m 3. Assume the “air molecules” all have a velocity of 360 ms-1 and a mass of 5 10 -26 kg. The density of air is about 1 kg m-3. Calculate the pressure in this room.

Isothermal expansion of an ideal gas z. Isothermal expansion: pressure drops as volume increases since p. V = n. RT = constant z. The internal energy only depends on the temperature so it doesn’t change z. Two equations hold at the same time: p. V = n. RT and T 2 = T 1

Question z. An identical volume of the same gas expands adiabatically to the same volume. The pressure drops a) more than in the isothermal process b) by the same amount c) less than in the isothermal process

Adiabatic expansion of an ideal gas I z. Q = 0 so U + W = 0 z Remember: U = n. CV T z. Use ideal gas law: z. Substitute:

Adiabatic expansion of an ideal gas II z. Divide by n. CV T: z. Prepare for integration: z. Define so that

Adiabatic expansion of an ideal gas III z. Integrate: z. Play around with it: z. Use

Question z. Consider isothermal and adiabatic expansion of a Van der Waals gas. Do T 2 = T 1 and p. Vg = C hold for this gas? a) yes; yes b) yes; no c) no; yes d) no; no

Question z. A gas is compressed adiabatically. The temperature a) rises because work is done on the gas b) rises depending on how much heat is added c) drops because work is done by the gas d) drops depending on how much heat is added

PS 225 – Thermal Physics topics z. The atomic hypothesis z. Heat and heat transfer z. Kinetic theory z. The Boltzmann factor z. The First Law of Thermodynamics z. Specific Heat z. Entropy z. Heat engines z. Phase transitions
 Specific heat for monatomic gas
Specific heat for monatomic gas Constant specific heats
Constant specific heats Specific heat capacity of lead j/kg c
Specific heat capacity of lead j/kg c Latent heat dimension
Latent heat dimension Heat capacity ratio of gases lab report
Heat capacity ratio of gases lab report Monatomic ion periodic table
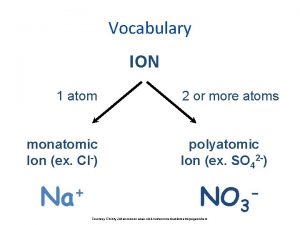
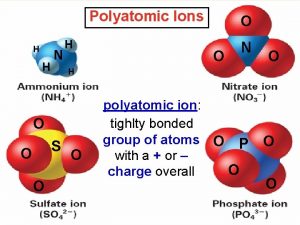
Monatomic ion periodic table Polyatomic ions
Polyatomic ions Monatomic and polyatomic ions
Monatomic and polyatomic ions Sulfur readily forms the following monatomic ion:
Sulfur readily forms the following monatomic ion: Monoatomic ions
Monoatomic ions Quantization of elastic waves
Quantization of elastic waves Monatomic ion definition chemistry
Monatomic ion definition chemistry Pf3 name of compound
Pf3 name of compound Monatomic formula
Monatomic formula Naming monatomic ions
Naming monatomic ions Mono atomic elements
Mono atomic elements Poly atomic ions
Poly atomic ions W=p(vf-vi)
W=p(vf-vi) Ionic bond and metallic bond
Ionic bond and metallic bond Specific weight
Specific weight Glycerol specific gravity
Glycerol specific gravity Specific heat of water
Specific heat of water Parerea tq mc
Parerea tq mc Specific heat of platinum
Specific heat of platinum Specific heat capacity of cheese
Specific heat capacity of cheese Difference between heat and thermal energy
Difference between heat and thermal energy Thermochemistry vocabulary
Thermochemistry vocabulary