Calculating specific heat capacities Calculating the specific heat




- Slides: 12

Calculating specific heat capacities

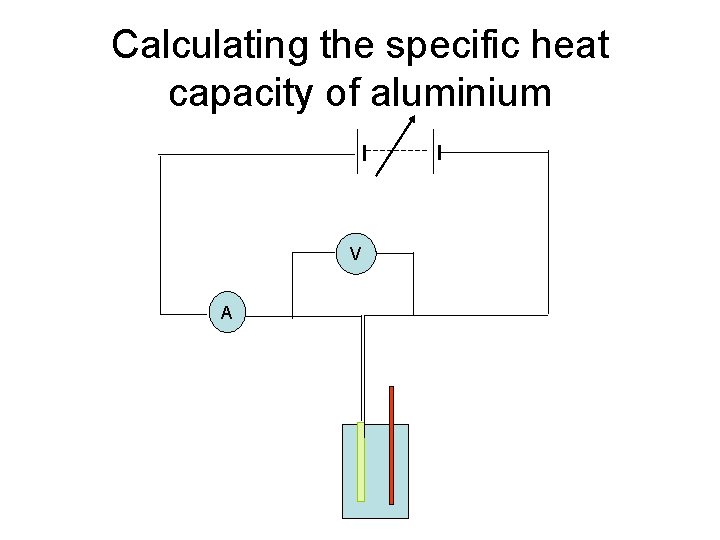
Calculating the specific heat capacity of aluminium V A

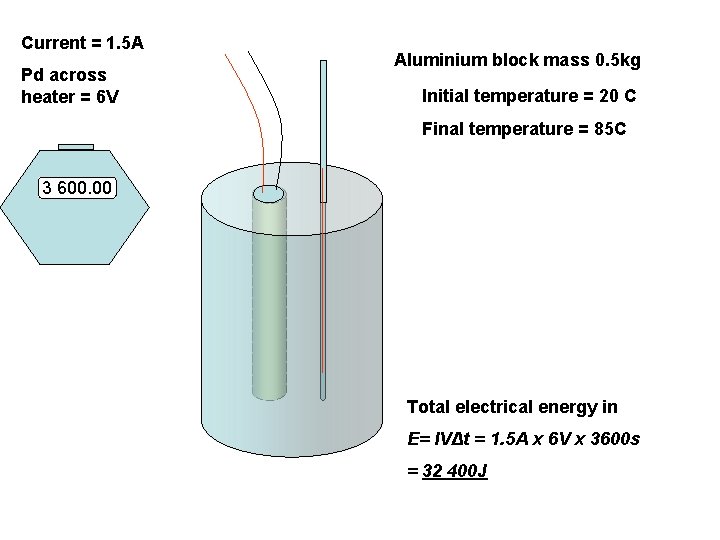
Current = 1. 5 A Pd across heater = 6 V Aluminium block mass 0. 5 kg Initial temperature = 20 C Final temperature = 85 C 3 600. 00 Total electrical energy in E= IVΔt = 1. 5 A x 6 V x 3600 s = 32 400 J

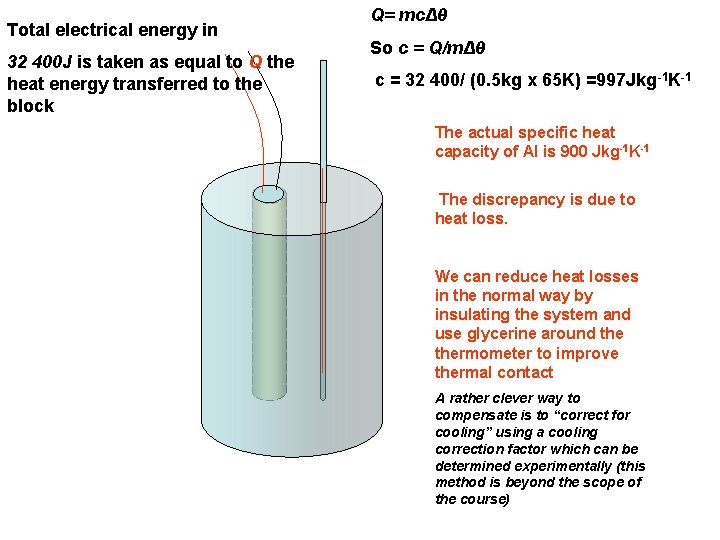
Total electrical energy in 32 400 J is taken as equal to Q the heat energy transferred to the block Q= mcΔθ So c = Q/mΔθ c = 32 400/ (0. 5 kg x 65 K) =997 Jkg-1 K-1 The actual specific heat capacity of Al is 900 Jkg-1 K-1 The discrepancy is due to heat loss. We can reduce heat losses in the normal way by insulating the system and use glycerine around thermometer to improve thermal contact A rather clever way to compensate is to “correct for cooling” using a cooling correction factor which can be determined experimentally (this method is beyond the scope of the course)

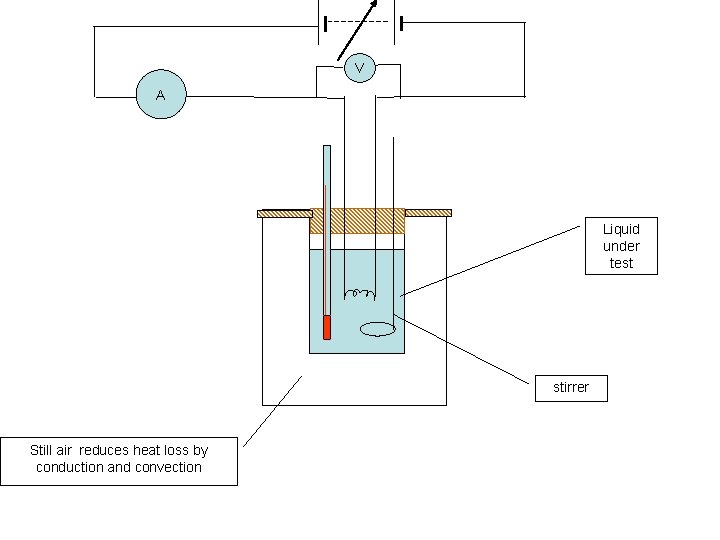
V A Liquid under test stirrer Still air reduces heat loss by conduction and convection

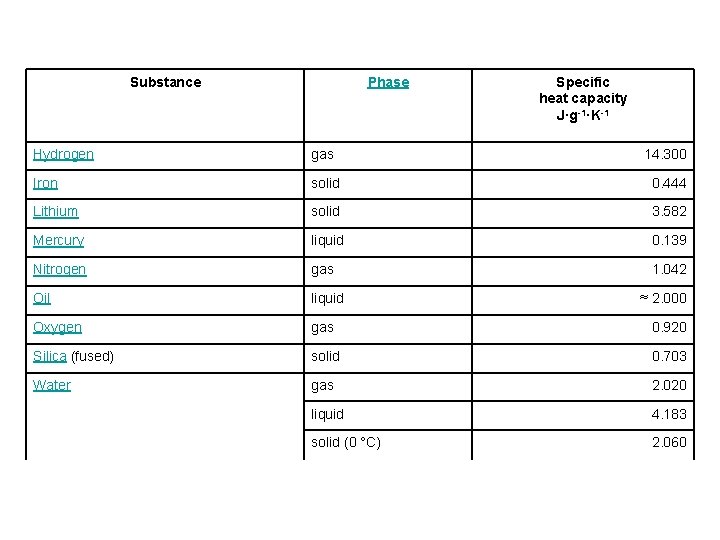
Substance Phase Specific heat capacity J·g-1·K-1 Hydrogen gas 14. 300 Iron solid 0. 444 Lithium solid 3. 582 Mercury liquid 0. 139 Nitrogen gas 1. 042 Oil liquid Oxygen gas 0. 920 Silica (fused) solid 0. 703 Water gas 2. 020 liquid 4. 183 solid (0 °C) 2. 060 ≈ 2. 000

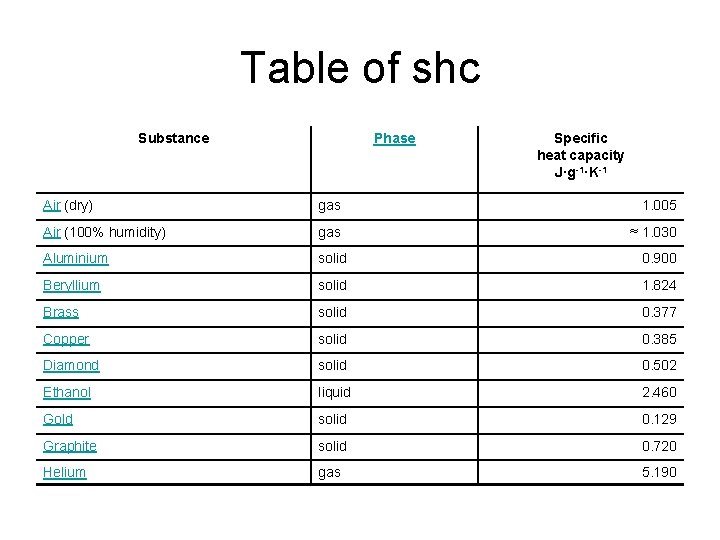
Table of shc Substance Phase Specific heat capacity J·g-1·K-1 Air (dry) gas 1. 005 Air (100% humidity) gas ≈ 1. 030 Aluminium solid 0. 900 Beryllium solid 1. 824 Brass solid 0. 377 Copper solid 0. 385 Diamond solid 0. 502 Ethanol liquid 2. 460 Gold solid 0. 129 Graphite solid 0. 720 Helium gas 5. 190

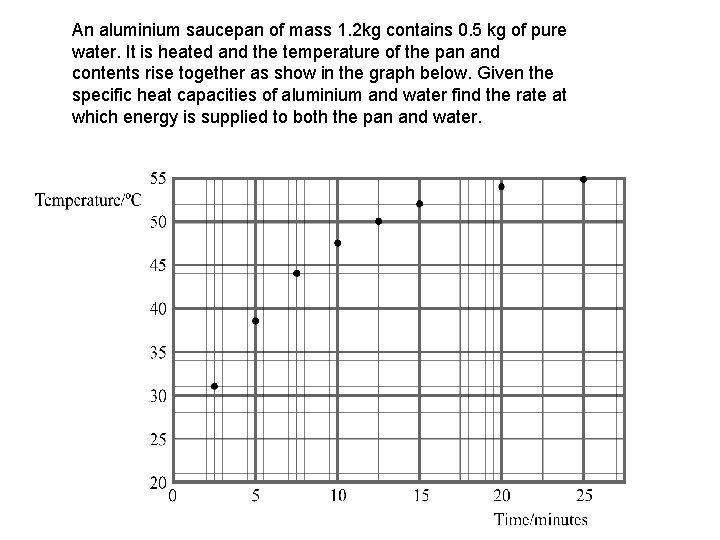
An aluminium saucepan of mass 1. 2 kg contains 0. 5 kg of pure water. It is heated and the temperature of the pan and contents rise together as show in the graph below. Given the specific heat capacities of aluminium and water find the rate at which energy is supplied to both the pan and water.

Aluminium has a specific heat capacity of 900 Jkg-1 K-1 Water has a specific heat capacity of 4 200 Jkg-1 K-1

This aluminium saucepan has a mass of 1. 2 kg Its heat capacity is 1. 2 x 900 = 1080 JK-1 The water in it has a mass of 0. 5 kg The heat capacity of this mass of water is 0. 5 x 4200 = 2100 JK-1 So the total heat capacity of the aluminium and the water is 1080 + 2100 = 3180 JK-1

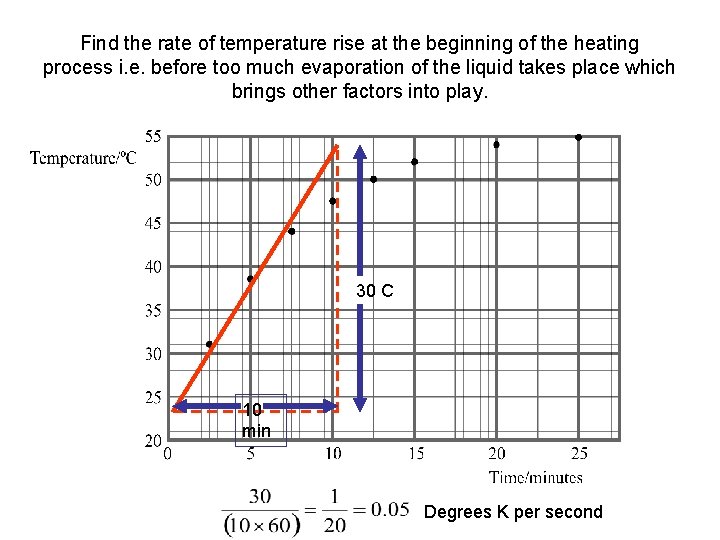
Find the rate of temperature rise at the beginning of the heating process i. e. before too much evaporation of the liquid takes place which brings other factors into play. 30 C 10 min Degrees K per second

For the pan and water together Heat capacity = 3180 JK-1 Temperature rise = 0. 05 Ks-1 Rate of energy change = Heat capacity x rate of temperature rise P. S. If you are doing this you should get around 230 W as the gradient of the graph that I have drawn is slightly different from that given in the question